风载荷作用下V形绝缘子串的力学特性分析

2021-03-22秦瑞江芮晓明

工程设计学报 2021年1期

周超，秦瑞江，芮晓明

（华北电力大学能源动力与机械工程学院，北京102206）

近年来，随着我国经济水平的稳步提升，工业生产和建设对电力的需求日益增加。然而，由于电力资源分布不均匀，有必要构建合理的电力网络以合理分配电力资源［1］。在输电塔线体系受到横向风载荷作用时，导线的摆动使得其与杆塔或其他周围事物的电气间隙减小。若电气间隙小于线路允许安全距离时，有可能发生击穿放电，进而导致跳闸事故，这一现象被称为风偏放电跳闸［2］。由线路故障的调查数据可知，风偏放电跳闸是造成线路故障的主要原因之一，已经对国家电力系统的安全造成了很大的影响，给人们的生产、生活造成了巨大的经济损失［3-4］。随着电压等级的不断提升，绝缘子串的抗风偏设计及防护亟须修正。风载荷及其他环境载荷对绝缘子串和整个输电线路的影响将愈加明显，因此，对绝缘子串在风载荷作用下的力学特性进行分析具有重要的工程意义。

国内外学者对输电线路风偏事故进行了大量分析，提出了相关绝缘子串的设计、改造措施。赵全江等［5-7］对Ⅴ形绝缘子串（以下简称为“Ⅴ串”）的力学模型进行简化，讨论了Ⅴ串的结构特征及其对输电塔的载荷作用，进一步了分析了Ⅴ串风偏角对输电塔线体系整体稳定性的影响。黄立新等［8-9］通过相关的试验，分别对复合绝缘子和陶瓷绝缘子的受力特征进行分析，并讨论了绝缘子串背风侧的变形和应力变化。Kumoso等［10-11］利用有限元软件建立了复合绝缘子芯棒模型，对其施加轴向拉力并分析其受力特点。蔡林峰等［12］研究了不同类型绝缘子串的力学特性，并对复合绝缘子芯棒展开了详细的屈曲分析。然而，由于输电塔线体系风偏振动问题的复杂性，许多相关问题至今没有得到有效解决。

本文以我国云南地区某山区典型的架空线路为研究对象，基于ANSYS有限元仿真软件对不同Ⅴ串的受力特性进行研究。首先，对Ⅴ串在水平风载荷作用下的受力情况进行理论分析；其次，对复合绝缘子串芯棒进行各向同性、各向异性特征值屈曲分析，以验证模型的正确性，并分析芯棒发生屈曲变形的主要影响因素；最后，对比分析双联及四联Ⅴ串在风载荷作用下的力学特性，对其迎风侧和背风侧的变形、所受最大应力及其最低点水平位移的变化规律进行研究，从而为Ⅴ串的设计改进提供有价值的参考依据。

1 V形绝缘子串的受力分析

以我国云南地区某山区的500 kⅤ小和线为研究对象。N46杆塔参数如表1所示，N46杆塔断面如图1所示，N46杆塔塔头绝缘子布置如图2所示。

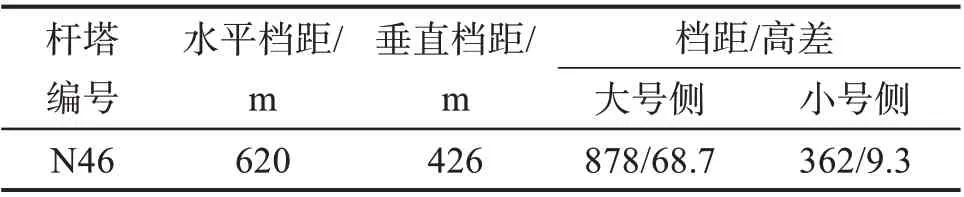
表1 N46杆塔参数Table 1 N46 tower parameters

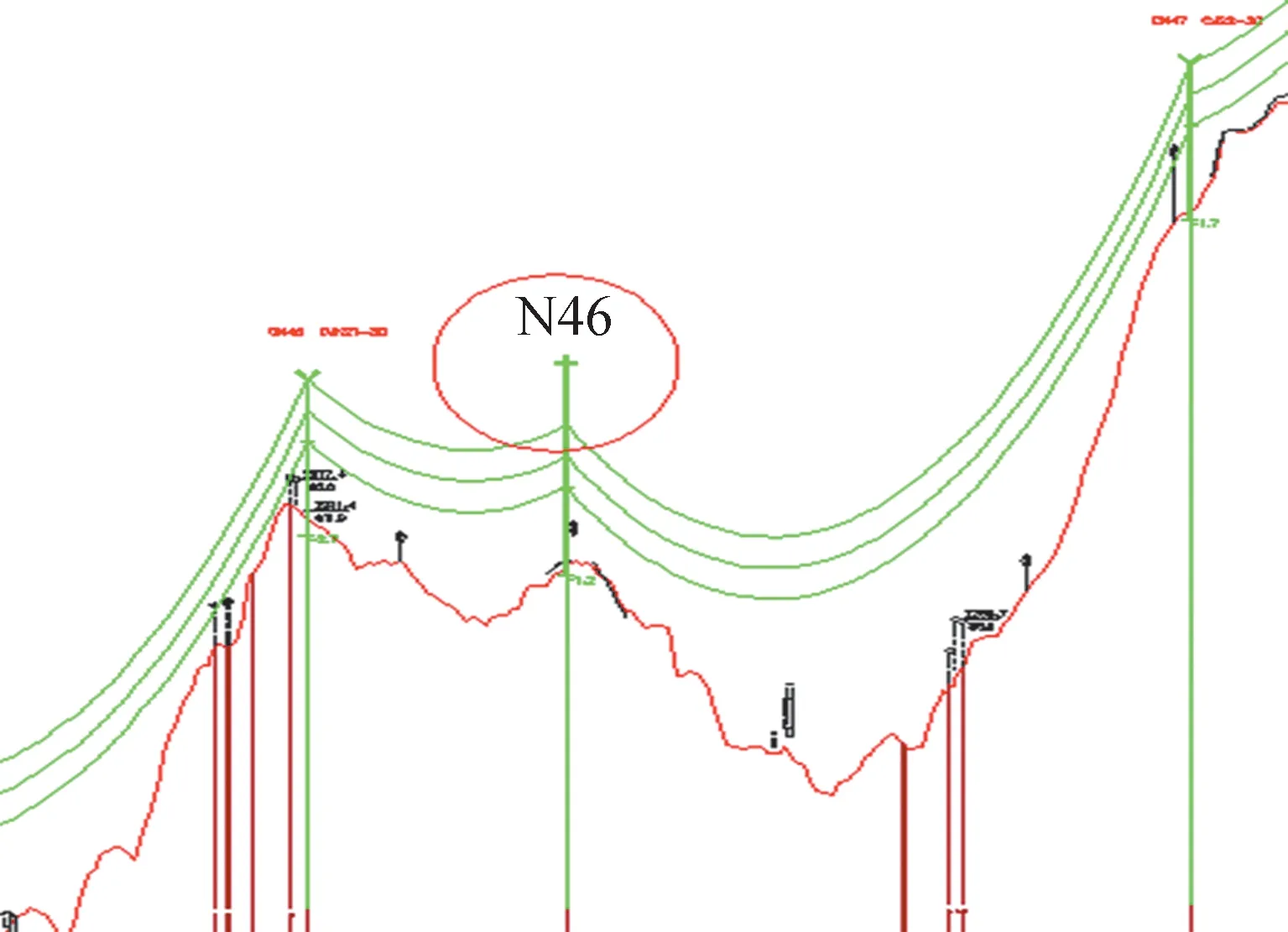
图1 N46杆塔断面示意Fig.1 Sectional view of N46 tower

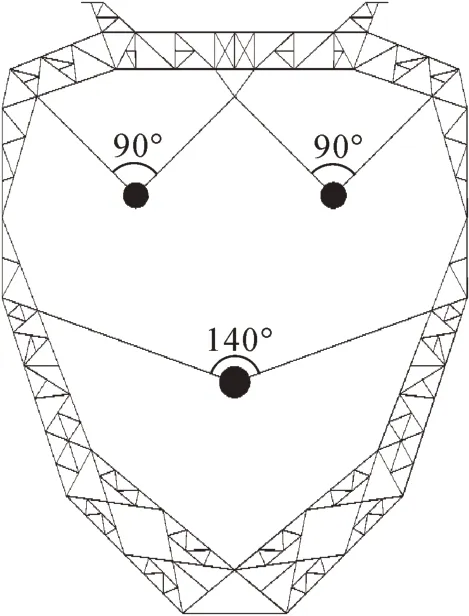
图2 N46杆塔塔头绝缘子布置示意Fig.2 Schematic of insulator layout of N46 tower head

500 kⅤ小和线N43 至N49 杆塔的海拔高度为2 230～2 306 m，N46杆塔位于山顶鞍部。N43至N49杆塔的线路呈东西走向，呈西低东高之势。该山区呈强烈侵蚀深切峡谷地貌，西边有两大峡谷，属典型的微地形、微气象区，且N46杆塔处在垭口，易发生大风灾害。该段线路的导线为6×LGJ-300/40钢芯铝绞线，其参数如表2所示。架空地线分别为LBGJ80-20AC和OPGW 光缆。Ⅴ串型号为FXBW-500/300SCⅠ，其参数如表3所示。

为了改善绝缘子串受力以及减弱导线振动，也为了减小整体输电塔塔头的尺寸，Ⅴ串应运而生。由于风力作用，导线、绝缘子串及其相关金具会受到横向载荷作用，在沿风向作加速运动。将绝缘子串在N46等紧凑型杆塔中呈Ⅴ形安装，能够很好地限制绝缘子及金具的水平运动。Ⅴ串的受力与普通的绝缘子串有很大的差异：面向风载荷一侧的绝缘子联会承受极大的拉力，背向风载荷一侧的绝缘子联承受的拉力会逐渐减小，并逐渐由拉力转化为压力。如图3所示，该Ⅴ串承受的外力包括导线、绝缘子金具等自重载荷Gv和风载荷Ph，其合力为P，2 条绝缘子串承受的拉应力、压应力分别为F1和F2。

表2 LGJ-300/40钢芯铝绞线参数Table 2 Parameters of LGJ-300/40 steel core aluminum stranded wire

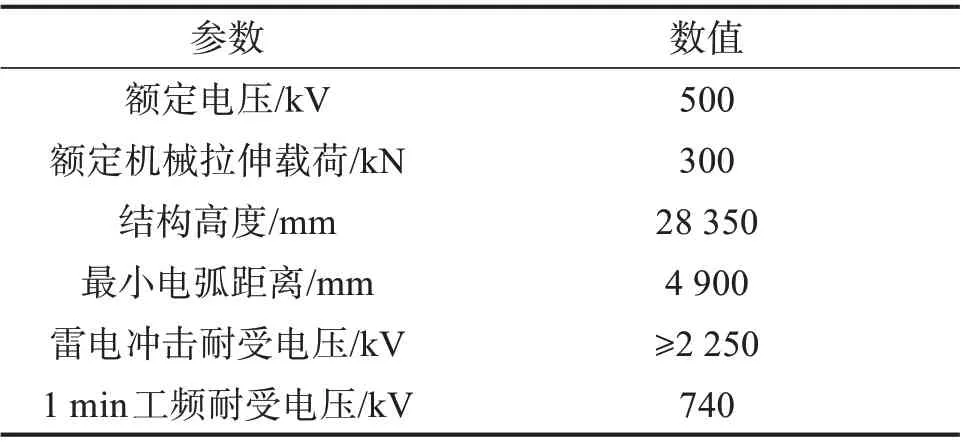
表3 FXBW-500/300SCI绝缘子参数Table 3 Parameters of FXBW-500/300SCⅠinsulator

由于作用于Ⅴ串的重力、风载荷远小于悬挂于其上导线所传递的载荷，在Ⅴ串所受载荷的计算过程中仅考虑导线所传递的风载及其重力，忽略Ⅴ串受到的风载荷及其自重。Ⅴ串不同于普通的瓷质或者玻璃绝缘子串，它能在导线发生最大风偏时产生变形以防止发生破坏。因此，受到横向风作用的时候，Ⅴ串背风侧的单联只发生变形，产生弯矩作用，并对相关金具产生作用。在实际的大风环境中，当Ⅴ串受到的风载荷大于其能承受的安全载荷时，会发生屈曲变形［13］。Ⅴ串屈曲失稳形态如图4所示。

2 复合绝缘子芯棒特征值屈曲特性分析

屈曲分析是用来讨论在特定外力作用下结构自身的稳定性及其失稳时的外力载荷，它通常分为线性屈曲分析和非线性屈曲分析。本文主要对复合绝缘子芯棒进行特征值屈曲分析。

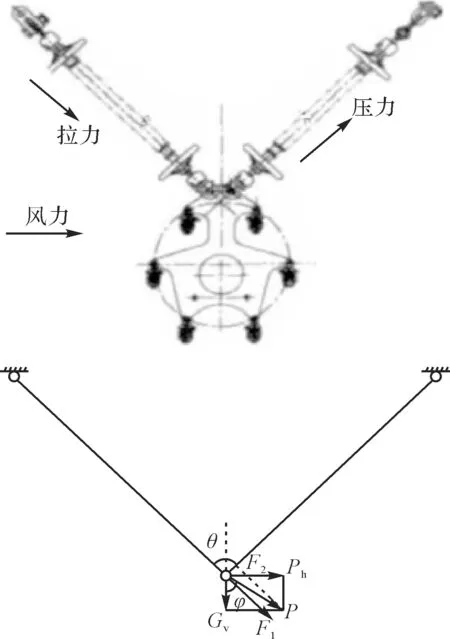
图3 V形绝缘子串受力示意Fig.3 Schematic of stress on Ⅴ-shaped insulator string

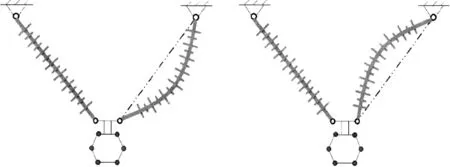
图4 V形绝缘子串屈曲失稳形态Fig.4 Buckling instability pattern of Ⅴ-shaped insulator string

复合绝缘子又称为合成绝缘子，它主要包含芯棒、连接金具和伞裙护套等［14］。芯棒用来承受一些机械载荷，连接金具用来承受并传递载荷，伞裙护套用来加大爬电距离，防止浮尘等污秽在绝缘子表面附着。FXBW-500/300SCⅠ复合绝缘子芯棒尺寸和材料参数如表4所示。

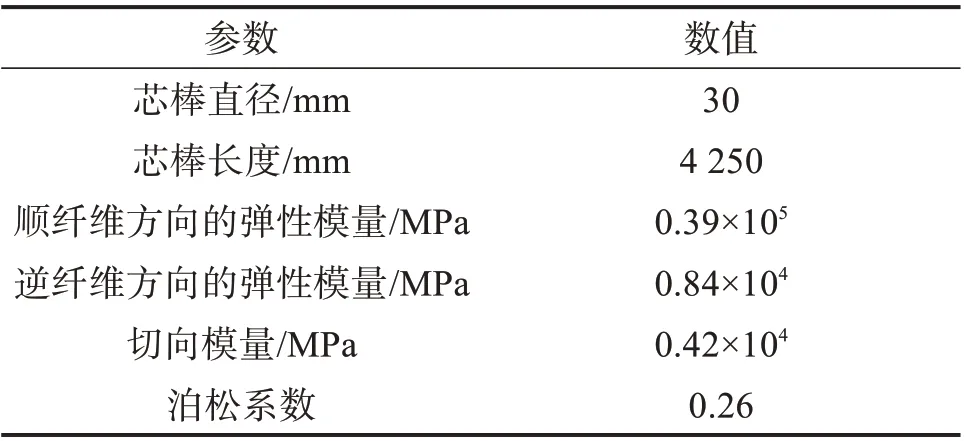
表4 FXBW-500/300SCI复合绝缘子芯棒尺寸和材料参数Table 4 Dimensions and material parameters of FXBW-500/300SCⅠcomposite insulator mandrel

2.1 复合绝缘子芯棒受力的理论分析

本研究中，不考虑芯棒与连接金具衔接处力学性能的影响，将复合绝缘子芯棒看作两端铰支的固定压杆，并将其设定为一种各向同性材料。取其顺纤维方向的弹性模量，即E=0.39×105MPa，泊松系数μ=0.26。

图5所示为两端铰支受压杆件。

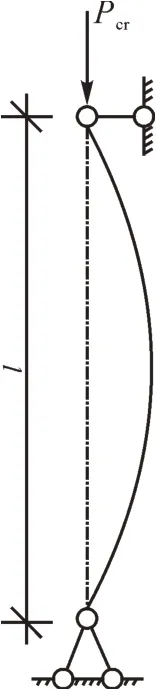
图5 受压杆件Fig.5 Pressure rod

式（1）是在杆件材料符合胡克定律时推导出来的［15］，唯有特定细长杆件才能按照此公式来计算其构件的临界力。经过计算得λ＞100，可判定该杆件为细长杆。通过式（1）算得杆件临界屈曲载荷Pcr=847 N。

有时须考虑临界应力σcr的作用，其表达式为：

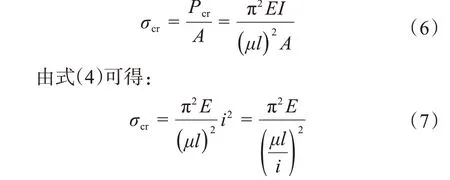
由式（5）可得：

2.2 芯棒特征值屈曲特性的仿真分析

首先，利用ANSYS软件建立复合绝缘串芯棒的有限元分析模型，分别赋予芯棒各向同性和各向异性的材料参数，并对其施加一定的边界条件，进行特征值屈曲仿真分析；取其第1阶解析解并与上文所求的数值进行对比，来验证模型的合理性。

在稳定状态下，考虑轴向力等对杆件受力变形的影响，根据势能驻值定理［16］，杆结构的平衡方程为：

式中：Ke——弹性刚度矩阵；

Kg——几何刚度矩阵，又称为初应力刚度矩阵；

U——结点位移向量；

P——节点载荷向量。

令其二阶变分为零，即：

式中：λi——第i 阶特征值；

φi——与λi对应的特征向量，即为屈曲模态。

2.2.1 基于各向同性的芯棒特征值屈曲分析

利用ANSYS 18.2软件，对受压绝缘子芯棒进行特征值屈曲分析。建模时，仅考虑线性行为，须定义弹性模量；将其材料设置为Beam188梁单元，并进行合理的单元网格密度划分。在进行屈曲分析过程中，进行如下操作：

1）激活预应力效应；

2）若施加单位载荷，则所求结果为屈曲载荷；若施加其他载荷，则须对结果进行合理缩放，才能得到屈曲载荷；

3）施加非零约束。

进行静力分析后，芯棒屈曲载荷仿真结果如图6所示。由图6可知，仿真值与理论计算值相当接近。此时，芯棒发生结构失稳，其一阶屈曲模态如图7所示。

2.2.2 基于各向异性的芯棒特征值屈曲分析

复合绝缘子芯棒通常包含玻璃纤维增强环氧树脂材料［17］，因此可以将它按正交各向异性材料来处理。在对其进行有限元分析时，须赋予其正交各向异性的9个材料参数，包括3个弹性模量、3个剪切模量和3个泊松系数。

图6 基于各向同性的芯棒屈曲载荷仿真结果Fig.6 Simulation result of mandrel buckling load based on isotropy

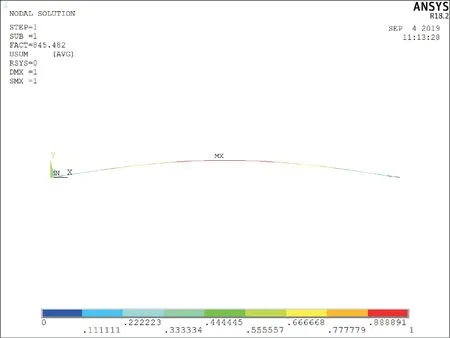
图7 基于各向同性的芯棒一阶屈曲模态Fig.7 First-order buckling mode of mandrel based on isotropy

仿真时，将材料设置为20节点实体单元Solid186。同样，必须激活预应力效应，施加单位载荷以及铰接相关的约束，进行静力分析。提取芯棒屈曲载荷一阶特征值，结果如图8所示。由图8可知，仿真值与理论计算值相差不大，在可接受范围之内。此时，芯棒发生结构失稳，其一阶屈曲模态如图9所示。

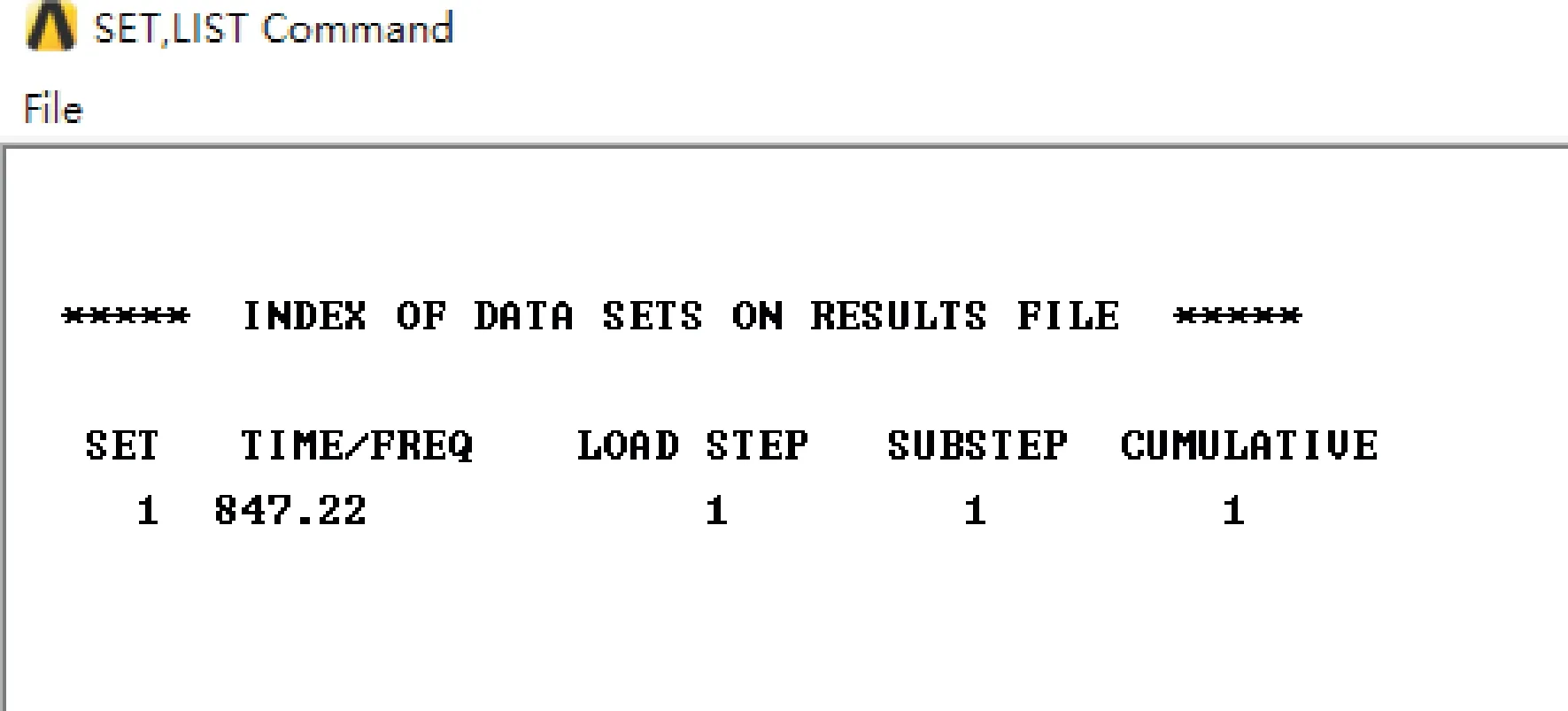
图8 基于各向异性的芯棒屈曲载荷仿真结果Fig.8 Simulation result of mandrel buckling load based on anisotropy

通过以上对比分析可知，与各向同性材料相比，正交各项异性材料对芯棒屈曲载荷及其一阶屈曲模态只有微小的影响，即影响芯棒屈曲载荷大小和屈曲模态的主要因素是顺纤维方向的材料属性。

3 双联与四联V 形绝缘子串在风载荷作用下的力学特性的对比分析

在N45-N46-N47 输电塔线体系中，选取下方绝缘子串作为研究对象。在8～42 m/s风速下，对Ⅴ串的力学特性进行分析。如图10 所示，Ⅴ串的夹角为140°，F、C两点即为Ⅴ串左右两悬挂点。

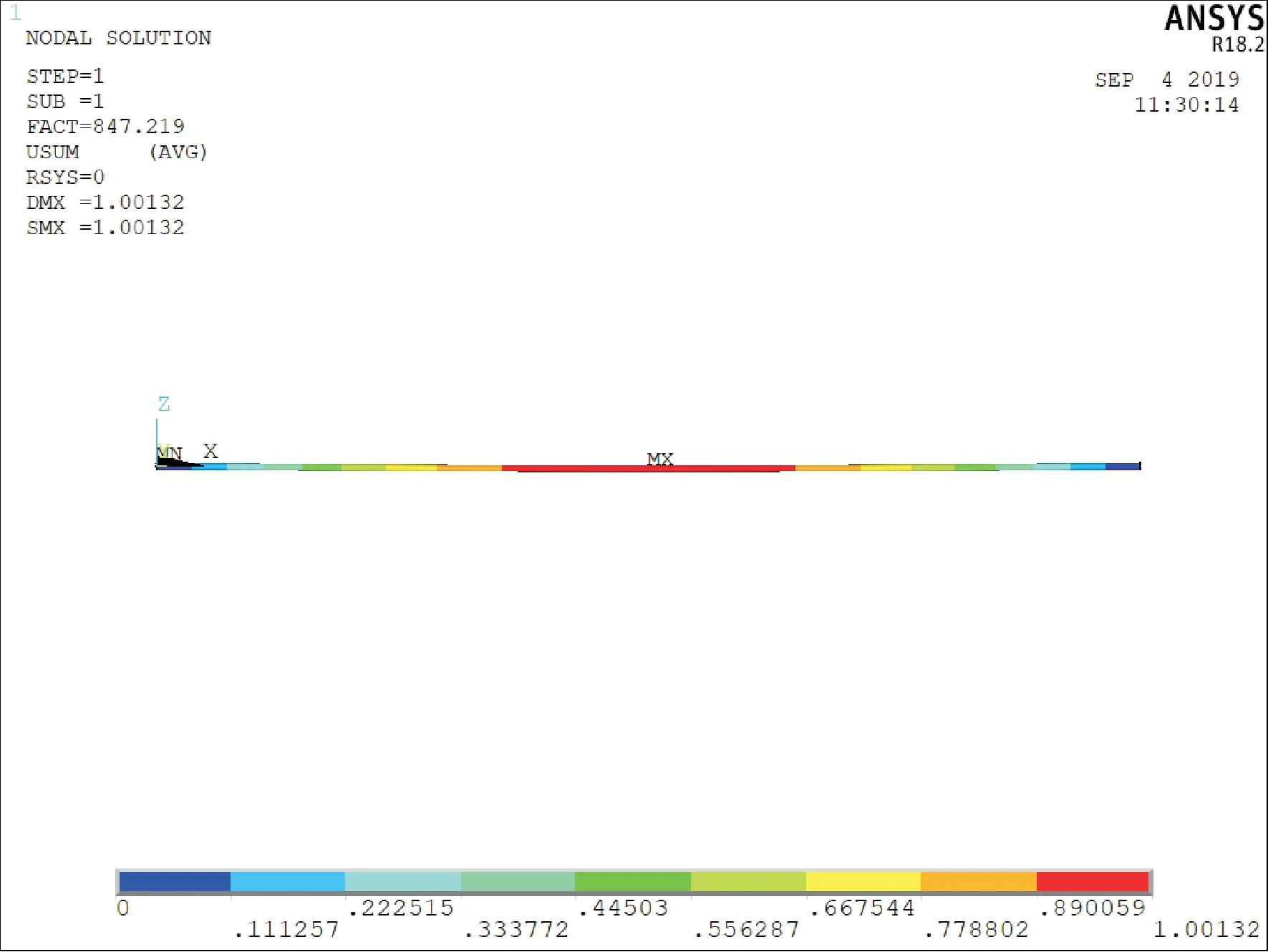
图9 基于各向异性的芯棒一阶屈曲模态Fig.9 First-order buckling mode of mandrel based on anisotropy

图10 夹角为140°的V形绝缘子串Fig.10 Ⅴ-shaped insulator string with an included angle of 140°

在一些自然灾害下，双联Ⅴ串更易发生失稳及受力破损，因此笔者将双联Ⅴ串改为四联Ⅴ串，如图11 所示。在8～42 m/s 风速下，当四联Ⅴ串单联与竖直平面的夹角β=10°，20°，30°时，分别对其力学特性进行分析，并将双联Ⅴ串与四联Ⅴ串的力学特性进行对比。

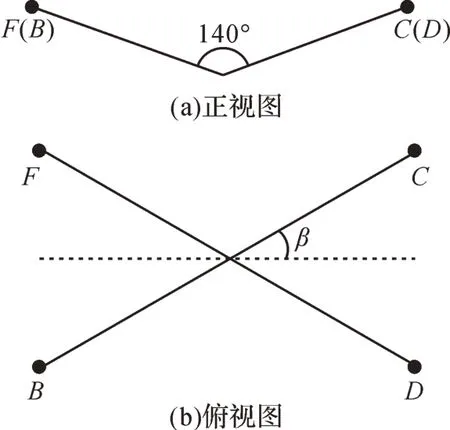
图11 四联V形绝缘子串Fig.11 Quadruple Ⅴ-shaped insulator string

3.1 V形绝缘子串所受载荷计算

在输电塔线体系中，Ⅴ串悬挂点处受到的载荷大小基本等同于输电导线在悬挂点所受到的载荷大小。研究中，忽略绝缘子串、金具、输电地线和输电塔所受到的风载荷以及绝缘子串、金具等的重力载荷的作用，Ⅴ串悬挂点受到的水平载荷即为导线风载荷，垂直载荷即为N46垂直档距内所对应的导线的重力。

N46垂直档距L为：

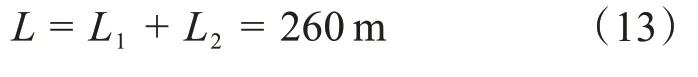
式中：L1——N46左侧档导线最低点与N46之间的距离，m；

L2——N46右侧档导线最低点与N46之间的距离，m。

综合实际情况，Ⅴ串悬挂点受到的垂直载荷为：

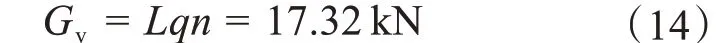
式中：q为导线单位长度质量；n为导线根数。

根据GB 50545—2010《110 kⅤ～750 kⅤ架空输电线路设计规范》［18］，在输电塔线体系中，作用在架空输电导线上的风载荷可计算如下：

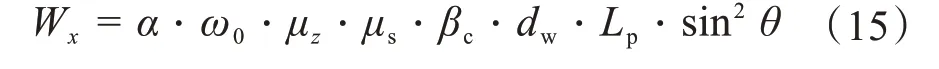
式中：Wx——垂直于线路方向的风载荷，kN；

ω0——基准风压标准值，kN/m2；

α——风压不均匀系数；

μz——风压高度变化系数；

μs——线路的体形系数；

βc——风载荷调整系数；

dw——导线截面直径，若是分裂导线，则取其直径总和，m；

Lp——水平档距，m；

θ——风载荷与线路的夹角，（°）；

v——高度为10 m处的风速，m/s。

结合实际情况选取各参数值，可得在不同风速下Ⅴ串悬挂点受到的水平载荷Ph=Wx，如表5所示。

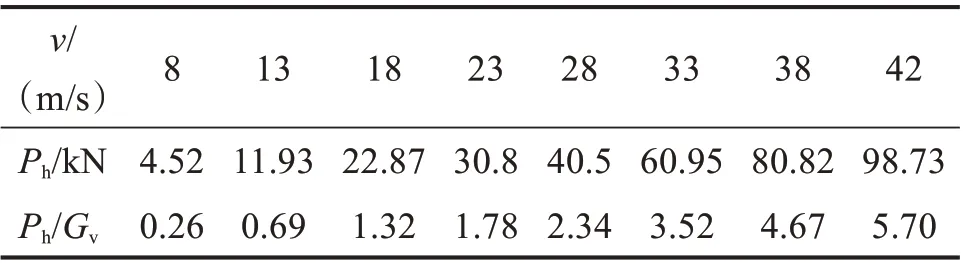
表5 不同风速下V形绝缘子串悬挂点受到的水平载荷Table 5 Horizontal load on suspension point of theⅤ-shaped insulator string at different wind speeds

3.2 双联与四联V形绝缘子串风偏特性分析

3.2.1 Ⅴ形绝缘子串风偏过程

绝缘子串承受垂直载荷Gv和水平载荷Ph。采取依次加载的方式，先对双联Ⅴ串施加垂直载荷，再依次对其施加在8～42 m/s 不同风速下的水平风载荷（风速间隔为5 m/s），来模拟整个风偏过程。

第1步：以施加静力的方式施加垂直载荷，双联Ⅴ串变形结果如图12 所示，可知两边绝缘子串呈悬链线状，自然下垂。其位移云图如图13所示，可知Ⅴ串下面连接点处的位移最大。其应力云图如图14（a）所示，打开形状单元显示开关，可见Ⅴ串基本沿长度方向均匀受力。由图14（b）可知，其最大应力出现在Ⅴ串端头上侧，最小应力出现在端头下侧。

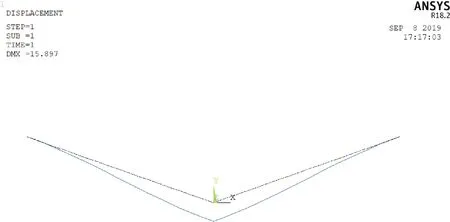
图12 加载垂直载荷后双联V形绝缘子串的变形图Fig.12 Deformation diagram of the bigeminy Ⅴ-shaped insulator string under vertical load

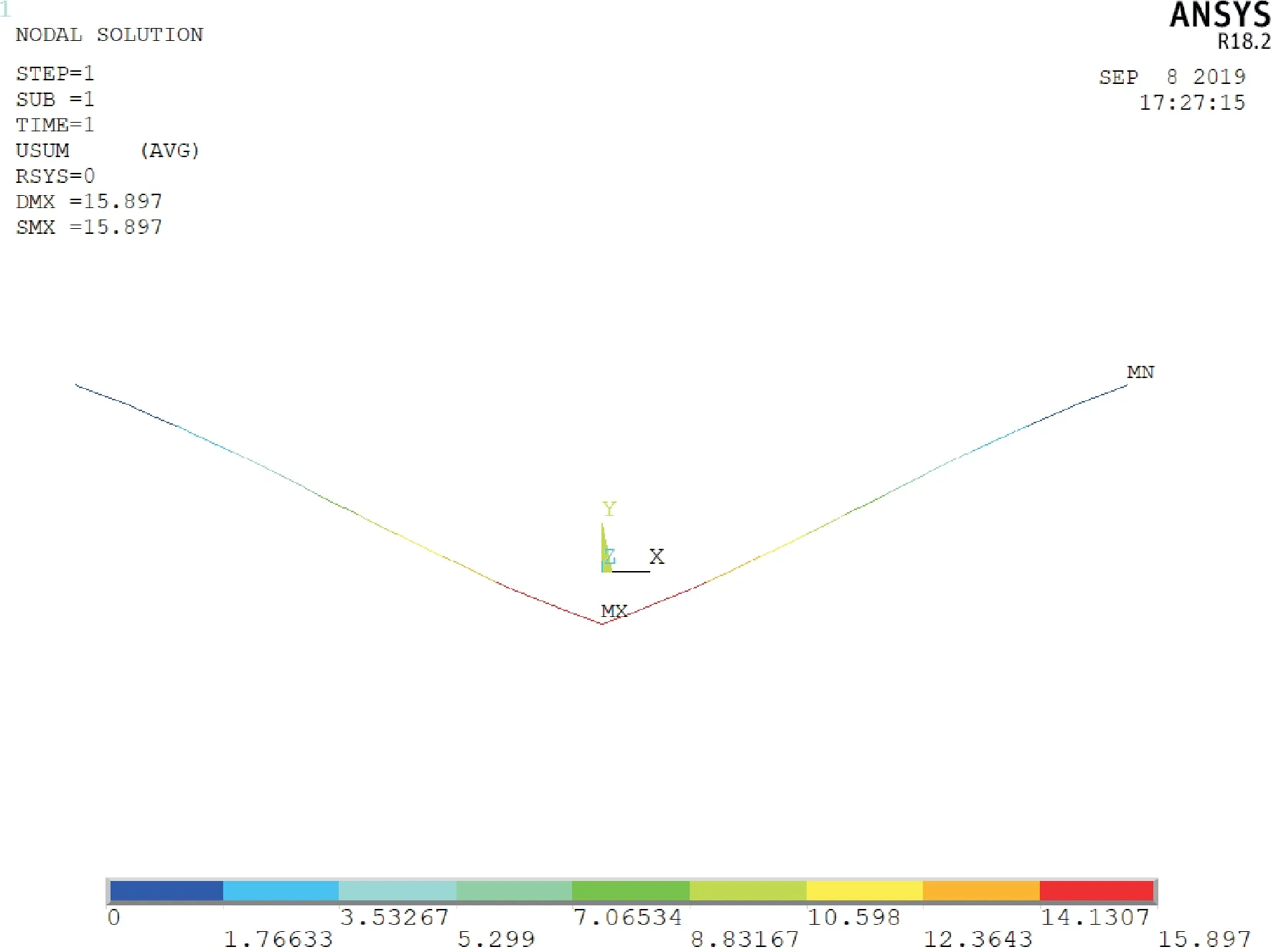
图13 加载垂直载荷后双联V形绝缘子串的位移云图Fig.13 Displacement nephogram of the bigeminy Ⅴ-shaped insulator string under vertical load

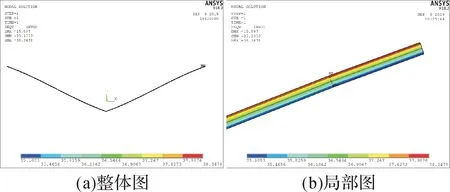
图14 加载垂直载荷后双联V形绝缘子串的应力云图Fig.14 Stress nephogram of the bigeminy Ⅴ-shaped insulator string under vertical load

第2步：施加水平风载荷，选取Ph=98.73 kN进行分析。同样打开形状单元显示开关，即可显示梁单元应力云图，如图15所示，可见双联Ⅴ串的最大应力出现在迎风侧，最小应力出现在背风侧悬挂点处，且Ⅴ串迎风侧受到的应力均比较大，相对于背风侧有比较明显的差异。

对于四联Ⅴ串，分别在β=10°，20°，30°时加载垂直载荷和不同的水平载荷，进行其力学特性仿真。部分仿真结果如图16至图24所示。

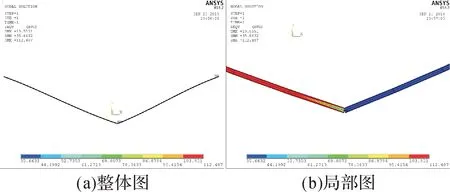
图15 加载98.73 kN 水平面载荷后双联V 形绝缘子串的应力云图Fig.15 Stress nephogram of the bigeminy Ⅴ-shaped insulator string under horizontal load of 98.73 kN

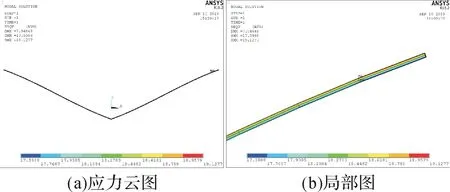
图16 加载垂直载荷后四联V 形绝缘子串的应力云图（β=10°）Fig.16 Stress nephogram of the quadruple Ⅴ-shaped insulator string under vertical load（β=10°）

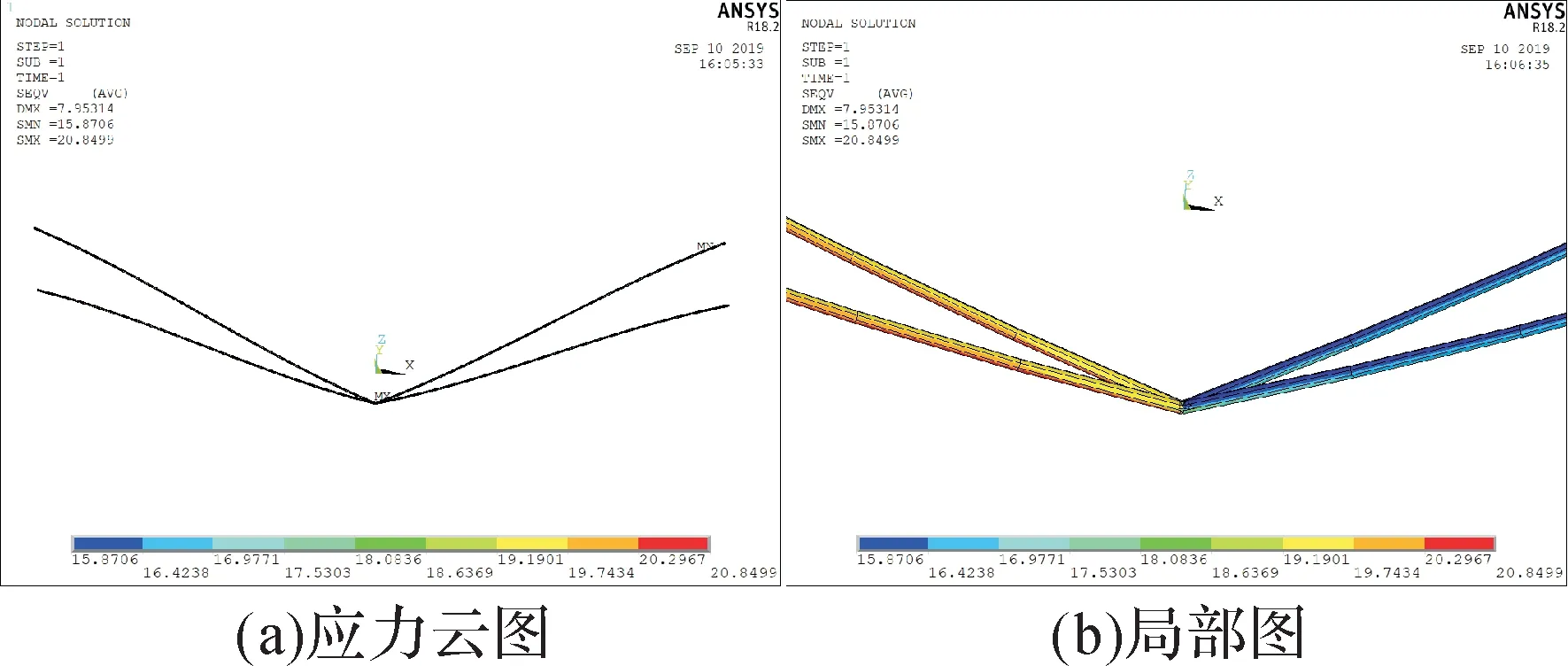
图17 加载水平载荷后四联V 形绝缘子串的应力云图（v=8 m/s,β=10°）Fig.17 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=8 m/s,β=10°）

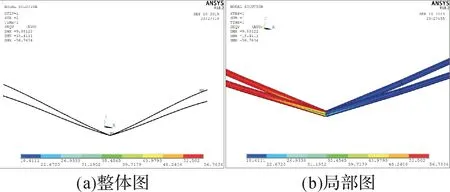
图18 加载水平载荷后四联V 形绝缘子串的应力云图（v=42 m/s,β=10°）Fig.18 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=42 m/s,β=10°）

由仿真结果可知，在垂直载荷作用下，β=10°时，四联Ⅴ串的最大、最小应力均出现在靠近悬挂点连接处；β=20°，30°时，其最大、最小应力均出现在Ⅴ串最低点连接处。继续施加8 m/s的风速，其迎风侧受到的应力较大，且β=10°，20°，30°时的最大应力几乎相等；背风侧受到的应力较小，应力沿绝缘子长度方向基本无变化。当风速达到42 m/s时，其迎风侧受到的应力很大，且应力随β的增大而增大；其背风侧受到的应力都比较小，也随β的增大而增大。

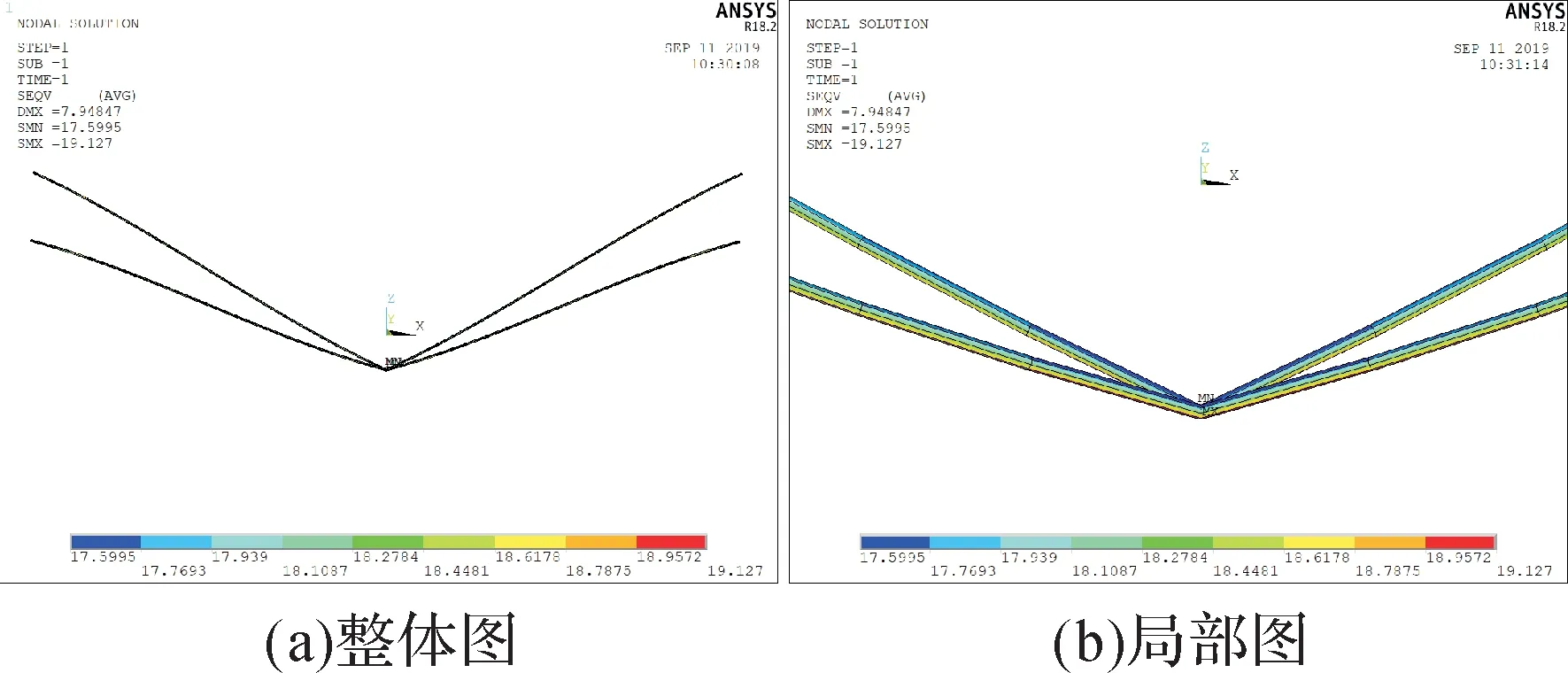
图19 加载垂直载荷后四联V 形绝缘子串的应力云图（β=20°）Fig.19 Stress nephogram of the quadruple Ⅴ-shaped insulator string under vertical load（β=20°）

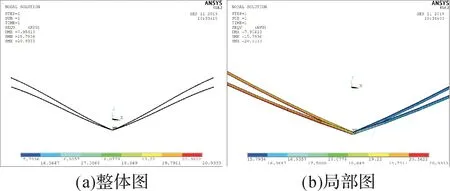
图20 加载水平载荷后四联V 形绝缘子串的应力云图（v=8 m/s,β=20°）Fig.20 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=8 m/s,β=20°）

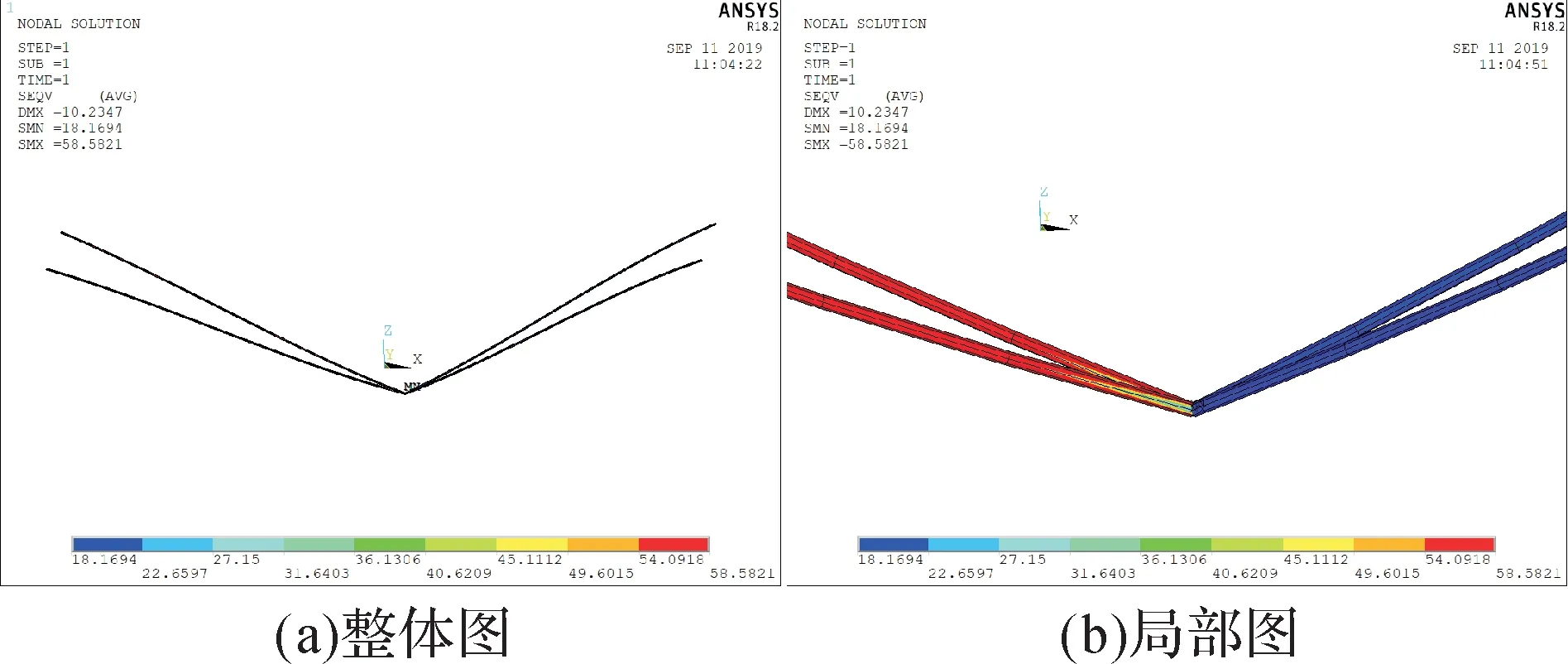
图21 加载水平载荷后四联V 形绝缘子串的应力云图（v=42 m/s,β=20°）Fig.21 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=42 m/s, β=20°）

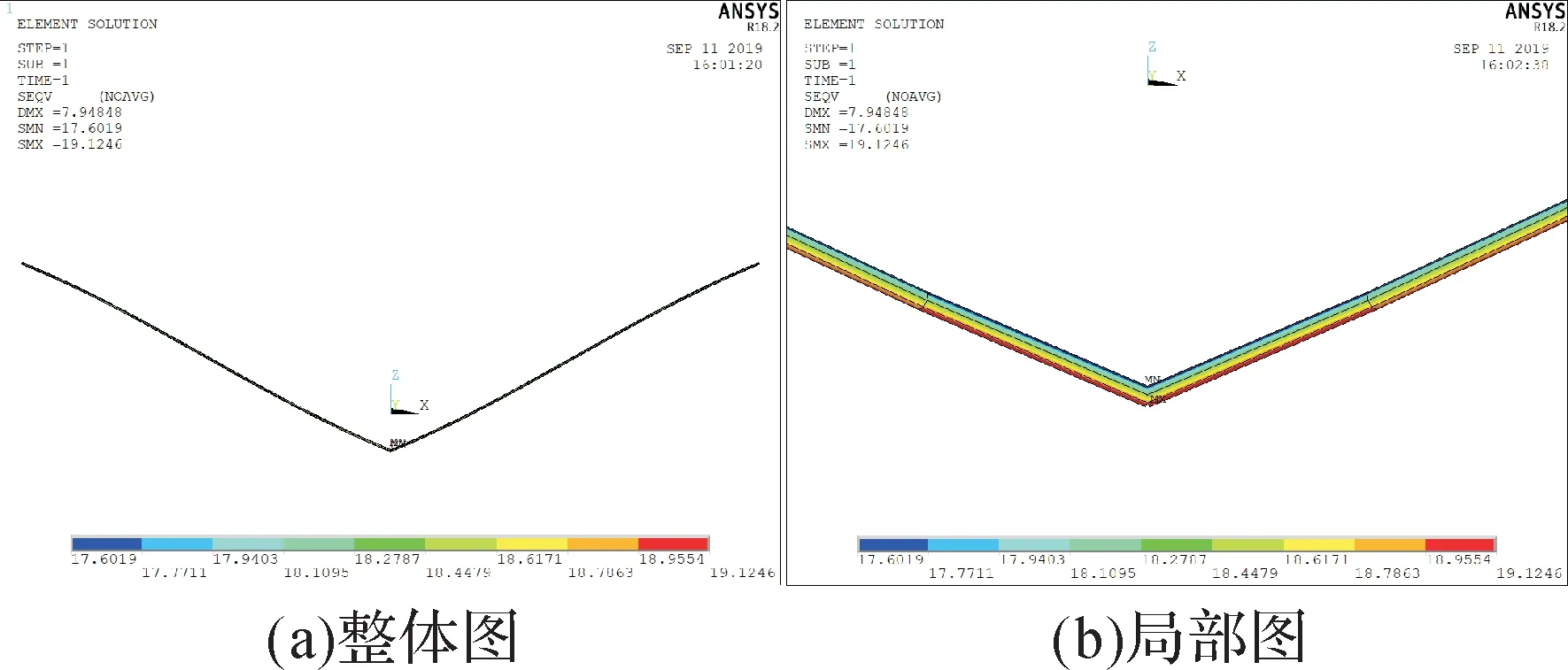
图22 加载垂直载荷后四联V 形绝缘子串的应力云图（β=30°）Fig.22 Stress nephogram of the quadruple Ⅴ-shaped insulator string under vertical load（β=30°）

综上所述，Ⅴ串在外载荷作用下的受力变形过程为：只有垂直载荷作用时，其承受的力主要由两边绝缘子串共同承担，绝缘子串均为受拉状态；当受到垂直载荷和水平载荷作用时，随着水平载荷的不断增大，绝缘子串迎风侧承受更大的外力载荷，背风侧则承受相对较小的外力载荷。

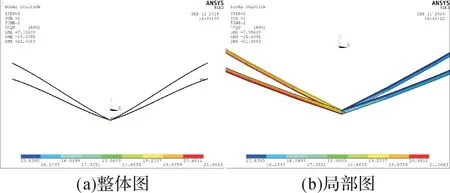
图23 加载水平载荷后四联V 形绝缘子串的应力云图（v=8 m/s,β=30°）Fig.23 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=8 m/s,β=30°）

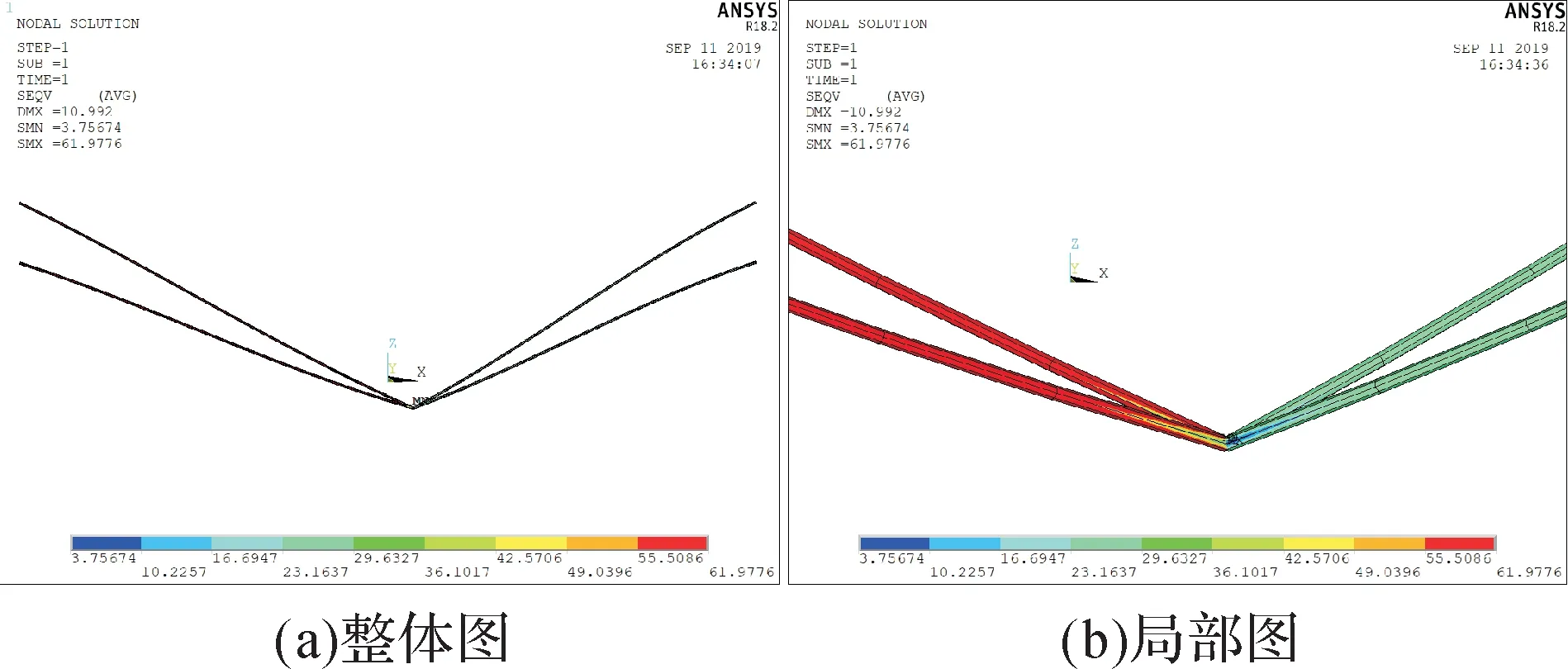
图24 加载水平载荷后四联V 形绝缘子串的应力云图（v=42 m/s,β=30°）Fig.24 Stress nephogram of the quadruple Ⅴ-shaped insulator string under horizontal load（v=42 m/s, β=30°）

3.2.2 Ⅴ形绝缘子串风偏规律研究

在不同风速下Ⅴ串受到的最大应力如表6所示， Ⅴ串最低点的水平位移如表7所示。

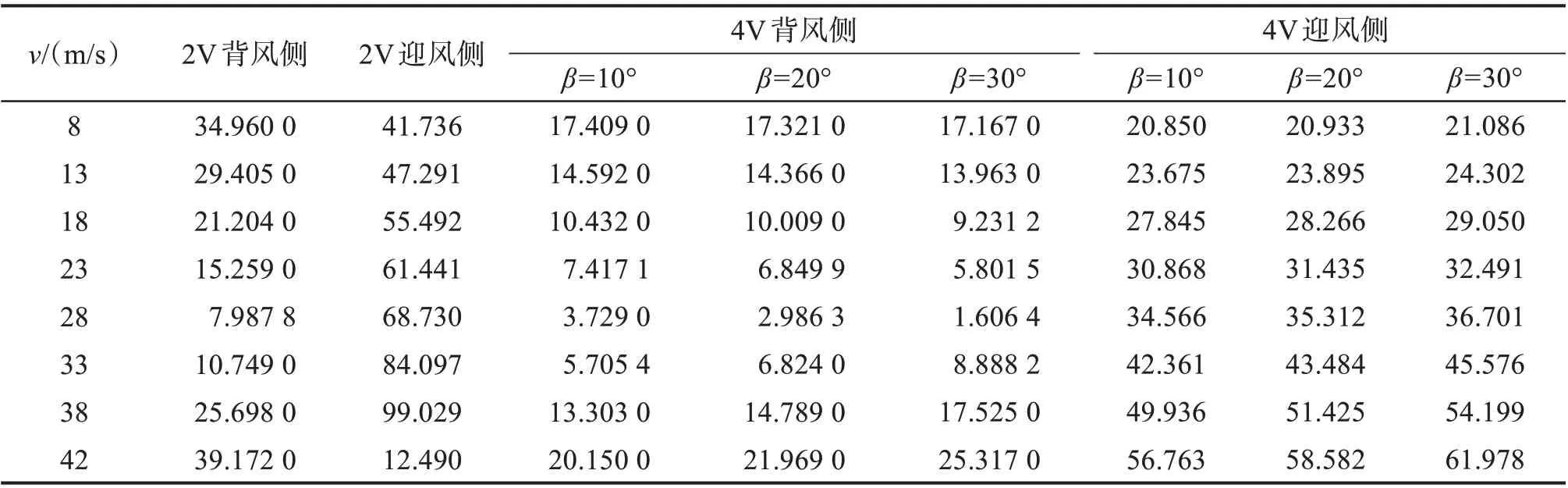
表6 不同风速下V形绝缘子串受到的最大应力Table 6 Maximum stress on Ⅴ-shaped insulator string at different wind speeds 单位：MPa

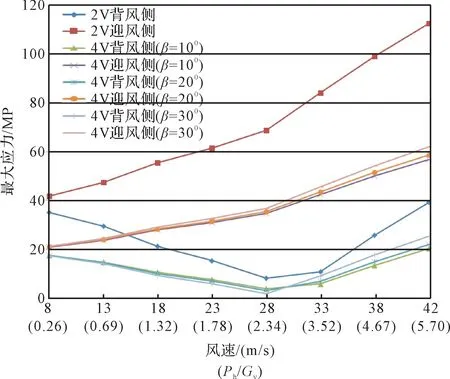
图25 V形绝缘子串所受最大应力与Ph/Gv的关系曲线Fig.25 Relationship curve of maximum stress on Ⅴ-shaped insulator string and Ph/Gv

为分析Ⅴ串风偏规律，研究在不同Ph/Gv下Ⅴ串背风侧、迎风侧所受最大应力的变化情况。Ⅴ串所受最大应力与Ph/Gv的关系曲线如图25所示。Ⅴ串最低点的水平位移与风速的关系曲线如图26所示。

由图25可知：对于迎风侧，不论是双联Ⅴ串还是四联Ⅴ串，其最大应力随着Ph/Gv的增大呈现上升的趋势，且当Ph/Gv＞2.34后，最大应力增速变大，这是由于在水平风载比较小时，Ⅴ串主要表现为垂直载荷对其的影响，而随着Ph/Gv的增大，则逐渐表现为水平风载荷对其的影响，即风速的增加会对Ⅴ串所受最大应力的影响变大。对于背风侧，最大应力随着Ph/Gv的增大呈现先减小后增大的趋势，当Ph/Gv=2.34时，其所受的最大应力最小；在最大应力达到最小之前，β越大，其最大应力减小越快；在最大应力达到最小之后，β 越大，其最大应力增大越快，即β 越大，稳定性越差。

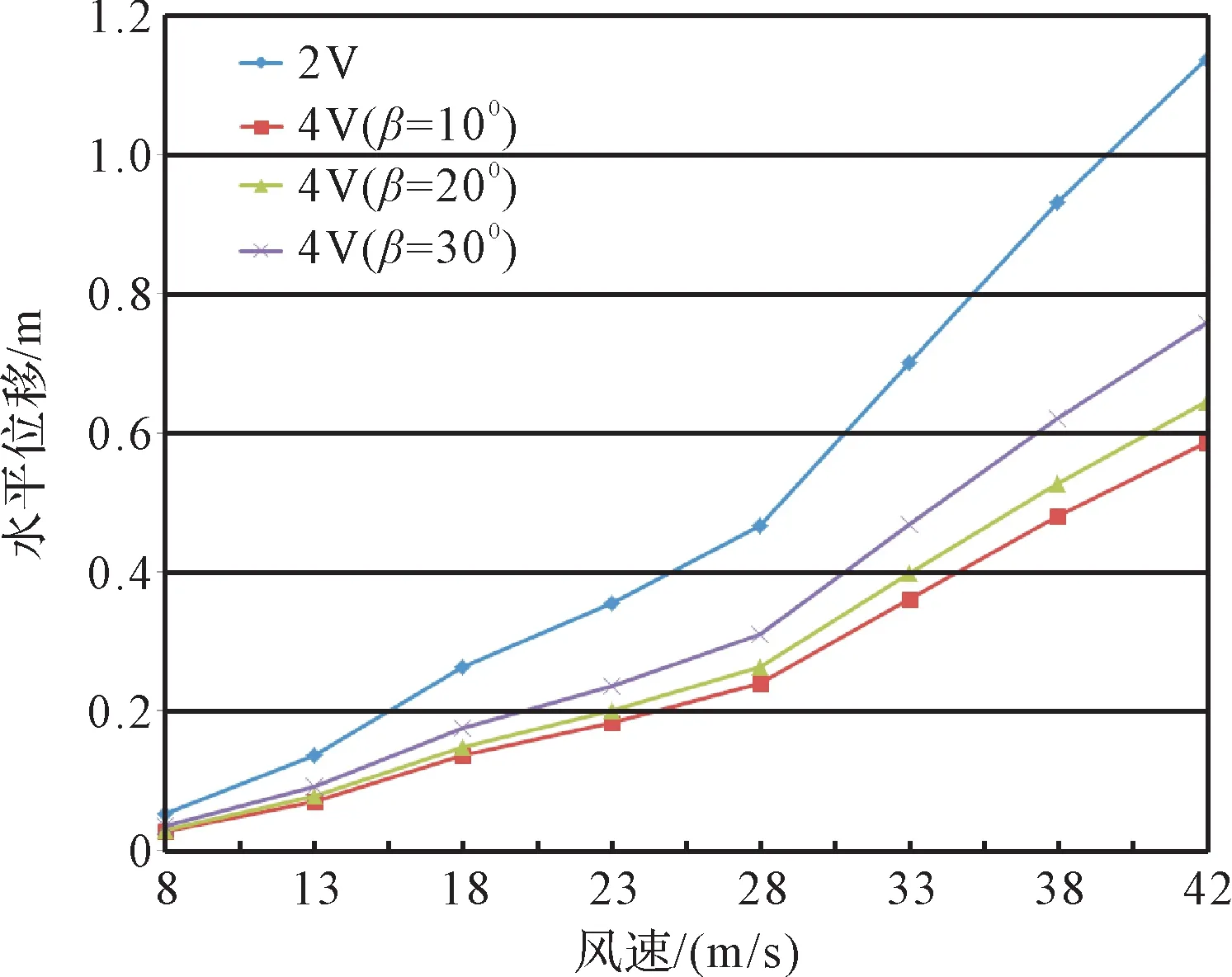
图26 V形绝缘子串最低点的水平位移与风速的关系曲线Fig.26 Relationship curve of horizontal displacement of the lowest point of Ⅴ-shaped insulator string and wind speed

在Ph/Gv增大过程中，四联Ⅴ串的最大应力曲线相比于双联Ⅴ串更加平缓，这表明四联Ⅴ串的性能更加稳定，且β在10°～30°范围内时，β越小，应力曲线越平缓，说明Ⅴ串整体性能越稳定。

综合图25和图26可知，Ⅴ串最低点水平位移的变化大致可以分为3 个阶段：1）在风速较小即Ph/Gv小于一定值时，Ⅴ串最低点在水平方向基本不发生位移，只发生在重力载荷作用下的变形。随着Ph/Gv不断增大，Ⅴ串背风侧承受的载荷逐渐减小，但在这个过程中Ⅴ串最低点的水平位移较小。2）当风速增大到一定值即Ph/Gv达到一临界值时，Ⅴ串背风侧承受的载荷达到最小，外力主要由迎风侧承受。3）当风速持续增大即Ph/Gv超过这一临界值之后，Ⅴ串最低点的水平位移会随着Ph/Gv的增大而快速增大。

由图26还可知，在一定风速下，四联Ⅴ串最低点的水平位移远小于双联Ⅴ串，且β 在10°～30°范围内时，β越小，Ⅴ串最低点的水平位移越小，即结构越稳定，能够更加有效地抵抗外力载荷的作用。