基于扩展雅可比矩阵的冗余液压驱动四足机器人运动控制
2021-03-22陈光荣侯博文王军政
陈光荣,郭 盛,侯博文,王军政
(1.北京交通大学机械与电子控制工程学院,北京 100044;2.北京市轨道交通线路安全与防灾工程技术研究中心,北京 100044;3.北京理工大学自动化学院,北京 100081)
1 引言
目前,机器人和机械臂的研究备受关注[1–2].为了实现更多样化的功能和执行更复杂化的任务,越来越多的机器人和机械臂被设计成具有冗余自由度结构,如线驱动超冗余机械臂[3]、仿人灵巧臂[4]、6R机器人[5]和冗余四足机器人[6]等.
冗余机构的引入提高了机器人和机械臂的功能性和容错能力的同时,也带来了冗余机器人逆运动学求解[7–8]和奇异值规避[9]的问题,提高了控制上的难度.针对此问题,国内外众多学者开展了研究.经典的运逆动学求解算法可分为解析法和优化法,具体有代数法、几何法、奇异值分解算法(singular value decomposition,SVD)、牛顿–拉普森方法、旋量理论法、广义逆法、梯度投影法、扩展雅可比矩阵法和智能优化算法等.Li Shuai 等人提出利用神经网络的方法进行冗余机器人的逆运动学求解,取得了一系列研究成果[10–12],并将运用拓展到含噪声冗余度机器人分布式网络中的协同运动生成[13];基于动态神经网络和非凸约束的冗余度机器人广义重复运动规划方案[14],从优化视角研究冗余度机器人新的干扰抑制约束[15]等.Zhang Zhijun等人对冗余度机器人重复运动规划方案提出3种递归神经网络和3种数值方法[16];对复杂路径规划中双冗余度机器人协调运动提出了三准则优化方法[17];对冗余度机器人关节角漂移问题提出了变参数收敛微分神经网络[18].Guo Dongsheng等人研究了基于伪逆的冗余度机器人噪声环境下PID路径规划新方案[19].Boudreau R等人则利用优化的方法来求解余机器人的逆运动学,目的是最小化驱动力矩[20];此外,各种智能优化算法也成为了冗余机器人的逆运动学求解的重要手段,比如蜂群、蚁群、粒子群、萤火虫算法[21]和遗传算法[22]等.虽然以上几类方法能有效的解决冗余机器人逆运动学求解和奇异值规避问题,但是同时也带来了计算量的提升,对控制器的计算性能要求变高,增加了成本和计算时间.
由于液压驱动具有精度高、响应快、负载能力强等优点[23–25],而四足机器人具有稳定性好,动态特性高等特点[26],液压四足机器人得到了越来越多研究学者的青睐[27–28],而且液压四足机器人中的很大一部分被设计成单腿具有四自由度的冗余结构[29–30],如波士顿动力的四足机器人Bigdog、中国北方车辆研究所的四足机器人“奔跑号”.虽然很多关节角度和关节力矩的优化和约束被添加到冗余四足机器人逆运动学求解中,但目前还没有学者综合考虑冗余四足机器人入地角度、足端工作空间及零力矩点的协调等问题.
因此,针对运动学冗余的液压四足机器人的逆运动学问题,本文提出了一种计算量少,简单易实现的扩展雅可比矩阵法.此方法既能解决机器人运动学冗余问题,还能使机器人入地角度满足摩擦锥的要求以避免足端滑动并满足零力矩点要求[31].通过仿真实验和常用的梯度投影法作了比较,此方法在对角步态(trot)下在实时性上和运动性能上有很好的表现;在斜坡环境下也能平稳的行走.最后又通过实验验证了该方法的可行性和有效性.
2 四足机器人模型
为了提高四足机器人的运动稳定性,本文基于仿生学原理设计了液压驱动仿生四足机器人三维模型,如图1所示,同时建立了机器人载体坐标系{B},髋关节坐标系{H}和足端坐标系{F}.机器人每条腿共有5个自由度:4个主动自由度和1个被动伸缩自由度.4个主动自由度由1个横滚自由度和3个俯仰自由度组成,均由液压缸伺服驱动.其中,髋关节有1个横滚自由度和1个俯仰自由度,膝关节和踝关节各有1个俯仰自由度.髋关节横滚自由度的主要作用是改变机器人行进方向并抵抗侧向干扰与冲击.当受到侧向干扰与冲击时,机器人可通过侧向对角步态快速使机器人恢复姿态平衡和行走稳定.1个被动伸缩自由度由被动伸缩弹簧构成.被动伸缩弹簧可有效减小地面对支撑腿的冲击力,起到良好的缓冲和储能作用,改善机器人的行走稳定性和能源损耗.
四足机器人模型的结构设计参数如表1所示.其中,仿真模型与实物样机的结构参数一致.

表1 四足机器人模型参数Table 1 Model parameters of quadruped robot
以四足机器人右前腿(right fore leg,RF)为例,以髋关节为原点建立前进方向为x轴,竖直方向为z轴的符合右手原则的髋关节坐标系{H},如图2所示.
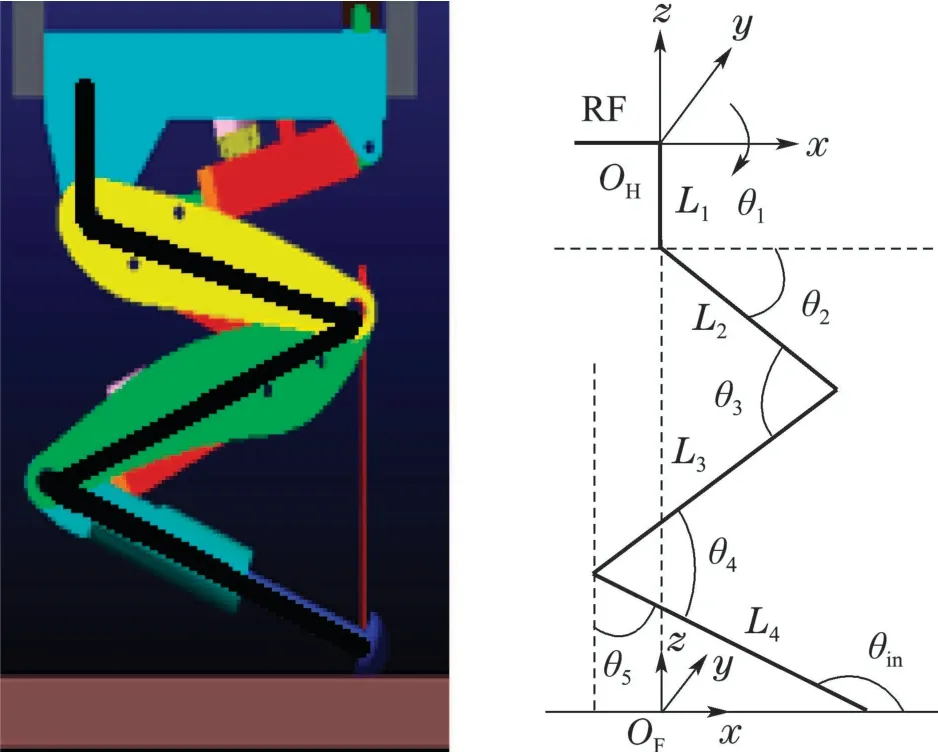
图2 机器人单腿配置与坐标系Fig.2 Configuration of single leg of quadruped robot
在图2中,θ1为髋关节侧摆角,θ2为髋关节俯仰角,θ3为膝关节俯仰角,θ4为踝关节俯仰角,θ5为机器人足端末端杆件与竖直方向夹角,θin为足端入地角.以上各关节角度运动范围限制如表2所示.注意,由于θ2,θ3,θ4的角度运动范围限制,致使四足机器人不可能出现奇异位置或处于奇异位置附近,即在逆运动学解算时,避免了考虑奇异值规避问题,不会出现无解和解的病态程度很高的情况.

表2 机器人腿部各关节角度运动范围限制Table 2 The range of joint angle of leg of quadruped robot
3 足端轨迹规划
四足机器人在行走过程中,每条腿均由支撑相和摆动相组成,并在支撑相和摆动相间来回切换,从而完成机器人的行走运动.其中,摆动相是指腿部从抬腿时足端离地到落腿时足端触地期间的相位变化过程;支撑相是指腿部从落腿时足端触地到再次抬腿时足端离地期间腿的相位变化过程.
由于改进的摆线方程可实现机器人足端轨迹速度和加速度的连续变化,故本文在足端坐标系{F}下,采用改进的摆线方程对机器人足端轨迹进行规划.当足端处于支撑相时,其在竖直方向上没有位移运动,使用摆线方程规划足端水平方向的运动,引导足端的加减速.当足端处于摆动相时,其在水平和竖直方向上均有位移运动和加减速过程.整体足端轨迹规划为
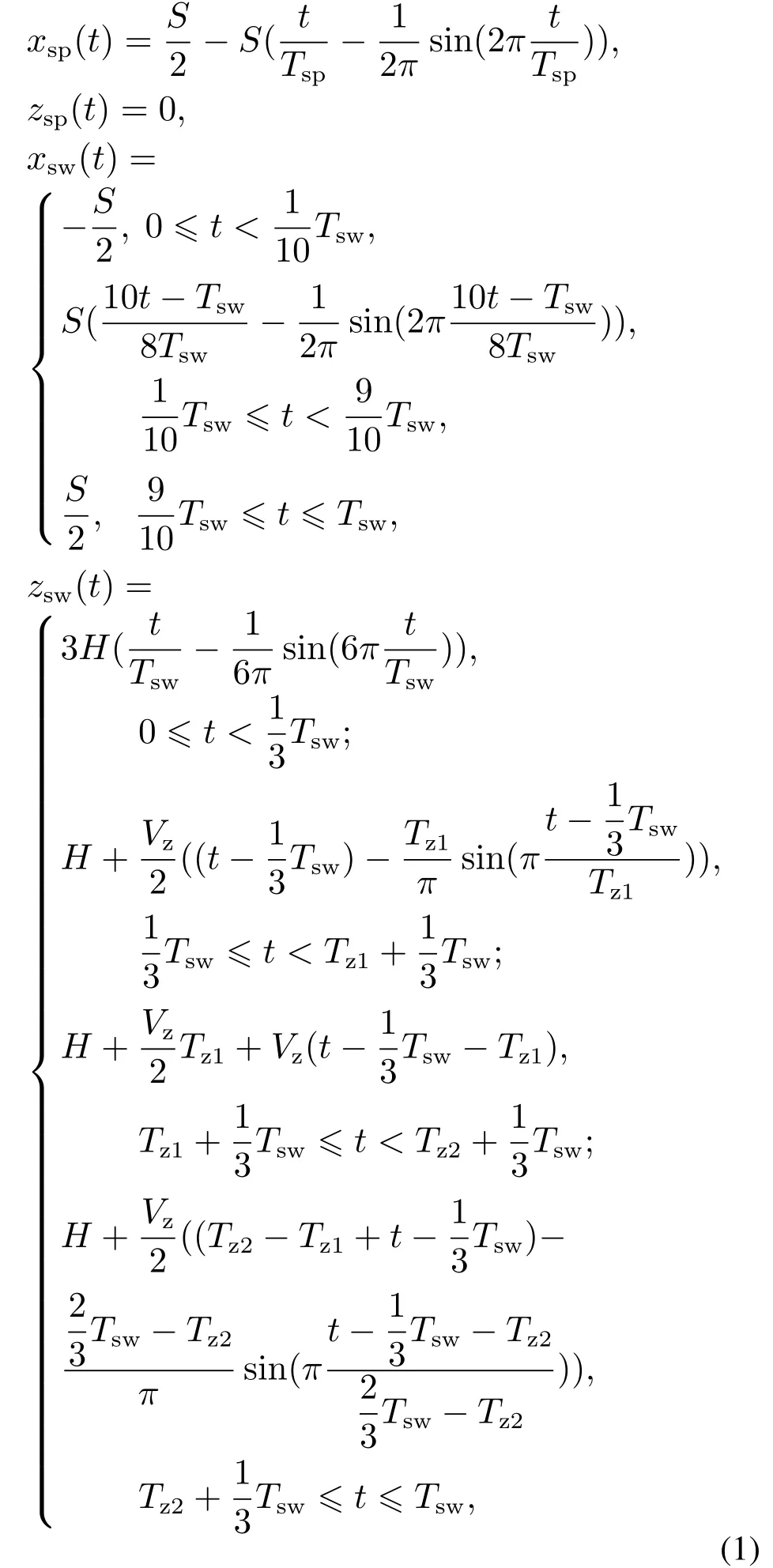
式中:(xsp(t),ysp(t)),(xsw(t),zsw(t))分别是支撑相和摆动相的步态规划足端坐标;S是步幅长度;Tsp,Tsw分别是支撑相和摆动相周期;H是抬腿高度;Vz是足端落地过程中的最大速度;Tz1,Tz2−Tz1,−Tz2分别是机器人足端从抬腿高度H减小到零过程中所经过的加速时间、匀速时间和减速时间,这3个值可自行设定或通过实验调节,但须满足大小关系:Tz1<如此一来,机器人足端在水平和竖直方的速度和加速度的变化都是连续可导的,不会产生足端速度和加速度的突变,使足端轨迹更加平滑,有效避免了机器人与地面的硬接触,同时接触力方向也容易满足摩擦锥的要求.
4 逆运动学分析
因为有冗余自由度的存在,冗余四足机器人在运动学上可以根据实际需求进行多种性能优化,使机器人足端的工作空间更大,运动性能和越障能力更强,复杂环境适应性更高.冗余度机器人的逆运动学分析和性能优化方法有多种.本文通过设计自选的优化函数构建扩展雅可比矩阵来对冗余四足机器人进行性能优化,并与基于梯度投影法的逆运动学分析方法进行对比.
假设四足机器人躯干与地面平行,且只有直线运动没有外摆运动,则侧摆角度θ1为0.根据机器人腿部几何关系可解算出机器人足端与杆长和关节角之间的运动学关系.由图2可知,足端在髋关节坐标系{H}下的坐标:
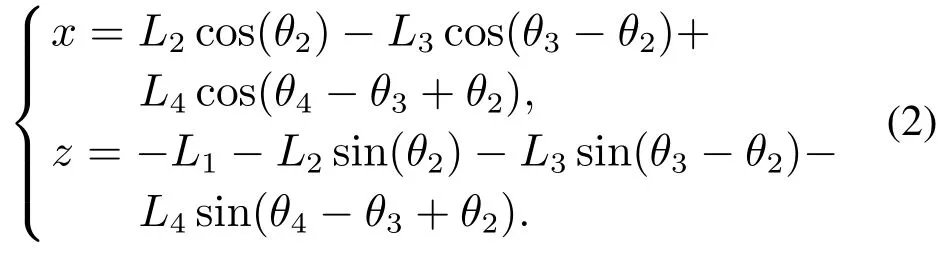
对式(2)两边同时求导,可得雅可比矩阵为

其中:X[x z]T是机器人足端在髋关节坐标系{H}下的坐标;θ[θ2θ3θ4]T是机器人腿部各关节角度;雅可比矩阵J其中:
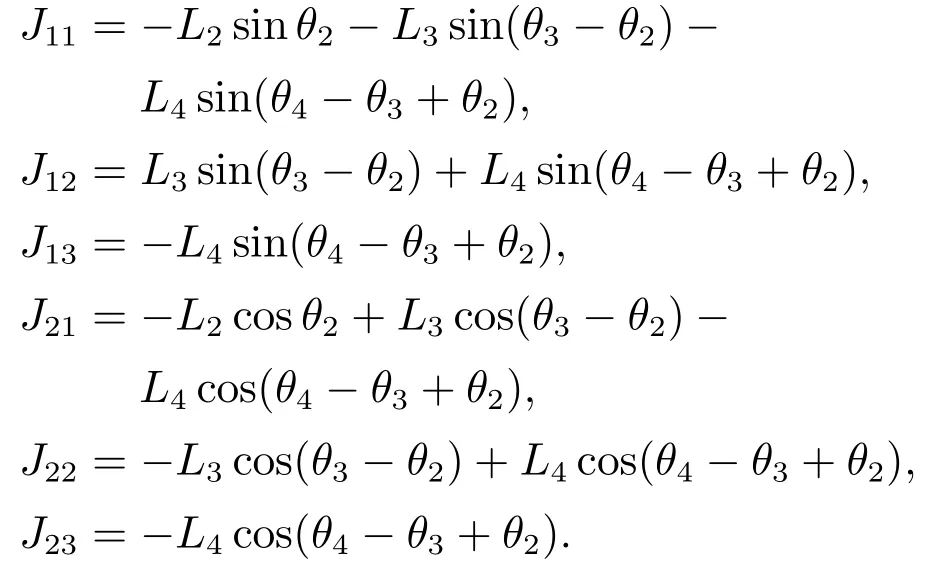
由式(2)–(3)可知,式(3)中的雅可比矩阵为胖矩阵,方程(2)求解存在未知数个数大于方程个数情况(3>2),即存在冗余度.冗余四足机器人在运动过程中,其逆运动学求解中存在各关节角度多解现象.以下主要通过梯度投影法和扩展雅可比矩阵法这两种方法进行逆运动学求解,并比较二者在解决冗余四足机器人逆运动学问题上的优劣.扩展雅可比矩阵法主要是通过增加性能优化函数作为额外的约束方程,引入到式(3)中的雅可比矩阵,从而使方程存在唯一解,且满足给定的性能优化指标.
4.1 梯度投影法
式(3)给出了机器人足端速度和腿部各关节角速度之间的关系,设J+∈Rn×m是雅可比矩阵的广义逆;k为自运动的放大系数;(I −J+J)是零空间梯度投影矩阵;∇ϕ ∈Rn为任意待优化目标函数ϕ(θ)的梯度.则冗余四足机器人关节角速度反解为:
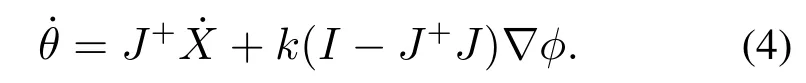
式中:J+JT(JJT)−1;右式第1项J+是冗余四足机器人的最小范数解,右式第2项k(I −J+J)∇ϕ是自运动项,用来优化机器人运动学各项性能指标.对冗余四足机器人自运动的优化是通过调整放大系数k和待优化目标函数ϕ(θ)的梯度∇ϕ来实现的.针对运算过程中可能出现的奇异点问题,可采用文献[9]中所提的方法,引入阻尼系数λ,可规避奇异点.易知,梯度投影法得到的关节角速度式(4)容易存在累计误差,尤其是多次迭代计算会造成更大的累计误差.
4.2 扩展雅可比矩阵法
4.2.1 扩展雅可比矩阵法
对式(1)基于改进摆线方程规划的四足机器人足端轨迹两边求导,可得到机器人足端速度与腿部各关节角速度之间的关系.由式(3)可知,此方程组由两个方程3个未知数组成,是不定方程组,有无数组解.若能找到机器人某个性能指标函数ϕϕ(θ),其对关节角度的梯度为

然后将式(3)和式(5)联立得
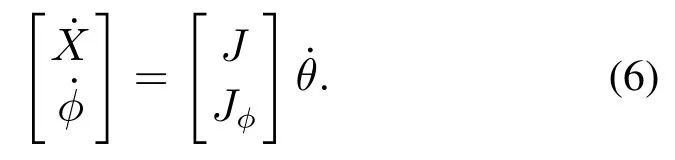
再定义扩展雅可比矩阵Je为:

可以看出扩展雅可比矩阵Je是方阵,方程个数与未知数个数相等.同时文献[1]也给出了性能指标函数如何规避奇异值的方法.
在给定腿部各关节角度运动范围条件下(表2),四足机器人腿部均处于非奇异位置,即,便能得到关节角度的唯一解,即可解得关节角度的解析解

4.2.2 入地角度性能指标函数规划
由图2可知,角度θ2,θ3,θ4,θ5存在如下关系:
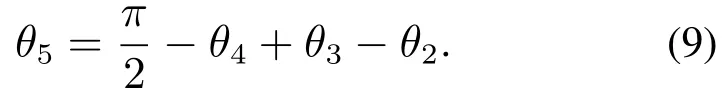
其中θ5与入地角度θin又存在如下关系;

而四足机器人足端与地面接触时,为了防止机器人足端与地面产生滑动,其足端必须满足摩擦锥的要求.如图3所示,设四足机器人足端与地面接触力为F,当接触力的水平分量Fx超过地面的最大静摩擦力时,即Fx>µFz,Fx位于摩擦锥之外,其中µ为静摩擦系数,则足端与地面之间将会产生相对滑动.若仅考虑四足机器人足端受力情况和地形摩擦系数,则可定义摩擦锥的角度为:αtan−1µ.为保证四足机器人足端不打滑,应该保证接触力F与竖直方向的夹角θ小于摩擦锥的角度α.
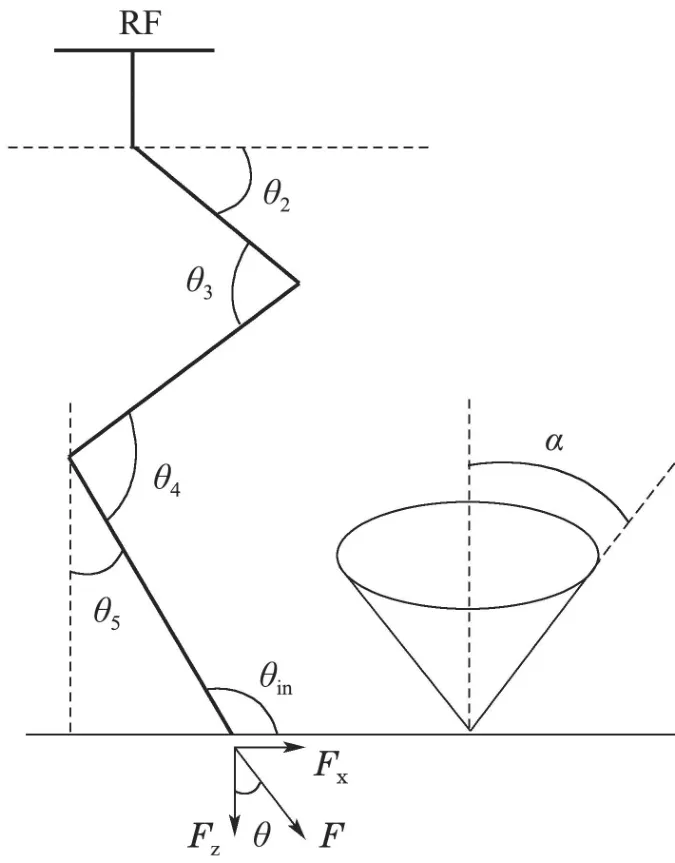
图3 足端摩擦力与摩擦锥示意图Fig.3 Configuration of single leg of quadruped robot
在实际运动过程中,受机器人足端轨迹影响,机器人足端末端杆件与地面接触力并不共线,即机器人足端入地角度θin和接触力F与竖直方向的夹角θ并不相等.故可在足端轨迹规划中加入入地角度θin性能指标约束,使机器人足端落地时在竖直方向上的受力较大,即可保证足端满足摩擦锥要求.由于θ5的角度值约束不同,四足机器人足端的工作空间不同,θ510◦和θ540◦时足端在髋关节坐标系{H}下的工作空间分别如图4和图5所示.由图可知,单腿工作空间在θ5的某些给定值约束条件下变得比较小,在此类约束下进行足端轨迹规划将使步态的步长S和步高H受限严重.如果使用单一固定的θ5进行足端轨迹规划一定程度上会大大削弱机器人的运动性能.因此,进行入地角度约束时应尽量避免以上弊端,采用时变的θ5.
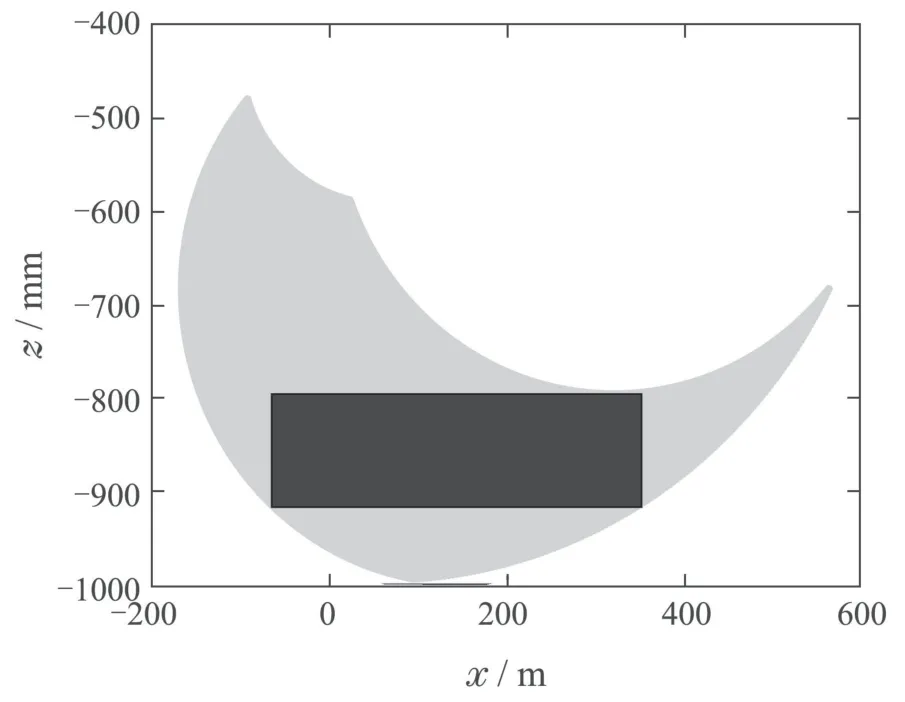
图4 θ5=10◦时的足端工作空间Fig.4 Workspace of foot end effector when θ5=10◦
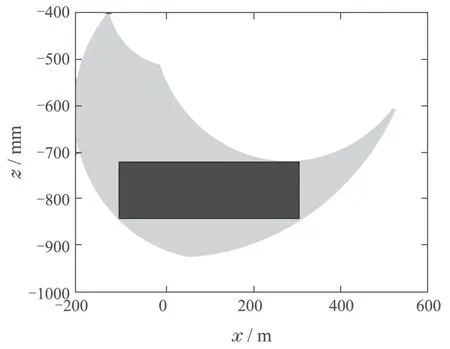
图5 θ5=40◦时的足端工作空间Fig.5 Workspace of foot end effector when θ5=40◦
四足机器人足端运动呈周期性步态运动,故θ5的性能指标函数给定也应是周期函数.综上考虑,设
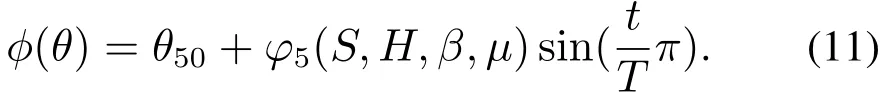
由式(9)得
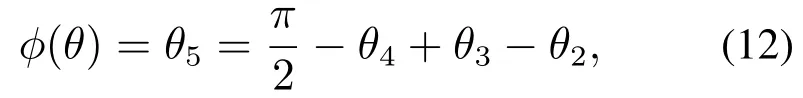
其中:θ50是机器人一个步态开始时θ5的初始值;T是整个步态周期;φ5(S,H,β,µ)是θ5的周期性变化幅值,其大小受足端工作空间、步态参数S,H、地面坡度β及静摩擦系数µ等影响.至此便可计算出扩展雅可比矩阵Je,且是方阵.计算扩展雅可比矩阵的行列式为
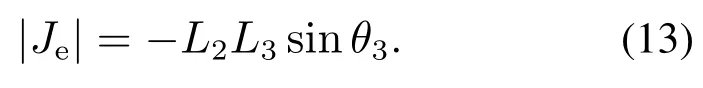
由于四足机器人腿部机械结构和关节角度运动范围限制(表2):θ3∈(0,π),故由于四足机器人腿部机械结构和关节角度运动范围限制.因此在机器人足端工作空间内,由足端轨迹规划式(1)和θ5的性能指标函数约束可以得到唯一的腿部各关节角度解析解,即θ2,θ3,θ4的值,从而完成冗余四足机器人腿部基于入地角度性能指标函数规划的逆运动学解算.
4.2.3 髋关节角度性能指标函数规划
同样地,除了可以对θ5的性能指标函数进行约束,也可以对θ2,θ3,θ4进行性能指标函数约束.四足机器人在对角步态(trot)正常行走时,主要是通过膝关节θ3和踝关节θ4的运动实现腿部摆动,髋关节θ2的运动幅度相对较小.因此,在此使用相同方法给出髋关节角度性能指标函数规划如下:
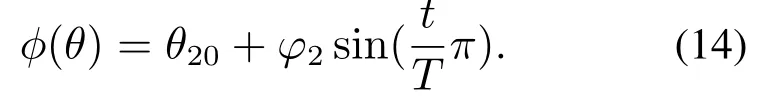
由式(9)得
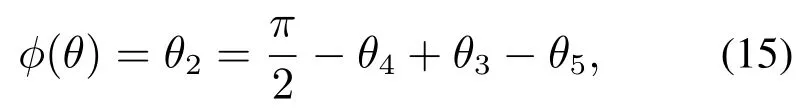
其中:θ20是机器人一个步态开始时θ2的初始角度,φ2是θ2周期性变化幅值.从而可得其扩展雅可比矩阵Je,且其行列式为
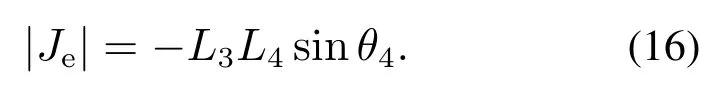
由于四足机器人腿部机械结构和关节角度运动范围限制(表2):θ4∈(0,π),故.因此在机器人足端工作空间内,由足端轨迹规划式(1)和θ2的性能指标函数约束可以得到唯一的腿部各关节角度解析解,即θ3,θ4,θ5的值,从而完成冗余四足机器人腿部基于髋关节角度性能指标函数规划的逆运动学解算.
5 仿真实验
本文利用SolidWorks(2016)软件设计机器人结构模型,并将其导入到Adams(2017)软件中作为虚拟样机,如图1所示.然后通过MATLAB(R2018b)和Adams联合仿真验证算法的有效性.仿真参数如表3所示.
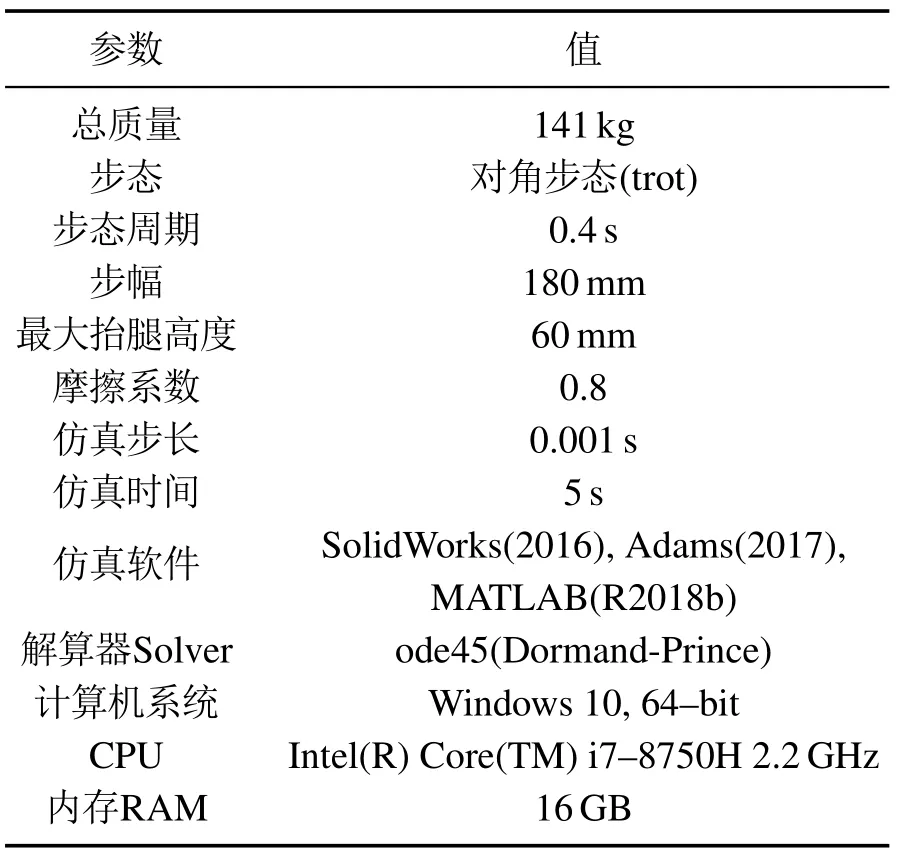
表3 仿真参数Table 3 Simulation parameters of quadruped robot
5.1 梯度投影法
在梯度投影法中,取参数k−1,优化目标函数ϕ(θ)为简单的髋关节运动函数,仿真结果如图6所示,其中足端竖直向上线为接触力,线的长短反映了力的大小,箭头反映了力得方向.
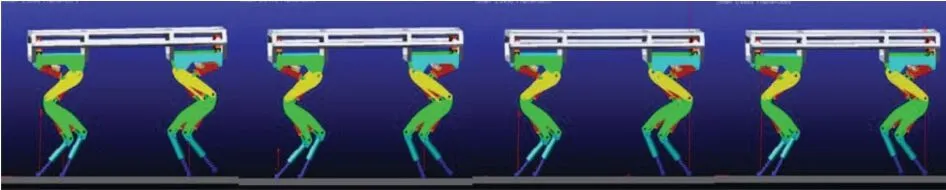
图6 梯度投影法trot行走仿真Fig.6 Simulations of trot walking with gradient projection method
图7为仿真中四足机器人右前腿各关节角度随时间的变化曲线.由图可知,θ2,θ3,θ4三个关节角均随时间呈现周期性变化规律.θ2,θ4在规律变化的同时,整体大小有微小幅度的增加;而θ3在规律变化的同时,整体大小有明显幅度的减小.此现象说明梯度投影法的逆运动学求解存在累计误差影响.而且,整个仿真过程运行速度较慢,花费时间较长.

图7 梯度投影法trot行走仿真机器人右前腿关节角度Fig.7 Joint angles of right fore leg of robot in simulations of trot walking with gradient projection method
5.2 扩展雅可比矩阵法
以入地角规划式(11)为性能优化函数进行扩展雅可比矩阵法的逆运动学求解,并仿真验证,结果如图8所示.图9为仿真中四足机器人右前腿各关节角度随时间的变化曲线.由图可知,θ2,θ3,θ4三个关节角均随时间呈现周期性变化规律,且整体大小保持恒定,不存在增大或减小趋势.而且,整个仿真过程运行速度相对较快,花费时间相对较短.
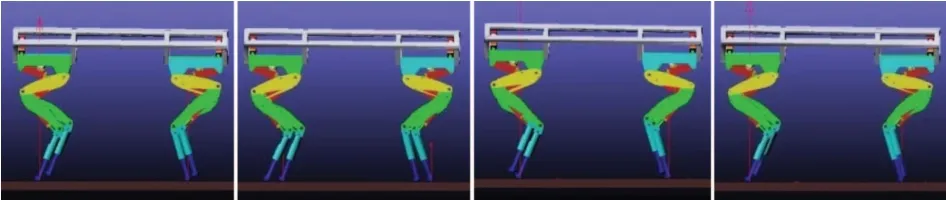
图8 扩展雅可比矩阵法trot行走仿真(θ5/θin)Fig.8 Simulations of trot walking with extended Jacobian matrix method(θ5/θin)
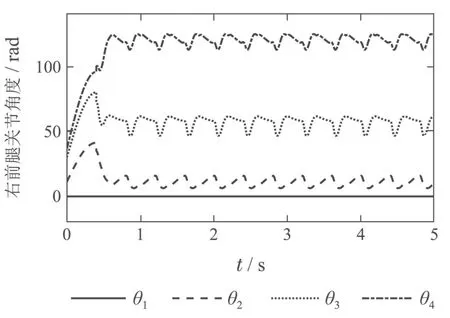
图9 扩展雅可比矩阵法trot行走仿真机器人右前腿关节角度(θ5/θin)Fig.9 Joint angles of right fore leg of robot in simulations of trot walking with extended Jacobian matrix method(θ5/θin)
同样地,以髋关节角规划式(14)为性能优化函数进行扩展雅可比矩阵法的逆运动学求解,并仿真验证,结果如图10所示.图11为仿真中四足机器人右前腿各关节角度随时间的变化曲线.由图可知,θ2,θ3,θ4三个关节角也均随时间呈现周期性变化规律,且整体大小也保持恒定,也不存在增大或减小趋势.而且,整个仿真过程运行速度和花费时间与以入地角规划式(11)为性能优化函数的方法相差无几.
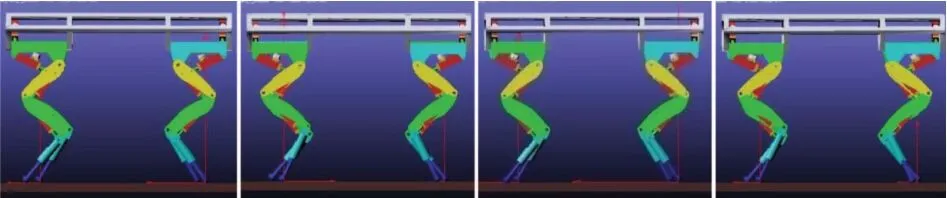
图10 扩展雅可比矩阵法trot行走仿真(θ2)Fig.10 Simulations of trot walking with extended Jacobian matrix method(θ2)

图11 扩展雅可比矩阵法trot行走仿真机器人右前腿关节角度(θ2)Fig.11 Joint angles of right fore leg of robot in simulations of trot walking with extended Jacobian matrix method(θ2)
5.3 机器人斜坡trot步态行走
Trot步态是四足动物最常用的步态,也是四足机器人研究最多的步态.该步态具有较高的动态性能,也具有一定的动态稳定性.四足机器人在平坦地面上trot步态行走时,其质心投影点通常落在腿部支撑区域中心附近,具有较高的相对运动稳定性.但四足机器人在斜坡地形上采用完全相同的trot步态行走而不做任何步态修正时,随着坡度的增大,其质心投影点离腿部支撑区域边界线的距离越近,甚至跑出支撑区域,此时机器人的运动稳定性越来越差,甚至失稳.虽然四足机器人能够在质心投影点偏离支撑区域时,及时地交替对角支撑腿以达到动态稳定,但该调整会造成机器人躯干摇摆不定,大部分时间处于姿态控制阶段,而不是行进控制阶段,不利于机器人稳定行走.针对此问题,可以通过调整机器人腿部入地角度来改变支撑区域位置,使机器人质心投影点更加靠近支撑区域中心以提高机器人运动稳定性,如图12所示.其本质也是机器人trot步态在上下斜坡行走时,可以通过调整机器人质心前后移动,以保持其零力矩点投影更加靠近对角支撑腿足端连线,至少应当保证其零力矩点落在虚拟支撑区域内,即对角摆动腿的落脚点和对角支撑腿的足端点组成的支撑区域内.

图12 机器人斜坡trot步态行走足端入地角调整示意图Fig.12 Adjustment of contact angle of foot when robot walks on a slope with trot gait
如图12左所示,四足机器人在平坦地面上,通过前后侧腿足端入地角的调整使机器人质心投影点在支撑区域内的位置发生了改变,其相对支撑区域对角线交点O前移了S2,移动到O1点上.同样,四足机器人在斜坡地形上也可以通过调整足端入地角方式来实现机器人质心投影点的移动以提高运动稳定性,如图12右所示.其中,β为斜面坡度,h为机器人质心相对斜坡高度,O点为机器人足端支撑区域的对角线交点,O1点为机器人质心在水平支撑区域的投影点,O2点为O3点在水平支撑区域的投影点,O3点为机器人质心在斜坡上的投影点,S1为O1和O2两点之间的距离,S2为O和O2两点之间的距离.在图12左中,可通过机器人足端在机器人载体坐标系中的坐标计算出S2的值.在图12右中,通过几何关系可以得到S1的计算公式:S1htanβcosβ.四足机器人trot步态前行或上下坡时,只要其零力矩点落在稳定区域内,即可保证机器人的运动稳定.故若可保证0 ≤|S1−S2|≤r,其中r是稳定阈值,可由经验设定,则可保证机器人质心投影落在水平支撑区域对角线交点附近.如此便可通过调整机器人足端入地角来移动机器人质心投影点在水平支撑区域的位置,实现在斜坡上稳定行走的目的,虽然改方法一定程度上限制了足端的工作空间,使前后侧腿足端工作空间变小,但只要满足步态参数要求,且还可以通过足端入地角的改变实时调整足端工作空间,就能使四足机器人在斜面上稳定行走.
在仿真参数表3的基础上,搭建斜坡地面坡度β12◦,设定前侧两腿的θ5030◦,后侧两腿的θ5050◦进行四足机器人斜坡trot步态行走仿真,如图13所示.可以看出,四足机器人前后侧腿的入地角度明显不同,且能在斜坡上稳定行走.
因为四足机器人在走斜坡地形时对其前后侧腿的足端入地角进行了调整,故选取其四足机器人一对角腿观察腿部各关节角度变化.右前腿(right front,RF)和左后腿(left hind,LH)的各关节角度变化如图14所示,在第1个周期(0~0.4 s),四足机器人从下蹲姿态站立起来,所有关节角度逐渐增大;在第2个周期(0.4 s~0.8 s),四足机器人进行前后侧腿足端入地角调整,可以看出右前腿和左后腿个角度的变化明显不同;前两个周期后,四足机器人各腿关节角度均随时间呈周期性变化,说明四足机器人在调整足端入地角后,支撑腿和摆动腿周期交替进行trot步态行走,且能有效保持运动稳定性,验证了该方法的可行性和有效性.
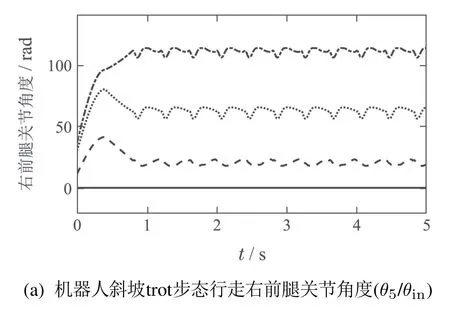
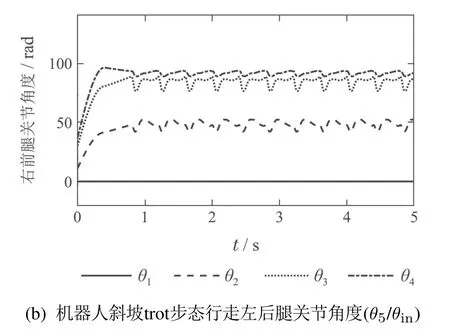
图14 扩展雅可比矩阵法机器人斜坡trot步态行走仿真右前腿关节角度(θ5/θin)Fig.14 Joint angles of right fore leg of robot in simulations of trot walking on a slope with extended Jacobian matrix method(θ5/θin)
6 实验验证
为了进一步验证所提出基于扩展雅可比矩阵的逆运动学分析方法的可行性和有效性,搭建了冗余液压驱动四足机器人实物样机,并进行梯度投影和扩展雅可比矩阵两种方法的对比实验,实验系统平台参数与表1–3一致,控制器为PC104主板.
6.1 梯度投影法
与仿真相同,取参数k−1,优化目标函数ϕ(θ)为简单的髋关节运动函数,实验结果如图15所示.

图15 梯度投影法trot行走实验Fig.15 Experiments of trot walking with gradient projection method
图16(a)给出四个周期(1.6 s~3.2 s)的四足机器人右前腿各个关节角度的变化曲线,图中:实线为机器人右前腿的给定关节角度:gθ1为外摆角度,gθ2~gθ4分别为右前腿髋关节、膝关节、踝关节俯仰角度;图中虚线为机器人右前腿的实际关节角度:tθ1~tθ4分别对应gθ1~gθ4各关节.由图可知,实际关节角度跟踪曲线与给定关节角度曲线不仅存在微小延时,而且同仿真一样,tθ2,tθ4在规律变化的同时,整体大小有微小幅度的增加,而tθ3在规律变化的同时,整体大小有较小幅度的减小.图16(b)对应给出4个周期(1.6 s~3.2 s)的四足机器人右前腿各个液压缸伸出长度的变化曲线,图中:实线为机器人右前腿各液压缸的给定伸出长度:gcy1~gcy4分别对应于给定gθ1~gθ4;图中虚线为机器人右前腿各液压缸的实际伸出长度:tcy1~tcy4分别对应gcy1~gcy4各缸.由图可知,各液压缸的伸出长度与给定伸出长度也不仅存在微小延时,而且同各关节角度变化趋势一样,tcy2,tcy4在规律变化的同时,整体大小有微小幅度的增加,而tcy3在规律变化的同时,整体大小有较小幅度的减小.以上现象表明:梯度投影法的实验结果同仿真结果保持一致,说明梯度投影法的逆运动学求解存在累计误差影响.而且,为了满足所需的控制器计算时间,程序设定的控制周期相对较长.

图16 梯度投影法trot行走实验机器人跟踪性能Fig.16 Track performance in experiments of trot walking of robot with gradient projection method
6.2 扩展雅可比矩阵法
以入地角规划式(11)为性能优化函数进行扩展雅可比矩阵法的逆运动学求解,并实验验证,结果如图17所示.

图17 扩展雅可比矩阵法trot行走实验Fig.17 Experiments of trot walking with extended Jacobian matrix method
图18(a)给出4个周期(1.6 s~3.2 s)的四足机器人右前腿各个关节角度的变化曲线,由图可知,虽然实际关节角度跟踪曲线与给定关节角度曲线存在微小延时,但还是能稳定的跟踪给定值.图18(b)对应给出四个周期(1.6 s~3.2 s)的四足机器人右前腿各个液压缸伸出长度的变化曲线,由图可知,虽然各液压缸的伸出长度与给定伸出长度存在微小延时,但还是能稳定的跟踪给定值.以上现象表明:扩展雅可比矩阵法的实验结果同仿真结果保持一致,在此验证了扩展雅可比矩阵法逆运动学求解的可行性和有效性.而且,控制器所需的计算时间较短,程序设定的控制周期也相对较短.
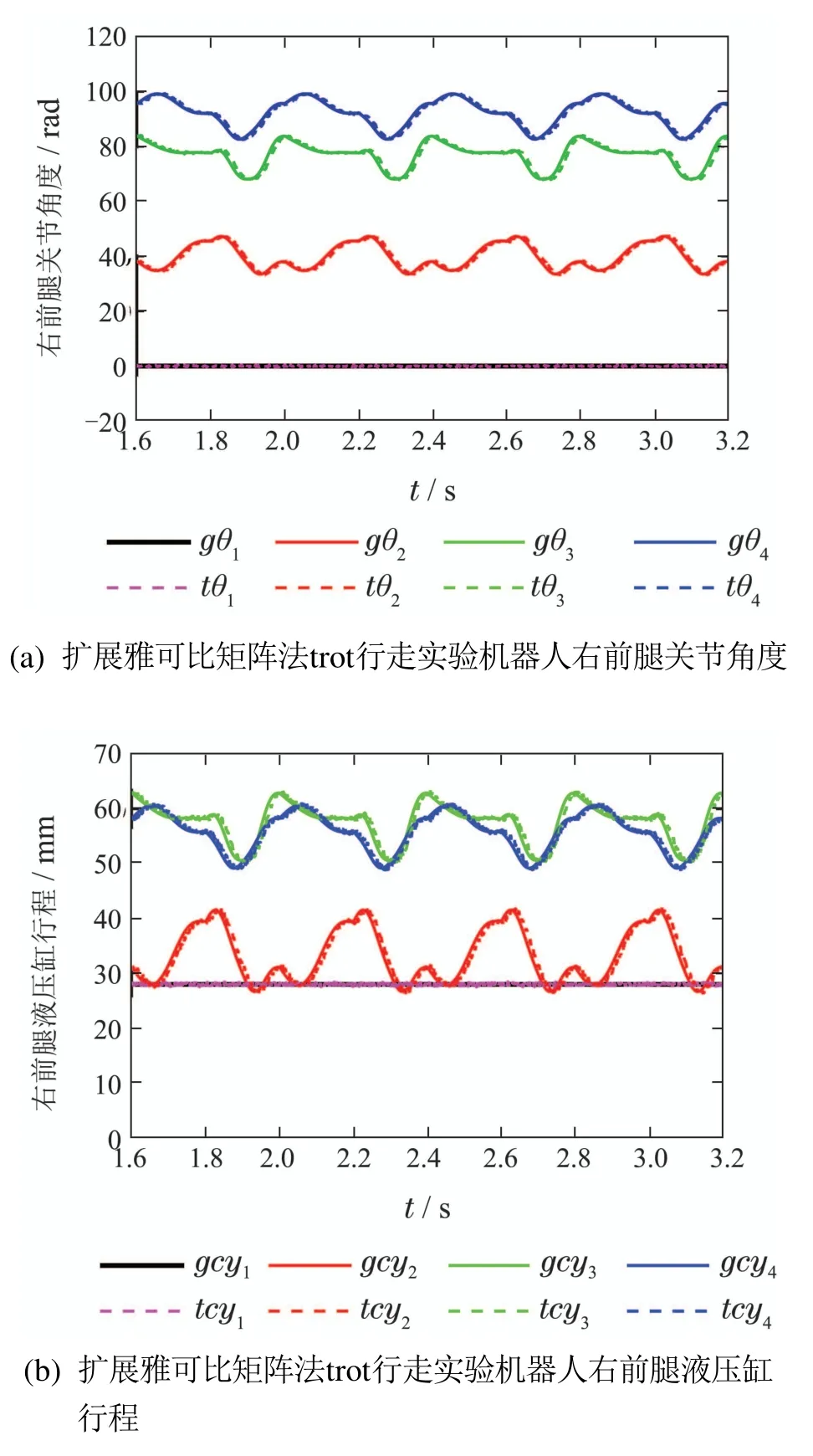
图18 扩展雅可比矩阵法trot行走实验机器人跟踪性能Fig.18 Track performance in experiments of trot walking of robot with extended Jacobian matrix method
7 结论
本文研究一种基于扩展雅可比矩阵的冗余液压驱动四足机器人逆运动学分析方法.本文的主要贡献如下:
· 给出了改进的足端轨迹规划方法以实现trot步态发生器.
· 给出了冗余液机器人逆运动学分析的两种方法:梯度投影法和本文所提出的扩展雅可比矩阵法,并进行了对比仿真.结果表明:梯度投影法存在累积误差,关节角度变化整体上存在一定幅度的偏移,且仿真速度较慢,耗时较长;扩展雅可比矩阵法则没有明显的累积误差和关节角度变化的整体偏移,且仿真速度较快,耗时较短.
· 给出了入地角度和髋关节角度的性能优化函数,并进行了仿真验证.同时利用入地角度性能优化函数仿真实现了trot步态在斜坡上的稳定行走.
· 最后通过实际样机试验对本文所提的方法进行了验证,在有负载的情况下机器人实际样机能够稳定地在trot步态下行走,证明了该方法的可行性、有效性和实际应用价值.
本文的研究可以运用到其他冗余机器人或冗余机械臂.若没有关节角度运动范围限制,出现了奇异位置,则可以通过奇异值规避方法加以解决,保证算法的一般性和可推广性.
