全息思维下的小学数学概念教学策略

潘守艳

[摘  要] “全息思维”又称“全息对应思维”，是运用全息理念认识对象客体的思维方法。把全息思维运用于小学数学概念教学，其意义在于注重引导学生对概念的全息化感知与应用，充分挖掘概念的内涵与外延，诱发学生的潜态思维，使学生对“探究→认知→应用”概念的整个过程系统化、立体化、全息化。

[关键词] 全息思维;数学概念教学;融合策略

新课程理念下的数学课堂，要求达到使学生概念清楚、形成纲目认知结构的教学目标，但当前的小学数学概念教学却存在诸多问题：有些教师只是为了“教学概念而教学”，忽视了新旧知识的联系，使得新概念的出现很突兀;有些教师忽视了对概念外延的探究，使得学生接受的新概念呈现碎片化、散点化，无法形成系统的概念模型。运用全息思维进行概念教学，有助于消除传统教学方式的弊端，大大提高概念教学效率。

一、全息思维的起源、内涵与教育应用价值

1. 思想起源

“全息”理念来自全息摄影技术，运用这种技术处理后得到的图片不再是平面影像，而是一个立体画面。全息图像处理的意义不只在于影像的“立体”化，更在于记录客体中的任意一个部分，即客体的全部过程性信息。

2. 内涵诠释

全息思维法又称全息对应思维法，是运用全息理念认识对象客体的思维方法，注重从信息相关与变异的角度认识对象客体。例如，人们常说家庭或学校是社会的缩影，说明一个社会局部包含着整个社会的信息;又如，“小数乘法的意义”“分数乘法的意义”都是“整数乘法的意义”的概念变异，但又密切相关，因为它们都具有“乘法意义”这个总概念的共同特征。教学“小数乘法的意义”“分数乘法的意义”时，都可以从“整数乘法的意义”引入，一方面有利于学生理解新概念，另一方面能让学生对“乘法意义”这条知识链有系统、全面的认知。

3. 教育应用价值

把全息思维法运用于小学数学概念教学，其意义在于引导学生由“点”到“面”，围绕一个数学概念进行教学，回顾与此概念相关的旧概念，并充分挖掘此概念的内涵与外延（变异），形成一条由各知识点（概念）组成、彼此紧密联系的知识链，使学生对“探究→认知→应用”新概念的整个过程系统化、立体化、全息化。

二、全息思维与数学概念教学的融合策略

运用全息思维法教学数学概念，能够点面结合将数学知识中的基本概念讲清楚，让学生理解透彻，促进学生抽象概括能力和实践应用能力的提升。

1. 概念引入全息化

好的开端是概念教学成功的基础。对数学概念的导入采用全息思维法，既能提高概念教学的系统性与整体性，也能使学生对新概念产生强烈的学习期待。

（1）从新旧概念衔接处引入新概念

数学是一门逻辑性很强的科学，各概念之间不是相互独立的，而是“合纵连横”、相互交融的，它们形成了严密、系统的知识链。因此，教师在概念教学过程中不应把新旧概念割裂开来，而应加强新旧概念之间的衔接与整合，从相关旧概念引入新概念，为新概念教学打好知识基础，并使学生形成严谨、周密的数学思维意识。

例如，教学“乘法的意义”时，可以先从复习加法的意义来引入。教学时可以先出示“2+2+2+2+2，3+3+3+3+3+3，4+4+4+4+4+4+4”等加法算式让学生计算，接着引导学生回顾加法的意义：“把两部分合在一起，求一共有多少，用加法计算。”然后，让学生观察上面几个加法算式并思考：“如果相同的加数很多，如‘30个7连加、50个8连加’，用加法计算方便吗？”（学生齐摇头）“那么有没有什么简便方法计算上面的连加算式呢？我们今天就来学习一种新的计算方法——乘法，大家一起寻找‘乘法的奥秘’……”

这样，由复习加法意义导入新课，巧妙地把乘法意义与加法意义衔接起来，为学习乘法的意义做好知识铺垫，让接下来的探究活动变得顺遂自然。

（2）以感性素材为铺垫引入新概念

“感性素材”是指直观化、生活化的教学资源。小学生以形象思维和感性思维为主，却不擅长抽象思维和逻辑思维，而数学概念高度抽象化，如果仅靠教师讲解学生很难真正理解与接受。因此，教师要善于把新概念与学生的已有生活经验相联系，多运用直观教具，让学生自主进行观察思考与探究交流，再归纳概括出探究对象共同的本质属性，从而完成对新概念的自主建构。

例如，学习“角的认识”时，教师可以先从学生熟悉的黑板、课本封面入手，让学生通过观察建立平面直角的概念;再让学生觀察教室相邻两面墙之间的夹角，建立两面直角概念;最后让学生观察课桌的桌面与两个侧面形成的夹角，建立三面直角概念……

黑板、课本和课桌是学生熟悉的学习用具，教室是学生熟悉的学习环境，教师利用这些生活素材引入新概念，比用教具（如三角板）导入角的概念，更具直观性与形象性，让抽象的概念变得非常具体可感。这样不仅可以消除学生对“角”的陌生感与距离感，也使学生对“角”的感知更立体、更全面、更透彻。

2. 概念感知全息化

（1）立体感知，让学生参与概念推演

很多教师喜欢用教具或课件直接呈现新概念，这种教学法的弊端是学生始终游离在概念“光圈”之外，他们对新概念的感知是被动的、浅显的，不能真正理解新概念的内涵。因此，教师要转变教学观念，变单向填鸭式讲授为师生双向互动的推演。

例如，《分米与毫米》一课主要让学生初步建立对长度单位“分米”“毫米”的认知。教学时，笔者先引导学生认识分米，让学生分别测量小棒和绳子的长度并记下数据：小棒长10厘米;绳子长1米。然后，让学生用手“搾量”（大拇指到中指之间的长度为“1搾”）一下小棒和绳子，学生搾量后发现小棒大约是1搾，绳子大约是10搾。笔者让学生思考：“如果刚才测量时一搾大约是1分米，那么小棒和绳子分别长几分米？”学生不假思索地齐声回答：“小棒长1分米，绳子长10分米。”笔者再继续追问“刚才你们已经量出小棒长10厘米、绳子长1米，想一想1分米是几厘米、1米是几分米？”学生思考后很快说出：1分米=10厘米、1米=10分米。

（毫米概念的教学方法类同分米的概念教学过程，不再赘述。）

这里，笔者用生活化的教学素材（如小棒、绳子），让学生自主通过实验探究，推演出了“分米”“毫米”的长度认知，使学生对这两个长度单位的感知与理解非常透彻到位，从源头上避免了概念混淆的问题。

（2）立体沟通，串联概念起点与外延

数学概念的文字表述只是它们的“显态信息”，其实概念还有很多“潜态信息”（如概念外延）。要实现学生对数学概念中的感知全息化，教师就要善于把概念的“潜态信息”挖掘出来，使学生对概念的认知更全面、更系统。

挖掘概念潜态信息的方法有两种：一是追溯概念起点，二是利用变式拓展概念外延。

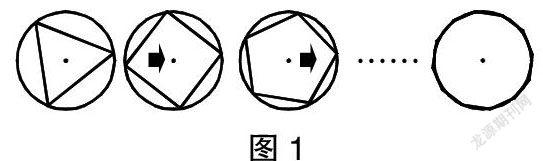
例如，教学“圆的认识”时，从表面上看“圆”与“三角形”“四边形”等图形没有任何相同之处，但如果追溯到“圆”的概念诞生起点，却与这些图形有直接关系。因此，教学时笔者用课件动态演示了从“三角形→四边形→五边形→n边形→圆”的演变过程（如图1），让学生认识到“圆不仅是由无数个点围成的封闭图形，还是由n边形演变而来的曲线图形”。这样一来既探寻到了圆的概念起点，又拓展了圆的概念外延，并且向学生渗透了数学极限思想，让学生感受到奇特的数学极限美，这对于培养学生的空间思维与极限思想有着积极的实践意义。

3. 概念应用全息化

概念应用全息化包涵两层含义：一是对概念内涵的深化理解与运用;二是对概念外延的拓展与运用（概念变异）。只有掌握了这两层含义，才能使学生完成对数学概念的正确模型思想建构。

例如，“100以内的加法和减法：连加”的巩固练习可以分为两个阶段：第一阶段加强对连加计算法则内涵的理解与运用（按照从左到右的顺序计算，先把前两个数相加，再把这两个数的和与第三个数相加）;第二阶段运用变式练习拓展连加计算法则的外延。

第一阶段巩固练习题：

23+36+27=   45+28+16=

22+28+34=   40+26+15=

出示练习题后让学生按从左到右的顺序计算，帮助学生进一步加深对100以内连加计算法则的感知与理解。

第二阶段巩固练习题：

27+12+18=  38+26+24=

46+35+25=  39+29+21=

出示练习题后先让学生按从左到右的順序计算，然后让学生观察所有算式，找出它们的共同特点。学生通过观察比较，发现每个算式后两个数相加的和是整十数。这时，教师再让学生尝试把后两个数先加，再用和与第一个数相加。学生尝试后发现这样计算非常简便，直接用口算就能求出得数。接下来教师再对连加计算法则进行补充说明：“三个数连加，按照从左到右的顺序计算，先把前两个数相加，再把这两个数的和与第三个数相加;如果后两个加数的和是整十数，可以先把后两个数相加，再用所得的和与第一个数相加。”

如此一来，教师就对“100以内连加计算法则”的概念进行了拓展与变异，使学生对概念的认知更全面，并且懂得要灵活运用法则进行计算，而不是死板地、一成不变地生搬硬套。这样，不仅提高了学生运用概念解决实际问题的能力，培养了学生的发散性思维与创新思维，而且引领学生的思维向更深、更宽的数学空间发展。

3539501908271