灰色布谷鸟搜索算法之Markov模型预测方法与应用*

冯文健

(柳州铁道职业技术学院,广西 柳州 545616)

0 引言

时间序列预测是系统建模中重要且研究广泛的课题，在现实生活中，时间序列通常是由一个随机过程产生，该过程常用于时间序列数据的建模。概率统计通常用于处理这类数据，它需要大量的数据，因此在处理有限的数据时很难得到准确的结果。灰色模型(Grey Model，GM(1,1))是邓聚龙[1]教授提出的，主要用来解决数据有限的不确定问题，适合少样本且单调性数据。传统的模型预测精度较低、误差较大。如何进一步提高预测精度是研究者感兴趣，同时也是最困难的问题。不少研究者对GM(1,1)模型进行改进，如文献[2]对初始值条件进行改进提出以x(1)(n)为初始条件的GM模型；文献[3]提出基于粒子群算法的变权累加生成的GM模型提高了预测精度；文献[4] 提出基于反向累加灰色模型的铅酸电池剩余容量预测；文献[5，6]用粒子群算法优化灰色模型的参数a和b提高预测精度；文献[7，8]从模型背景值的构造式出发改进GM模型优化算法及应用；文献[9-11]将GM模型与Markov模型结合提高预测精度。

上述文献在不同程度上提高了预测精度，但很少同时考虑参数a、b和初始值s的选择对灰色系统的影响，又回避了背景值的构造，本研究提出一种灰色布谷鸟搜索算法直接计算参数a、b和初始值s，然后利用GM(1,1)模型预测，最后用Markov模型修正预测值以此提高精度。

1 基础研究

1.1 原始的GM(1,1)模型

传统的GM(1,1)预测模型描述如下：

1)假定非负的原始数据序列为x(0)={x(0)(1),x(0)(2),…,x(0)(n)}，在其序列上的一阶累加生成算子:

(1)

2)z(1)={z(1)(k)}为x(1)(k)的紧邻均值序列:

z(1)(k)=λx(1)(k-1)+(1-λ)x(1)(k),λ∈[0,1]

(2)

3)假定x(1)近似呈指数变化，GM(1,1)模型的白化方程可以表示为：

(3)

4)通过离散式(3)，得到灰色微分方程为：

x(0)(k)+az(1)(k)=b

(4)

5)采用最小二乘法计算参数a和b，

A=(BTB)-1BTYn

(5)

式(5)中，A，B和Yn表达式为：

6)通过式(6) 计算GM(1,1)的时间响应方程：

(6)

7)原始数据的恢复值由式(7) 方程给出：

(7)

1.2 布谷鸟搜索算法

布谷鸟搜索算法(Cuckoo Search algorithm，CS)是由英国剑桥大学YANG Xin-she于2009年提出[12]，该算法模拟了布谷鸟寻窝产卵的过程，其位置更新式为：

(8)

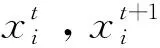
2 改进方法

已有的研究表明，GM(1,1)模型的预测精度取决于参数a和b的取值及初始条件s的选择，因此，如果选择合适的参数和初始值是提高系统性能的关键。本研究采用布谷鸟搜索算法计算a、b和s的值。

2.1 种群编码

nest=[si,ai,bi],i=1,2,…,n

(9)

nest表示鸟巢空间，si表示初始值，ai表示发展系数，bi表示灰作用量

2.2 目标函数

(10)

式(10)中，S2为原始数据、S1为残差的均方差，将C值最小值作为目标函数。

2.3 灰色布谷鸟搜索算法(CS_GM)

1)读取原始数据序列，确定参数a、b和初始值的范围区间。

2)在指定的区间内随机初始化种群，生成n个鸟巢可以作为问题的候选解，每一个鸟巢的编码按式(9)产生。

3)利用式(10)计算每一个鸟巢的目标函数值，并记录最优值fmin和最优解best。

4)开始循环迭代，运用式(8)求解参数a、b和初始值，并记录最优值fnew和最优解bestnest，若fnew

5)判断循环是否结束，若结束输出最优解best，否则跳转至4)。

7)利用式(7)还原原序列，得到预测数据。

2.4 CS_GM _Markov模型

Markov模型是一种比较简单的随机过程。该过程是研究一个系统的状况及其转移的理论。它通过对不同状态的初始概率以及状态之间的转移概率的研究来确定状态的变化趋势，从而达到对未来进行预测的目的。CS_GM_Markov计算步骤如下：

2)计算状态转移概率矩阵：

(11)

mij表示从状态Ei转移到状态Ej的次数，Mij表示状态Ei出现的次数。

3)计算初始概率v0， 则第t时刻状态概率为：

vt=v0×pt=[v1,v2,…,vn]

(12)

4)Markov模型的预测值为：

(13)

式(12)中的Ai，Bi分别表示状态Ei区间的边界值。

3 仿真实验与分析

实验数据选自2015年郑州市8月份的地铁闸机刷卡数据， 以8月1-7日的10个站为测试点，预测8月8-10日各站的客流量，原始数据见表1。

表1 8月1-10日的各站点数据

表1的“8-1”表示8月1日，其余依次类推。在Matlab R2010a环境下分别仿真实验GM(1,1)，CS_GM和CS_GM_Markov预测模型。实验中的参数设置为：种群规模n=25；初始值s和灰作用量b的范围为[min(x(1))，max(x(1))]，发展系数a的范围为[-0.5，0.5]，迭代次数为100。

为比较本研究改进方法的优越性，选用式(14)对预测结果进行误差评判。

(14)

GM(1,1)和CS_GM 2种算法仿真结果见表2。

表2 GM预测与CS_GM预测结果比较

由表2可知， GM(1,1)预测8月8日至10日的MAP值分别为：11.5582392，22.20145，8.7756069；CS_GM预测8月8日至10日的MAP值分别为：8.6228，15.9962，5.2581，显然CS_GM预测误差更小，说明结果更精确，另外，从表2和表3可知，CS_GM预测未来3天的结果更接近于真实值，可见改进CS_GM预测模型效果更好。

为进一步提高预测结果,再采用Markov模型对CS_GM预测结果进行修正，对121站点进行Markov模型修正，见表3。将预测值/实际值划分为3种状态，其区间分别：(97%，99.3%)，(99.3%，101.6%)，(101.6%，103.9%)，计算其状态转移概率矩阵：

因8-7处于第一状态，所以其初始为v0=[1，0，0]，则v1=v0×p1=[0，0，1]，则8-8的修正值为：22216.506×0.5[(1.016+1.039)]=22827.46，同理可以计算8-9，8-10的Markov修正值分别为：22316.48，22571.97。仿照相同的方法可以依次计算其他站点的Markov修正值，最后结果见表4。从表4可知，CS_GM_Markov修正8月8日至10日的MAP值分别为：8.1914，14.6814，2.4551，均小于CS_GM的MAP值，从整体上说明CS_GM_Markov修正的预测值优于CS_GM预测值。3种模型求解的预测值与真实值的拟合图(图1至图3)，相对误差比较图(图4至图6)。由图1至图3可知，CS_GM和CS_GM_ Markov模型预测结果与实际客流量拟合度较好且均优于传统的GM(1,1)模型，CS_GM_ Markov模型的优越性从图1至图3不太明显，但从图4至图6可知，对大部分站点来说CS_GM_ Markov的相对误差更小，比如图6共有10个站点，其中有7个站点的CS_GM_ Markov误差均小于CS_GM误差；其中有9个站点的CS_GM_ Markov误差均小于GM误差。因此，所有的实验表明本研究所提出的改进混合预测模型明显优于传统的GM(1,1)模型。

表3 121站点CS_GM预测结果状态划分

表4 各站点CS_GM_Markov修正值

图1 8月8日不同模型各站点预测值

图2 8月9日不同模型各站点预测值 图3 8月10日不同模型各站点预测值

图4 8月8日不同模型各站点相对误差 图5 8月9日不同模型各站点相对误差

图6 8月10日不同模型各站点相对误差

5 结 语

本研究结合灰色理论与布谷鸟搜索算法建立了灰色布谷鸟搜索预测模型，在此基础上再利用Markov模型进行修正，进一步提高了预测精度。将此组合模型应用于郑州市地铁10个站点的实验仿真分析表明，本研究提出的预测模型的预测精度明显高于传统的灰色模型，能较准备的预测地铁各站点的日客流量，为地铁交通系统的预警提高科学的基础依据。但在利用Markov模型修正时，状态的个数是随机划分的，预测结果会随着区间值的不同而发生细微的变化。如何更好地改善预测方法，提高预测精度是进一步研究方向。