刚柔耦合空间闭链机器人轨迹跟踪与振动抑制研究

张青云 赵新华,2 刘 凉 戴腾达

(1.天津理工大学计算机科学与工程学院， 天津 300384；2.天津理工大学天津市先进机电系统设计与智能控制重点实验室， 天津 300384；3.天津理工大学机电工程国家级实验教学示范中心， 天津 300384)

0 引言

柔性机器人具有轻质、高精度、快速响应等特点，广泛应用于航天、设备制造、工业设计等领域[1-4]。相对柔性串联机器人而言，柔性闭链机器人能增加有效载荷、减少累积误差、提高工作效率[5-8]。因此，柔性闭链机器人动力学分析及控制策略研究已成为热点问题。刚柔耦合机器人具有强耦合、高度非线性特性，大部分学者先采用奇异摄动法将刚柔耦合机器人进行降阶，分解为快变和慢变子系统后再进行控制策略研究[9-11]。文献[12]针对慢变子系统采用自适应鲁棒终端滑模控制，而对快变系统则通过自适应状态观测器的最优控制来抑制振动。文献[13]根据Schur分解法，提出基于时间尺度设计的状态变量特征值控制器。文献[14]通过加速度反馈控制算法有效抑制了平面3-RRR柔性并联机器人的自激振动。文献[15]通过设计一种新的自适应滑模控制器来研究一类时滞空间机械臂的控制问题。文献[16]根据非奇异快速终端滑模面和多幂次趋近律，提出了一种带扰动补偿的控制律。对于多变量、高纬度的刚柔耦合机器人，奇异摄动法虽然能对模型进行降阶，但同时也增加了子系统的复杂程度，使控制方案的实时性降低、轨迹跟踪精度不能得到有效提高。因此，文献[17]基于径向基神经网络设计了逼近控制算法，对并联机器人运动轨迹进行跟踪。文献[18]基于反馈线性化控制策略对机械臂的末端轨迹进行跟踪。

目前，对含柔性关节或柔性连杆的控制分析主要以空间机械臂、串联机器人及平面并联机器人为研究对象[19-24]，鲜有对高维度、多变量的空间刚柔耦合并联机器人的轨迹跟踪和振动抑制问题进行研究。本文以含空间柔性构件的刚柔耦合闭链机器人为研究对象，采用有限元法对空间柔性构件进行离散，基于浮动坐标系描述柔性构件的位移场矢量，最后通过Lagrange方程建立考虑末端执行器微小位移的动力学方程。利用基于前馈补偿的PD控制算法对末端执行器轨迹进行跟踪，以消除柔性构件变形产生的振动。

1 刚柔耦合空间闭链机器人动力学模型

1.1 系统分析模型

考虑系统中含有空间柔性构件的闭链机器人作研究对象，其结构示意图如图1所示。

由图1可知，从动杆的转动轴线垂直于驱动杆和中间连杆的转动轴线，在全局坐标系下需看作空间构件。且其长径比(即连杆长度与直径的比值)大于20，当系统高速运行时，其产生的弹性变形不可忽略。因此，本文将从动杆作为空间柔性构件来建立其动力学模型和分析其轨迹跟踪性能会更符合实际工况。

刚柔耦合空间闭链机器人中的3条运动支链呈三角对称分布，因此，通过建立任意一条运动支链的分析模型即可获得其他运动支链的动力学特性，其分析模型如图2所示。

根据图2可得，全局坐标系OXYZ和局部坐标系Pxyz分别设在静平台和刚性末端执行器的几何中心，各构件坐标系分别设在上关节处，并且在柔性空间变形的影响下，刚性末端执行器将产生微小位移，其变化后的坐标系为P′x′y′z′。为了简化空间柔性连杆在全局坐标系下的绝对运动描述，将浮动坐标系原点设在构件端点Ci(i=1、2、3)处，则空间柔性构件相当于一个悬臂梁，从而消除了相对运动中刚体的运动模式。端点Ai、Bi、Ci为转动关节(R副)连接处，Pi为虎克铰(U副)连接处，li和mi分别为构件长度和质量，θi1、θi2、θi3为构件与转轴之间的刚性转角，其中i=1，2，3。刚性末端执行器端点Pi在微小位移作用下将变到P′i的位置，其将坐标系P′x′y′z′变换到Pxyz的变换关系可表示为

(1)

式中ε——末端执行器微小转角

ΔxP、ΔyP、ΔzP——末端执行器微小位移

而由局部坐标系Pxyz变换到全局坐标系OXYZ的变换矩阵为

(2)

式中φi——驱动构件坐标系与全局坐标系之间的夹角

1.2 运动学方程

空间柔性构件上任意点w在全局坐标系下的位移场矢量可通过浮动坐标系表示为

(3)

其中

式中r0——浮动坐标系原点在全局坐标系下的位移矢量

rw——空间柔性构件上任意点w在全局坐标系下的位移场矢量

T——浮动坐标系到全局坐标系的变换矩阵

u0、uf——空间柔性构件在浮动坐标系下的未变形矢量和变形矢量

qf——单元节点位移矢量

N——单元形函数

NA、NB、NC——插值向量

同时，空间柔性连杆在全局坐标系下的绝对角速度为

(4)

刚柔耦合空间闭链机器人的运动支链几何约束关系为

lAiBi+lBiCi+lCiPi=lAiO+lOPi

(5)

其中

式中P——刚性末端执行器在全局坐标系下的理想轨迹

r、R——末端执行器和静平台半径

l1、l2——驱动杆和中间连杆长度

对式(6)用高斯消元法进行求解即可得系统理想轨迹与驱动构件之间的函数关系。

1.3 动力学方程

由动能公式可得系统各构件动能为

(6)

式中vi1、vi2——驱动杆和中间连杆的速度矢量

ωi2——中间连杆角速度矢量

J2——中间连杆转动惯量

ρ——空间柔性构件密度

l3——空间柔性构件杆长

V——空间柔性构件体积

Jc——空间柔性构件转动惯量

同理，系统中各构件势能为

(7)

式中A——柔性构件横截面面积

E——柔性单元弹性模量

G——剪切模量

Iyy、Izz——空间柔性构件横截面对y轴和z轴的惯性矩

Ip——柔性构件横截面对x轴的极惯性矩

ψx——绕x轴的弹性转角函数

考虑刚性末端执行器在空间柔性连杆弹性变形下引起的微小位移，则其动能和势能表达式为

(8)

其中

P′=P+JPΔP

式中mP——末端执行器质量

J——转动惯量

ωP——绝对角速度

zP′——全局坐标系Z轴方向位移

JP——系统的协调矩阵[25]

ΔP——微小位移

将式(8)中的动能和势能进行装配即可得系统总动能T和总势能V，再将其代入Lagrange方程可得

(9)

其中

式中qj——系统广义坐标

τj——系统广义力

j——广义坐标数

将式(9)简化可得系统动力学方程为

(10)

式中M——系统惯性质量矩阵，M∈R45×45

K——刚度矩阵，K∈R45×45

C——包含科氏力、离心力的矩阵，C∈R45×45

τ——控制系统及驱动力矩组成的列向量，τ∈R45×1

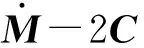
2 基于前馈补偿的主动振动控制方法

刚柔耦合空间闭链机器人是一个多变量、强耦合、时变的高维度非线性系统，为了避免通过系统分解进行模型降阶导致的控制器叠加、控制参数复杂等不足，直接基于考虑空间柔性构件变形及刚性末端执行器产生微小位移的精确动力学模型，将预先求出的控制力矩对系统进行前馈补偿，提高系统响应速度和跟踪性能。再与反馈PD控制器相结合，消除关节的转角偏差、抑制空间柔性构件振动，从而改善系统性能，其轨迹跟踪控制框图如图3所示。

2.1 控制律设计

刚柔耦合空间闭链机器人的轨迹误差为

(11)

通过建立的约束关系式(5)即可获得系统驱动关节角位移、角速度及角加速度。

反馈PD控制器为

(12)

式中，kp∈R3×1、kd∈R3×1。

2.2 前馈控制

(13)

将式(12)和式(13)进行组合即可得到系统基于前馈补偿的控制算法为

τ=τf+τd

(14)

3 数值分析

基于图1的刚柔耦合空间闭链机器人进行数值分析，其结构参数如表1所示。

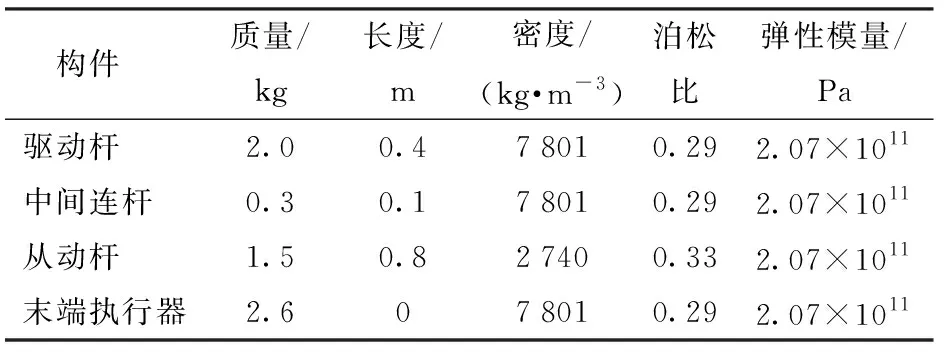
表1 系统结构参数Tab.1 System parameters

由于控制模型是基于动力学模型建立的，为了验证控制模型的有效性，需先保证推导动力学模型的正确性。首先，采用Matlab对上述推导的动力学方程进行编程求解，再与ADAMS和Simulink联合仿真的动力学模型的解进行对比，联合仿真框图如图4所示。

设末端执行器理想轨迹为

(15)

式中，末端执行器角速度ω=2 rad/s，t=5 s，时间间隔为0.005 s，则理论模型和仿真模型对比结果如图5所示。

由图5可知，仿真模型驱动力矩大于理论模型，是由于仿真模型存在建模误差、曲线拟合误差及关节间隙等，但理论模型和仿真模型各支链驱动力矩运动趋势一致，验证了推导的动力学模型的正确性。由于理论模型在求解过程中没有对多解进行筛选，导致力矩图中存在突变现象，也将为控制算法的修改提供指导。因此，基于推导的动力学模型进行控制器设计将简化设计过程，且结果更精确。

为了验证控制器的有效性，通过对比末端在不同载荷作用下的轨迹跟踪精度、空间柔性构件的振动抑制情况及相对位置PID控制算法的控制效果来进行说明。

通过参数整定得到系统控制参数为

(16)

将式(16)、(14)代入式(10)，即可得到控制算法作用下的刚柔耦合空间闭链机器人刚性末端执行器的实际轨迹。图6分别为末端载荷为自由状态、1倍臂杆质量及5倍臂杆质量的刚柔耦合空间闭链机器人末端执行器在X方向、Y方向及Z方向的轨迹跟踪曲线。

由图6可知，系统先到达无控实际轨迹，即系统基于建立的刚柔耦合动力学方程(11)直接计算出含柔性变形的实际振动轨迹，然后在控制算法作用下振动逐渐减小，最后趋于一个稳定值。对于不同末端载荷作用下的跟踪轨迹，只要对控制参数进行合理调整即可让末端轨迹在短时间达到平衡，保证了大范围刚性运动精确性。

由于柔性构件产生的弹性振动对系统末端轨迹精度具有重要影响，因此，所提控制器是否有效还需对柔性臂杆在控制器作用下的弹性振动进行分析。图7为有无控制器作用下柔性构件轨迹对比曲线。

图7a、7b为空间柔性连杆在X和Y方向的轨迹跟踪曲线。其中，系统无控制器作用的轨迹振动均大于有控制器作用的轨迹曲线，验证了控制器能有效抑制系统柔性变形产生的振动。由于系统刚性末端执行器的理想轨迹为Z平面的圆形轨迹，其无控作用下的轨迹也趋于一条直线，但当空间柔性构件质心与静平台质心之间的相对距离最大时，构件将产生较大波动，而在控制器作用下其能快速到达平衡位置，消弱了柔性振动。

为更加直观地分析所提控制器的有效性，将本文控制方法与位置PID 控制方法进行对比，其结果如图8所示。

由图8可知，本文控制方法作用下的轨迹精度高于位置PID控制方法，是因为本文控制方法是基于精确动力学模型而进行设计，并且考虑了系统在运动过程中的动态特性，所以既保证了轨迹精度，又抑制了弹性振动。

为了更直观观察不同控制器的控制效果，对比了不同控制方法下的跟踪轨迹最大误差，其结果如表2所示。

表2 误差分析Tab.2 Analysis of errors mm

由表2可知，末端执行器跟踪轨迹在本文控制器作用下X方向上位置误差相对位置PID方法降低了89.7%，在Y方向位置误差降低了4.3%，而在Z方向位置误差降低了12.9%，保证了末端执行器轨迹跟踪精度。

因此，基于前馈补偿的反馈PD控制算法既能更好地跟踪轨迹又能抑制柔性变形产生的振动。

4 结论

(1)基于浮动坐标系对经有限元法离散后的空间柔性构件位移场矢量进行描述，再通过矢量闭环法建立运动支链约束关系，由此得到刚柔耦合空间闭链机器人各关节与末端执行器的函数关系，为前馈补偿提供含有耦合项的理想关节角位移、角速度及角加速度曲线。

(2)根据末端执行器在空间柔性构件变形下引起的微小位移，建立了考虑刚性末端执行器微小位移的动力学模型，提高建模精确性，减少控制器干扰因素。

(3)通过前馈补偿对轨迹进行跟踪与反馈PD控制律改善模型跟踪性能的复合控制方式对刚柔耦合空间闭链机器人进行控制，并通过仿真验证了控制算法的有效性。

(4)由数值分析可知，选择合适的控制参数即可对系统进行轨迹跟踪。空间柔性构件的弹性变形对系统的动态特性及轨迹精度具有重要影响，可通过主动抑制振动来保证系统的稳定性和准确性。