刚柔耦合串联机械臂末端位置误差分析与补偿

2021-03-20谭月胜詹登辉张彭豪

农业机械学报 2021年2期

谭月胜詹登辉张彭豪

(北京林业大学工学院，北京 100083)

0 引言

工业机械臂自身结构参数误差及柔性误差均会导致其末端执行器的实际位置发生偏离，从而使机械臂绝对定位精度降低[1]。因此对其进行误差分析与补偿显得尤为重要。国内外研究者对提高机械臂末端运动精度进行了大量研究。陈宵燕等[2]对串联机器人多模式标定及误差补偿方法进行了相关研究，建立了包含几何和柔性的误差模型，利用线性递减权重的粒子群算法选取测量位姿，提出了一种局部补偿方法，同时制定了一种多模式精度提高策略。TAN等[3]利用压缩感知法对串联机械臂的几何误差进行了补偿。LIU等[4]利用七次多项式与粒子群算法，并结合对机械臂关节进行轨迹规划，减小了机械臂末端的综合误差。机械臂作为一个强耦合性系统，其连杆和关节的弹性变形及动载荷等对末端执行器位置精度的影响均不可忽略，而采用运动学标定方法减小因柔性产生的误差时，效果不佳。针对机械臂刚柔耦合的情况，VOLECH等[5]在机器人的减速器和连杆存在柔性时以仿真方式获得了机器人末端的形变量，以输入整形法对机器人末端误差进行了补偿。考虑到机械臂对于快速响应的要求，吴昊等[6]提出一种连续线性化模型预测控制方法来提高柔性空间机械臂的末端轨迹精度。由于机械臂柔性造成的非线性误差不可忽略，因此可结合上述方法针对具体的研究对象设计相应的补偿策略，对机械臂末端位置误差进行补偿。

本文针对机械臂因连杆与关节柔性变形而引起的末端位置的非线性误差问题，分析其误差变化情况，并对误差进行补偿。首先，建立刚柔耦合机械臂动力学和关节偏差相结合的误差模型；其次，利用有限元法与软件仿真[7-9]分析末端执行器位置误差变化；最后，基于Matlab并结合实际应用提出一种快速补偿方法，对机械臂末端位置误差进行离线补偿及实验验证，以期提高机械臂末端位置精度。

1 刚柔耦合机械臂误差模型及数值仿真

1.1 IRB1410型机械臂动力学误差模型

IRB1410型机械臂结构如图1所示，其本体结构包括：基座、腰部、大臂、肩部、小臂、腕部及法兰盘，作为一款六自由度机械臂，因其前3个关节及连杆对末端位置精度的影响远大于后3个关节及连杆，故将大臂连杆、小臂横杆和大臂平行的拉杆等效为Euler-Bernoulli梁模型研究其柔性变形，利用混合坐标系法和假设模态法来描述机械臂柔性杆的弹性变形[10-11]，并将关节等效为线性扭簧[12]，按照图1的尺寸参数可得简化模型如图2所示，其中用惯性坐标XiYiZi(i=0,1,2,3)描述刚体的运动，柔性杆件的弹性变形则用固连在其根部的浮动坐标xjyjzj(i=1,2,3)表示。

对图2中柔性杆上任一点在基坐标系X0Y0Z0下的位置关系可表述为

ri=Ai(ui+vi+li-1+li-2+R)

(1)

(2)

(3)

式中R——原点O1指向O2的矢量

li——杆i在自身惯性坐标系下的位置矢量，规定l0为零向量

ui——柔性杆在该任意点处未变形时的位置向量，i=2,3

vi——柔性杆在该任意点处产生变形后的位置向量，i=2,3

a1、a2——前两阶模态坐标

Ai——任意时刻时该浮动坐标系在基坐标系下的坐标变换矩阵，i=1,2,3

θ1——任意时刻回转角

θi——关节i转动角，i=2,3

因此，该点的速度为

(4)

则柔性杆动能为

(5)

柔性关节动能为

(6)

其中

Ji=JriN2(i=1,2,3)

式中Ji——被驱动的机械负载转动惯量

N——被驱动的机械负载质量

Jri——第i关节电机转子转动惯量，i=1,2,3

在机械臂简化模型中，将其腕关节及末端的负载视为依附于第3连杆末端的质点，质量为mg，则负载动能为

(7)

式中l2——大臂杆长l3——小臂杆长

综上所述，机械臂系统的总动能可表示为

T=Tl+Tr+TG

机械臂系统的势能包括杆件的弹性势能与重力势能以及柔性关节的弹性势能，柔性杆弹性势能为

(8)

式中Ei——柔性杆弹性模量

Ii——柔性杆截面惯性矩

重力势能为

(9)

柔性关节弹性势能为

(10)

式中kti——第i关节的扭转刚度，i=1,2,3

则系统总势能为

U=Ul+G+Ur

根据第二类拉格朗日法公式有

(11)

其中L=T-U，由式(5)～(10)可得机械臂的动力学模型为

(12)

(13)

其中

q=[θ1θ2θ3a1a2b1b2θ4θ5θ6]T

式中q——广义坐标向量

QF——广义外力二次项组成所对应的广义力

Qr——广义速度二次项组成所对应的广义力

K——刚度矩阵

M——质量矩阵

J——JriN2组成的向量

Δθ——关节角偏差

由于机械臂在各连杆自身重力和附加载荷的影响下，关节轴线会受到力矩的作用，从而导致关节发生微小位移，产生一定的转角偏差。在将柔性关节等效为扭簧模型时，关节角偏差与关节所受力矩的关系可以表示为

Δθ=Cτ

(14)

式中C——柔度系数，rad/(N·m)

τ——力矩，N·m

对于 6 自由度串联式机械臂，其前3个关节产生的关节转角偏差对末端定位精度的影响高于后3个关节[13-14]，为简化计算模型，只对前3个关节作柔性化处理和误差建模分析。图3为简化模型的误差分析图，建模时暂且不考虑连杆的微小变形，在机械臂运动过程中，考虑惯性力矩的影响，将其当成平衡力系研究，由此可得大臂自重、小臂自重和负载对第2、3关节轴线的力臂为

(15)

式中lc2——大臂重心到关节旋转轴线的距离

lc3——小臂重心到关节旋转轴线的距离

则第1、2、3关节力矩为

(16)

式中F1——大臂自重F2——小臂自重

FG——负载载荷

m1、m2、m3、mG——杆1、2、3及负载质量

r——杆1回转半径，与图2中的R相等

结合式(14)，并设m=F2/F1，n=C3/C2，C1、C2、C3分别表示第1、2、3关节的柔度系数，可得第1、2、3关节处的关节角偏差为

(17)

1.2 机械臂动力学模型数值仿真

关节力矩是各关节转动惯量与其角加速度的乘积，广义力矩给定为其关节力矩的两倍，因此设定各个关节与时间的角位移为

(18)

结合式(12)、(13)、(17)，同时给出数值仿真参数：l1=0.375 m，l2=0.72 m，l3=0.89 m，R=0.15 m，EI2=4.09×102N·m2，EI3=2.33×102N·m2，m1=87.49 kg，m2=42.26 kg，mg=11 kg，kt1=6.48×106N·m/(°)，kt2=1.492×106N·m/(°)，kt3=6.08×105N·m/(°)，t=2 s，Δt=0.04 s，C1=3.356×10-10rad/(N·m)，C2=6.948×10-10rad/(N·m)，m=0.7，n=1.4，采用Newmark β法[15]计算得到机械臂末端3个方向误差变化曲线，如图4所示。

由图4可知，机械臂末端的误差随时间变化而变化，3个方向均呈现波动性和非线性，x、y方向的误差变化范围较接近，而z方向因末端具有竖直向下的负载，故误差变化较大，因此机械臂连杆柔性与关节柔性对末端位置精度的影响不可忽略。图5是对动力学模型进行数值仿真后得到的末端综合距离误差。由图5可以看出，综合距离误差仍然处在一个较大的范围内，因此有必要对已建立的动力学模型的准确性进行验证。

2 刚柔耦合机械臂末端运动误差仿真分析

2.1 模型建立

机械臂在自重、负载以及惯性力矩的影响下，连杆与关节均会发生一定程度的柔性变形[16]。机械臂连杆由于是细长杆结构，在载荷和惯性力的作用下引起末端执行器位置发生偏离，因此仅将大臂、小臂和大臂平行的拉杆利用ANSYS软件作柔性化处理，可得含柔性杆件的机械臂三维模型，如图6所示。而将关节等效为线性扭簧的形式，并在关节处施加关节力矩函数以实现柔性化[17-18]。以基座与腰部之间的关节为例，在基座旋转轴输入端添加转动副和驱动函数，腰部输出端添加转动副和关节力矩以带动腰部旋转，柔性关节1模型如图7所示。

2.2 运动误差仿真

为与理论模型相对应，末端载荷和各关节转动规律均设置为理论建模时所给定的数值，在ADAMS中设置仿真时间为2 s，仿真时间间隔为0.004 s，仿真后再与设置相同参数的刚体模型对比。

图8、9分别为对刚柔耦合机械臂模型进行ADAMS仿真时机械臂末端3个方向的距离误差变化曲线及末端综合距离误差变化曲线，对比图4和图8可知，由于受到杆件柔性、关节柔性及负载等因素的综合影响，在一段时间内会使机械臂在运动过程中做非线性颤动；但从3个方向上分别对比数值仿真与ADAMS仿真结果可得，两种仿真所得到的3个方向上的误差变化趋势及范围基本相同。同时对比图5和图9，可得图10的结果。

由图10可得，因ADAMS仿真中所取模态阶数为20阶，高于数值仿真时的模态阶数，而模态阶数越高模型也更接近真实情况，ADAMS软件建立的刚柔耦合模型其耦合度也更强，在同样的时间周期内和运动规律下，末端颤振的频率也会较数值仿真时更高，因此两种仿真结果会有所差别，在误差允许范围内，数值仿真与ADAMS仿真的结果可以相互验证所建机械臂动力学模型及机械臂刚柔耦合系统模型的准确性。

3 末端位置误差补偿

由于机械臂中唯一可控的参数为其关节转角，因此使用算法找到合适的关节角，并对关节角进行微调，以达到误差补偿的目的，其补偿原理如图11所示[19]。

基于所得误差变化曲线具有强非线性特征，而神经网络对于无规律、非线性数据具有很好的拟合作用，它无需求出具体误差模型方程，只需对误差样本进行网络训练，便可得到所需要的误差模型[20-21]，因此利用BP算法训练、预测误差，其中输入为6关节角，输出为x、y、z3个方向误差。在ADAMS仿真界面中保持不变的转动规律，设置仿真时间为6 s，仿真时间间隔为0.02 s，可以得到301组误差数据，将其作为样本利用BP神经网络算法进行训练，可得到网络训练输出误差与仿真所得误差的对比拟合曲线，如图12所示。

由图12可得，利用BP算法对于非线性、无规律数据具有很好的拟合效果，其拟合率达99.226%，网络训练输出的误差与仿真所得误差虽有较为微小的差距，但不会对后续的补偿研究产生影响，并将已训练好的网络保存。

以上运用BP算法训练误差来近似拟合仿真误差的过程，主要是研究机械臂正常工作时末端的轨迹平稳现象，针对机械臂启动时的情形，由于末端的抖动造成机械臂在启动时发生振动现象而导致末端产生不规则的运动轨迹，表现为机械臂启动时各关节振动，造成各关节运动轨迹呈非线性特征，以下将对各关节不规则运动轨迹展开分析，计算BP训练实际误差拟合率，同时判定算法训练的有效性。

为验证BP算法对于误差训练的有效性，将机械臂刚柔耦合模型瞬时启动所得到的末端轨迹进行离散，设置仿真时间为瞬时启动时间1 s，仿真时间间隔为0.02 s，可以得到51组误差，运用式(18)计算得到各离散点关节转角，并进行测量实验，综合比较BP算法训练误差与实际测量误差及仿真误差的一致性。

由图13可看出，在机械臂启动瞬时的不规则运动轨迹，BP算法的拟合效果虽不明显，但是基本变化趋势相同，说明BP算法对于强非线性，不规则运动轨迹同样具有较好的拟合效果，在0.5 s之前误差拟合率达83.573%，0.5 s后误差拟合率达98.926%，BP算法训练输出的误差与仿真所得误差基本接近，与实验测量误差的差距也很小，说明机械臂启动瞬时的影响不可忽略，本文重点讨论机械臂平稳运行时的柔性因素的影响。

为简化研究，将第2节中利用ADAMS仿真得到的误差数据进行离散化，将其均匀离散成51个误差点。为实现快速补偿，提出基于正逆运动学的伪目标点法，其流程如图14所示。

主要步骤如下：

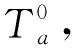
(19)

式中 IK()——逆运动学计算函数

(20)

式中f()——正运动学中关于位置点的计算函数

(3)判断实际位置点与理论位置点间的偏差E

(21)

式中E——距离误差

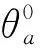
(22)

(5)通过运动学逆解求解伪逆解为

(23)

(6)基于第k次计算结果计算对应的末端位置点为

(24)

(25)

其中

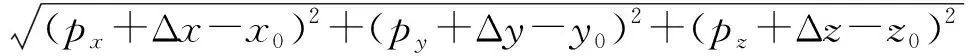
(26)

式中px、py、pz——关节转角微调后求解得到的3个方向空间的位置坐标值

Δx、Δy、Δz——神经网络训练后预测输出的3个方向误差

x0、y0、z0——期望关节角对应的末端期望位置点坐标值

将离散点结合训练的BP算法与上述计算步骤，再利用Matlab编程，根据IRB1410型机械臂设计资料设置偏差E=0.24 mm[22-23]，对所有的离散点进行计算，最终可以得到补偿前、后距离误差对比如图15所示。

由图15可知，从整体的距离误差看，利用伪目标点法补偿后，机械臂末端的位置误差均减小，能达到不错的补偿效果，其位置误差均方根减小了68.30%；在耗时方面，该方法补偿每个点的平均耗时为0.393 s，能实现快速实时补偿。

4 实验验证

4.1 末端位置点测量实验

实验以IRB1410型机械臂为研究对象进行测量，测量仪器为经纬仪，在测量前需对经纬仪进行安装调试，保证其视野清晰，显示正常，图16为调试好的经纬仪；利用贴于法兰盘处的含三角形的坐标纸测量机械臂末端位置点，如图17所示。

三角形位于机械臂末端，其相对于安装好的经纬仪坐标系原点形成一种“透视”效果，利用经纬仪测量三角形的3个顶点的水平角θ和竖直角α，可构建空间点坐标求解模型[24-25]，图18为求解模型图，三角形三顶点的坐标可分别表示为

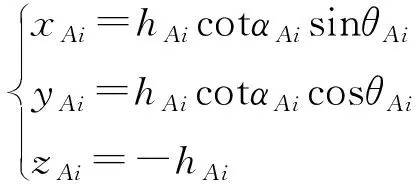
(27)

(28)

(29)

其中3个垂直距离hAi、hOi、hBi由下式计算而得

(30)

三角形边长lOA=30 mm，mOB=40 mm，nAB=50 mm。将仿真中转动规律进行离散化，将其离散成35组关节角，依次输入到机械臂示教器中，分别测量每组关节角对应的机械臂末端悬挂重物(与仿真时保持一致，为11 kg)和未悬挂重物两种位置点的水平角和竖直角，部分数值如表1所示(仅列出前5次测得数据)。

表1 挂重物前后经纬仪测量值Tab.1 Longitudinal measurements before and after hanging heavy object

根据所建立的求解模型，利用Matlab软件编程可以计算得到机械臂未挂重物和挂有重物两种情况下末端三角形三顶点的坐标值，由此可得机械臂在关节和连杆柔性变形下末端点位的位置误差。

为了验证ADAMS仿真误差与实验测量误差结果的一致性，将机械臂刚柔耦合模型仿真所得到的末端轨迹离散为25个轨迹点，相应的误差也离散为25个。表2为运用式(18)计算刚柔耦合机械臂模型在0.04、0.12、0.20、0.28、0.36 s所对应的机械臂各关节转角，以此类推计算25组关节角度(仅列出前5次输入值)。表3为刚柔耦合模型仿真的末端轨迹离散后所得25组连续时间间隔的末端轨迹误差(仅列出前5次输出值)，表4为实验阶段在连续时间间隔内点O在3个方向上的距离误差变化情况(仅列出前5次测得数据)，同时选择25组连续相同时间间隔的离散点进行对比，结果如图19所示。

表2 各关节输入转角Tab.2 Input angle of joints (°)

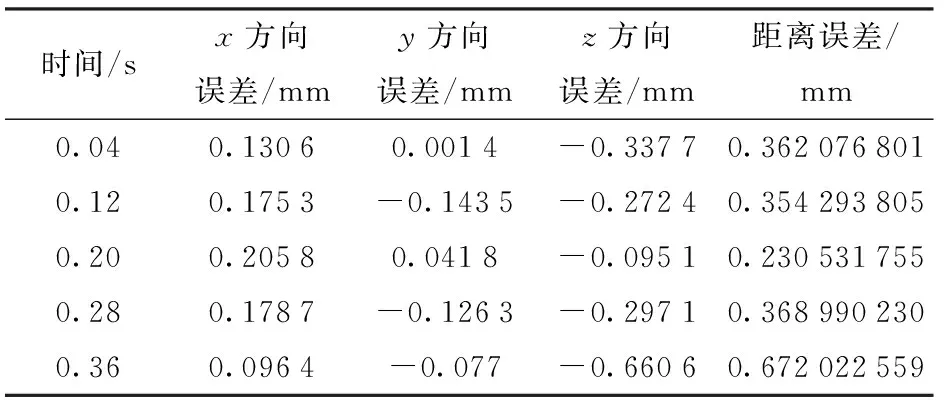
表3 离散后末端轨迹误差Tab.3 Discrete rear end trajectory error values

表4 点O 3个方向误差Tab.4 O-point three-direction error values mm

图19为数值仿真、ADAMS仿真以及实验测量的综合误差变化情况的对比曲线。由图19可看出，由于机械臂受到除柔性关节、柔性杆件及测量等因素的影响造成的运动学误差外，同时还受到机械臂的装配误差、关节驱动电机影响、机械臂启动时的末端振动等因素也会对机械臂的末端综合运动误差造成影响，造成实际综合误差大于数值仿真及ADAMS仿真时的运动学综合误差，但由于三者综合误差变化趋势基本相同，因此可利用该刚柔耦合机械臂模型来近似研究实际机械臂的运动学误差补偿问题。

4.2 末端位置误差补偿验证

为验证补偿算法的有效性和可操作性，利用所得实验数据进行误差补偿验证，因点O、A、B的误差相差不大，故选取点O作为补偿对象，图20为误差补偿流程图。考虑实验中人为和环境等因素的影响并根据IRB1410型机械臂的绝对轨迹精度，可将伪目标点法中阈值E设置为0.6 mm，补偿前后效果对比如图21所示。

由图21可看出，补偿前距离误差最大值和平均值分别为2.654、1.530 mm，补偿后距离误差最大值和平均值分别为0.538、0.299 mm，误差均方根减小了77.01%，可以验证所设计的伪目标点法对误差的补偿具有有效性，由于机械臂还受到除柔性和测量之外其他因素的影响，故机械臂的误差并未完全消除。