基于时变扰动抑制的动力换挡拖拉机起步控制方法

傅生辉 杨子涵 杜岳峰 李 臻 毛恩荣 朱忠祥

(1.中国农业大学工学院， 北京 100083； 2.中国农业大学现代农业装备优化设计北京市重点实验室， 北京 100083)

0 引言

动力换挡变速箱(Power shift transmission，PST)因换挡过程动力不中断、起步性能好、工况适应性强等特点而逐渐成为大功率拖拉机的主流配置[1]。起步控制作为PST关键技术之一，直接影响拖拉机起步性能和驾驶品质，对PST性能提升具有重要意义。

目前，PST研究多集中在液压系统仿真、换挡过程优化、换挡控制策略等方面[2-8]，对起步控制的研究相对较少。常见的车辆起步控制主要包括发动机恒转速控制和优化控制。前者简单实用，但开发效率低，工况适应性差；后者通过平衡换挡时间和滑摩等起步需求可实现车辆快速平稳起步，是当前研究的热点[9]。韩玲等[10]提出一种基于离合器执行机构鲁棒性的模型预测控制算法，可有效降低CVT (Constantly variable transmission)起步冲击度。LI等[11]设计了液体粘性传动装置(Hydro-viscous drive，HVD)，实现了拖拉机在不同意图下的平稳起步。耿国盛等[12]和周康[13]基于台架试验实现了拖拉机液压无级变速器在不同负载和起步意图下的起步控制。文献[14-16]在驾驶意图的终端约束下，采用最优控制实现了起步离合器转矩协调控制，有效保证了车辆起步品质。在试验条件和设计成本等诸多因素限制下，多领域协同仿真、机-电-液联合仿真等技术已成为拖拉机设计和性能优化的重要手段[17]。考虑起步控制的时变非线性、不确定性、工况复杂性等特点，杨阳等[18]提出了基于数据驱动的DCT车辆起步预测控制方法，通过结合发动机恒转速控制和模型预测控制算法实现了不同意图下的起步控制。GAO等[19]提出了带有建模误差观测器的线性二次型输出调节器，将扰动误差作为线性反馈控制律的派生形式，用于中型客车起步控制。

针对拖拉机起步过程建模不确定性、工况复杂多变和时变干扰等问题，本文提出一种基于高阶扰动观测器(High order disturbance observer，HDO)的动力换挡拖拉机起步控制方法。该方法在分析拖拉机起步特性基础上，利用HDO对模型的不确定性和时变扰动等进行观测，并作为线性二次型最优调节器(Linear quadratic regulator，LQR)的补偿输入，得到起步离合器的最优摩擦转矩；在文献[4]的基础上，采用无模型自适应预测控制(Model free adaptive predictive control，MFAPC)算法将控制转矩转换为离合器压力的最优轨迹，实现离合器压力的实时控制；通过Matlab/Simulink和AMESim平台构建拖拉机动力传动系统模型，分析不同起步意图和作业工况下的拖拉机起步性能，通过仿真试验验证本文方法的有效性。

1 动力换挡变速箱建模与起步过程分析

以某PST拖拉机为例进行起步过程分析，其动力学模型如图1所示。

图1中，Ie、Io、Iv分别表示发动机飞轮、PST输出轴及整机的等效转动惯量，kg·m2；Te、Tca、Tcb、Tcc、Tcd、Tv分别为发动机输出转矩，离合器A、B、C、D摩擦转矩及阻力矩，N·m；ωca、ωcb、ωcc、ωcd、ωe、ωo、ωv分别为离合器A、B、C、D以及发动机、变速箱输出轴、驱动轮角速度，rad/s；ce、co分别为发动机和PST输出轴等效旋转粘性阻尼系数；i1、i3、i4、iF、id1、iv分别为PST变速箱LL、M、H挡位、前进挡、副变速箱1挡及中央传动和最终传动的传动比。以LL挡起步为例，拖拉机通过控制湿式离合器A、B的接合过程实现平稳起步，其动力学模型可简化为

(1)

其中

(2)

式中α′——道路坡度，rad

fg——滚动阻力系数

rq——驱动轮动力半径，m

Cd——空气阻力系数

v——拖拉机行驶速度，m/s

Aair——迎风面积，m2

ρ——空气密度，kg/m3

k1——动力储备系数

kt——土壤比阻，N/m2

zt——犁铧个数

bt——单体犁铧宽度，m

ht——耕深，m

Ms——拖拉机使用质量，kg

g——重力加速度，m/s2

μ——摩擦因数

S——摩擦副有效作用面积，m2

p——摩擦副间的正压力，Pa

Δωcb——离合器B主、从件角速度差，rad/s

z1——摩擦副面数

R、r——摩擦片外、内半径，m

2 时变扰动抑制输出控制系统设计

由于拖拉机作业环境和挂载农机具类型复杂多样，受时变参数(如离合器摩擦因数、滚动阻力系数、田间坡度等)的影响，其起步过程中存在建模不确定性、参数摄动和时变扰动等问题，易造成起步冲击过大、离合器滑摩时间过长，降低拖拉机动力性和驾驶品质。因此，本文提出一种基于时变扰动抑制的LQR控制器(图2)，利用HDO估计系统的时变扰动，通过对LQR的动态补偿实现时变扰动的抑制。

2.1 线性二次型调节器设计

假设某系统为

(3)

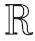
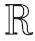
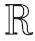
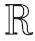
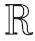
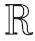
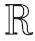
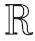
输出调节器性能泛函为

(4)

式中Q、R——正定矩阵

为求解最优控制问题，构造哈密尔顿函数

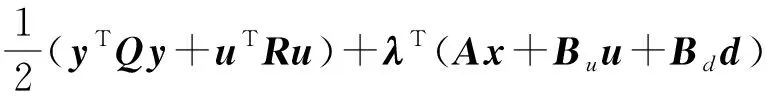
(5)

式中λ——协态矢量

由此可得

(6)

传统乘子函数λ=Px计算最优解不能有效抑制时变扰动，因此，引入包含扰动d及其各阶导数的乘子函数

(7)

式中P、hi——待定时不变系数矩阵

由式(6)和式(7)可得

(8)

其中，P由黎提卡(Riccati)方程求解

(9)

由此可得

(10)

求解式(10)可得

(11)

最终控制律为

(12)

其中

(13)

2.2 高阶扰动观测器设计

高阶扰动观测器[20]不仅能估计时间序列中的扰动信息，还可观测扰动的多阶导数，有效提高系统扰动抑制能力。假设系统中存在时变扰动d，表示为

(14)

式中di——未知常数

扰动观测器设计为

(t)=Γ0g0(t)+Γ1g1(t)+…+Γqgq(t)=

(15)

其中

(16)

Γk=diag(γk1,γk2,…,γkd)

(17)

z——高阶扰动估计参数

γij符合Routh-Hurwitz稳定，计算式为

pj(s)=sq+1+γ0jsq+…+γ(q-1)js+γqj

(18)

观测器估计误差为

(19)

多次求导后，可得

(20)

2.3 算例验证

为验证时变扰动抑制LQR控制器的有效性，利用式(3)所示算例进行时变扰动估计，其参数取值为

(21)

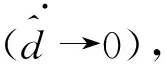
此外，引入PI观测器(Proportional integral observer，PIO)[21-22]与不同扰动导数阶次下的HDO进行观测性能对比分析。图3为HDO和PIO扰动观测结果对比，其中，HDO各阶次观测器参数为HDO0：γ0=10；HDO1：γ0=20,γ1=100；HDO2：γ0=8，γ1=15，γ2=50。

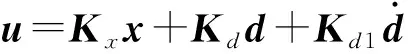
3 动力换挡拖拉机起步控制仿真分析

3.1 换挡品质评价指标

换挡品质是指在保证拖拉机动力传动系统动力性和可靠性前提下迅速、平稳换挡的程度，一般非道路车辆换挡品质最直观的评价指标为冲击度、滑摩功等[23]。

(1)冲击度

冲击度j(m/s3)指拖拉机纵向加速度的变化率。j越大，换挡平顺性越差。计算式为

(22)

(2)滑摩功

滑摩功Wfc用来衡量离合器接合过程中主动和从动件摩擦做功的大小，计算式为

(23)

式中tj——滑摩结束时间，s

Tc——离合器摩擦转矩，N·m

Δωc——离合器主、从件角速度差，rad/s

3.2 起步控制器设计

为消除动力换挡拖拉机起步控制系统的不确定性和时变扰动对起步品质造成的影响，本文将起步中时变扰动和建模不确定性集成为外部扰动项d=[d1d2]，则起步方程为

(24)

选取x1=Δωcb、x2=ωe、x3=Tcb为状态变量，u=dTcb/dt为控制变量，Te、Tv为可测扰动向量p，基于线性二次型最优控制理论，可得到起步控制系统的状态空间模型

(25)

其中

(26)

(27)

(28)

(29)

(30)

综合考虑冲击度和滑摩功计算性能泛函，最终控制律为

(31)

3.3 起步控制仿真分析

为验证本文起步控制方法的有效性，基于Matlab/Simulink与AMESim联合仿真构建了动力换挡拖拉机传动系统仿真模型，如图5所示。拖拉机主要参数如表1所示。

表1 拖拉机整机主要参数Tab.1 Parameters of tractor

选取运输、犁耕2种典型工况对不同意图下的拖拉机起步过程进行仿真分析。3种起步意图(缓慢、中等和快速)如图6所示。此外，为体现本文算法优越性，以LQR、PIO+LQR作为对照进行拖拉机起步控制仿真。其中，Q=1.3，R=1，LQR控制参数为

(32)

图7为3种起步意图(油门开度30%、60%、100%)下拖拉机运输工况起步性能仿真对比。由图7a可知，不同起步意图下，发动机转速与离合器从动盘转速同步时间为1.5～3.1 s，标志着起步离合器结束滑摩阶段进入同步阶段。油门开度越大，起步时间越短。同一意图下，PIO离合器接合速度最快。3种起步意图下，PIO接合时间分别为2.52、1.74、1.66 s，比HDO分别快3.08%、9.38%、11.23%。LQR起步时间最长，分别为3.10、2.26、2.18 s。此外，受离合器充油和MFAPC算法滞后影响[4]，在起步初期存在约0.2 s延时，对离合器接合时间产生一定影响。由图7b可知，起步初期发动机转速波动较小，但离合器摩擦转矩急剧抖动，主要原因是离合器油缸压力在初期超调引起的转矩变化[4]，其中，超调压力约0.035 MPa。由图7c、7d可知，不同起步意图下，3种方法的最大冲击度均符合相关标准要求(j≤17 m/s3)。3种起步意图下，PIO最大冲击度分别为13.49、15.69、16.85 m/s3，比LQR分别高6.81%、3.09%及8.71%，比HDO分别高29.09%、28.08%及8.71%。

图8为运输工况下观测器扰动估计值对比。由图可知，换挡初期PIO扰动估计值较大，可对扰动d进行快速补偿，虽然一定程度上增加了冲击度，但滑摩功显著降低。30%油门开度下Wfc仅15.13 kJ，比LQR、HDO分别降低9.56%、5.56%。HDO在起步初期扰动观测值较小，但其变化趋势与离合器传递转矩大致相同，得益于HDO对d的前馈补偿，3种起步意图下HDO最大冲击度分别为10.45、12.25、15.5 m/s3,冲击度控制效果最好，且能兼顾滑摩功控制需求，60%、100%油门下Wfc比LQR分别降低0.49、0.52 kJ，一定程度上减少了摩擦片滑摩，提高离合器使用寿命。

为客观评估拖拉机起步性能，本文利用试验测定的犁耕牵引力作为拖拉机机组信号进行犁耕工况下的起步仿真。其中，试验拖拉机型号为东方红LX2204型轮式拖拉机，标定功率为162 kW(图9a)，试验场为河南省洛阳市某地试验田。采集的牵引力部分数据如图9b所示。

图10为3种意图下拖拉机犁耕工况起步性能仿真结果对比。由图可知，随着负载的增加，拖拉机起步时间逐渐延长。3种方法的仿真结果变化趋势与运输工况结果基本一致。PIO起步时间最短，HDO次之，LQR起步时间最长。3种意图下HDO的转速同步时间分别为3.56、2.72、2.64 s，较运输工况分别多0.96、0.80、0.77 s。此外，由于作业机组阻力的增大和起步时间延长，3种方法的摩擦转矩在起步初期变化较小(图10b)。同一起步意图下，犁耕工况的扰动观测值也远小于运输工况(图11)。

由图10c、10d可知，虽然起步时间较短，牵引力变化并不明显，但对拖拉机起步品质仍产生较大影响。受牵引力变化影响，起步冲击度波动更剧烈，且滑摩功远大于运输作业。其中，3种起步意图下HDO最大冲击度分别为10.20、11.32、14.39 m/s3，均低于运输工况，且比PIO、LQR犁耕下的冲击度降低3.32%～22.20%。在起步过程后期，离合器油压升至系统压力，仍造成一定冲击。以犁耕下的缓慢起步为例，3种方法在此阶段的冲击度分别为10.55、11.83、10.20 m/s3，滑摩功分别为55.93、52.12、55.30 kJ。犁耕作业下PIO滑摩功仍最小，油门开度60%的滑摩功仅71.20 kJ，较HDO、LQR分别降低5.85%、5.98%。但快速起步意图下，HDO的最大冲击度为14.39 m/s3，较PIO降低12.47%，但比LQR提高4.43%；HDO滑摩功为78.82 kJ，较前两者增加6.83%、0.70%。其主要原因在于HDO建立在扰动假设模型基础上，观测器参数的设定影响了LQR对时变扰动的抑制能力。

3种方法在不同工况和起步意图下的起步品质评价指标如表2所示。HDO在一定程度上实现了拖拉机起步过程中时变干扰和建模不确定性的准确估计，通过LQR控制器能有效抑制时变扰动对起步品质的影响，显著提高了不同工况下的起步性能，且具有一定鲁棒性。

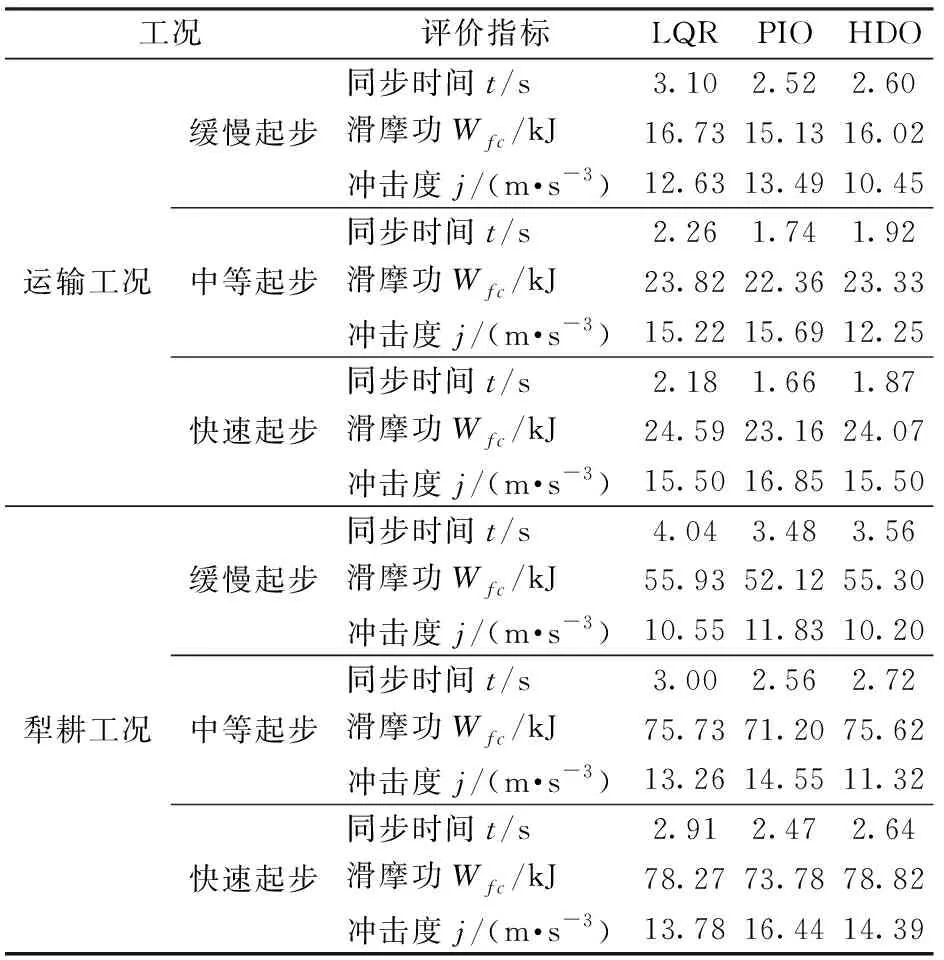
表2 不同工况下3种方法的起步仿真结果对比Tab.2 Simulation results of tractor starting up with three different methods

4 结论

(1)提出了一种基于时变扰动抑制的LQR控制器，利用HDO实现了扰动估计误差与系统状态完全解耦，可有效解决建模不确定性和外部时变扰动带来的不利影响，提高了控制系统的鲁棒性。HDO操作简单，且易于实现。

(2)依托Matlab/Simulink及AMESim联合仿真平台，构建大功率动力换挡拖拉机传动系统仿真模型，在不同作业工况和起步意图下进行了起步性能仿真分析。结果表明，HDO实现了对拖拉机起步时变扰动的有效观测，通过LQR控制器的扰动补偿控制有效降低了起步过程的冲击度和滑摩功。以中等起步为例，HDO运输工况和犁耕工况下的冲击度分别为12.25、11.32 m/s3，较PIO分别降低了21.92%、22.20%，滑摩功分别为23.33、75.62 kJ，较LQR分别降低了2.1%、0.15%，在一定程度上提高了拖拉机换挡品质，具有较好的控制鲁棒性。