步进频率随机变化的2FSK-步进频雷达通信一体化波形设计*

马启成

（海军工程大学，湖北 武汉 430032）

0 引言

近年来，由于雷达和通信在硬件和软件上的相似性，其减少了许多电磁干扰问题，雷达与通信的一体化得到了越来越多的关注。但为了提高集成性能，有必要研究集成信号。然而，由于资源有限，它面临着一些挑战，包括波形、带宽、收发器等。许多研究者研究了这些资源的设计和适当分配。

参考文献[6]利用加权脉冲序列，将Oppermann序列元素作为复值权值，推导了具有Oppermann 序列的加权脉冲序列的模糊函数的解析表达式。给出了一组Oppermann 序列，证明了相关的模糊度函数只依赖于一个序列参数。参考文献[7]提出了一种用MSK 调制LFM 信号产生的兼容波形，主要探讨了其模糊函数(Ambiguity Function，AF)以及波形参数对AF 的影响。通过增加比特数可以获得较接近图钉形状的雷达波形。参考文献[8]提出了一种基于联合FRFT-ML 的2FSK-LFM 复合信号估计新方法。推导了复合信号在傅立叶变换域的表示，估计了复合信号的线性调频斜率和码长。结合ML 方法，提出了一种高精度的局部搜索方法，并对复合信号的载波频率进行了估计。结合ML 方法，提出了一种高精度的局部搜索方法，并对复合信号的载波频率进行了估计。参考文献[10-11]详细介绍了MFSK调制解调的具体原理和误码率分析。

本文提出了一种结合雷达步进频率信号和通信MFSK 调制的信号模型。先分别分析了MFSK 调制的通信性能和步进频雷达的模糊函数性能，然后将步进频信号与MFSK 通信调制相结合生成MFSK-步进频雷达通信一体化波形。本文以M=2 为例，分别从雷达模糊函数、模糊度函数、时域和频域步进脉冲序列的主峰4 个角度，分析了2FSK-步进频雷达通信一体化波形的雷达模糊函数性能。

1 MFSK-步进频雷达通信一体化波形设计原理

1.1 2FSK 信号基本原理

二进制频移键控信号符号的“1”和“0”分别以两个不同频率的正弦波形发送。因为它的幅度和初始相位保持不变，所以通信信号的传输不会受到相位随机抖动和幅度中随机抖动的干扰[8]。其表达式如式（1）所示[9]。

在式（1）中，假定符号的初始相位分别为φ1和φ0。ω1=2πf1和ω0=2πf0是具有不同频率的两个符号的角频率。A是常数，表示符号的包络是矩形脉冲。使用频率调制来生成2FSK 信号的方法如图1 所示。它使用二进制基带矩形脉冲信号调制频率调制器，然后输出两个不同频率的符号。频率调制器生成的2FSK 信号的相位在相邻符号之间是连续的。使用切换开关来生成2FSK 信号的方法如图2 所示。其原理是使用由基带脉冲控制的开关电路来选择两个独立频率源的振荡作为输出，因此相邻符号的相位不一定是连续的。

图1 2FSK 信号的产生方法——调频法

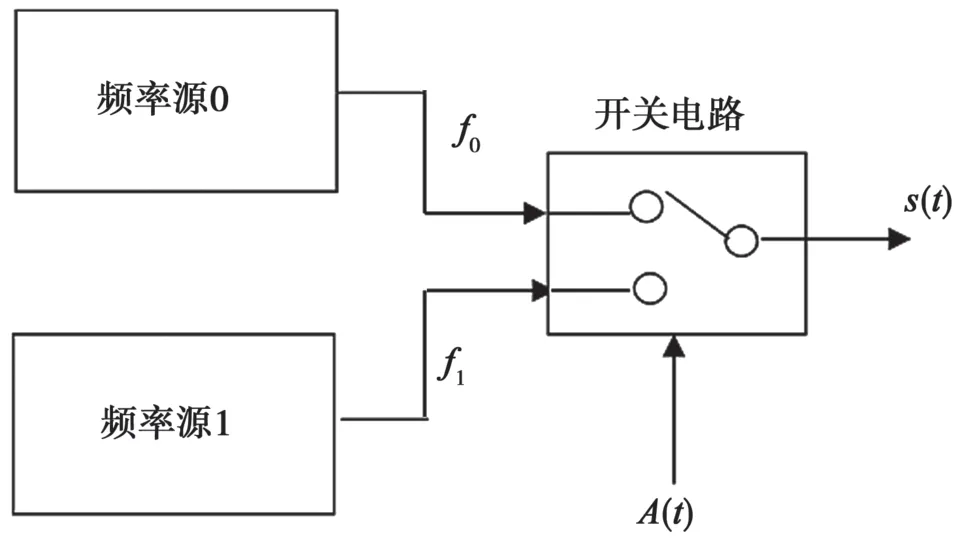
图2 2FSK 信号的产生方法-开关法

1.2 2FSK 功率谱密度——开关法

可以将通过切换方法生成的2FSK 信号的符号序列视为两个不同频率的2ASK 信号的叠加。因此，可以简单地从2ASK 信号的功率谱密度中得出功率谱密度[14]。

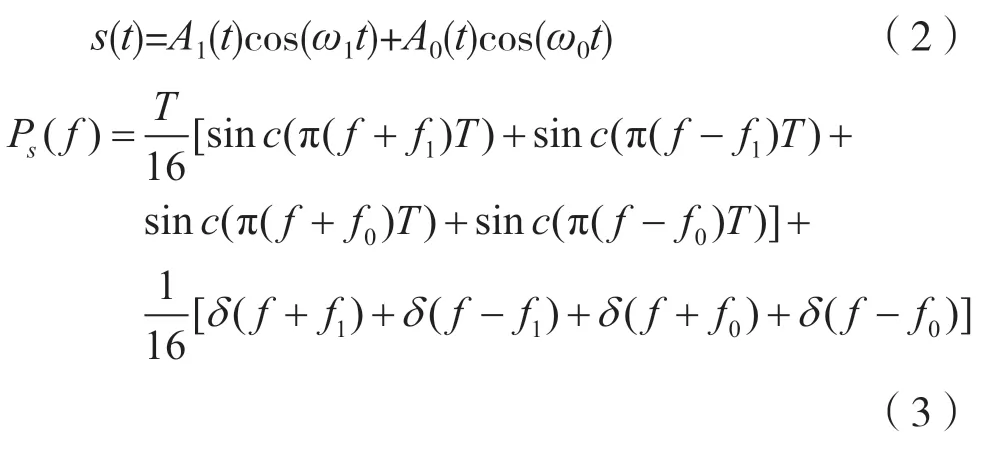
观察式（3），发现2FSK 信号的功率谱密度包含两个部分：连续谱和离散谱。前四项是连续频谱部分，后四项是离散频谱部分。2FSK 信号的功率谱密度曲线如图3 所示。观察图3，发现当2FSK信号的两个频率间隔比较小时，曲线只有一个峰值。较大时会出现双峰。当它大于2fc时，其双峰被完全隔离。2FSK 信号的带宽大约为Δf=|f1-f0|+2fc，这是在频谱的第一个零点内传输功率所需的带宽。fc是2FSK 信号频谱的中心频率，称为2FSK 信号的载波频率。

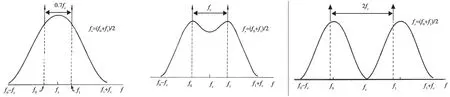
图3 FSK 信号的功率谱密度曲线（正频率部分）

1.3 2FSK 调制的最小频率间隔

如果f0和f1之间的间隔为2fc=2/T，显然它们可以被过滤器完全分开（实际上，滤波器的过滤效果很难实现严格的矩形窗口）。现在讨论最小允许频率间隔。原则上，如果两个信号彼此正交，则可以将它们完全分离。为了满足正交性条件，要求：

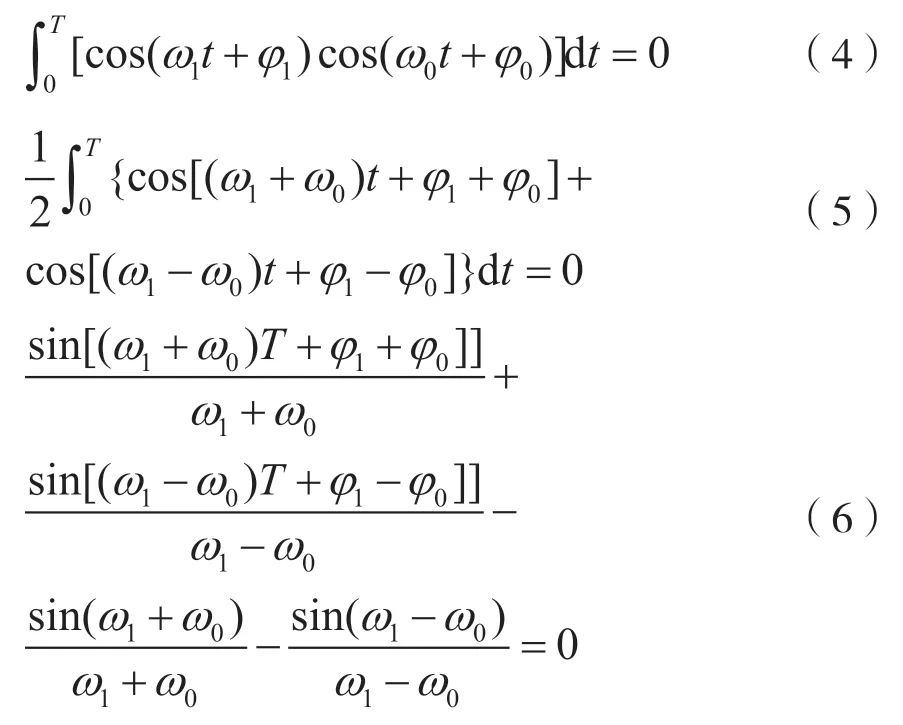
假设ω1+ω0=1。左端第1 项和第3 项近似等于0，因此其简化：

在满足条件的情况下，可得式（10）。当m=1时，可得最小频率间隔为1/T。

1.4 包络检波下2FSK 信号的误码率

2FSK 信号的接收分为两种：相干接收和非相干接收。在无线电信道中，由于诸如噪声之类的干扰，接收信号的相位不断地随机变化，这在实际中很难实现相干接收；相干解调方法需要生成具有相同频率和方向的局部载波，因此比包络检测要复杂得多。总之，2FSK 信号的接收大多采用包络检测方法[10]，其检测原理如图4 所示。

由于n(t)是窄带高斯过程，因此n(t)的表达式为[11]：

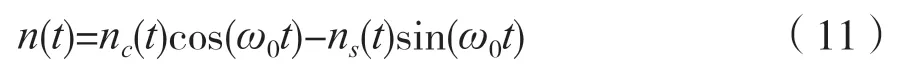
接收2FSK 信号的包络检测方法如图4 所示。包络线检测方法中，整流器的输出是经过低通滤波后的输入电压的包络线。发送符号“1”时，采样判决器的两个输入电压分别表示为：

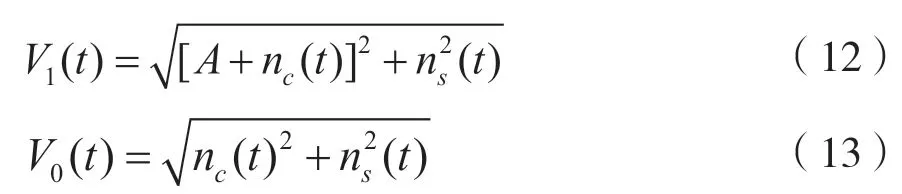
式中，V1(t)是对应频率为f1的码元通路的信号包络；V0(t)是对应频率为f0的码元通路的信号包络。

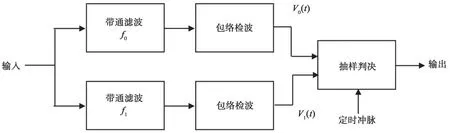
图4 2FSK 信号的包络检波原理图

V1(t)服从广义瑞利分布，V0(t)服从瑞利分布[12]。在抽样时刻，若V1(t)的抽样值V1小于V0(t)的抽样值V0，则判决器将发生错误判决。误码率为：

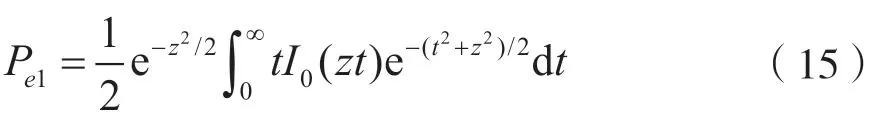
根据Q函数的性质，改写式（15）为：

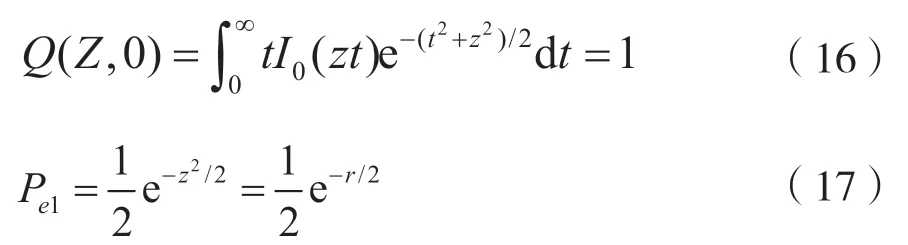
式中，r=z2=A2/2σn2为信噪比。

当发送符号“0”时，错误发生的情况完全相同，因此2FSK 包络检测期间的总误码率如式（18）所示。包络检波下2ASK 的误码率为[13]。比较2FSK和2ASK 的误码率，发现为了获得相同的误码率，2ASK 信号所需的功率比2FSK 信号的功率大3 dB。

1.5 多进制频移键控(MFSK)

多进制频移键控（Multibase Frequency-Shift Keying，MFSK）系统是2FSK 系统的简单扩展。在4FSK 中，使用4 个不同的频率表示四元符号，每个符号包含2 bit 信息，如图5 所示。此时，条件仍然与2FSK 中的条件相同，也就是说，每个载波频率之间的距离必须足够大，以使不同频率的符号频谱能够被滤波器分开，或者使不同的符号彼此正交。由于MFSK 的符号使用M个不同频率的载波，因此它占据了较宽的频带。如果f1是最低载波频率，而fm是最高载波频率，则MFSK 信号的带宽大约等于fM-f1+Δf。其中，Δf是单个符号的带宽，它取决于信号的传输速率。

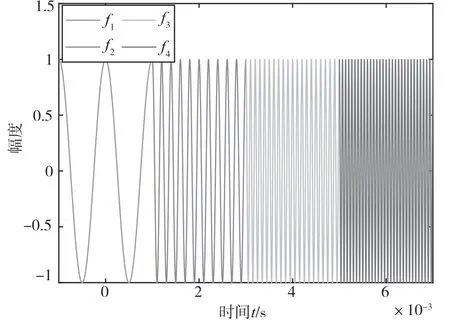
图5 4FSK 信号的调制原理

表1 4FSK 中频率与符号的对应关系

MFSK 信号非相干解调器的原理框图如图6 所示。这时，将有M个带通滤波器用于分离不同频率的M个符号。当输入某个符号时，M个带通滤波器的输出中只有一个是信号加噪声。在其他道路上只有噪声。现在假设M个通道带通滤波器中的噪声是相互独立的窄带正态分布噪声，并且其包络服从瑞利分布[16]，因此（M-1）个噪声的包络不超过确定的阈值水平h的概率为[1-P(h)]M-1，其中P(h)是滤波器的输出噪声包络超过该阈值h的概率。根据瑞利分布公式，可以得出式（19），其中N是滤波器输出噪声的包络，是滤波器输出噪声的功率[19]。

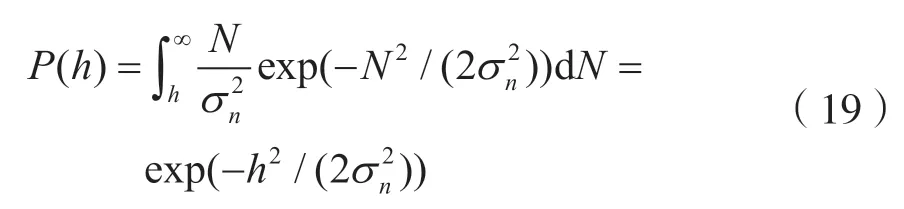
图6 MFSK 非相干解调原理方框图

假设（M-1）个噪声的输出噪声包络超过该阈值h，则不会发生错误的决定。因此，如果任何一个或多个噪声输出的包络超过该阈值，判决器将发生错误的判决。式（20）中显示了错误决策的可能性。显然，它与阈值h有关。

信号经过带通滤波器的输出电压是信号和噪声之和，因此其包络服从广义瑞利分布。在式（21）中，x是输出信号和噪声之和的包络。A是输出信号符号的幅度。是输出噪声功率。x是上限阈值h。换句话说，如果其他任何一条路径的输出电压值超过信号路径的输出电压值，那么将做出错误的判断。因此，式（22）中将显示错误决定的可能性。

将式（19）、式（20）和式（21）带入式（22），得出计算结果如式（23）所示[17]，其中是二项式展开系数。式（23）是一个正负交替的多项式。可以证明其第一项是其上界[18]，即式（24）。在式（24）中，A是信号幅度；是噪声功率；E是能量的象征；是噪声单边带功率谱密度；r是信噪比。由于r=krb，式（24）可用于获得式（25）。在式（25）中，用M代替（M-1）/2，右端的值将增加，但是这种不等式仍然成立，因为，所以可以得到式（26）：

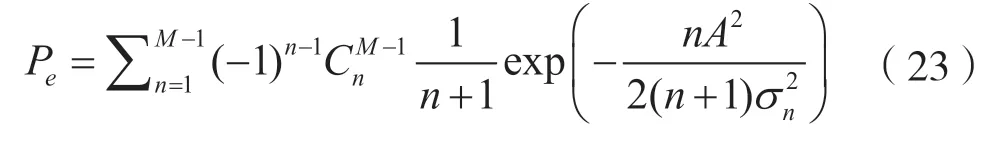
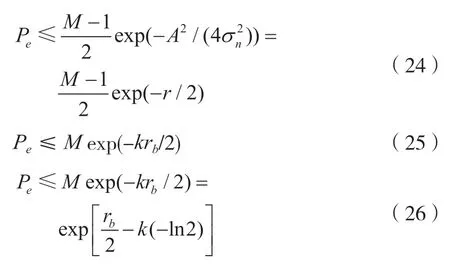
观察式（26），当k→∞时，Pe根据指数定律逼近0，但必须确保，即rb＞2ln2。

式（26）的条件要求信噪比rb＞1.39。在这种情况下，只要k足够大，就可以获得任意小的误码率。对于MFSK 系统，将占用更宽的带宽以换取降低误码率。但是，随着k的增加，设备的复杂性也成倍增加。因此，k的增加受到实际应用条件的限制。

上面计算的是误码率，即符号错误概率。现在来看符号错误率Pe和MFSK 信号的比特错误率Pb之间的关系。假设当M元符号中发生错误时，它将随机成为其他（M-1）个符号之一。由于M进制信号具有M个不同的代码元素，所以每个代码元素包含k个比特，即M=2k。因此，在任何给定的比特位置，出现“1”和“0”的符号的一半，即出现“1”的符号是M/2 种，出现“0”的符号是M/2 种。在2 表中，M=8，k=3，任何列中有4 个“1”和“0”。因此，如果一个符号与另一个符号有误，则在给定的位位置发生错误的概率仅为4/7。一般而言，在给定符号中，任何位位置的信息与其他2k-1-1 类型符号的相同位置的信息相同。同一位置的2k-1种代码元素的信息不同。因此，在式（27）中示出了位错误率Pb和符号错误率Pe之间的关系。

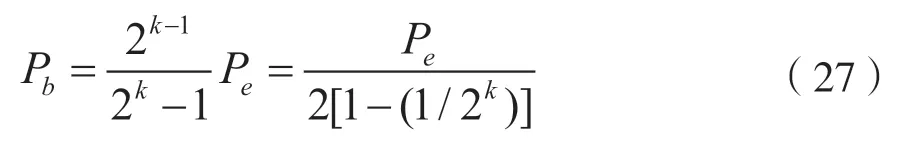
当k很大时，Pb≈Pe/2。

表2 M=8 时的码元

1.6 步进频率随机变化的MFSK-步进频信号

步进频率信号是雷达常用的大时间带宽乘积信号，可以在不增加系统瞬时带宽的情况下实现高范围分辨率。MFSK-步进频率信号的调制解调原理图如图7 所示。具有相等间隔的步进频率信号的特征在于，每个子脉冲具有固定的频率，相邻脉冲之间的频率间隔为固定的频率差Δf，其信号由式（28）确定[20,23]。

在式（25）中，fn=f0+(n-1)Δf是第n个子脉冲频率。在实现通信传输中，步进频率信号可以看作是特殊的MFSK 调制信号。步进频率信号的脉冲序列越多，MFSK 调制信号中的M值越大。当步进频率信号的脉冲序列的数量等于N时，步进频率信号的脉冲序列的数量只能取对应于2 的幂的数量。因为步进频率信号在同一时间发送M个频率脉冲，此时当使用按频率发送的不同通信符号时，无法知道哪个频率对应最先到达的通信符号，因此步进频率信号本身无法通过该频率。

在2FSK 信号中，基本频率为f0，f0=f-Δf，f1=f+Δf。当基本频率为0 时，2FSK 调制使用频率差±Δf表示通信信息。根据这一思路，针对步进频率信号，设计了基于步进频率信号的MFSK 雷达通信的积分波形，并采用频差法表示不同的通信信息。由于通信信号的随机变化，相邻信号之间的频率差是随机的。通过再增加一个脉冲序列来保持雷达带宽不变，因此，发射脉冲序列的总数为N+1（最后一个频率差不传达脉冲信息）。当M等于n1时，意味着步进频率信号的频率差是从n1个频率中随机选择的。不同的频率差对应于不同的通信符号。本文基于参考文献[21]，提出了一种改进的步进频率信号，如式（29）所示，其中k是任意正实数（可以是十进制）。

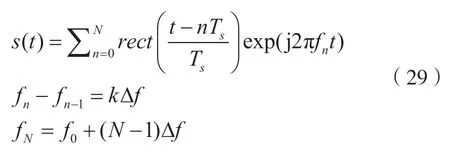
1.7 MFSK-步进频信号的调制解调原理

观察图7，解调时每个带通滤波器滤出得到一个频率的信号，FFT 变换后观察频谱得到fi，根据fn-fn-1的差值来判断通信输出符号。以2FSK 为例，fn-fn-1在f0和f1中随机取值。当fn-fn-1=f1时，传输通信符号“1”；当fn-fn-1=f0时，传输通信符号“0”。

图7 MFSK-步进频率信号的调制解调原理图

1.8 MFSK-步进频率信号的模糊函数

雷达模糊度函数的定义显示在式（30）中，其中u(t)是信号的复数包络[22]。频率步进信号将宽带信号离散化为N个频率点，N个脉冲形成一个帧，并且每个频率点都单独发送。本文为随机步骤，将步骤设置为Δf，第n个脉冲载波频率为fn，n个脉冲的组合带宽为nΔf，脉冲重复周期为Tr，每个调频子脉冲的宽度为τc，子脉冲带宽为B，频率步进发射信号的归一化表达式如式（31）所示。式（32）中显示了MFSK 步进频率信号的模糊函数。令p=m-n，记住fp=fm-fn，简化式（32）即可得到：

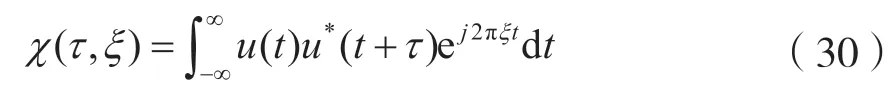
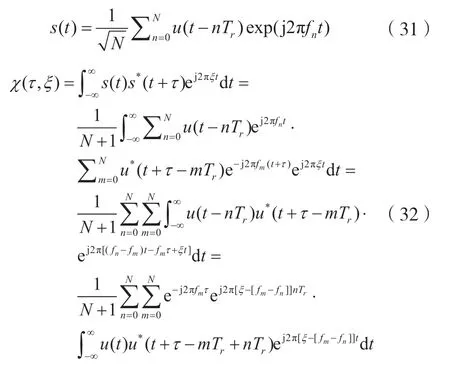
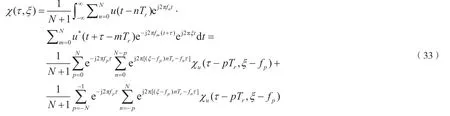
2 性能仿真

2.1 通信性能仿真

2FSK 的simulink 仿真原理图和仿真图如图8和图9 所示。2FSK 信号的调制原理图如图10 所示。观察图10 中的第2 张图，发现FSK 调制是通过不同的频率来传输不同的通信符号，其中符号“1”对应的频率大于符号“0”对应的频率。当把LFM信号当作FSK 调制对应的载波时，信号的频率会随时间不断发生变化，有可能出现符号“1”对应的频率大于符号“0”对应的频率，进而导致错误的判决，因此从这点上看FSK 调制不适合采用LFM信号作为载波。AWGN 信道中2FSK 调制对应的误码率曲线如图11 所示。观察图11 中的仿真曲线，好的仿真效果验证了仿真的准确性。

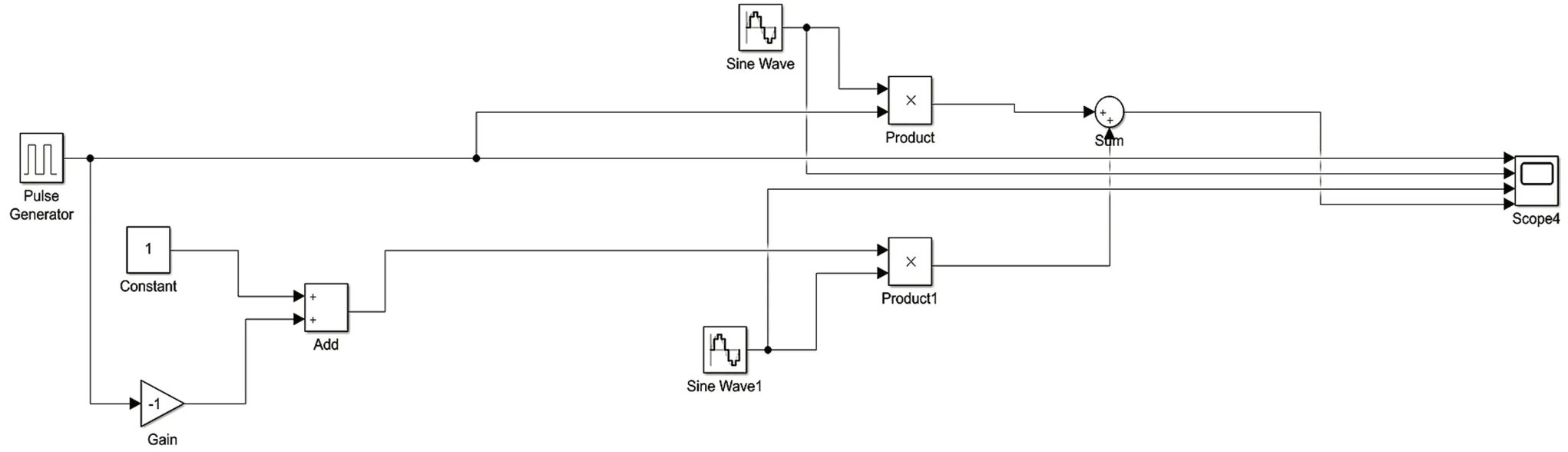
图8 2FSK 的simulink 仿真原理图

图9 2FSK 的simulink 仿真图

对应于式（27）的理论误码率曲线如图12 所示。图中的横坐标为rb，它是每位能量与噪声功率谱密度的比率。给定误码率，所需的rb随着M的增大而减小，即所需的信号功率随着M的增大而减小。但是，由于M的增大，MFSK 信号占用的带宽也增大了，这相当于将频带交换为功率。

基于随机频率差的MFSK-步进频信号的误码是由于频率差过近导致带通滤波器无法把其余频率杂波滤除掉而产生的。这个误码产生的原理与MFSK 调制下误码产生的原理是一样的，因此其误码率也是一样的。由于雷达发射脉冲是不连续的，受制于雷达本身的特性，当雷达发射脉冲间隔与脉冲持续时间一样时，基于随机频率差的MFSK-步进频雷达通信一体化信号发射的通信信息比单个MFSK 通信系统发射的通信信息少一半。

2.2 雷达性能仿真

根据步进频率脉冲序列信号模糊度函数的具体表达式，可以分析其模糊特性。为了直观地显示分析结果，采用无单元雷达系统参数进行计算机仿真。

仿真参数：脉冲宽度τ=1 μs，脉冲重复周期Tr=5μs，脉冲周期数N=4，频率步进增量Δf=1MHz，时间轴间隔Δτ=0.1μs，频率轴间隔Δfd=0.02MHz。

2.2.1 步进频雷达性能仿真

图13～图16 为步进频信号的雷达模糊函数。步进频率脉冲串信号的模糊图由互不重叠的模糊带组成。在整个时频表面的分布步进频率脉冲串信号采用了离散线性调频技术。从时频面投影图上可见到线性时间轴上脉冲宽度变窄，因此其距离分辨率得到提高。由于采用了脉冲串形式，步进频率信号的等效时宽增加到NT，提高了速度分辨率。

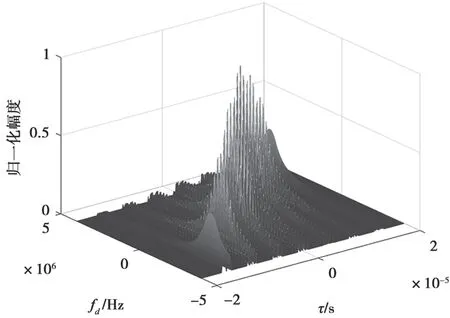
图13 步进频信号的模糊函数

图14 频率步进脉冲序列的模糊图

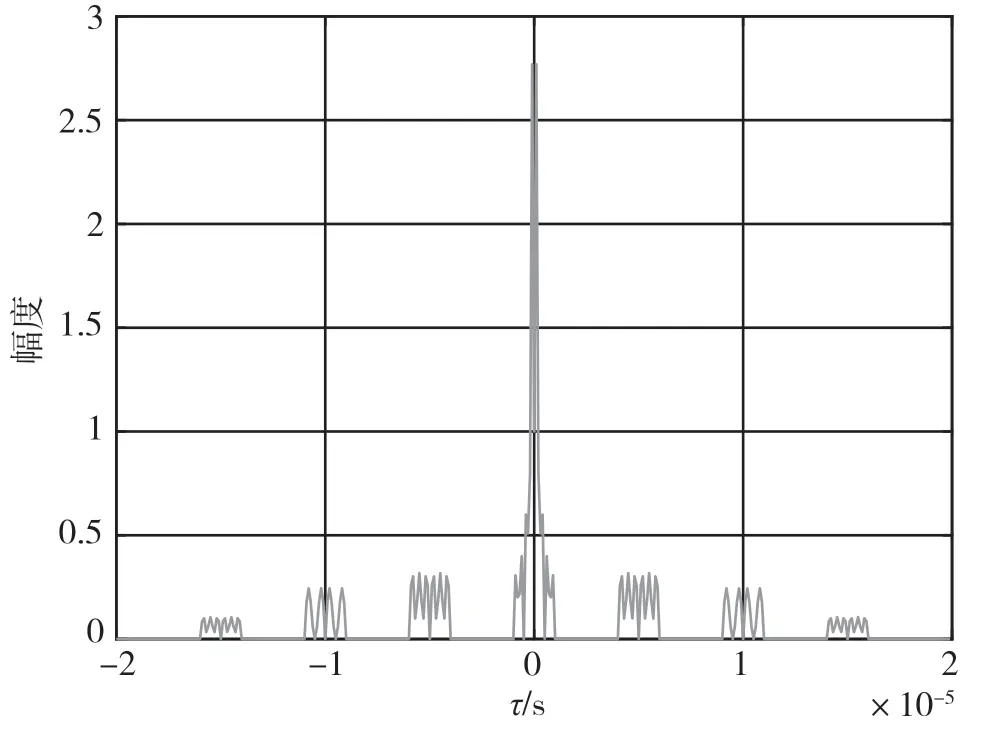
图15 频率步进脉冲序列时域中的主峰

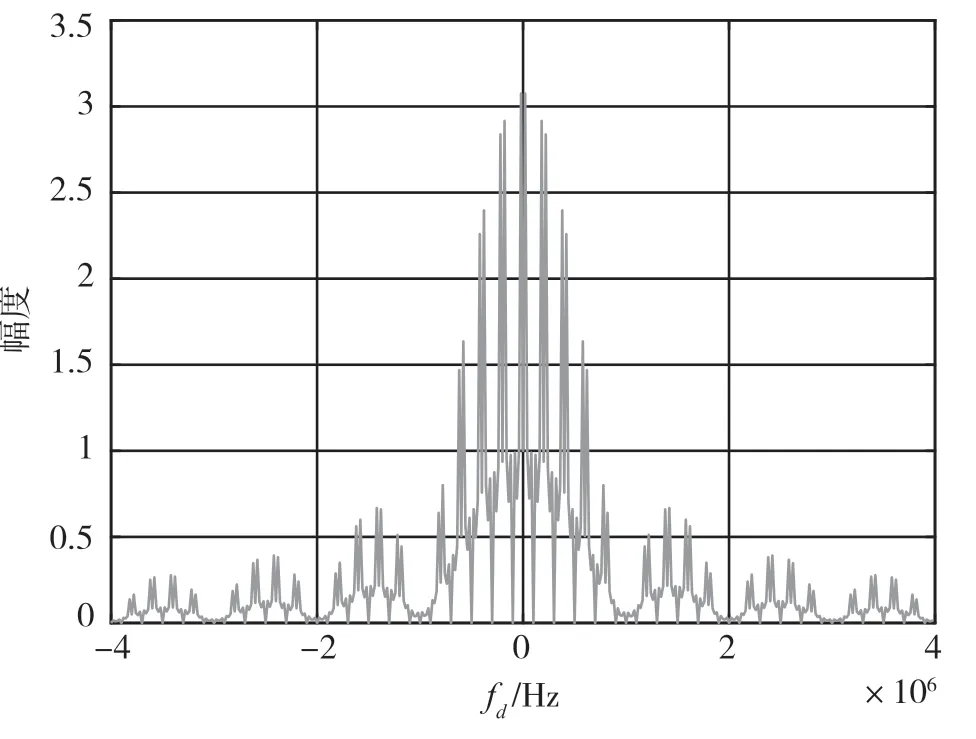
图16 频率步进脉冲串的频域主峰

与相同雷达参数的恒定载频脉冲串信号相比，在保持高速度分辨率的同时，步进频率脉冲串信号获得更高的距离分辨率特性，并且其距离模糊旁瓣衰减更快。步进脉冲串信号的这些特点加上小的瞬时带宽使它成为高距离分辨率信号形式之一。

2.2.2 基于随机频率差的2FSK-步进频雷达性能仿真

图17～图20 为基于随机频率差的步进频信号的雷达模糊函数。由于通信符号的随机变化，步进频率随机变化，因此模糊函数的幅度随机变化。对比图13 和图17，由于通信符号的随机性影响，时域频率步进脉冲序列的旁瓣变得更大。对比图16 和图20 发现通信符号的随机性不影响步进脉冲序列频域中的主峰和旁瓣。对比图15 和图19，发现随机的通信符号会使时域步进脉冲序列主峰旁的旁峰随机变大。

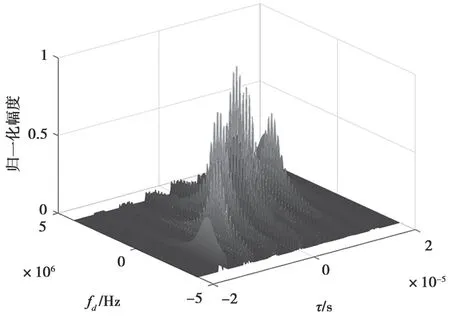
图17 随机频率差的频率步进脉冲序列的模糊函数

图18 具有随机频率差的步进脉冲序列的模糊

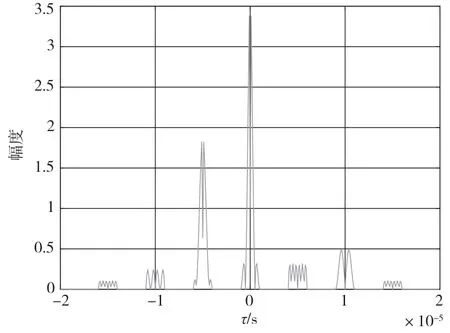
图19 时域随机频率差频率步进脉冲序列的主峰

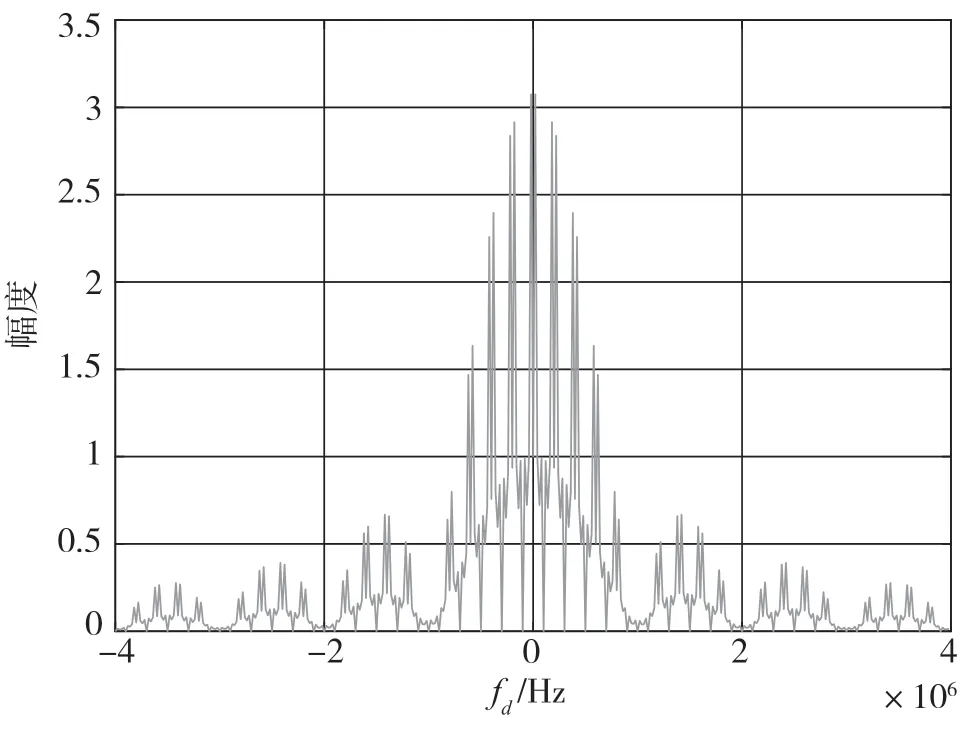
图20 具有随机频率差的步进脉冲序列频域中的主峰

3 结语

不可否认，一体化的雷达通信波形在性能上肯定劣于单个雷达和通信系统。在保证通信性能不变的条件下，本文设计步进频雷达-MFSK 雷达通信一体化波形可以有效地逼近雷达性能。

从调制雷达通信一体化信息的角度出发，本文提出了一种基于步进频率信号的一体化雷达通信波形。结合步进频率信号和频移键控调制方法，建立了步进频率-MFSK 一体化信号模型。通过推导雷达通信一体化信号模糊函数χ(τ,ξ)，可以很明确地知道随机通信信息的调制对一体化信号检测性能的影响。仿真实验结果表明该波形解决了时分或频分波形设计方法所造成的时宽和带宽浪费。随机的通信信息对频域步进脉冲序列无影响，但是其对时域的步进脉冲序列有负面的随机影响。