Controlling the entropic uncertainty and quantum discord in two two-level systems by an ancilla in dissipative environments∗

Rong-Yu Wu(伍容玉) and Mao-Fa Fang(方卯发)

Synergetic Innovation Center for Quantum Effects and Application,Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,Hunan Normal University,Changsha 410081,China

Keywords: entropic uncertainty,quantum discord,dissipative environment,ancilla

1. Introduction

On the other hand, quantum discord (QD) is a basic resource of quantum engineeri ng, defnied by Olliver and Zurek[13]and modified by Henderson and Vedral,[14]considering a more general measure of quantum correlations than entanglement,which also captures correlations that do not come into the domain of quantum entanglement and can be nonzero even for some separable states. Compared with entanglement,it has been shown that QD is more robust either in the Markovian environments[15]or in a non-Markovian environment[16]and can be created by local noise.[17,18]

In reality,a quantum object is susceptible to its surrounding environment, which will inevitably result in decoherence or a dissipative effect of the system concerned and the loss of information of systems and then leads to an increase in EU and a decrease in QD of systems. With this in mind,it is of fundamental importance to make it clear how diverse decoherence affects the dynamics of EU and QD under the open systems.Till now, in order to avoid or delay the influence of decoherence, some methods have been proposed to reduce EU and enhance QD. Nowadays, weak measurements[19]and quantum error correction[20]have been employed to reduce EU.In addition,it has been proven that quantum Zeno effect[21]and quantum coherence can protect QD.[22]Recently,Pati et al.[23]showed that QD can tighten the EUR in the presence of quantum memory. There are some researches that also studied in a general sense of the relations between EUR and QD.[24-26]In this paper, we investigate the EU of the observed system and the QD between the observed system and the quantum memory system in two two-level systems by an ancilla in dissipative environments.

This paper is organized as follows. In Section 2, we briefly review the definition of EUR and QD. In Section 3,we present the physical model of our system. In Section 4,the numerical results of EU and QD for the cases without and with the ancilla,and provide an effective strategy to further reduce EU and to protect QD by means of a Markovian feedback based on quantum-jump control. Finally, we end our paper with a brief conclusion in Section 5.

2. Brief review of EUR and QD

In terms of the EU game model between two players,Alice and Bob: Bob sends an atom A, initially entangled with the other atom B which is regarded as a quantum memory,to Alice. Then Alice measures Sxand Sy, and announces her measurement choice to Bob.[9]Mathematically, EUR can be expressed by the inequality

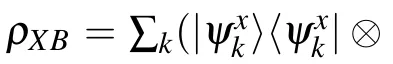
The total correlations between A and B can be displayed by quantum mutual information[29,30]

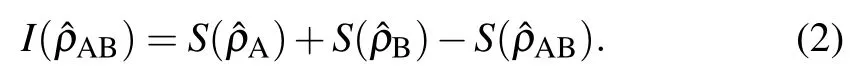
Based on this expression, it is believed that the correlations can be separated according to their classical and quantum natures.[31]The QD which quantifies the quantum correlation between A and B can be expressed as follows:

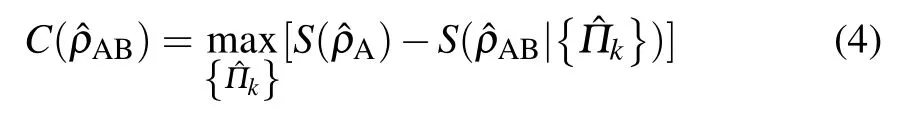
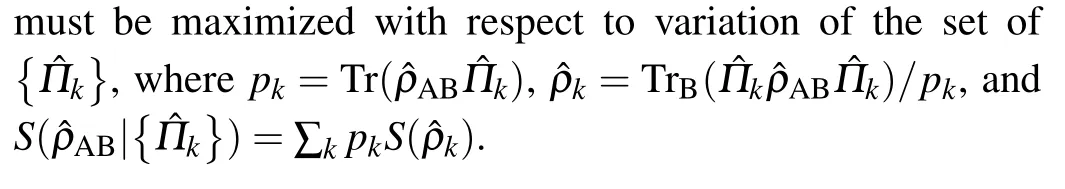
In this work, it is necessary to choose two orthogonal states. This must be constructed by such a way that the measurement projectors cover the complete Bloch sphere. We consider the bases |+〉 = cosθ|e〉+ eiφsinθ|g〉 and |−〉 =e−iφsinθ|e〉−cosθ|g〉, where the ranges for the angles are(0 ≤θ ≤π/2) and (0 ≤φ ≤2π).[34,35]Using the bases, we can evaluate the classical correlations.

3. The physical model

Our system is composed of three two-level systems, called qubits A, B and C, which are coupled symmetrically.[27,28]We assume that the two parts A and B are identical,they have the same eigenfrequencies ωA=ωB=ω,the interaction strength between A and B is J, the dissipative C acts as a ancilla whose eigenfrequency is ωC, the interaction strength JCbetween A and C is the same as B and C,the Hamiltonian of the whole system reads

The first two terms represent the free Hamiltonian of the three qubits, and the last two terms describe their interactions Hamiltonian. The inversion, raising and lowering operators associated with the qubit σz, σ+, σ−are defined as σz=|e〉〈e|−|g〉〈g|,σ+=|e〉〈g|and σ−=|g〉〈e|.

The state of this quantum system can be described by the density operator ρ which is obtained by tracing out the environment. The quantum master equation has been widely used to describe the dynamic behavior of open systems,and its purpose is to describe the time evolution of an open system with a non-unitary differential equation. We suppose that qubit A,qubit B and qubit C are coupled with the zero temperature heat reservoir respectively, the master equation describing the environmental decoherence under Markovian approximation is given by

Actually, in order to decrease the effect on decoherence of the given system mentioned above, Markovian quantum feedback control was first proposed by Wiseman[36]and Milburn.[37]It has been shown that the control can suppress decoherence in two two-level systems,[38]if we take quantumjump feedback control strategy into consideration. The master equation of Markovian is

where σ=(σx,σy,σz),A=(Ax,Ay,Az)represents the amplitude of σx, σyand σzcontrol. Once a quantum-jump event σ−ρσ+occurs,the unitary operator F is applied.

In order to explore the EU of the observed system A and the QD between observed system A and the quantum memory system B, we calculate the evolution of system density operator ρ and then trace out the third qubit to get the reduced matrix,

4. Results and discussion

4.1. The EU and QD without the ancilla

Before investigating the influence of the dissipative ancilla C,we first explore the case without the ancilla. At times t →∞, when system A and B are in their own independent environment,and coupled to each other,in the case of JC=0,we can calculate the steady-state density matrix analytically by solving L[ρ]=0 from Eq.(6)in the bases|11〉,|10〉,|01〉,|00〉,

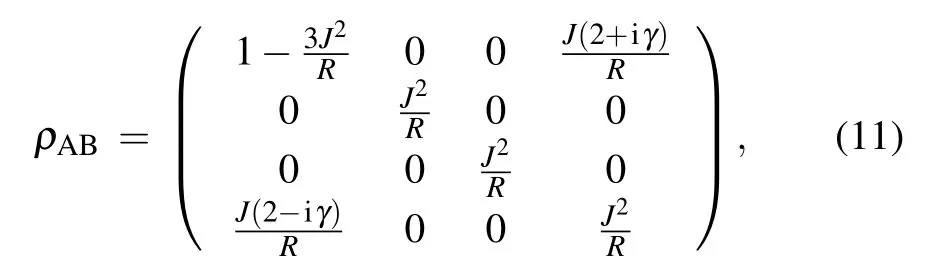
with R=4+4J2+γ2. It is worth noting that we measure all parameters in our system in units of ω, and pick γ =10−3.This seems reasonable at state of art experiments,[39,40]where eigenfrequencies of solid-state qubits are usually in the range of gigahertz,and at the same time decoherence parameters are estimated to be in the lower megahertz regime.

To better understand the EU and QD in the current model,we introduce the mixedness of a state,expressed as

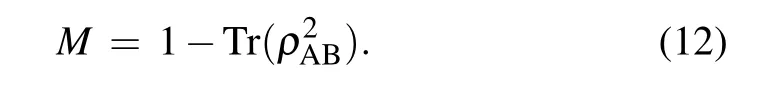
Substituting Eq.(11)into Eqs.(1)-(4)and(12),we can obtain the EU,QD and mixedness.

In Fig.1,the EU,QD and mixedness of the qubits in the steady state as a function of J are presented. It is clear that the sign of the coupling strength J is of no importance for the EU and QD in the case without the ancilla JC=0. Specially,under the dissipative environment,we observed that the higher the mixedness of the state ρABis,the larger the QD is. Thus,it is evident that the EU is positively correlated with the mixedness of ρAB. In this case,there is an increase in the mixedness of the system owing to the interaction between qubits A and B,which result in an increase in EU.

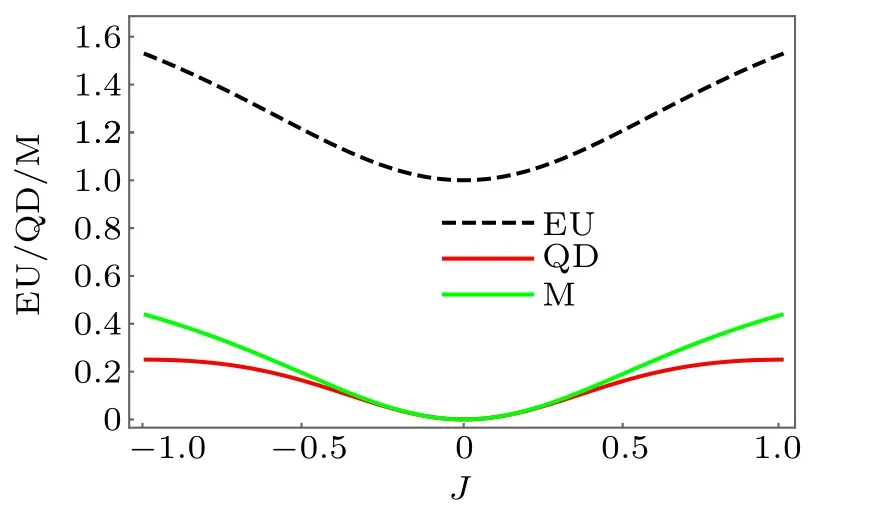
Fig.1. The EU,QD and mixedness of the qubits in the steady state as a function of J in the case without the ancilla. Here we set the parameter γ =10−3,the parameters in our system are in units of ω.

4.2. The EU and QD with the ancilla

Now we investigate if the ancilla C can reduce the EU and improve the QD in the strongly coupled region |J|=0.5 by choosing proper eigenfrequency and coupling strength of C.

By solving Eqs. (6) and (10), we can obtain the density matrix in the steady state for the two qubits A and B numerically. Under the condition of the steady state,the decrease of EU and the increase of QD caused by adding an ancilla C are shown in Fig.2. When J takes the positive value, the minimum value 1.207 for EU and a maximum value 0.160 for QD can be determined from the data file formed in Figs.2(a)and 2(c). In Figs. 2(b) and 2(d), it is shown that a minimum of EU is 1.151 and a maximum of QD is 0.171 by choosing the same parameters. In addition,from Fig.1 in the case without the ancilla, it is observed that the minimum value of the EU is 1.214,while the maximum value of QD is 0.163. These results indicate that,on the one hand,in the case with dissipative ancilla,a negative J is beneficial to the decrease of the EU and the increase of the QD;on the other hand,compared with the case without the ancilla, we can obtain lower EU and higher QD by adding the dissipative ancilla and letting J be negative.

Fig.2. The EU and QD as a function of JC and ωC in the case with the ancilla in the steady state,where we set the parameter γA=γB=γC=10−3 and|J|=0.5. The EU in(a)and(b),the QD in(c)and(d)for different signs of the coupling strength J. In(a)and(c),J=0.5;in(b)and(d),J=−0.5;the parameters in our system are in units of ω.

In principle,all parameters are adjustable,such as eigenfrequencies, coupling strengths and the decoherence parameters. From the above analysis we know that the EU can be reduced and QD can be enhanced by adding ancilla C for t →∞,but the change is small.Thus we try to make a higher degree of the change by choosing the right set of parameters. In order to study the dynamical process of system evolution, we assume that the three qubits are initially prepared in the state

There is a maximal entanglement when the state ρ(0) is reduced to the bipartite system of A and B. Substituting the initial state into Eq. (6), the time evolution of density matrix can be obtained numerically. In Fig.3, we fix the reasonable choice γ =10−3with regard to experiment and other optimal parameters J =−0.5, γC=0.031, ωC=−0.62, JC=0.01.The sign of eigenfrequency ωCreflects anti eigenenergy and it can be tuned by superconducting solid-state systems in experiments with artificial atoms.[42,43]It can be seen from the figure that when the eigenfrequency of the ancilla system is negative, we can obtain lower EU and higher QD compared with the case of positive value. Obviously,this decrease of energy dissipation in the system is beneficial to the decrease in EU and increase in QD.Our results also show that there are a minimum value 0.737 for EU and a maximum value 0.725 for QD at γC=0.031,which are quiet improvements for EU and QD due to the existence of the dissipation ancilla. It is very intriguing from the fact that decoherence assists the EU to be decreased and the QD to be increased in this case,which is a counterintuitive result.

Fig.3. (a) EU and (b) QD versus ωC and γC in the case with the ancilla in the steady state,where we set the parameters γA=γB=10−3,J=−0.5 and JC=0.01,the parameters in our system are in units of ω.

Compared Fig.4(a) with Fig.4(b), it is easily to found that the EU can be decreased largely for t →∞. Meanwhile,the QD can be increased,the reason is that the subsystem B has the function of quantum memory in this case, so an increase in QD can lead to a decrease in EU.Thus,the energy dissipation in one subsystem can reduce EU of the observed system and enhance QD between the observed system and the quantum memory system. In order to explain this phenomenon,we draw lessons from the methods[41]to use the definition of state fidelity,

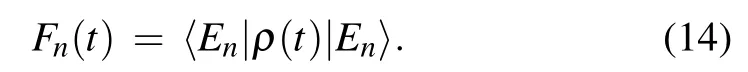
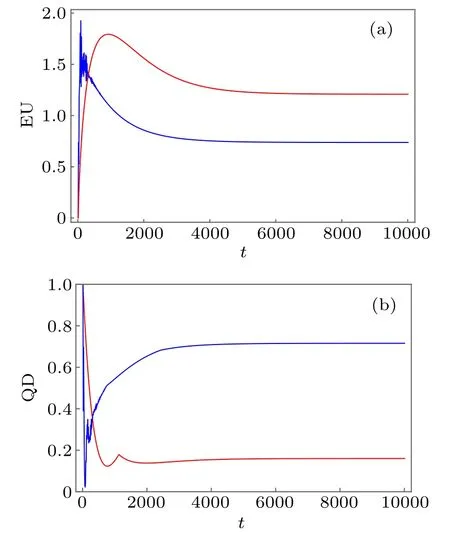
Fig.4. (a)Evolutions of EU in the case with the ancilla for JC/=0(blue solid curve)and without the ancilla for JC=0(red solid curve)for the initial state of Eq. (13) with the parameters γC =0.031, ωC =−0.62,JC=0.01,J=−0.5 and γ =10−3. (b)Evolutions of quantum discord in the case with the ancilla for JC/=0(blue solid curve)and without the ancilla for JC =0(red solid curve)with the same parameters as in(a).Here t is in units of 1/ω,the other parameters in our system are in units of ω.

Fig.5. Evolution of fidelities Fn(t) for the initial state of Eq. (13)with the parameters γC =0.031, ωC =−0.62, JC =0.01, J =−0.5 and γ =10−3. The eigenstate|E7〉has the highest fidelity,t is in units of 1/ω,and the other parameters in our system are in units of ω.

We can display the fidelities of all eigenstates of the system in Fig.5 by choosing γC=0.031,ωC=−0.62,JC=0.01,J=−0.5 and γ=10−3as the same as the parameters selected in Fig.4. It is obvious that from the figure,the eigenstate|E7〉has the highest fidelity under the condition with this set of parameters,which demonstrates that the parameters in Fig.4 can prepare the state of the system to the highest excited state with hight fidelity.The eigenstate|E7〉possesses EU value 0.007 in subsystem A and QD value 0.999 in subsystem AB. Compared to the minimal possible bipartite EU of 0 and the maximal possible bipartite QD of 1 for a Bell state,one can understand why the EU is reduced and QD is enhanced to such a level in Fig.4 in this set of parameters.

4.3. The EU and QD based on the quantum-jump-based feedback control

In this section, we investigate the effect of the quantumjump-based feedback control on the EU and QD.We can obtain the atomic density matrix at time t numerically by substituting the initial state Eq.(13)into Eq.(7). In order to directly show the time evolution of the EU under quantum-jump-based feedback control,we plot the EU graph as a function of time t and the feedback parameter Ayin Fig.6. We can see that the EU is smallest during the evolution when the feedback parameter is 2π/5.

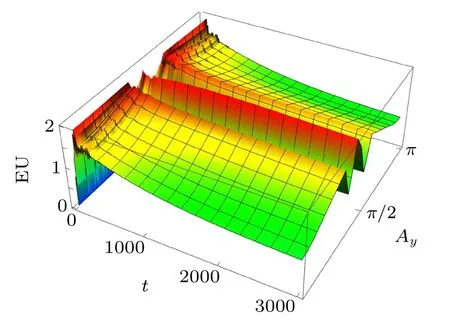
Fig.6. The time evolution of EU of the observed system Ay with different control parameters. The other parameters γC=0.031,J=−0.5,ωC=−0.62,JC=0.01,γ=10−3 are kept to be unchanged,t is in units of 1/ω,and the other parameters in units of ω.

Fig.7. (a) The time evolution of EU of the observed system A under the feedback control for Ay=2π/5(red solid curve)versus the uncontrolled case for Ay=0(blue solid curve). (b)The time evolution of QD under the feedback control for Ay =2π/5 (red solid curve) versus the uncontrolled case for Ay =0 (blue solid curve). Here t is in units of 1/ω,and the other parameters in our system is in units of ω.

In order to explicitly reveal this phenomenon, the time evolution of EU and QD for the two cases with feedback control Ay=2π/5(red solid curve)and without feedback control Ay=0 (blue solid curve) are plotted in Figs. 7(a) and 7(b),respectively. From the figure we can see that the EU can be reduced(shown in Fig.7(a))and QD can be increased(shown in Fig.7(b)) distinctly under quantum-jump-based feedback control. Therefore, the EU in the system can be restrained and maintain a low level for a long time by adjusting the feedback parameters, which show a good noise reduction effect.Meanwhile,the QD can also be relatively enhanced due to the quantum-jump-based feedback control.

5. Conclusion

In summary, we have studied the control of the entropic uncertainty and quantum discord in two two-level systems by an ancilla in dissipative environment. Our results show that the EU of an observed system can be reduced and the QD between the observed system and the quantum memory system can be enhanced in the steady state of the system by adding an dissipative ancilla under the condition with proper parameters of the system. We can conclude the following: First,by discussing two cases without and with dissipative ancilla,we have shown that the introduction of dissipative ancilla is conducive to the decrease of EU and the increase of QD in the steady state of the system. In particular,via preparing the state of the system to the highest excited state with hight fidelity, taking the eigenfrequency of the ancilla as negative,and choosing appropriate parameters of the system, EU can be reduced markedly and QD can be enhanced obviously. We have explained these results using the definition of state fidelity. Second, we present an effective strategy to further reduce the EU and enhance the QD via quantum-jump-based feedback control. Therefore, we claim that our explorations offer a method which can greatly reduce the quantum noise and enhance quantum correlation in the system,and may be of importance in the context of quantum information technologies.