Influence of sub-bandgap illumination on space charge distribution in CdZnTe detector∗

Rongrong Guo(郭榕榕), Jinhai Lin(林金海), Lili Liu(刘莉莉), Shiwei Li(李世韦),Chen Wang(王尘), Feibin Xiong(熊飞兵), and Haijun Lin(林海军)

Fujian Provincial Key Laboratory of Optoelectronic Technology and Devices,Xiamen University of Technology,Xiamen 361024,China

Keywords: CdZnTe detector,sub-bandgap illumination,space charge,charge collection efficiency

1. Introduction

Cadmium zinc telluride (CdZnTe) emerges as the leading semiconductor crystals for fabricating room-temperature x-ray and gamma-ray detectors,which were widely used in nuclear medical images,non-destructive inspection,scientific xray and gamma-ray imaging and spectroscopy.[1-3]However,various structural defects were inevitably induced into crystals during the complex crystal growth process,which is harmful to the carrier transport process and collection seriously via carrier trapping and recombination effect.[4]Especially when the detector worked in the high counting rate mode, the accumulation of the space charge at defect levels will cause electric field distortion and thus seriously deteriorate device performance.[5-8]Therefore,it is of great importance to understand the space charge accumulation mechanisms in the cadmium zinc telluride crystals and establish a method to avoid device damage caused by the space charge accumulation effect.

In recent years, many efforts have been made to study the effect of the sub-bandgap illumination on the device performance. Alekseeva et al.[9]showed that the sub-bandgap illumination could regulate the occupation state of electrons and holes in the deep level,thus improving the collection efficiency of devices. Washington et al. also found that the subbandgap illumination has a significant influence on the internal electric field distribution.[10]It has been demonstrated that the sub-bandgap illumination is effective for improving the charge collection efficiency under proper illumination wavelength and power. However, the changes of deep levels occupation, space charge distribution, and their relation with the electric field distribution under the sub-bandgap illumination have not been fully established in CdZnTe detectors.Meanwhile,how to select appropriate illumination conditions to suppress the adverse effects of the space charge accumulation in crystals is a considerable interest to focus on. The Silvaco TCAD simulation technique has high simulation accuracy, which has outstanding advantages in semiconductor device performance simulations.[11-14]So in the present research, the Silvaco TCAD simulation technique is applied to simulate the space charge distribution in CdZnTe crystal before and after sub-bandgap illuminations. The influences of the sub-bandgap illumination on the defect level occupation fraction, space charge, and internal electric field distributions are investigated systematically. At the same time, the influence of sub-band gap illumination on the charge collection efficiency of detector is also discussed. The simulation results will provide some theoretical guidance for improving the collection efficiency of CdZnTe imaging devices.

2. Silvaco TCAD simulation method description and model establishment

In this paper, Silvaco TCAD[15]is used to conduct (2D)numerical simulation of Au/CdZnTe/Au detectors to study the effect of the sub-bandgap illumination on the defect level occupation fraction,space charge,and internal electric field distribution in crystal. Three fundamental semiconductor equations: Poisson equation, carrier continuity equation, and current density equation are used in this paper. SRH recombination model, Auger recombination model, and optical generation/radiative recombination are applied to simulate the carrier transport processes, considering the recombination, trapping,and de-trapping effects in the simulation.

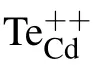
Fig.1. (a)Au/CdZnTe/Au device structure diagram,(b)defect energy level distribution in the CdZnTe crystal.

Table 1. Basic information about CdZnTe crystals.[17,20-22]

Table 2. Basic information about CdZnTe crystals.[17]

Table 3. Basic parameters of illumination conditions.[5,18,19,23]

3. Influence of sub-bandgap illumination on carrier concentration of CdZnTe crystals

To explore the influence of sub-bandgap illumination on the energy level occupation probability, the crystal is illuminated by a sub-bandgap illumination with wavelength of 890 nm and intensity of 8×10−8W/cm2. The simulation results of carrier concentration distributions in crystals before and after illumination are shown in Fig.2.

Fig.2. Carriers concentration(conc.) distribution of crystal(a)in dark, (b)under illumination.

The carrier concentration after illumination is much higher than before. At the same time,the bulk resistivities of CdZnTe in the dark and with sub-bandgap illumination are determined to be 6.66×109Ω·cm and 1.37×108Ω·cm, respectively. On thermal equilibrium, Femi level is near the middle of the energy band gap in CdZnTe crystals to achieve high resistivity. However, when CdZnTe crystal was illuminated,the quasi-Fermi energy level of electrons moved up,while that of holes moved down,[24]thus the concentration of carriers in the crystal is increased. As shown in Fig.2(b), the hole concentration increased largely in comparison with electron concentration after sub-bandgap illumination. The changes of carrier concentration and resistivity indicate that the probability of defect level occupation in the crystal is changed. The possible mechanisms of the carrier concentration changes will be discussed in the next section.

4. The influence of sub-bandgap illumination on ionized concentration of deep level and space charge distribution in crystals

Fig.3. Distribution of ionized deep donor level concentration (cons.) under different biases (a) 0 V, (b) 150 V, (c) 300 V before and after sub-bandgap illumination, (d) schematic diagram of MSM structure energy band under biases, (e) diagram of major processes containing a deep donor defect level in CdZnTe crystals under sub-bandgap illumination(arrow direction is the direction of electron transitions).

5. Influence of sub-bandgap illumination on internal electric field distribution and charge collection efficiency

Figure 4 shows the space charge distribution and internal electric field distribution under bias voltages of 150 V and 500 V before and after sub-bandgap illumination,respectively. The variation of space charge concentration under subbandgap illumination directly affects the electric field distribution in the CdZnTe crystal. The electric field distribution in the CdZnTe crystal can be calculated by Poisson equation[15]

The charge collection efficiency is the ratio of the quantity of carriers received by electrodes to the total quantity of carriers generated by implying the ray into the device. To further understand the effect of electric field on charge collection efficiency with sub-bandgap illumination. The famous Hecht equation[26]is utilized to analyze the collection efficiency(CCE)of the CdZnTe detector carriers,

where µeand τeare the mobility and lifetime of electrons,respectively, and the product of which is 3×10−3cm2·V−1,µhand τhare the mobility and lifetime of the hole, respectively,and the product of which is 5×10−5cm2·V−1.[26]E is the internal electric field,which is imported by Silvaco TCAD simulation. D is the thickness of the detector which is 0.1 cm in this simulation,and Z is the position where the incident ray interacts with the crystal.

Fig.4. (a)Space charge distribution in CdZnTe crystal under bias of 150 V,(b)under bias of 500 V,(c)internal electric field distribution of CdZnTe crystal under bias of 150 V,(d)bias of 500 V before and after sub-bandgap illuminations.

Fig.5. CCE distribution before and after sub-bandgap illuminations: (a)total charge collection efficiency and(b)charge collection efficiency of electron and hole.

The charge collection efficiency (CCE) of electrons and holes of the CdZnTe detector is calculated by Hecht equation,as shown in Fig.5.

As shown in Fig.5(a),the charge collection efficiency of the detector is significantly improved under the sub-bandgap illumination, especially in the area near the anode. Meanwhile,the charge collection efficiency of holes improved more significantly than electrons, as shown in Fig.5(b). This is mainly due to the sub-bandgap illumination,the internal electric field becomes flatten, which improves the total charge collection efficiency of the device. However, the charge collection efficiency of detector has already reached 97% at the distance of 0.01 cm from cathode without sub-band gap illumination. Thus, the improvement of detector collection efficiency under sub-bandgap illumination near the cathode is non-significant.

6. The influence of sub-bandgap illumination with different conditions on space charge distribution and charge collection efficiency

The simulation results of the resistivity of CdZnTe crystal under different sub-bandgap illuminations are shown in Table 4. It can be seen that with the increase of illumination intensity,the resistivity decreases gradually. When the illumination intensity is 5×10−7W/cm2,the resistivity is as low as the value of 2.89×107Ω·cm.In this section,on the premise of ensuring high resistance of crystals,three different wavelengths of sub-bandgap illumination (number 1-3) and six different illumination intensities of sub-bandgap illumination (number 3-7)are selected to explore their influence on ionized concentration,space charge,and internal electric field distribution of CdZnTe crystals.

Table 4. Resistivity of CdZnTe crystal under different sub-bandgap illuminations.

6.1. Effects of sub-bandgap illumination with different wavelengths on space charge distribution and charge collection efficiency

In order to further understand the influence of subbandgap illumination on the ionized concentration, space charge, and internal electric field distribution in crystals. In this section,the wafer is irradiated under three different wavelengths of 850 nm,890 nm,and 940 nm,respectively,with the illumination intensity of 8×10−8W/cm2.The relevant ionized concentration,space charge,internal electric field distribution,and charge collection efficiency obtained at bias voltage of 500 V are shown in Fig.6. It can be seen that, the ionized concentration of deep donor level under 850-nm illumination is significantly lower than that under 890-nm and 940-nm illuminations. And the space charge concentration under 850-nm illumination is lower,either,which results in a flatter internal electric field and more effectively improving charge collection efficiency of the detector. The simulation results correspond to the experimental results of Cola.[5]

Fig.6. (a)Distribution of ionized deep donor level concentration(conc.),(b)space charge concentration,(c)internal electric field,(d)charge collection efficiency under different subbandgap wavelengths and 500 V bias.

6.2. Effects of sub-bandgap illumination with different illumination intensities on space charge distribution and charge collection efficiency

The influences of different wavelengths on space charge distribution and charge collection efficiency have been investigated in the previous section. The simulation shows that the charge collection efficiency can be improved more effectively under the sub-bandgap illumination of 850 nm. Based on Table 4, the resistivity of the crystal decreases with increasing illumination intensity. When the illumination intensity is 5×10−7W/cm2at wavelength of 850 nm, the resistivity of crystal reaches as low as 107Ω·cm. To avoid introducing excessive leakage current due to illumination, different illumination intensities(3×10−9W/cm2,1×10−8W/cm2,8×10−8W/cm2, 4×10−8W/cm2, 8×10−8W/cm2, and 1×10−7W/cm2) under the bias voltage of 500 V and the wavelength of 850 nm are selected to simulate the ionized deep donor concentration distribution, space charge, internal electric field,and charge collection efficiency in crystals. The corresponding results are shown in Fig.7. As shown in Fig.7,different illumination intensities have different effects on the occupation probability of defect level in crystals. When the illumination intensity is 3×10−9W/cm2, the ionized deep donor level concentration(at the same position of the crystal)is significantly higher than that under other conditions. The larger ionization concentration of deep donor level, leads to an increase of space charge concentration in the crystal,which makes the internal electric field even more uneven. Therefore,it is detrimental to the charge collection of detectors. With the increase of illumination intensity,the concentration of ionized deep donor level decreases. When the illumination intensity increased to 1×10−7W/cm2,the concentration of the ionized deep donor level at the same position in the crystal is greatly reduced, thus reducing the concentration of space charge and making the internal electric field flattening. As shown in Fig.7(d), when the illumination intensity is 1×10−7W/cm2,the carrier collection efficiency at the anode position of the detector is significantly improved therefore, it is more effective in improving the overall charge collection of detectors.

Fig.7. (a) The distribution of ionized deep donor level concentration, (b) space charge concentration, (c) internal electric field, (d) carrier collection efficiency in the crystal under bias of 500 V,wavelength of 850 nm with different illumination intensities.

7. Conclusions

In this paper, the effects of sub-bandgap illumination on the space charge distribution, internal electric field distribution, and charge collection efficiency of CdZnTe detector are simulated using the semiconductor device simulation software named Silvaco TCAD.The simulation results show that,under sub-bandgap illumination with wavelength of 890 nm and light intensity of 8×10−8W/cm2, the sub-bandgap illumination promotes optical excitation of electrons from the valence band into the ionized deep donor levels (located in EV+0.86 eV with concentration of 1×1012cm−3). A neutral state of deep donor level is formed due to the increasing probability of deep donor levels being occupied by electrons. Thus, the space charge concentration is reduced in the crystal and the internal electric field turns to flat under the sub-band gap illumination.Therefore, the charge collection efficiency of the detector is significantly improved. When the wavelength of sub-bandgap illumination is 850 nm,the concentration of the ionized deep donor level and space charge at the same position of the crystal can be further reduced, thus making the internal electric field flatter. At this time,ensuring the CdZnTe crystal with high resistivity, enhancing the light intensity to 1×10−7W/cm2can also reduce the concentration of the ionized deep donor level and space charge.This results in a flatter internal electric field,which greatly reduces the probability of carriers being trapped or recombined by defect levels during charge transport processes and then significantly improves the charge collection efficiency of detectors.

Acknowledgment

The authors would like to give special thanks to Dr.Tao Wang from Northwestern Polytechnical University for the fruitful discussion during the writing of this paper.