Controlling multiple optomechanically induced transparency in the distant cavity-optomechanical system∗

Rui-Jie Xiao(肖瑞杰), Gui-Xia Pan(潘桂侠), and Xiao-Ming Xiu(修晓明)

1College of Physical Science and Technology,Bohai University,Jinzhou 121013,China

2School of Science,Anhui University of Science and Technology,Huainan 232001,China

Keywords: optomechanical system,optomechanically induced transparency,optical mode

1. Introduction

Cavity optomechanics,[1-7]which combines the mechanical and optical degrees of freedom via radiation pressure force, has recently arisen as a rapidly developing field. Many fascinating phenomena, such as optomechanically induced transparency,[8,9]signal amplification,[10]slow and fast light,[11,12]optical bistability,[13]and weak force measurement,[14,15]have been investigated in various cavity optomechanical systems. A wealth of possible applications for such devices in phonon lasers,[16]photon blockade,[17,18]and gravitational wave detectors[19]have also been proposed.

Optomechanical induced transparency(OMIT)as a novel optical phenomenon is analogous to electromagnetically induced transparency,[20]which plays an important role in quantum memories and repeaters.[1]In the presence of the pump field, a transparency window occurs in the probe transmission spectrum, which derives from the quantum interference effect. OMIT has been explored theoretically[21]and observed experimentally.[9,11,22]It can be employed for slowing and stopping light,[23]signal amplifications,[24]charge measurement,[25]and single-photon routers.[26]

Recently, double-OMIT and even multiple-OMIT have been studied extensively.[27-34]For example, double-OMIT has been carried out in the charged-resonators optomechanical system,[24,27]two mechanical resonators optomechanical system,[28]coupled-disks structure,[30]and two-cavity optomechanical system.[31]Meanwhile, the multiple-OMIT has been achieved in N-resonators optomechanical system,[32,33]the atomic-media assisted single optomechanical system,[34]and two-cavity double resonators optomechanical system.[35]Double-and multiple-OMIT also have new applications,such as the all-optical quantum network and multi-channel quantum information processing.[36]

In addition,the mutual coupling between two mechanical resonators in hybrid optomechanical systems has also attracted widespread interest both in theory and experiment.[24,27,37-42]The two mechanical resonators can be coupled to each other via Coulomb interaction or the common coupling overhang.More importantly, the coupling strength can be modulated flexibly.[41,42]Based on these reasons,the natural question is:can we control the effect of OMIT by modulating the mutual coupling between the mechanical resonators?

In this work,we theoretically investigate a two-cavity optomechanical system in which the two cavities couple to each other via a distant waveguide, which is similar to Ref. [43].Each cavity couples to a mechanical resonator via radiation pressure force, and each mechanical resonator couples to an auxiliary mechanical resonator. Our study shows that the output probe field of the compound optomechanical system may have five transparent windows. It is worth mention that our scheme is essentially different from the previous studies,[32,33]where a multiple-EIT is caused by the mechanical arrays with different frequencies and different positions of the oscillators in the cavity. Our study is also different from the previous proposals,[44,45]where a multiple-EIT is caused by optical arrays and atom media. Furthermore, we find that the properties of the multiple-OMIT can be effectively tuned by several system parameters, including the classical driving power and the coupling strength between the two mechanical modes. Simultaneously, we find that the two furthest windows of the multiple-OMIT are apart near linearly with respect to the classical driving power Pland the coupling strength λ. Our scheme provides a method to control multiple electromagnetically induced transparency.

2. Model and analytical solution

Fig.1. Schematic diagram of the compound optomechanical system. It consists of two cavities and four mechanical resonators. The two cavities couple to each other with the interactive coupling strength J, and the two mechanical oscillators couple to each other with the coupling strength λ. The system is driven by a strong pump field and a weak probe field.

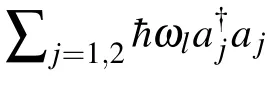
where

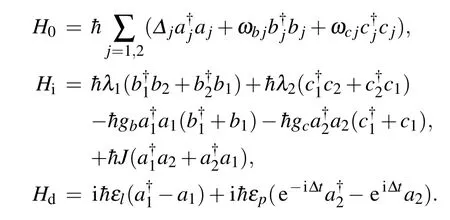
Introducing the corresponding dissipation and fluctuation terms, the quantum Heisenberg-Langevin equations can be written as

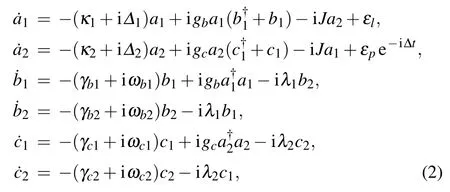
where κj, γbjand γcj(j = 1,2) are the decay rates of the two optical modes and the four mechanical modes, respectively. In the case of εl≫εp,we express the dynamical variables as the sum of their steady-state mean values and small fluctuations,[1]i.e.,Θj=Θjs+δΘj(j=1,2),where Θ represents the operators a,b,and c. The steady-state values of the dynamical variables are

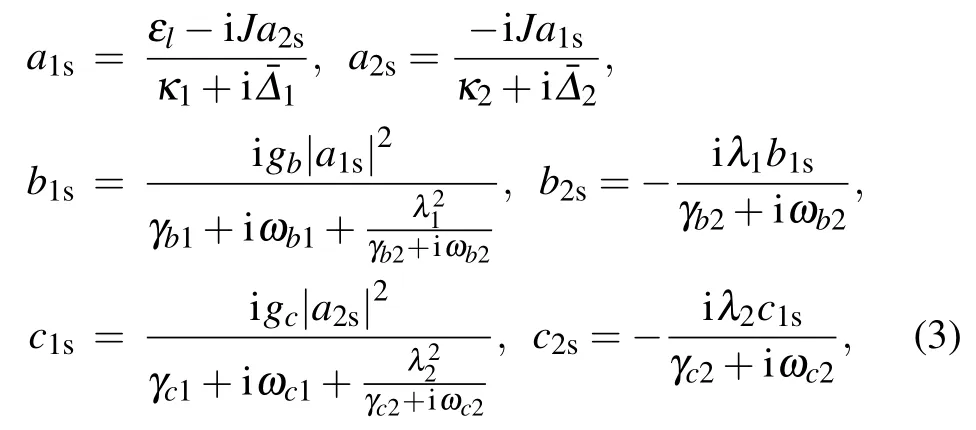
Up to now, most experimental realizations of cavity optomechanics are still in the single-photon weak coupling limit.[1]We ignore the high order terms of the fluctuation part,and the linearized quantum Langevin equations can be written as

where G1=gba1sand G2=gca2sare the effective optomechanical coupling rate between optical mode a1(a2) and the corresponding mechanical mode b1(c1). As the steady-state mean values a1sand a2scan be obtained by Eq.(3),we have

Now,we study the transmission of a weak-probe field through an optomechanical system. Employing the input-output relation[49]

we redefine the output field as

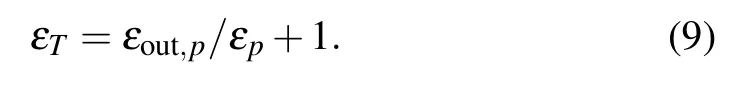
According to the knowledge of the absorption and dispersion,it is clear that the real part vp=Re(εT) and the imaginary part up=Im(εT)denote the absorption and dispersion of the probe field,[34]respectively. The quadratures can be measured via the homodyne technique.[49]

3. Numerical results and discussion

In the following part,we choose the experimental parameters to calculate the transmission spectrum of cavity a2to the probe field. To simplify,we chose gb=gc=g,λ1=λ2=λ,and γb1=γb2=γc1=γc2=γm. In a realistic cavity optomechanical system comprising of an optical cavity and a mechanical resonator,[22]these parameters are: ωm/2π =51.8 MHz,γm/2π = 141 Hz, κ1/2π = 0.2 MHz, κ2/2π = 15 MHz,J/2π =15 MHz, g/2π =5 kHz, Pl=5 mW,λc=1064 nm,and the coupling strength between two interacting mechanical modes λ/2π =5 MHz, which is slightly larger than the one given in Refs.[24,37].

In Fig.2,we simulate the absorption(vp)and dispersion(up)of the probe field with the effective detuning ω/ωm.From Fig.2(a), we can see that five transparency windows emerge from the absorption spectrum of the probe field in the presence of the coupling strength λ and g. The five transparency windows show that the hybrid optomechanical system becomes simultaneously transparent to the probe field at five different frequencies. The emergence of multiple OMIT windows in the hybrid optomechanical system can be understood analytically through inspecting the structure of the output field. From Eq. (7), we can see that the denominator becomes the fifth power in ω,so it has at most five different roots,which corresponding to five transparent windows.

Fig.2. The absorption vp (solid line)and dispersion up (dashed line)as a function of detuning ω/ωm. With the parameters(a)g/2π =5 kHz,λ/2π = 5 MHz; (b) λ = 0 Hz, g/2π = 5 kHz; (c) g = 0 Hz. For all plots, ωm/2π =51.8 MHz, γm/2π =141 Hz, κ1/2π =0.2 kHz,κ2/2π =15 MHz,J/2π =15 MHz,Pl =5 mW,and λc=1064 nm.

When the coupling between two resonators is switched off,i.e. ,λ =0,the term εTis The behavior of the probe field becomes triple-OMIT, which is the same as the transparency induced by a two-cavity-tworesonator optomechanical system.[35]Its real and imaginary parts are shown in Fig.2(b). Obviously,the disappearance of the coupling strength λ causes two transparency window to disappear.

Next, when the coupling between the cavity and the resonator is switched off,i.e.,g=0,the form of the εTbecomes

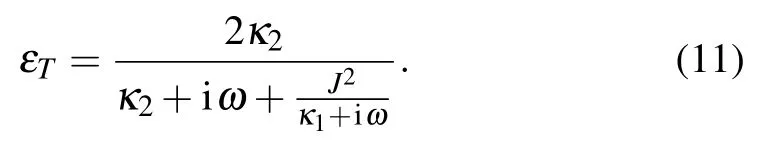
We can see that Eq.(11)has the standard form of the spectral response for OMIT, and the behavior of the probe field becomes the single coupled resonator-induced transparency.[50]Without any mechanical driving,a standard single OMIT in a two-cavity system emerges around the resonance point ωm=0,see Fig.2(c).

The origin of the five-OMIT windows can also be revealed by the quantum interference effect between different energy level pathways, and the effective energy structure for the hybrid system is shown in Fig.3. For a coupled twocavity system(i.e.,g=0),the normal optical mode splits into two modes and the single transparency window of the output field appears, which is based on the destructive interference effect.[51]If g/=0 and λ =0,the resonators b1and c1are coupled to the cavity a1and a2via optomechanical interaction,respectively.The additional optomechanical coupling will break down the two symmetry of the EIT-like level,[35]where the single transparency window is split into three windows.Moreover, when the coupling between the resonator b1and b2, as well as c1and c2is present, the energy level of each original mechanical resonator is split into two new dressed levels b+(c+)and b−(c−). The quantum interference between different energy level pathways occurs,which means five transparency windows appear,and the relevant mechanisms have been studied extensively.[38,45]

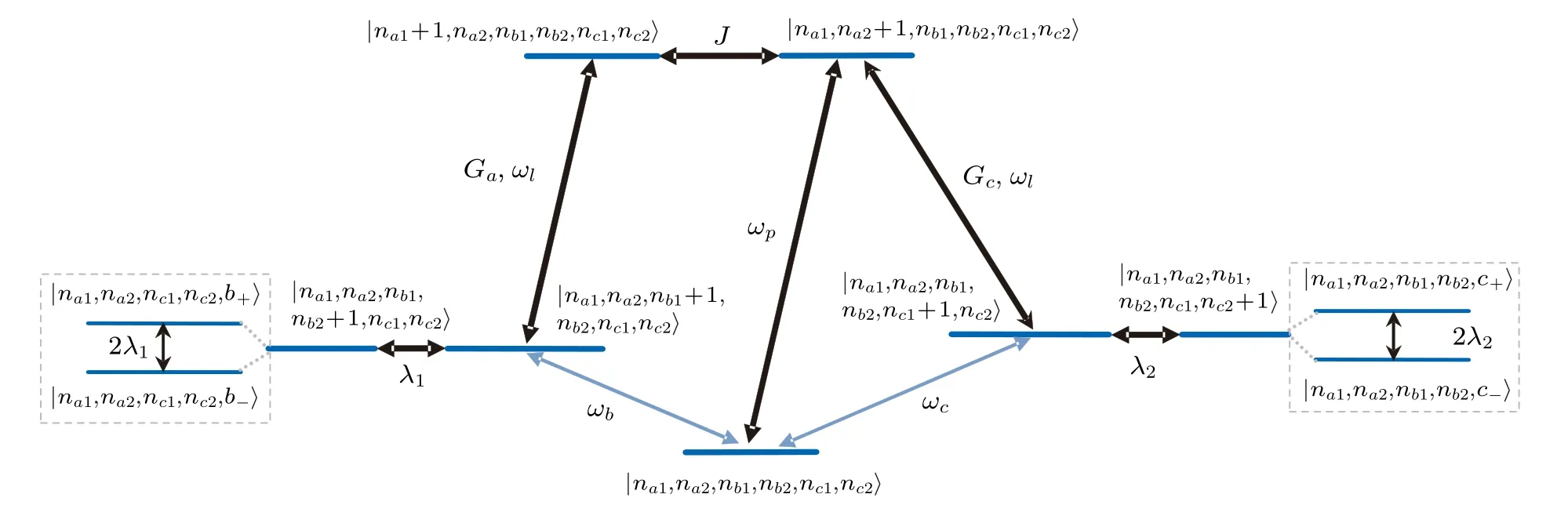
Fig.3. Energy-Level diagram of the total system with ωb1=ωb2=ωc1=ωc2=ωm and the coupling strength λ1=λ2=λ /=0 and g1=g2=g/=0. |ni〉(i →a1,a2,b1,b2,c1,c2)denotes the number state of each cavity modes and mechanical modes,respectively.

4. Tunable multiple-OMIT controlled by system parameters

To further explore the multiple-OMIT properties,we plot the absorption spectrum vpas functions of ω/ωmand the classical driving power Pl, as well as the coupling strength λ, as shown in Fig.4. Here,the effect of the coupling strength J between two cavities on transparency windows is not described,because it has been studied in detail in Refs. [7,35,38]. In Fig.4(a),we plot the absorption of the probe field for different values of the classical driving power Pl. For the classical driving power Pl=0,which means that there is no classical driving in the hybrid system,the absorption spectrum is the single OMIT in the standard two-cavity system.[31]With the increase of the classical driving power Pl,the effective coupling G1and G2are not equal to zero from Eq.(5),the correlation is established between the cavity a1(a2)and the oscillator b1(c1)as well the oscillator b1(c1) and the oscillator b2(c2), and the interference path is increased from one to five. As a result,the absorption spectrum exhibits five transparency windows. The existence of the classic driving power Plinduces the splitting effect. The larger the Pl,the wider the transparency windows besides the middle one,the larger the separation between outermost transparent points.

Fig.4. The absorption vp as functions of ω/ωm and (a) the classical driving power Pl, (b)the coupling coefficient λ. The other parameters are the same as in Fig.2.

Figure 4(b) presents the variation of the absorption vpwith ω/ωmfor different coupling strengths λ between two oscillators. By choosing the same parameters except for the values of λ as in Fig.2(a),we obtain Fig.4(b). For λ =0 Hz,the absorption spectrum is the triple-OMIT,and the middle dip locates at ω =0.[35]For the case of λ /=0 Hz,it is interesting that we can get five OMIT because of the dressed mechanical modes formation,and the middle window splits into three from Fig.4(b). Once λ exists, the coupling between the two mechanical oscillators is established, and the mode splitting effect of the coupling of the two oscillators appears, which can be seen from Fig.3. In addition,with the increasing of the coupling parameter λ,the width of the middle three windows increases,[27]and the two outermost transparency windows are further and further.

Fig.5. The separation d (units of ωm =2π×51.8 MHz) between the minima of the two outermost dips in the absorption spectrum as a function of: (a)the classical driving power P(units of Pl =5 mW);(b)the coupling strength λ (units of λ0=2π×5 MHz). Other parameters take the same values as in Fig.2.

In order to verify that the separation between the two outermost windows is affected by the classical driving power Pland the coupling strengths λ,we draw Fig.5.The two minima of absorption in Fig.5 can be evaluated by

here, the detunings ωmax+and ωmin−are the points with absorption minima. As a result, the separation of the outmost minima is d =|ωmax+−ωmin−|. Figures 5(a) and 5(b) show that the separation d between the two maxima increases almost linearly with increasing Pland λ. The conclusion is consistent with the performance in Figs.4(a)and 4(b). So,we can draw a conclusion that the multiple-OMIT can be tuned by the classical driving power Pland the coupling strength λ.

5. Conclusion

In summary, we have investigated the optomechanically induced transparency in two distant optomechanical systems.The presence of coupling strength between two oscillators causes five transparent windows in the optomechanical system.If the coupling strength λ or g is vanishing,the number of the transparent windows will be reduced to three or one.In addition,we have also investigated the influence of various factors on multiple-OMIT, including the classical driving power Pland the mechanical coupling strength λ. We observe that the width and the transparent point of the five windows can be controlled by the classical driving power Pland the coupling strength λ,respectively. The larger the Pland λ,the wider the transparent windows, and the further the separation between the two outermost windows. This result can be extended to multi-cavity systems, where the storage, transportation, and control of light are in prospect.