Dissipative dynamics of an entangled three-qubit system via non-Hermitian Hamiltonian: Its correspondence with Markovian and non-Markovian regimes
2021-03-19RastegarzadehandTavassoly
M Rastegarzadeh and M K Tavassoly
Laser and Optics Group,Faculty of Physics,Yazd University,Yazd 89195-741,Iran
Keywords: non-Hermitian Hamiltonian,entanglement,concurrence measure,Markovian and non-Markovian regimes
1. Introduction
Quantum entanglement, as a marvellous phenomena in quantum optics and quantum mechanics, has been utilized in quantum information science and technologies.[1-5]The dissipation as a source of entanglement attenuation,which destroys quantum coherence, has been converted to the most important and ubiquitous topics in quantum optics of open quantum systems. Dissipative systems have been investigated with different approaches.[6-8]Among them we may refer to density operator(the Lindbland master equation), quantum jump and noise operator approach.[9]In the studies on the interaction of quantum optics systems with their environments, two main regimes are considered, known as Markovian and non-Markovian. The quantum Fisher information flow may be employed for distinguishing the Markovian and non-Markovian processes.[10,11]Moreover,in particular,the entanglement revives in the non-Markovian regime[9,12-15]and reduced exponentially in the Markovian regime.[16-18]In fact,even though Markovian dynamics includes a level of back reaction, it neglects the entanglement that arises between bodies and bath modes during the evolution. Although some works deal with this issue,[19]it is an attractive theoretical challenge to extend the obtained results under various conditions in the Markovian to the non-Markovian regime.[20]
Along the above-mentioned approaches, the non-Hermition Hamiltonian approach is a rather different method which has been frequently used in the literature deal with open quantum systems[21-26]and PT-symmetric systems.[27,28]Also, a few applications of non-Hermitian Hamiltonian in quantum optics have been established in Ref. [29]. According to the theory of quantum jump,whenever no detector click occurs, the system dynamics follows a non-unitary evolution(which governs via a suitable non-Hermitian Hamiltonian[7]).For further usefulness of non-Hermitian operators in quantum optics studies, one may refer to Ref. [30]. Related to the latter approach, in Ref. [21], non-Hermitian Hamiltonian for a modulated Jaynes-Cummings model has been studied.The entropy of “single-qubit” is evaluated by considering a general non-Hermitian Hamiltonian.[22-24]Also, the authors in Ref. [25] investigated the evolution of quantum (von Neumann)entropy and entropic uncertainty of an entangled“twoqubit”system in which only one of the two qubits is affected by the environment described via a non-Hermitian Hamiltonian.
Moreover, as is found in the literature, extending twopartite systems to three-and more-partite systems is of enough interest for their usefulness applications. For instance, quantum teleportation protocols, based on three-qubit (or in general multi-qubit) entangled states, are widely used in order to construct quantum networks in the theoretical[31-34]and practical[35-37]researches, especially for their applications in the content of weak measurement and quantum measurement reversal.[38-40]As an example,the extension of entanglement in superconducting circuits, which has been so far limited to two qubits, to three, eight and ten qubits has been achieved among spins,ions and photons,respectively.[41]
Motivating by the above-mentioned facts, in the present work we study the entanglement dynamics of an entangled“three-qubit”system in the presence of dissipation via extending the presented approach in Refs. [25,26], wherein a twoqubit system is considered (one of them is interacted with its environment and the other one is isolated), and a non-Hermitian Hamiltonian is used. In detail, we assume three entangled qubits, where only one of them interacts with the environment via a non-Hermitian Hamiltonian and the other two qubits have been isolated. Our aim is to investigate the entanglement time behavior of each pair of qubits. To achieve our purpose, we obtain the temporal evolution of the density matrix of the entire system via applying time evolution operator on the two initial states, in the cases of pure and mixed initial density matrices. Then, we calculate the reduced density matrix associated with all possible qubit pairs of the three qubits. In the continuation, we evaluate the dynamics of entanglement of the three possible qubit pairs via the concurrence measure for deferent initial conditions,either with pure or mixed initial states. As a further interesting result of this work, we will establish a suitable correspondence between the considered dissipative model with the Markovian and non-Markovian regimes by introducing a critical value for the dissipative parameter in the considered non-Hermitian Hamiltonian approach.
The rest of the paper is organized as follows:In Section 2,we present our model and investigate its evolution. In Section 3, we investigate the evolution of entanglement among three considered qubits when the system is initially prepared in pure as well as in mixed states. Finally,we provide our concluding remarks.
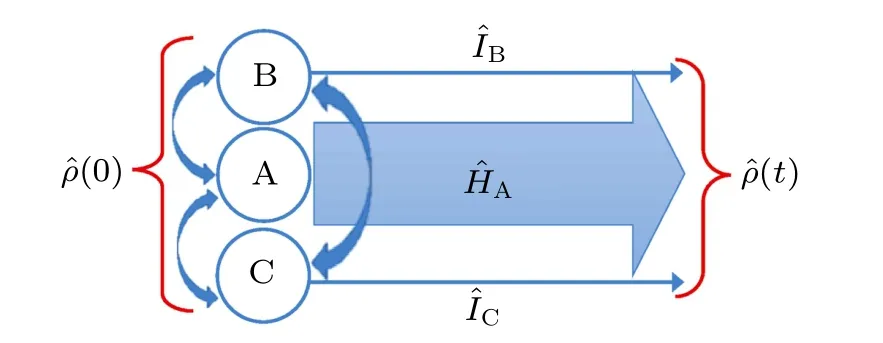
Fig.1. Diagram of the entangled three-qubit system under the influence of environment.
2. The model and its evolution
We assume an entangled three-qubit system where the qubit A, with ground (excited) states |0〉A(|1〉A) experiences a local environmental effect described by a non-Hermitian Hamiltonian,while the other two qubits B and C,with ground(excited) states |0〉B(|1〉B) and |0〉C(|1〉C), are isolated (see Fig.1). The general form of the non-Hermitian Hamiltonian ˆHAis written as

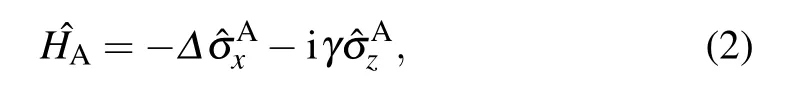
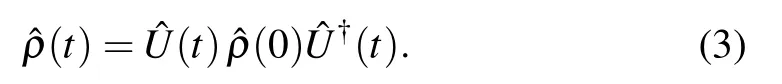

By straightforward calculations,we achieve the matrix corresponding to the time-evolution operator of qubit A as follows:
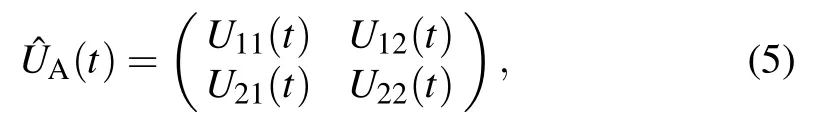
with elements
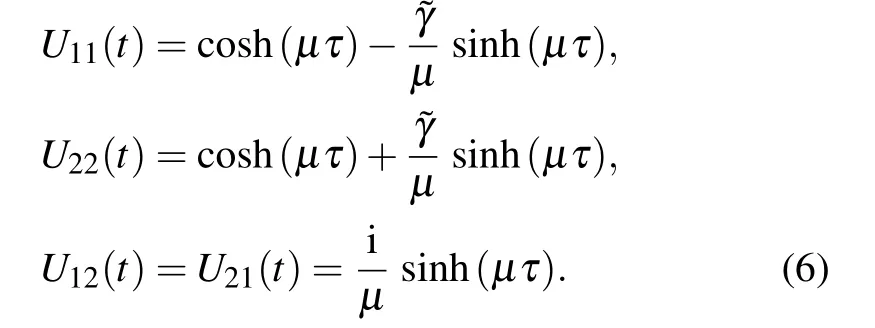

3. Entanglement of the system in the absence and presence of dissipation
3.1. The concurrence for the initial pure state
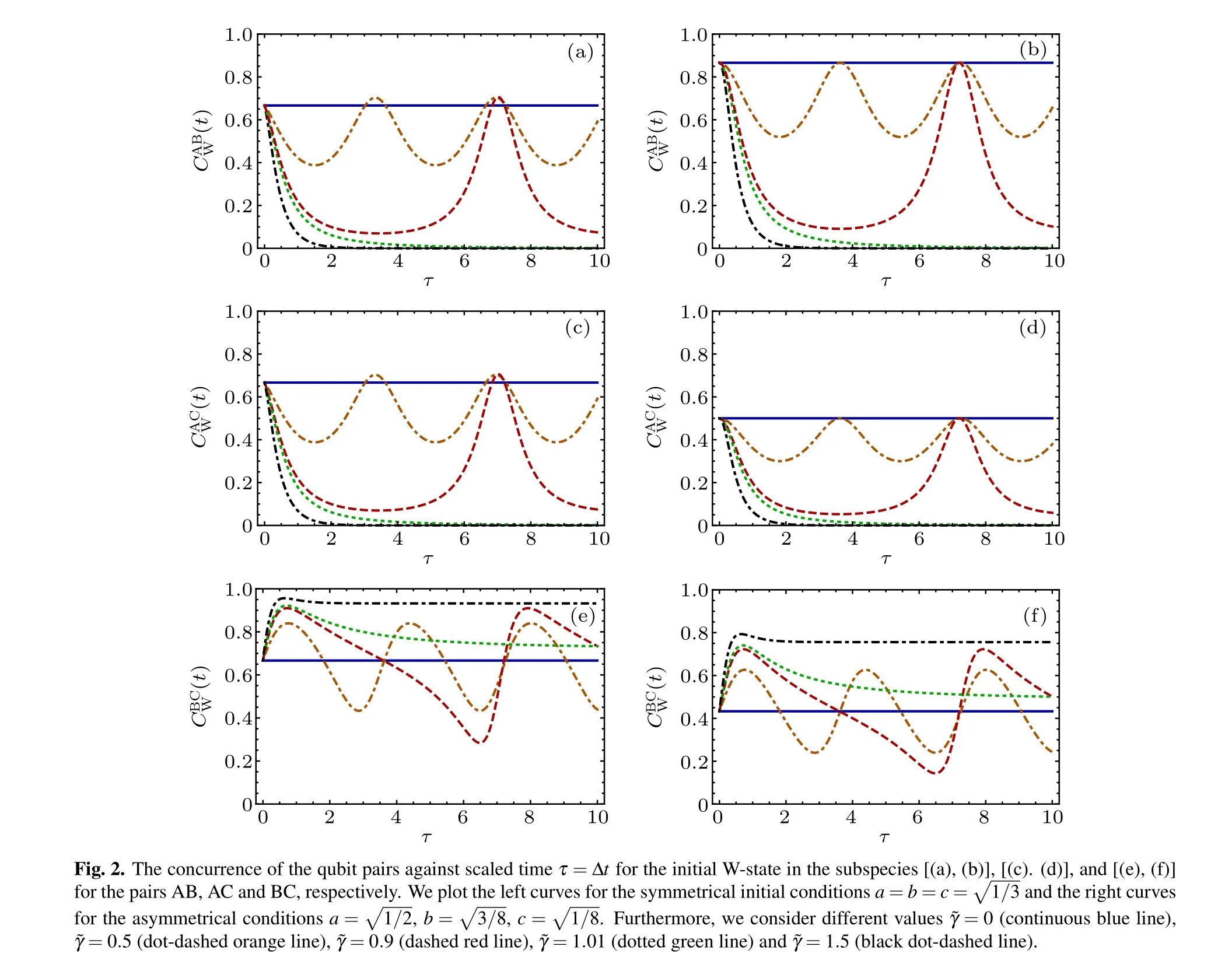
At this stage,we assume that the three-qubit system is initially prepared in two pure states,i.e.,the generalized Schmidt decomposition as Werner state (W-state)[42]as well as the generalized Greenberger-Horne-Zeilinger (GHZ) state[43,44]as follows:

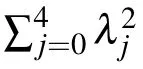
Therefore,we have

Using Eqs. (3), (4), (5), (7) and (8), and after some lengthy calculations, the explicit form of the density operator of the system can be obtained. As a result, the reduced density matrices can be calculated by

Here,we represent only one of the above reduced density matrices(ρAB)for the above introduced initial states in Eqs.(7)and(8):
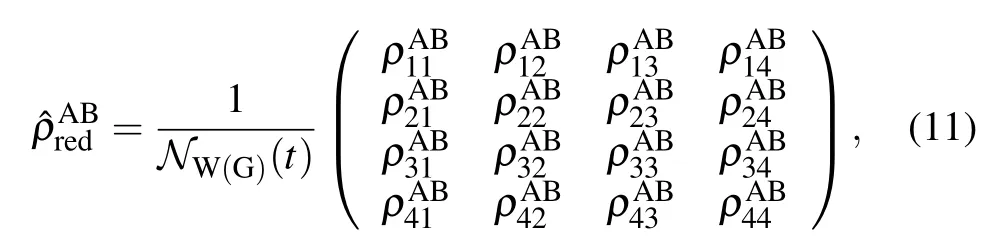
where NW(G)(t)is the normalization factor that reads
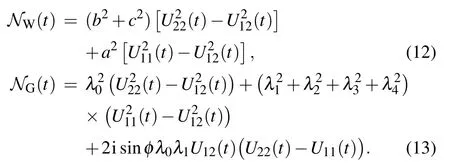
The matrix elements in Eq. (11) for the initial W-state are given by

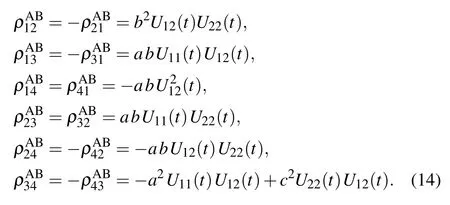

Also,we have obtained the concurrence measure for all three pairs of qubits AB, AC and BC in the following form, when we consider the GHZ-state(8)as the initial state of the system,
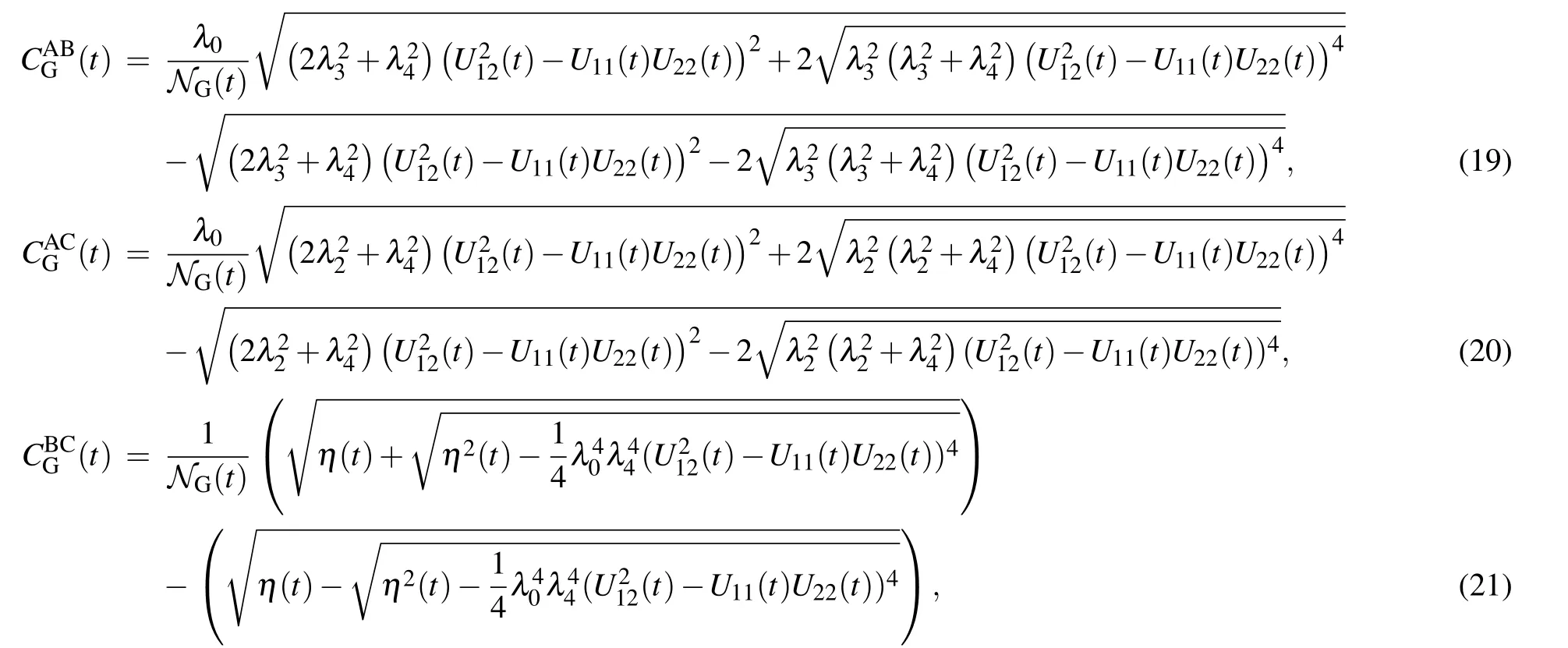
where we have defined



3.2. The concurrence for the initial mixed state
Here we suppose that the initial state of the system is prepared in ensembles of states|Ψ〉1and|Ψ〉2with classical probabilities w1and w2, respectively. Thus, the density operator describing the entire system can be written as
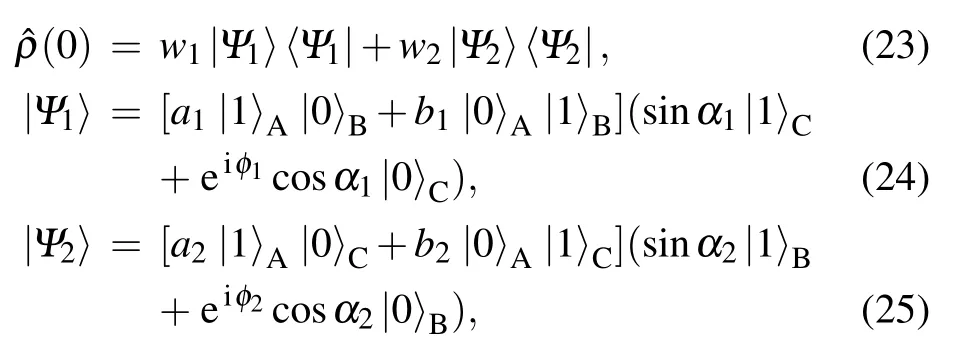


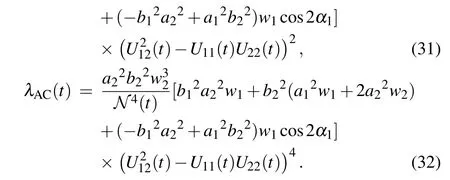


3.3. The von Neumann entropy for the initial pure and mixed states
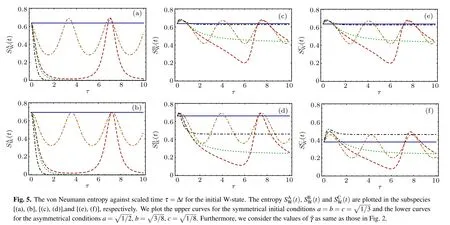
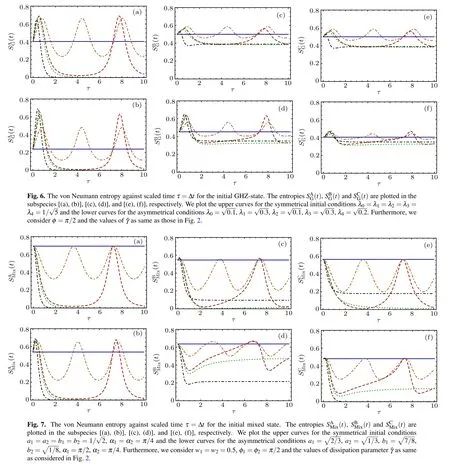
Now,we investigate the entanglement between each qubit A, B or C with other parts of the system using the von Neumann entropy which is defined as

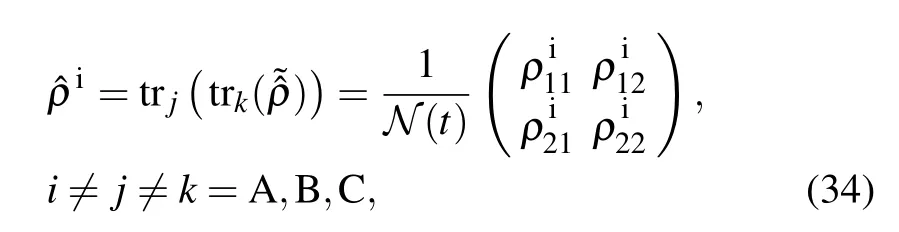
where N(t) is the normalization factor that can be obtained according to Eqs. (12), (13) and (29) for the initial W- and GHZ-state as well as a mixed state, respectively. For the initial W-state the relevant matrix elements read

Similarly,for GHZ-state one has
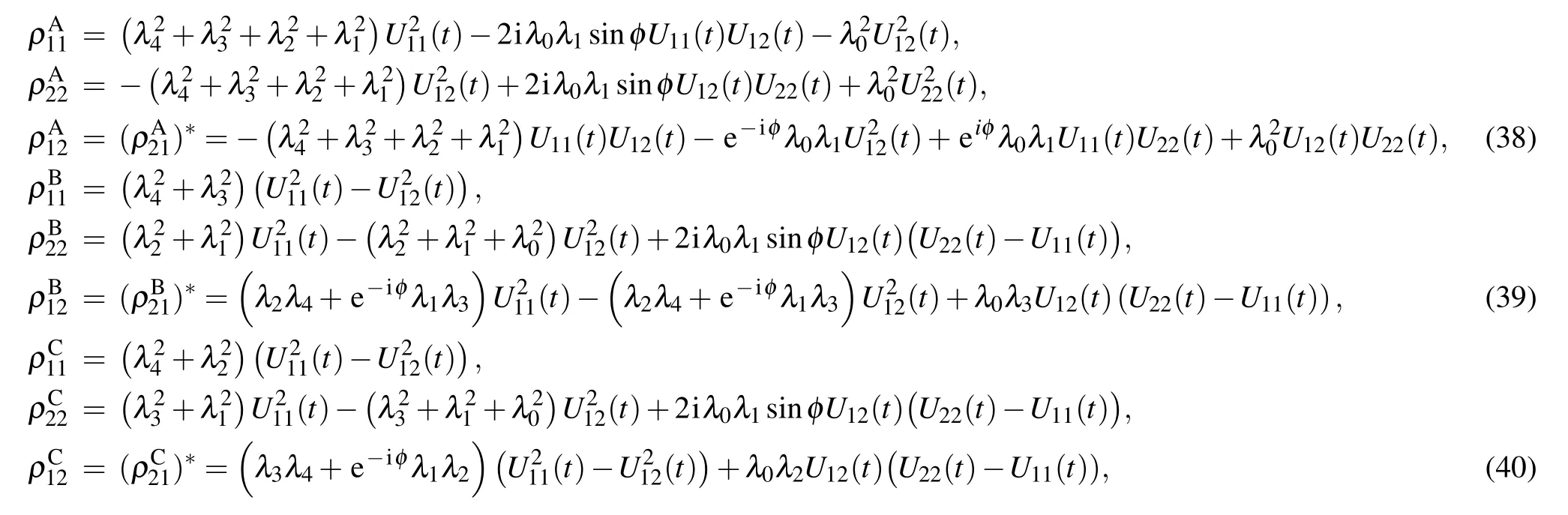
and for the mixed initial state one has


4. Summary and conclusions
We have used the non-Hermitian Hamiltonian approach to study the dynamical behavior of entanglement between each pairs of three entangled qubits (only one of the qubits interacts with its environment)in the presence of dissipation. For this purpose, we obtain the time evolution of the density matrix after applying the time evolution operator on the pure as well as mixed initial density matrices associated with the three qubits. Then, we calculate the reduced density matrix corresponding to each pair of qubits and subsequently we evaluate the concurrence measure and von Neumann entropy, numerically. In general,comparing to Ref.[25],we have generalized the presented model given in Ref.[25]in two aspects: (i)We have extended the model in Ref. [25] to three qubits which are initially prepared in pure and mixed entangled state (one of the qubits affected by environment and the other two qubits are isolated from the environment) instead of only two (initially entangled)qubits(one affected by environment and the other qubit is isolated in Ref. [25]). (ii) Also, we investigate the entanglement between qubit pairs by concurrence measure while in Ref. [25], the entanglement has been studied by the inappropriate measure. Indeed,we have investigated the influences of dissipation parameter on the entanglement of various pairs of qubits via the concurrence which is the most suitable measure for two qubit systems. Our numerical results for the pure and mixed initial states show that the concurrence and von Neumann entropy do not change for ˜γ=0,demonstrating the stability of entanglement between qubits in the absence of dissipation. Furthermore, the entanglement in two pairs of initially entangled qubits AB and AC monotonically decreases with increasing the strength of dissipation.This behavior has been characterized before for the Markovian regimes.Moreover, for ˜γ <1, some oscillations may be observed in the above mentioned subsystems which can correspond to the non-Markovian regimes. Thus, we may define ˜γ =1 as the critical dissipative value in our non-Hermitian approach, in which by controlling it one can arrive at a Markovian or non-Markovian regime. Also, for the entanglement between the pair BC, we observe that for the pure state the qubits B and C which have been initially isolated from the environment become entangled,while for initial mixed states this pair remains separable as time goes on.It is interesting to notice that the entanglement stability grows to values more than its initial value in the pair qubit BC for the pure state. Similarly,the evolution of the von Neumann entropy of qubits A,B and C are consistent with the Markovian and non-Markovian regimes for ˜γ >1 and ˜γ <1,respectively.
Appendix A
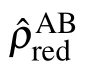

where N(t) is the normalization factor defined in Eqs. (13)and(29),corresponding to GHZ-state and mixed state,respectively. The matrix elements for GHZ-state may be obtained as follows:

and also,the matrix elements for the mixed initial state read

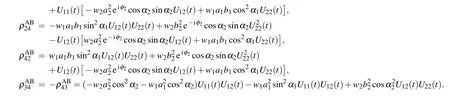
杂志排行
Chinese Physics B的其它文章
- Transport property of inhomogeneous strained graphene∗
- Beam steering characteristics in high-power quantum-cascade lasers emitting at ~4.6µm∗
- Multi-scale molecular dynamics simulations and applications on mechanosensitive proteins of integrins∗
- Enhanced spin-orbit torque efficiency in Pt100−xNix alloy based magnetic bilayer∗
- Soliton interactions and asymptotic state analysis in a discrete nonlocal nonlinear self-dual network equation of reverse-space type∗
- Discontinuous event-trigger scheme for global stabilization of state-dependent switching neural networks with communication delay∗
