Deterministic nondestructive state analysis for polarization-spatial-time-bin hyperentanglement with cross-Kerr nonlinearity∗

Hui-Rong Zhang(张辉荣), Peng Wang(王鹏), Chang-Qi Yu(于长琦), and Bao-Cang Ren(任宝藏)

Department of Physics,Capital Normal University,Beijing 100048,China

Keywords: quantum communication,deterministic nondestructive state analysis,polarization-spatial-time-bin hyperentanglement

1. Introduction

Entanglement is an useful quantum resource in quantum information processing, and it is a crucial resource for quantum communication programs, such as quantum key distribution,[1-7]quantum dense coding,[8,9]quantum teleportation,[10,11]quantum secret sharing,[12-15]quantum swapping,[16]quantum secure direct communication,[17-23]and so on. In these quantum communication programs,Bell state analysis (BSA) is a key step to read out the quantum information.[24-26]The entanglement in multiple degrees of freedom (DOFs) of a quantum system, called hyperentanglement,[27]has attracted widespread attention in recent years. For instance, there are polarization DOF, timebin DOF, spatial-mode DOF, frequency DOF, and orbital angular momentum DOF in photon system,and the hyperentangled states in polarization-frequency DOFs,[28]polarizationtemporal DOFs,[29]polarization-momentum DOFs,[30-32]polarization-momentum-temporal DOFs,[33]and polarizationorbital-angular-momentum DOFs[34]have been demonstrated in experiments.

Hyperentanglement has been used to assist deterministic two-photon Bell state analysis,[35,36]quantum error-correcting,[37,38]quantum cryptography,[39,40]quantum repeater,[41]entanglement purification,[42-45]and so on. With the high capacity property of hyperentanglement,the channel capacity of quantum communication can be increased, such as its applications in measurement-deviceindependent quantum secure direct communication (MDIQSDC),[46,47]measurement device-independent quantum key distribution(MDI-QKD),[48]hyperdense coding,[49]quantum hyperteleportation,[50,51]hyperentanglement swapping,[52]hyperentanglement purification,[53-55]and hyperentanglement concentration.[56,57]Hyperentangled state analysis is a key step to read out the quantum information in the high-capacity quantum communication protocol. Many hyperentangled Bell state analysis (HBSA) schemes have been proposed to discriminate the hyperentangled Bell states,which show that the hyperentangled Bell states are difficult to be determinately discriminated using linear optics.[49,58-60]Assisted by the auxiliary momentum entanglement and time-bin DOF, the polarization-momentum hyperentangled Bell states can be discriminated determinately with linear optics,[61]and the complete polarization-momentum HBSA can also be implemented using auxiliary hyperentanglement.[62]However, the applications of HBSA will be limited by using auxiliary entanglement of other DOFs of photon system.

The applications of deterministic HBSA can be broadened by introducing nonlinear optical elements,[50,52,63-67]where the auxiliary entanglement of other DOFs of photon system is not required. In 2010, Sheng et al.[50]proposed the complete HBSA for polarization-spatial DOFs of photon system with quantum nondemolition detector(QND),resorting to cross-Kerr nonlinearity. This method can be generalized to complete hyperentangled Greenberger-Horne-Zeilinger(GHZ)state analysis.[68]Subsequently,some works showed that the complete HBSA for polarization-spatial DOFs of photon system can also be implemented by QND using cavity quantum electrodynamics.[52,64]In 2016, Li and Ghose presented two efficient self-assisted complete HBSA schemes for polarization-spatial DOFs[65]and polarizationtime-bin DOFs[66]of photon system respectively, which can reduce the number of QND used in complete HBSA.Recently,Cao et al.[67]showed that the function of QND can be replaced by a quantum swap gate for the polarization states of two photons in the complete HBSA for polarization-spatial DOFs of photon system.

Besides the HBSA for two DOFs of photon system, the HBSA for six-qubit three DOFs of photon system has also attracted much attention. In 2016, Liu et al. presented a complete nondestructive HBSA scheme for two-photon system hyperentangled in two longitudinal momentum DOFs and the polarization DOF with the help of cross-Kerr nonlinearity,where the 64 hyperentangled Bell states can be completely distinguished without destruction.[69]In 2018, Wang et al. gave a deterministic HBSA scheme for polarization-spatial-time-bin DOFs of photon system with cross-Kerr nonlinearity.[70]In this scheme, the path coupler is used to erase the path information of the photon, and the hyperentangled Bell states are destructed after the HBSA process.

In this paper, we present a deterministic nondestructive HBSA scheme for polarization-spatial-time-bin DOFs of photon system using cross-Kerr nonlinearity, where the hyperentangled Bell states in three DOFs are preserved after the HBSA process.In the scheme,polarization parity-check QND(P-QND)and spatial-mode parity-check QND(S-QND)constructed by the cross-Kerr nonlinearity are the core elements for determinately distinguishing polarization Bell states and spatial-mode Bell states, respectively. For the time-bin Bell states analysis, we introduce the swap gate for polarization state and time-bin state of a photon (P-T swap gate) to swap the Bell states of polarization and time-bin DOFs. By transforming the time-bin information to the polarization state,the information in time-bin Bell states can be determinately distinguished using P-QND. Moreover, the Bell states analysis for one DOF will not destruct the Bell states of other two DOFs,so the hyperentangled Bell states in the three DOFs are preserved after the HBSA process. This deterministic nondestructive HBSA scheme may have useful applications in many quantum information protocols in the future, such as in MDI-QSDC,MDI-QKD,blind quantum computation,and distributed quantum computation.

2. Deterministic nondestructive analyzer for hyperentangled Bell state in three DOFs

The two-photon polarization-spatial-time-bin hyperentangled Bell state can be expressed as

Here, |ΩP〉ABrepresents one of the four polarization Bell states,and the four polarization Bell states are expressed as

|ΠS〉ABdenotes one of the four spatial-mode Bell states, and the four spatial-mode Bell states are expressed as

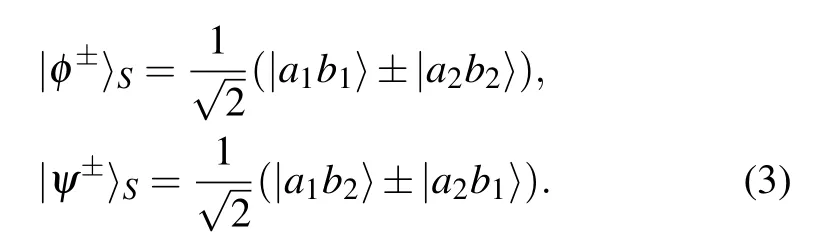
|ΛT〉ABmeans one of the four time-bin Bell states,and the four time-bin Bell states are expressed as

Here, the subscripts A and B indicate two photons, and the subscripts P,S,and T indicate polarization,spatial mode,and time bin DOFs, respectively. |H〉 and |V〉 are the horizontal and vertical polarization states of the photon. Photon A (B)has two spatial modes|a1〉and|a2〉(|b1〉and|b2〉). |S〉and|L〉are two different time bins,where|S〉represents the early time bin and|L〉represents the late time bin. Considering the three DOFs together, there are 64 polarization-spatial-time-bin hyperentangled Bell states. In this section, we show that the 64 hyperentangled Bell states can be analyzed deterministically without being destructed.

2.1. Deterministic analysis of polarization Bell states

Fig.1. (a) Schematic diagram of the quantum nondemolition detector for polarization parity check(P-QND)with the cross-Kerr nonlinearity,which is used to distinguish even-parity polarization Bell states |φ±〉P from odd-parity polarization Bell states|ψ±〉P. Polarizing beam splitter (PBSi, i=1,2,3,4) is used to transmit the horizontal polarization state |H〉 and reflect the vertical polarization state |V〉. When a photon passes through the nonlinear cross-Kerr media,the weak cross-Kerr nonlinearity puts a phase shift θ (or −θ) on the coherent probe beam|α〉. Half-wave plate (HWP45) performs bit flip operation on the polarization state of a photon, i.e., |H〉⇔|V〉. |x〉〈x| is the homodyne measurement that can distinguish different phase shifts. (b)Schematic diagram of polarization Bell state analyzer. Half-wave plate(HWP22.5)performs a Hadamard operation on the polarization state of a photon.

After the two photons A and B pass through the circuit of P-QND shown in Fig.1(a),the state of the system consists of two photons AB and the coherent state is evolved to Then the coherent state is measured by the X-quadrature measurement, and the polarization parity information is distinguished. If the coherent state has no phase shift, the polarization Bell state is one of the even-parity states |φ±〉P. If the coherent state has a phase shift(±θ),the polarization Bell state is one of the odd-parity states |ψ±〉P(the X-quadrature measurements do not distinguish phase shifts differing in sign“±”). Therefore, the four polarization Bell states can be divided into two groups using P-QND,i.e.,even-parity polarization Bell states |φ±〉Pand odd-parity polarization Bell states|ψ±〉P.

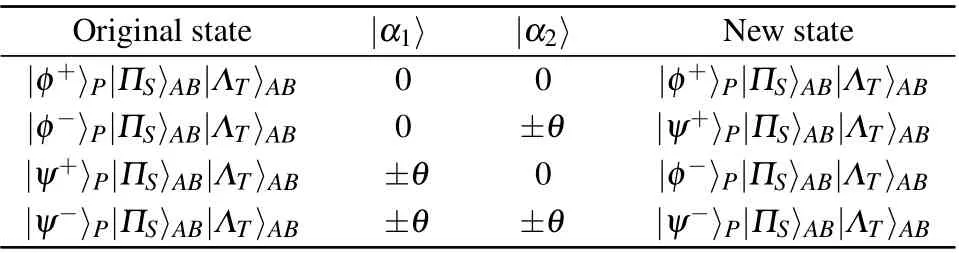
Table 1. Relationship of the original polarization Bell state, the new polarization Bell state after analysis process,and the two phase shifts of the coherent beams. |α1〉(|α2〉)represents the coherent state of the first(second)P-QND.

2.2. Deterministic analysis of spatial-mode Bell states

The scheme for deterministic analysis of spatial-mode Bell states is shown in Fig.2. The core element of this step is the quantum nondemolition detector for spatial-mode parity check(S-QND),and it consists of the nonlinear cross-kerr media and coherent probe beam. After the photons AB pass through the S-QND consisted of nonlinear cross-kerr media and coherent state |α1〉, the state of the system consisted of two photons AB and coherent state|α1〉is evolved to

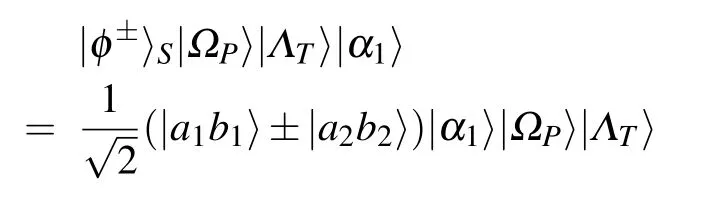
Then the coherent state is measured by the X-quadrature measurement, and the spatial-mode parity information is distinguished. If the coherent state has no phase shift, the spatialmode Bell state is one of the even-parity states |φ±〉S. If the coherent state has a phase shift (±θ), the spatial-mode Bell state is one of the odd-parity states |ψ±〉S(the X-quadrature measurements do not distinguish phase shifts differing in sign“±”). Therefore, the four spatial-mode Bell states can be divided into two groups using S-QND,i.e., even-parity spatialmode Bell states|φ±〉Sand odd-parity spatial-mode Bell states|ψ±〉S.

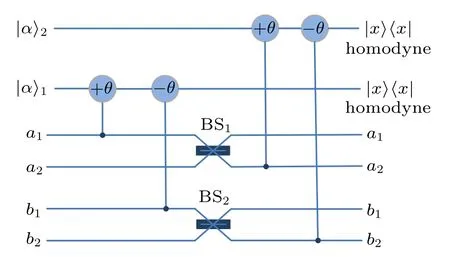
Fig.2. Schematic diagram of deterministic analysis of spatial-mode Bell states. It consists of two quantum nondemolition detectors for spatial-mode parity check (S-QNDs) and two 50:50 beam splitters(BSs). S-QND consists of the nonlinear cross-kerr media and coherent probe beam |α1〉 (or |α2〉). BS implements a Hadamard operation on the spatial-mode state of a photon,i.e.,|y1〉→(|y1〉+|y2〉),|y2〉→(|y1〉−|y2〉).

Subsequently, the two photons AB pass through 50:50 beam splitters(BSs),where the 50:50 BS performs Hadamard operation on the spatial mode state of a photon

Here y represents a or b. After the photons pass through 50:50 BSs as shown in Fig.2, the spatial-mode Bell states have the evolutions as follows: |φ+〉S→|φ+〉S, |φ−〉S→|ψ+〉S,|ψ+〉S→|φ−〉S, and |ψ−〉S→|ψ−〉S. In other words, evenparity spatial-mode Bell states |φ+〉Sand |φ−〉Sare evolved to|φ+〉Sand|ψ+〉S,respectively,and odd-parity spatial-mode Bell states|ψ+〉Sand|ψ−〉Sare evolved to|φ−〉Sand|ψ−〉S,respectively. Then the two photons pass through the second SQND consisted of the nonlinear cross-kerr media and coherent probe beam|α2〉,and the two original spatial-mode Bell states in the even-parity (odd-parity) group can be distinguished by the phase shift of the coherent state in the second S-QND.Now the four spatial-mode Bell states can be determinately distinguished as shown in Table 2. The relationship of the original spatial-mode Bell state, the new spatial-mode Bell state after analysis process, and the phase shifts of the two coherent beams is shown in Table 2.

Table 2. Relationship of original spatial-mode Bell state, the new spatial-mode Bell state after analysis process, and the phase shifts of the two coherent beams.

2.3. Deterministic analysis of time-bin Bell states

The scheme for deterministic analysis of time-bin Bell states is shown in Fig.3(b). The core element of this step is the swap gate for polarization state and time-bin state of a photon(P-T swap gate)as shown in Fig.3(a). The P-T swap gate consists of three controlled-not (CNOT) gates for polarization and time-bin states of a photon. The first CNOT gate consists of two PBSs and XT,which is used to perform bit flip operation on the time-bin state when the polarization state is|V〉. That is,

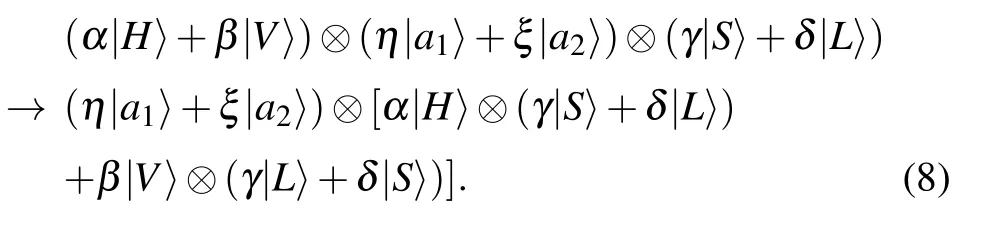
Here XTrepresents a bit flip operation on the time-bin state,which can be achieved using an active switch.[71]The second CNOT gate, using PCL(Pockels cell),[72]is used to perform bit flip operation on the polarization state when the time-bin state is|L〉. That is,

Then the photon passes through the third CNOT gate, which is the same as the first CNOT gate,and the single photon state is evolved as It is obvious that the polarization state and time-bin state of a photon are swapped after the photon passes through the P-T swap gate.

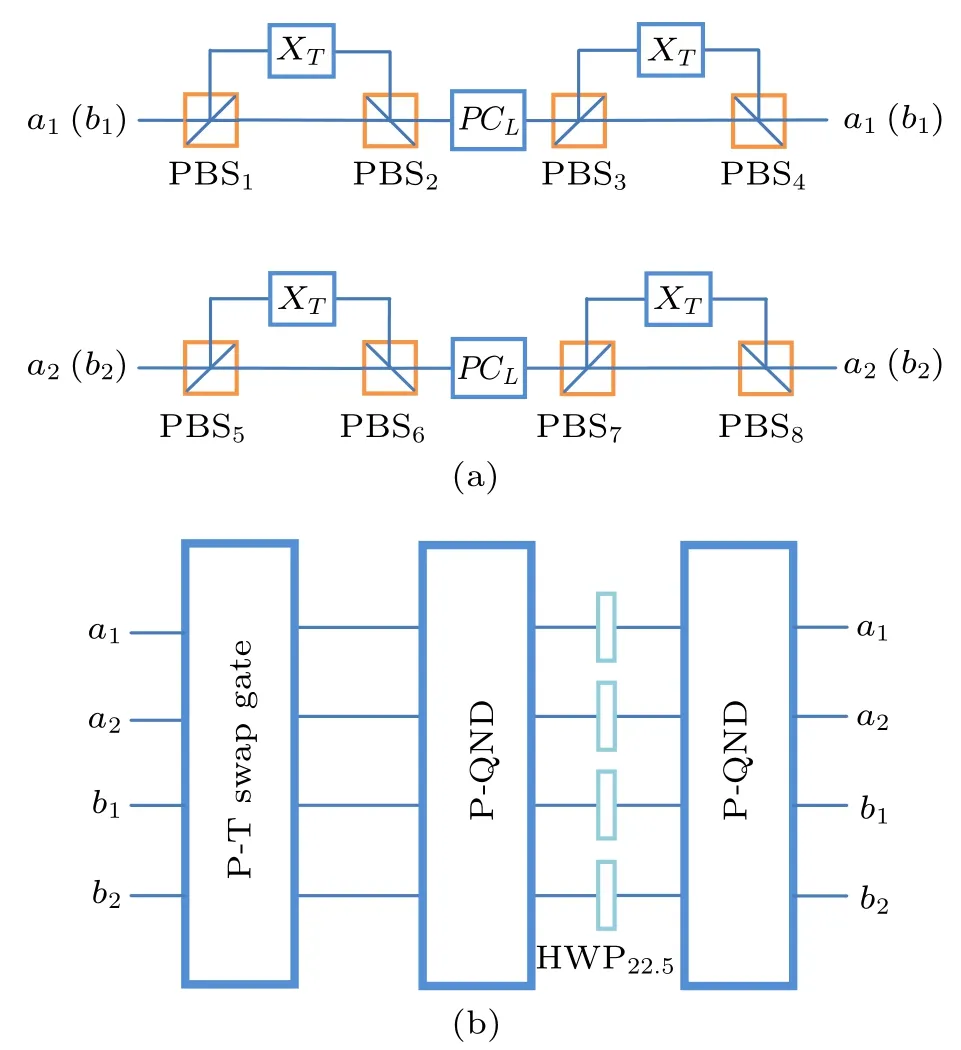
Fig.3.(a)Schematic diagram of the swap gate for polarization state and timebin state of a photon(P-T swap gate), which consists of three controlled-not(CNOT) gates. There are two CNOT gates composed of two PBSs and XT,which perform bit flip operation on the time-bin state if the polarization state is |V〉. XT implements a bit flip operation on the time-bin state. The CNOT gate using PCL performs bit flip operation on the polarization state if the timebin state is|L〉. (b)Schematic diagram of time-bin Bell state analyzer,which consists of P-T swap gate and P-QND.

Table 3. Relationship of the state before swap,the state after swap(after pass through the P-T swap gate in Fig.3(a)),and the phase shifts of two coherent probe beams. |α1〉(|α2〉)represents the coherent state of the first(second)P-QND.

After the two photons A and B pass through the P-T swap gate as shown in Fig.3(b), the polarization Bell state and the time-bin Bell state of the two-photon system AB will be swapped. For instance,the hyperentangled Bell state|ψ−〉P⊗|ψ−〉S⊗|φ+〉Twill be transformed to|φ+〉P⊗|ψ−〉S⊗|ψ−〉Tafter the two photons A and B pass through the P-T swap gate respectively, and the transformations of other hyperentangled Bell states are shown in Table 3. Now the original time-bin Bell state is transformed to polarization DOF, and it can be distinguished by the deterministic analysis of polarization Bell states introduced in Subsection 2.1 as shown in Fig.3(b). In Table 3, the four groups of hyperentangled Bell states correspond to four original time-bin Bell states, and they are determinately distinguished by the phase shifts of two coherent probe beams in P-QNDs of Fig.3(b).

3. Discussion and summary

We have presented a nondestructive deterministic HBSA scheme for six-qubit polarization-spatial-time-bin hyperentangled Bell states using cross-Kerr nonlinearity. The core elements of this scheme are P-QND,S-QND,and P-T swap gate.The P-QND(S-QND)is used to check the parity information of polarization (spatial-mode) Bell states, and the P-T swap gate is used to swap the polarization state and time-bin state of a photon. Using the three core elements, the 64 polarizationspatial-time-bin hyperentangled Bell states can be determinately distinguished without being destructed,resorting to the phase shifts of coherent probe beams in Tables 1-3. The relationship between the original hyperentangled Bell state and final hyperentangled Bell state is shown in Tables 1-3,where the final hyperentangled Bell state can be returned to the original hyperentangled Bell state by using polarization Hadamard operations,spatial-mode Hadamard operations,and P-T swap gates.For example,the original hyperentangled Bell state|φ−〉P|φ−〉S|ψ−〉Tis evolved to final hyperentangled Bell state |ψ−〉P|ψ+〉S|ψ+〉Tafter the nondestructive deterministic HBSA process,and the final hyperentangled Bell state can be returned to the original hyperentangled Bell state by performing spatial-mode Hadamard operations, P-T swap gates,and polarization Hadamard operations on two photons A and B successively.

In the previous polarization-spatial-time-bin HBSA,[70]the time-bin information is also transformed to the polarization DOF, but both the time-bin state and the spatial-mode state are erased by using the path coupler C[73-75]and unbalanced interferometer, which will destruct the hyperentangled state. In our work, we show that the time-bin information can be transformed to the polarization DOF without destroying the time-bin state and the spatial-mode state, resorting to PCL,XT,and linear optical elements. With this method,the 64 polarization-spatial-time-bin hyperentangled Bell states can be determinately distinguished without being destructed,which makes this scheme more useful and practical.

The core elements of this scheme (P-QND and S-QND)are constructed by the cross-Kerr nonlinearity,where the clean cross-Kerr nonlinearity at single-photon level is necessary in this scheme. In recent years, considerable progresses have been made on cross-Kerr effect.[76-82]For a weak cross-Kerr nonlinearity, the deterministic distinguishability between the shifted and non-shifted phases can be achieved by choosing a sufficiently large amplitude of the coherent state.[76]Moreover, a cross-Kerr phase shift of the cross-Kerr nonlinearity at single-photon level can be amplified to an observable value by using weak-value amplification,[77]and average cross-Kerr phase shifts can achieve 20 degrees per photon with both coherent microwave fields at the single-photon level using superconducting qubits.[80]These progresses indicate that this scheme may be realized with the experimental techniques in the near future.

In summary, we have proposed a deterministic nondestructive HBSA for hyperentangled state simultaneously entangled in polarization, spatial-mode, and time-bin DOFs of photon system. The polarization Bell states and spatial-mode Bell states are distinguished by P-QNDs and S-QNDs using cross-Kerr nonlinearity, respectively, and the time-bin Bell states are distinguished by P-T swap gates and P-QNDs,where the Bell states analyzer of one DOF will not destruct the Bell states of other two DOFs. Therefore,the polarization-spatialtime-bin hyperentangled Bell state can be preserved after the HBSA process. This nondestructive method may have important application in deterministic nondestructive analysis for hyperentangled GHZ states, and the P-QND and S-QND in this scheme can also be constructed with other kinds of nonlinear interactions. All these features make this deterministic nondestructive HBSA scheme more useful in quantum information protocols.