Hierarchical simultaneous entanglement swapping for multi-hop quantum communication based on multi-particle entangled states∗
2021-03-19GuangYang杨光LeiXing邢磊MinNie聂敏YuanHuaLiu刘原华andMeiLingZhang张美玲
Guang Yang(杨光), Lei Xing(邢磊), Min Nie(聂敏),Yuan-Hua Liu(刘原华), and Mei-Ling Zhang(张美玲)
School of Communications and Information Engineering&School of Artificial Intelligence,Xi’an University of Posts and Telecommunications,Xi’an 710121,China
Keywords: multi-hop quantum communication,entanglement swapping,teleportation,multi-particle
1. Introduction
Quantum entanglement plays a critical role in quantum computation and quantum communication, such as quantum teleportation,[1-3]quantum dense coding,[4-6]quantum key distribution,[7-9]and quantum secure direct communication.[10-12]In order to realize multi-user wide area quantum communication, the construction of quantum network has become the focus of attention.[13-15]However, it is difficult to distribute entangled particles between two remote users directly in a quantum network due to the inevitable losses on the quantum channel.
Entanglement swapping(ES)is an important method that can establish the entanglement path between two quantum users who do not share entanglement initially. The ES was first presented in 1993,[16]based on which,various multi-hop quantum communication schemes have been proposed.Cheng et al. devised a routing algorithm in wireless quantum networks by using the ES to construct the quantum bridge, and thus realizing the quantum teleportation.[17]Zhou et al. proposed a routing strategy for quantum internet,where quantum routers perform ES to establish entanglement connection.[18]The establishing rate of quantum path for point-by-point ES and segmentation ES was analyzed in Ref.[19]. Yu et al. proposed a two-end approximation algorithm based on ES in a wireless quantum network.[20]The similarity among the above schemes is that each intermediate node needs to perform ES hop by hop. As a result, the end-to-end time delay of entanglement establishment grows rapidly with the increase of the length and the hop count of a quantum path. We call this type of ES the sequential ES(SEQES).
In order to reduce the establishment delay of entanglement path in a wide area quantum network, Liu et al. proposed a three-hop simultaneous ES (SES) scheme, where all intermediate nodes simultaneously conducted Bell state measurements(BSM),and sent the measurement results to the destination node through classical channel.[21]Wang et al. proposed a teleportation scheme based on the SES in a multi-hop wireless quantum network.[22]The SES scheme was also applied to the bidirectional quantum teleportation, and the unitary operation to reconstruct the quantum state was obtained by solving the inverse matrix.[23]Gao et al. proposed a multihop W-state teleportation method based on multi-level binary tree networks with selective receiving nodes,and the nodes at all levels perform quantum measurement and result transmission simultaneously.[24]With the similar ideas, other multihop quantum information transmission schemes based on the SES were presented in Refs.[25-27].
However, in the above SES methods, each intermediate node should send the quantum measurement results to the destination node through classical channel,which would involve the forwarding of the classical information in each classical intermediate node along the classical channel, resulting in a very high classical transmission cost, so they are not suitable for large-scale quantum networks. On the other hand,the existing SES schemes mainly focus on the entanglement swapping of two-particle entangled states. As more powerful resources, multi-particle entangled states have been used in many novel quantum information tasks, including controlled teleportation,[28-30]bidirectional teleportation,[31-33]multiparty quantum secret sharing,[34-36]and multi-party quantum key agreement.[37-39]It is of great value to explore how to realize the multi-particle communication in a multi-hop quantum network rapidly and efficiently.
In this paper,we first put forward an SES scheme to establish the four-particle GHZ entanglement path, which is used to complete the multi-hop bidirectional teleportation of threeparticle GHZ states. Further, in order to reduce the classical information cost in SES scheme, we propose a hierarchical SES(HSES)scheme that is composed of level-1 SES and level-2 SES schemes, the former implements the inner segment entanglement swapping and the latter implements the inter segment entanglement swapping. Compared with the basic SES scheme,the HSES obtains a lower classical cost,and still shows a good time delay performance. The rest of the paper is organized as follows. In Section 2,we briefly introduce the process of bidirectional teleportation of three-particle GHZ states. In Section 3,we describe the details of SES scheme to establish the remote entanglement path for the bidirectional teleportation. In Section 4,we propose the HSES scheme. In Section 5,we analyze the performance of SES and HSES.Finally,the conclusions of our work are given in Section 6.
2. Bidirectional teleportation of three-particle GHZ states
In this section, we briefly introduce the scheme of the bidirectional teleportation of three-particle Greenberger-Horne-Zeilinger(GHZ)state,and the detailed process can be seen in Ref.[32]. It is supposed that Alice and Bob each have a three-particle GHZ state to be teleported to each other,which has the following form:
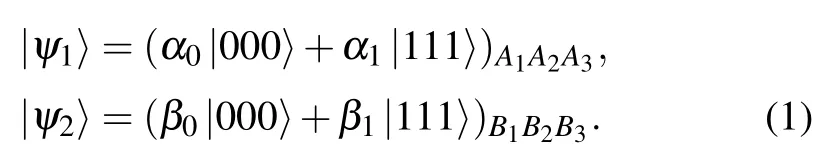
Here, the parameters α0, α1, β0, β1satisfy |α0|2+|α1|2=1 and |β0|2+|β1|2=1. To accomplish the teleportation, they need to share an eight-particle complex GHZ state|ω〉as the quantum channel in advance,which is shown in Fig.1. Alice holds the particles a1,a2,a3,b4,while Bob holds the particles b1, b2, b3, a4. |ω〉 can be described as the following tensor product of two four-particle GHZ state
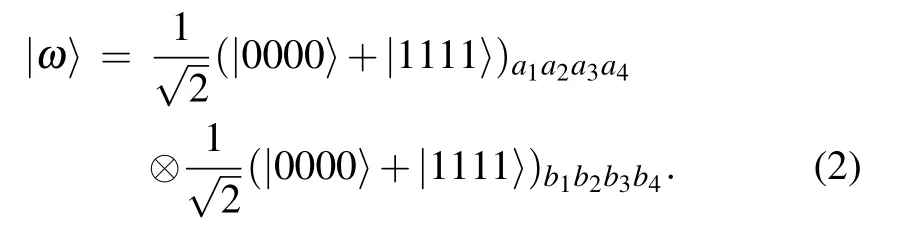
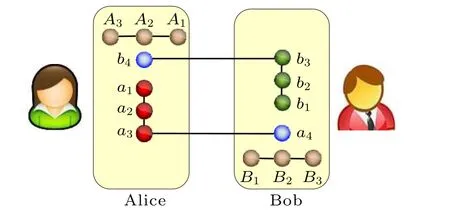
Fig.1. Quantum state preparation for bidirectional teleportation of three-particle GHZ states.
After the quantum states preparation,Alice and Bob carry out the following steps to complete the bidirectional teleportation.
Step 1They perform controlled-not(CNOT)operations respectively on particles A1and b4, B1and a4, where A1and B1are the control particles.
Step 2They perform single-qubit |Z〉-basis measurements on particles b4and a4respectively,and perform singlequbit |X〉-basis measurements on particles A2and B2respectively, then they announce the results to each other through classical channel.
Step 3They perform single-qubit |X〉-basis measurements on particles A1and B1respectively,then they announce the measurement results thriugh classical channel.
Step 4They perform single-qubit |X〉-basis measurements on particles A3and B3respectively,then they announce the measurement results through classical channel.
Step 5They perform proper three-particle unitary operations on particles a1, a2, a3and b1, b2, b3according to the measurement results in Step 2, Step 3, and Step 4, then the bidirectional teleportation is finished.
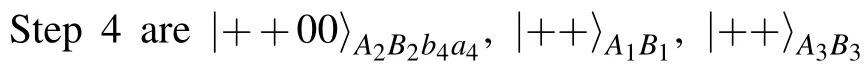
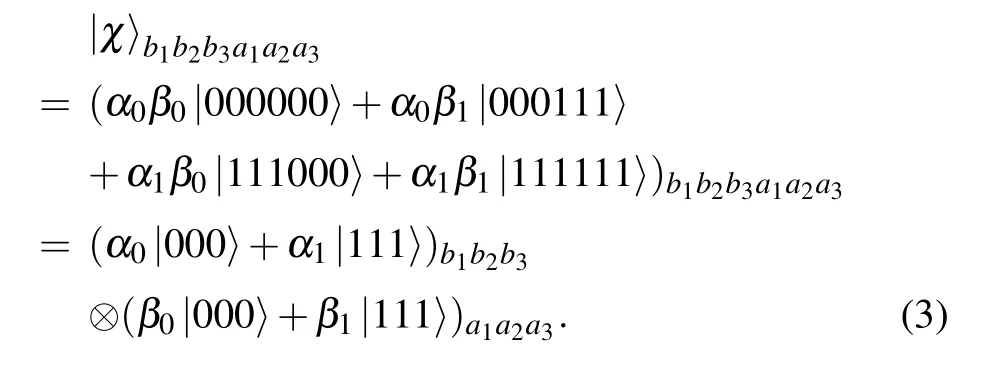
The above scheme can be extended to realizing the bidirectional teleportation of n-particle GHZ states with a 2Nparticle(N=n+1)complex GHZ channel state.
3. SES for multi-hop bidirectional teleportation of three-particle GHZ states
3.1. Basic scheme of SES
In a quantum network, there is usually no direct quantum channel between two remote users. In order to realize the bidirectional teleportation in Section 2 in a multi-hop quantum network, we propose an SES scheme that can establish the remote four-particle GHZ entanglement path. At first,we consider a scenario of three-hop SES illustrated in Fig.2. The complete process consists of the following steps.
Step 1 Entanglement state preparation and entanglement distribution

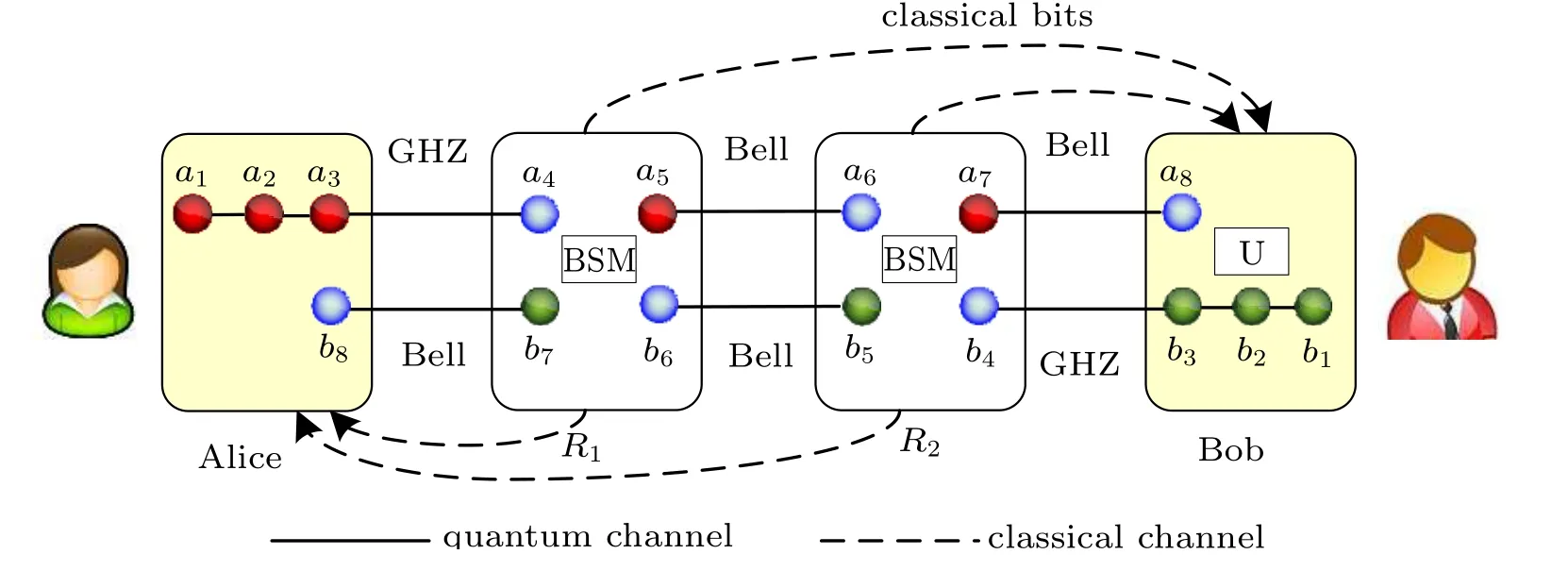
Fig.2. Three-hop simultaneous entanglement swapping of GHZ channel state.
In Fig.2, the particles a1, a2, a3, a4, a5, a6, a7, and a8constitute one channel for the bidirectional teleportation, and we call it channel A. The particles b1, b2, b3, b4, b5, b6, b7,and b8constitute the other channel, and we call it channel B.We take channel A for example. After the particles distribution,the total state of particles a1,a2,a3,a4,a5,a6,a7,and a8is expressed as
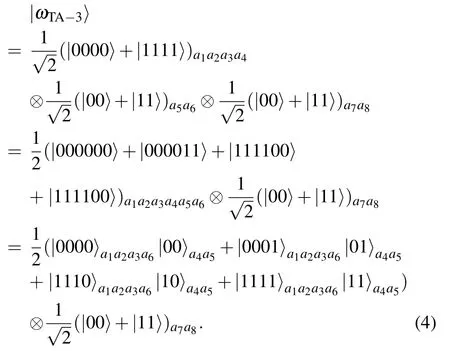


Step 2Bell state measurements and unitary operations
After the entanglement distribution, the intermediate nodes R1and R2perform Bell state measurements(BSMs)on their particles a4,a5and a6,a7simultaneously,then they obtain one of the four results |φ+〉, |φ−〉, |ϕ+〉 and |ϕ−〉 with equal probability. Nodes R1and R2encode the four measurement results into two-bit classical codes 00,01,10 or 11,then they send the two-bit codes through classical channel to Bob simultaneously. Bob carries out an appropriate unitary operation on his particle a8according to the classical codes he has received, after which a standard four-particle GHZ state|ω1〉can be established on particles a1,a2,a3,and a8between Alice and Bob. The unitary operations can be derived from Eq.(8),which are shown in Table 1. With a similar process, another standard four-particle GHZ state can be established on particles b1,b2,b3,and b8in channel B.
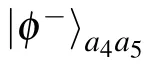
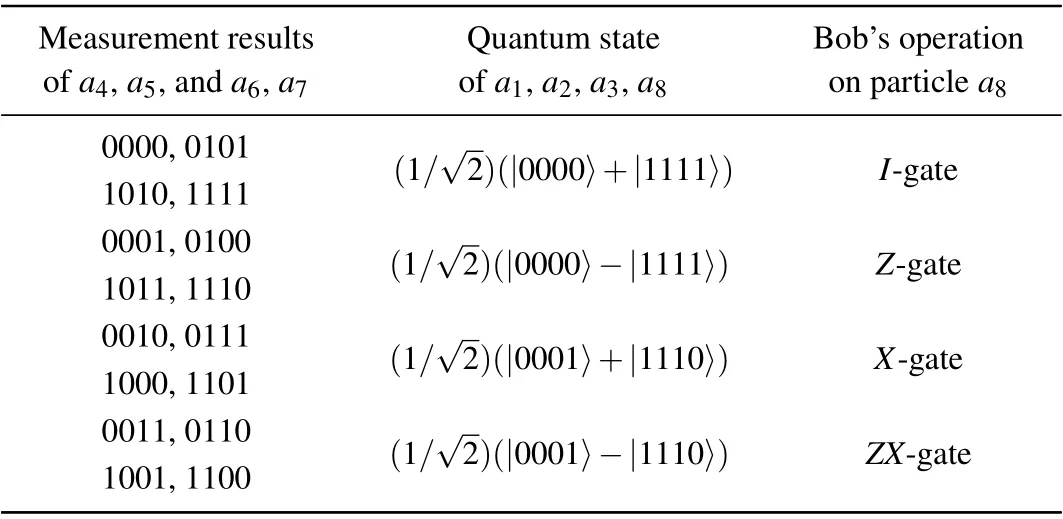
Table 1. Unitary operations of Bob in three-hop SES.
The scheme above can be easily extended to the case of N-hop multi-particle entanglement swapping. In the N-hop scenario,there are N −1 intermediate nodes numbered as R1,R2,...,RN−1between Alice and Bob. For the convenience of description,the particles held by Riin channel A are denoted as Ri1and Ri2respectively,and the two-bit result code of BSM on Ri1and Ri2is referred to as MRi1MRi2, then the unitary operations of Bob can be obtained from Table 2.

Table 2. Unitary operations of Bob in N-hop SES.
3.2. Modified unitary operations in arbitrary Bell states
In practice,the Bell state generated by each intermediate node is not always the state |φ+〉, it may be one of the four Bell states |φ+〉, |φ−〉, |ϕ+〉, |ϕ−〉. Therefore, in addition to sending the BSM results to Bob, the intermediate node also needs to send the type of the Bell state generated by itself. It can be proved that the final unitary operation that Bob adopts is related to the number of different types of Bell states generated by all intermediate nodes,while it is irrelevant to the order of the Bell states in the multi-hop quantum path. As a result,Bob needs to count the number of the four types of Bell states and calculate a modified unitary operation which is shown in Table 3.
The four-bit sequence code in Table 3 denotes the mod 2 result of the count value of the four types Bell states |φ+〉,|φ−〉,|ϕ+〉,and|ϕ−〉. Bob obtains the basic unitary operation from Table 1 or Table 2,and obtains the modified unitary operation from Table 3,then he obtains the final unitary operation by multiplying the two operations.

Table 3. Modified unitary operations.
4. The hierarchical simultaneous entanglement swapping
In the SES scheme in Section 3, each intermediate node needs to send the BSM results and the type of the Bell state to Bob through the classical channel,which will lead to considerable classical information transmission costs. In order to solve this problem, we propose a hierarchical SES(HSES)scheme in this section,and the basic process of it is shown in Fig.3.
In the HSES,the intermediate nodes on the quantum path are divided into several segments according to the scale of the network. The end node of each segment is represented in gray in Fig.3. A complete HSES process includes the following steps.
Step 1Entanglement state preparation and entanglement distribution
This step includes a similar process to the Step 1 of basic SES described in Subsection 3.1, except the fact that the end nodes must generate Bell state|φ+〉,while other intermediate nodes can generate arbitrary Bell states.
Step 2Level-one simultaneous entanglement swapping
Level-one SES refers to the entanglement swapping in each segment, and it is carried out concurrently in all segments. With a similar process to that in Subsection 3.1, each intermediate node(except the end node)in a segment performs the BSM on the two particles in each intermediate node’s hand,then transmits the measurement result and the type of the Bell state prepared in Step 1 to the end node through the classical channel. After that, the end node calculates the unitary operation according to Tables 2 and 3, and performs the unitary operation on the particle the end node holds. When the levelone SES is finished,the standard four-particle GHZ state|ω1〉will be established between the end node and the source node in the first segment,while the standard Bell state|φ+〉will be established between the adjacent end nodes in the remaining segments(e.g.the end nodes in segment i and segment i+1),which can be seen in Fig.4. Then,level-two SES will be performed.
Step 3Level-two simultaneous entanglement swapping
Level-two SES refers to the entanglement swapping between segments. The end node of each segment performs the BSM on his two particles, and sends the measurement result to Bob concurrently. In this stage, since the end node of the corresponding segment has adjusted the Bell state to|φ+〉,it is not required to transmit the Bell state type information through the classical channel. After receiving all of the measurement results, Bob calculates the unitary operation according to Table 2, and performs the unitary operation on the particle he holds, so as to establish the standard four-particle GHZ state|ω1〉with Alice.
Due to the fact that the transmission of the BSM results and the Bell state types is limited to a smaller scope in levelone swapping,and the Bell state types need not to be transmitted in level-two swapping, the classical information cost can be significantly reduced by using the HSES.
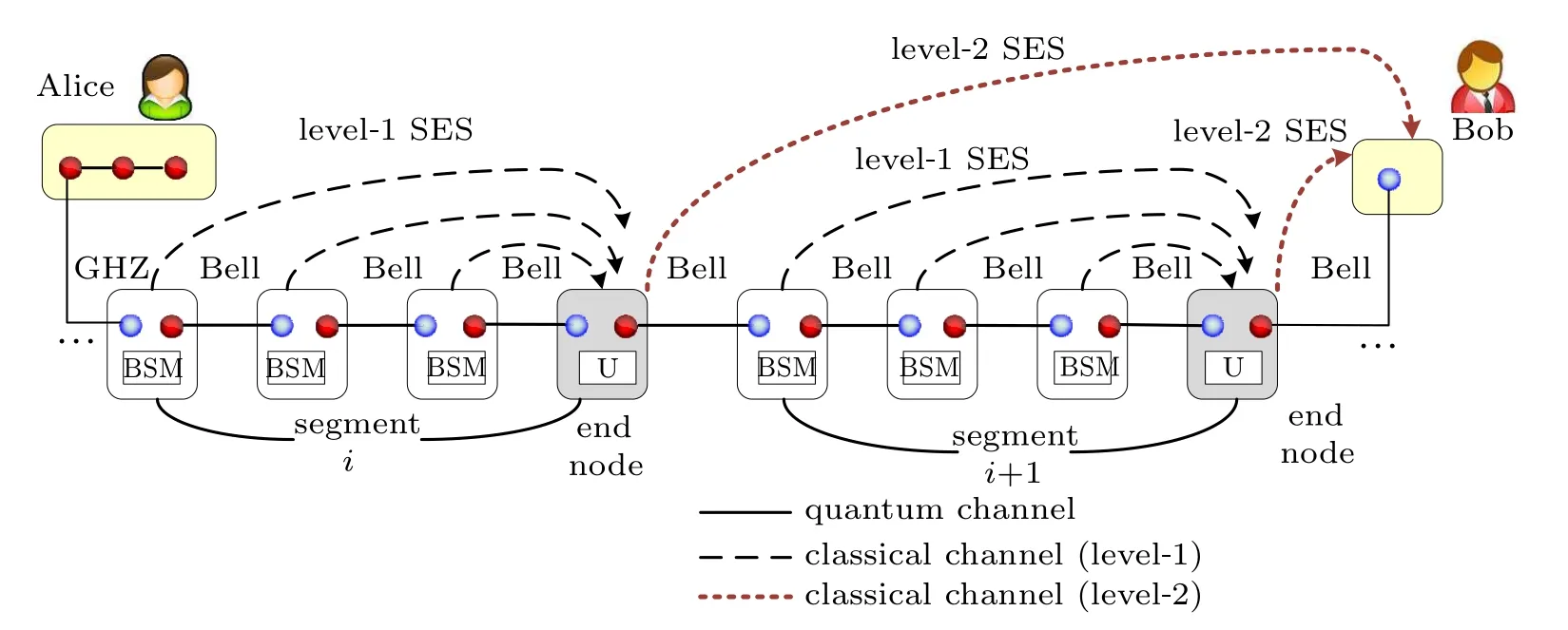
Fig.3. Hierarchical simultaneous entanglement swapping.
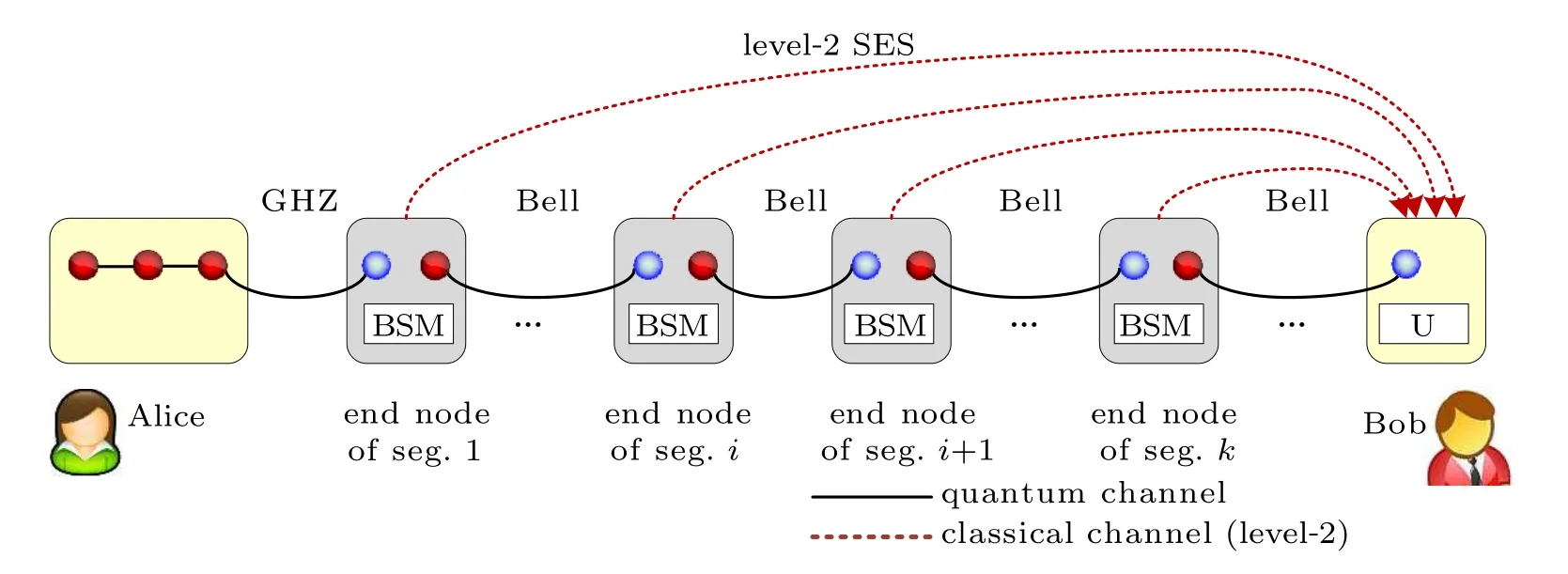
Fig.4. Level-two simultaneous entanglement swapping. Abbreviation“seg.”=segment.
5. Analysis and discussion
5.1. End-to-end time delay of entanglement swapping
Suppose that there are N hops in an entanglement swapping path between Alice and Bob,which means that the total number of the intermediate nodes is N −1.
In the SEQES, each intermediate node needs to perform the unitary operation, BSM, and classical information transmission in sequence. The total end-to-end time delay Dseqof SEQES can be calculated from the following formula
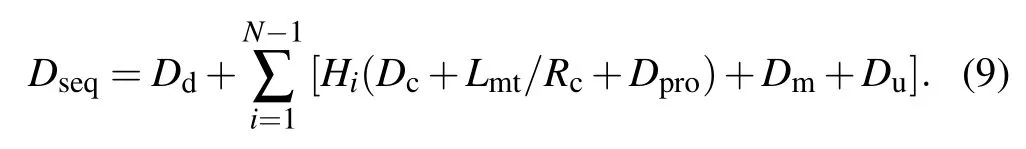
Here,Ddis the average entanglement distribution time in one quantum hop between two adjacent quantum nodes,Dcis the average information transmission delay in one classical hop,Hiis the number of the classical hops between the i-th intermediate node and the (i+1)-th intermediate node, Lmtis the total length of the classical packet which carries the information about the BSM result and Bell-state type,Rcis the transmission rate of classical information,Dprois the average processing time for a classical packet,Dmis the average time of a BSM,and Duis the average time of a unitary operation.
In the SES described in Section 3,after the entanglement distribution and the BSM, each intermediate node sends the classical information to Bob simultaneously. The delay of classical information transmission depends on the maximum delay from each intermediate node to Bob. Therefore,the total end-to-end time delay Dsof SES can be calculated from
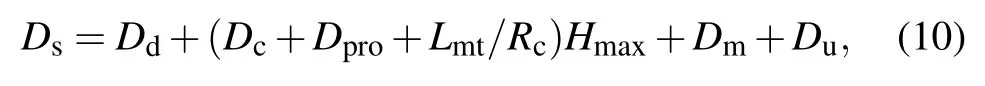
where Hmaxrepresents the maximum classical hop count between each intermediate node and Bob.
In the HSES described in Section 4, after the entanglement distribution, the delay of level-one SES depends on the maximum entanglement swapping delay of all segments, and the delay of level-two SES depends on the maximum delay from each end node to Bob. Therefore, the total end-to-end time delay Dhsof HSES can be calculated from

In Eq. (11), Hmax−srepresents the maximum classical hop count between the first intermediate node and the end node in all segments, Hmax−enrepresents the maximum classical hop count between each end node and Bob,Lmrepresents the length of the classical packet which carries the BSM result.Owing to the fact that the entanglement states between the adjacent intermediate nodes have been adjusted to standard|φ+〉in level-one SES,it is not required to transmit Bell state type information.
In the following simulation,it is assumed that the propagation rate of photon in the air is 2.996×105km,Dmis 100 ns,Duis 50 ns, Dprois 20 ns, and Rcis 100 Mbit/s. The lengths of Lmtand Lmare both taken to be 512 bits due to the fact that the classical code of BSM result and the Bell-state type must be carried in a standard data packet,then this packet should be encapsulated into MAC frame, and the length of the shortest MAC frame is 512 bits.
The end-to-end time delay of SEQES, SES, and HSES varying with the number of the intermediate nodes are shown in Fig.5. Here,the length of one quantum hop is taken to be 10 km,and the number of the intermediate nodes of one segment of HSES is taken to be 4.We can see that the time delays of the three schemes all increase with the number of the intermediate nodes increasing, and the delay of SEQES is much higher than that of SES and HSES. This is because an intermediate node must perform the required processes one after another in SEQES,yet in SES and HSES,intermediate nodes can perform these processes simultaneously. Meanwhile, the time delay of HSES is slightly higher than that of SES.
Suppose that the distance from Alice to Bob is given,the end-to-end delay of SEQES,SES,and HSES are given in Fig.6. when the per-hop length between two adjacent intermediate nodes is separately 5 km, 10 km, and 20 km. The number of the intermediate nodes in one segment of HSES is taken to be 4 when the per-hop length is separately 10 km and 20 km, and it is taken to be 8 when the per-hop length is 5 km. It can be seen that the delay of SEQES is still higher than that of HSES,while the delay of HSES is slightly higher than that of SES.When the per-hop length is 20 km,SEQES,SES,and HSES all obtain the lowest time delays,and they obtain the highest time delays when the per-hop length is 5 km.Obviously,a shorter per-hop length means a larger number of intermediate nodes when the distance from Alice to Bob is given. In other words, it will lead the end-to-end delay to increase when too many intermediate nodes are placed between Alice and Bob. However, when the number of the intermediate nodes decreases,the length between adjacent nodes will increase,which brings about the considerable decoherence and noise in quantum channel. As a result,it is very important to determine the per-hop length appropriately.
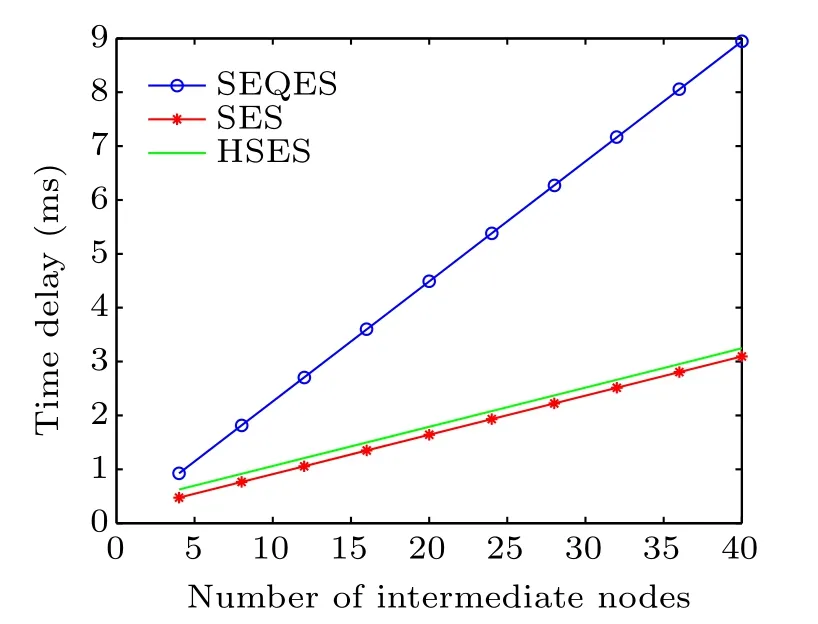
Fig.5. Time delay versus number of intermediate nodes for SEQES,SES,and HSES.

Fig.6. Time delay versus length of nulti-hop path for SEQES and HSES in the case of different per-hop lengths.
5.2. Classical information cost of entanglement swapping
In the SEQES,each intermediate node needs to send the classical information about the BSM results and the type of the Bell state to the next intermediate node. The overall classical information cost of SEQES is
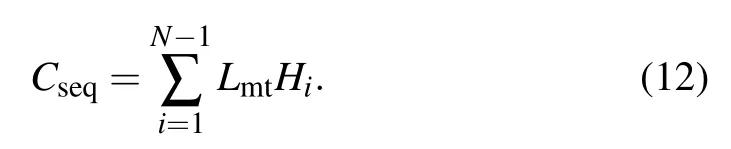
In the SES described in Section 3,each intermediate node needs to send classical information to Bob,so the overall classical information cost can be calculated from

In the HSES described in Section 4, the overall classical information cost is
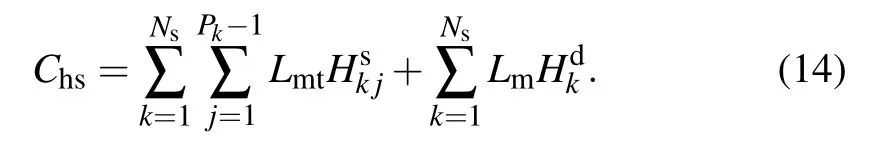
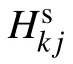

In the following simulation,we use the packet as the unit of the classical cost due to the fact that the classical information should be carried in a data packet which is encapsulated in Mac frame.
The classical costs of SEQES, SES, and HSES varying with the increase of the number of intermediate nodes are shown in Fig.7. Here,we assume that the classical hop count between two adjacent intermediate nodes is 1, and we take 4 intermediate nodes in one segment in HSES.It can be seen that the classical cost of SES is the highest in the three schemes,while the classical cost of HSES is much lower than that of SES,and the classical cost of SEQES is the lowest.
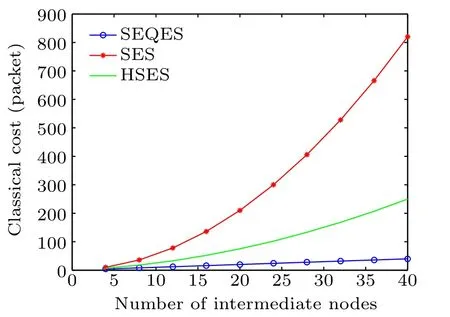
Fig.7. Classical costs versus number of intermediate nodes for SEQES,SES,and HSES.
Suppose that the total number of the intermediate nodes between Alice and Bob is given, figure 8 shows the classical costs of HSES when the numbers of intermediate nodes are 1,4,8,and 16 in one segment. It can be seen that when there is 1 node in a segment,which is equal to the scenario of SES,the classical cost is the highest; and the cost is the lowest when there are 8 nodes in a segment,while the cost in the case of 4 nodes and 16 nodes are a bit higher. Therefore,a larger node number in a segment does not always bring lower cost because it leads to a higher cost of level-one SES. Consequently, it is very important to give an appropriate segmentation method,thereby obtaining an optimal classical cost.
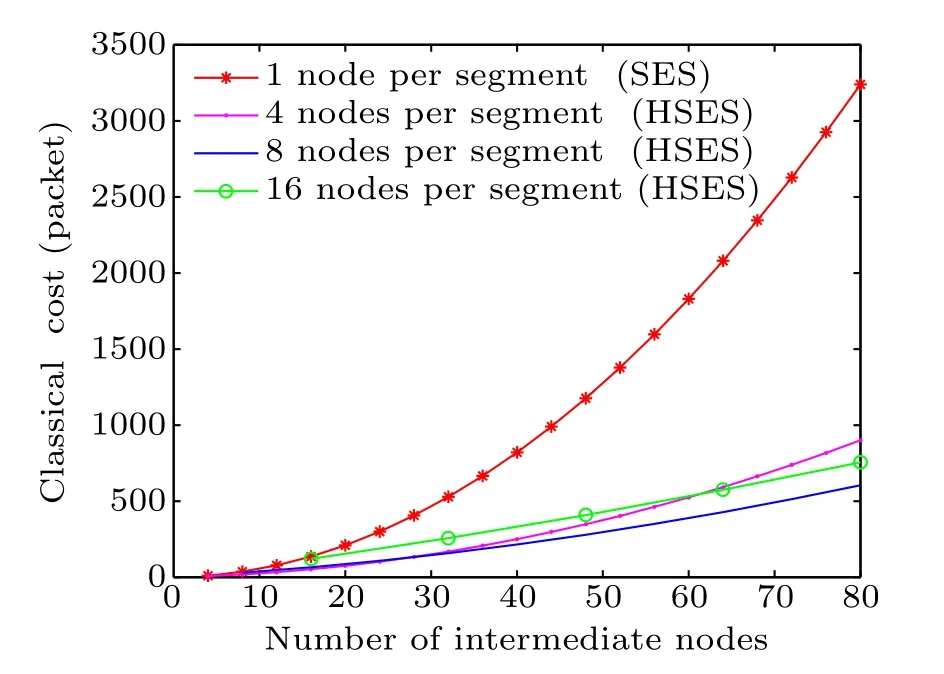
Fig.8. Classical costs versus number of intermediate nodes for HSES with different numbers of nodes in one segment.
Assume that the total number of the intermediate nodes is given in HSES,figure 9 shows the comparison among the classical costs when the classical hop counts between two adjacent intermediate nodes are different.The number of the intermediate nodes in one segment is taken to be 4. From Fig.9. we can see that the classical cost is the highest when the classical hop count is 3,while it is the lowest when the classical hop count is 1. Due to the fact that each classical node in one classical hop must store and forward the classical packets,the classical cost rises with the increase of the classical hop count.

Fig.9. Classical costs versus number of intermediate nodes for HSES with different classical hops between adjacent quantum intermediate nodes.
5.3. Discussion on challenge of Bell-state measurement
A significant challenge in multi-hop quantum entanglement swapping is the need of performing complete BSM,which also plays a critical role in other quantum information tasks,such as quantum teleportation and quantum dense coding. However,traditional BSM schemes with linear optics can only distinguish two of the four Bell states unambiguously,thus the success probability is no more than 50%.[40-42]
Although the complete BSM schemes with nonlinear optical elements have been presented, such as the cross-Kerr nonlinearity and the quantum-dot system,[43-45]they are still hard to put into practical application. In the past few years,researchers have been working on achieving a complete BSM with linear optics, and several improved schemes have been proposed, such as the use of auxiliary particles,[46,47]compression operation,[48]and ancillary degree of freedom(DOF).[49-52]Grice proposed a complete BSM by using the linear optical elements with the addition of ancillary entangled photons,[46]showing that the addition of 2N−2 ancillary photons yields a success rate of 1 −1/2N. Zaidi and van Loock presented a dual-rail unambiguous BSM scheme by using single-mode squeezers and beam splitters with a success probability of 64.3%.[47]Kwait and Weinfurter first proposed a scheme to perform the complete BSM with linear optics by using entanglement in polarization DOF and ancillary DOF.[48]After that,a series of complete BSM schemes was put forward by using the hyperentangled states,such as hyperentanglement in polarization-momentum,[49]polarization-frequency,[50]and polarization-time mode.[51,52]In these schemes,the quantum message is usually carried by the polarization DOF,while the ancillary DOFs are used to expand the measurement space.
Owing to the above progresses, the practical BSM technology has been greatly developed, while how to distinguish Bell states unambiguously and efficiently in quantum information fields is still a very crucial research topic,and this will also be an important aspect of our future work.
6. Conclusions
In this work, we present a multi-particle HSES scheme for the bidirectional teleportation of three-particle GHZ states,in which the intermediate nodes on the quantum path are divided into several segments, and the whole entanglement swapping includes level-one SES and level-two SES. Owing to the fact that the classical information transmission is limited to a smaller scope in level-one SES, and only the intermediate nodes need to transmit classical information to Bob in level-two SES, the classical information cost can be significantly reduced. Compared with the existing SEQES and SES schemes, the HSES has the advantages to obtain the optimal performance tradeoff between the end-to-end delay and the classical information cost.
The HSES scheme in this paper can be easily extended for other quantum communication tasks. Generally, a large scale quantum network is divided into quantum access network(QAN)and quantum core network(QCN).In the QAN,different types of entanglements can be distributed between the user node and the network edge node according to the requirements of quantum communication tasks,such as W state,GHZ state, cluster state, etc. In the QCN, the intermediate nodes only need to prepare and distribute Bell states. Using the HSES scheme, the multi-hop entanglement between remote users can be established with low delay and low classical information cost. Such a scheme is of positive value for improving the quality of large scale quantum networks and promoting the development of practical quantum communication,which will have a potential application prospect in constructing the future quantum land networks and quantum satellite networks.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Nonlocal advantage of quantum coherence in a dephasing channel with memory∗
- New DDSCR structure with high holding voltage for robust ESD applications∗
- Nonlinear photoncurrent in transition metal dichalcogenide with warping term under illuminating of light∗
- Modeling and analysis of car-following behavior considering backward-looking effect∗
- DFT study of solvation of Li+/Na+in fluoroethylene carbonate/vinylene carbonate/ethylene sulfite solvents for lithium/sodium-based battery∗
- Multi-layer structures including zigzag sculptured thin films for corrosion protection of AISI 304 stainless steel∗
