Impact of counter-rotating-wave term on quantum heat transfer and phonon statistics in nonequilibrium qubit-phonon hybrid system∗

Chen Wang(王晨), Lu-Qin Wang(王鲁钦), and Jie Ren(任捷),‡

1Department of Physics,Zhejiang Normal University,Jinhua 321004,China

2Center for Phononics and Thermal Energy Science,China-EU Joint Center for Nanophononics,Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology,School of Physics Science and Engineering,Tongji University,Shanghai 200092,China

Keywords: quantum transport, open systems, nonequilibrium and irreversible thermodynamics, phonons or vibrational states in low-dimensional structures and nanoscale materials

1. Introduction

Understanding and managing nonequilibrium energy transfer at nanoscale is a long-standing problem, which has attracted great attention with scientific interest and practical importance.[1-3]Theoretically,the microscopic description of the system-bath coupling in open small quantum systems is crucial to model the quantum heat flow, as the systembath coupling describes the dissipation of the small quantum system to the external environment.[4,5]In particular,the strong couplings between the small quantum system and surrounding baths significantly contribute to the transient and steady state heat transport properties, including energy exchange dynamics,[6-11]quantum thermodynamics and thermal machines,[12-18]and quantum heat transfer.[19-27]

One of the most representative paradigms of the systembath dissipation is the spin-boson(qubit-bath)coupling[28]

where

Here,we propose that at strong qubit-phonon hybridization inside the central system, CRWTs of the (even weak)qubit-bath dissipation may novelly contribute to the transport behaviors of hybrid quantum systems. The main points of this work have three manifolds: (i)Based on the quantum master equation encoded with extended coherent phonon states, we obtain microscopic pictures of heat exchange processes,which are separately contributed by RWTs and CRWTs. (ii) By including full counting statistics(FCS)with weak system-bath interactions,the heat current and fluctuations are strongly suppressed at large temperature bias with the qubit-bath dissipation considering only RWTs,whereas the heat current fluctuations are greatly enhanced by considering CRWTs in addition.This clearly demonstrates the novel role of CRWTs on steady state heat transfer. (iii) The steady state phonon number and two-phonon correlation function with RWTs are nearly insensitive to the strong qubit-phonon hybridization,whereas they are optimally cooled down via the cooperative transition path contributed by both RWTs and CRWTs.

This paper is organized as follows. We describe the nonequilibrium qubit-phonon hybrid model in Subsection 2.1,derive the quantum master equation in Subsection 2.2,and obtain the expression of heat current fluctuations by including full counting statistics in Subsection 2.3. In Section 3, we investigate the steady state heat transfer, which is characterized by heat current,noise power,and skewness. In Section 4,we analyze the steady state phonon number and two-phonon correlation function of phonon statistics. Finally, we give a conclusion in Section 5.

2. Model and method

2.1. Qubit-phonon hybrid system

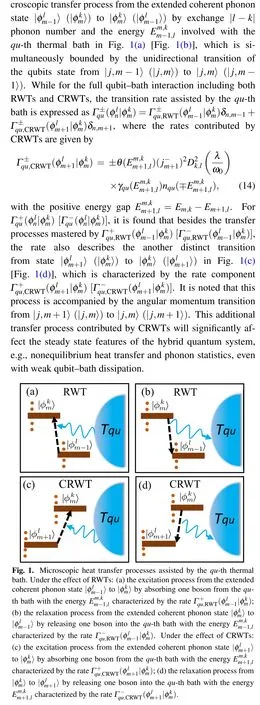
Specifically,the hybrid system is expressed as

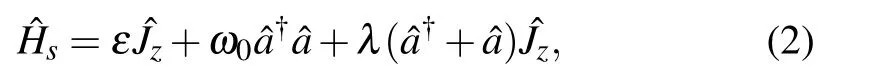
It should be noted that though the nonequilibrium qubitphonon hybrid system is theoretically investigated in the present paper, it has experimental correspondences. Specifically,the hybrid quantum system can be specified by the system composed by the nanomechanical resonator and single quantum dot,[70]where the resonator and quantum dot interact with the bosonic thermal and magnon reservoir,[71,72]respectively. The CRWTs in Eq.(4)can be realized by the interfacial interaction with non-spin-conservation.[73]Moreover,it could also be realized by the circuit-QED setup,[48]where one josephson junction could be longitudinally coupled to a LC resonator.[74-77]While for the spin-boson model, under the reaction coordinate mapping approach,it can be mapped to another type of qubit-phonon hybrid model.[6,10,78-82]From the aspect of inverse design,the analysis of quantum heat transfer in nonequilibrium qubit-phonon hybrid systems could fertilize theoretical interact and practical application of the spin-boson model.

2.2. Quantum master equation

We plot the heat current at resonance in Fig.2(a) as one typical instance to analyze the effect of the finite qubit number N on steady state behaviors. It is found that in the small qubit number limit(e.g.,N=1,2)the heat current with the full interaction between the qubits and the qu-th bath is dramatically enhanced over a wide qubit-phonon coupling regime,compared to the counterpart affected by only RWTs. This demonstrates the nontrivial contribution from CRWTs. However,as the qubit number becomes large(e.g.,N=8),the currents from two different types of qubit-bath interactions(i.e.,RWTs and full interaction)become nearly identical,which implies that RWTs dominate the behavior of the heat current.Moreover, it needs to note that we set the truncation number of phonons Nphto 30, which is sufficient to make the steady state quantities converge based on numerical calculations,e.g.,the heat current with full qubit-bath interaction in Fig.2(b).Therefore, we select N =1 in the following to manifest the novel role of CRWTs.

Fig.2.Steady state heat current out of the ph-th thermal bath as a function of the qubit-phonon hybridization strength(a)under the effects of only RWTs and full qubit-bath interaction(including both RWTs and CRWTs)with various qubit numbers, and (b) by tuning the truncation number of phonons Nph with full qubit-bath interaction and N =8. The other system parameters are given by ε =1, ω0 =1, αph =αqu =0.005, Tph =1.5, Tqu =0.5,and ωc=10.

3. Quantum heat transfer

In this section, we investigate heat current, noise power,and skewness at steady state, which are the representative characteristics of quantum heat transfer.In one previous work,we mainly investigated the steady state heat current and the effect of negative differential thermal conductance (NDTC)with weak qubit-phonon hybridization,[49]where the role of CRWTs was not explicitly explored. Here, we focus on the comparison of heat current fluctuations owning RWTs to the counterpart with full qubit-bath interaction, i.e., including both RWTs and CRWTs, at strong qubit-phonon hybridization.

We first study the steady state heat current out of the phth thermal bath(−J)in Fig.3. Under the influence of RWTs,figure 3(a) exhibits a globally optimal peak at finite temperature bias (ΔT≈0.5) and strong qubit-phonon hybridization strength (λ≈2). This clearly demonstrates that the effect of NDTC can also be observed with strong qubit-phonon hybridization with only RWTs. In sharp contrast, by including both RWTs and CRWTs we find that the heat current shows monontonic enhancement by increasing the temperature bias in the strong hybridization regime, as shown in Fig.3(b).Moreover,we unravel such distinction from the aspect of heat current fluctuations. Specifically, for the noise power and skewness with only RWTs in Figs.3(c)and 3(e),they are significantly suppressed at large temperature bias (e.g., Tph≈2 and Tqu≈0), Whereas the counterparts show dramatic enhancement by including CRWTs in Figs.3(d)and 3(f).Hence,we conclude that CRWTs nontrivially enhance the steady state heat transfer with strong qubit-phonon hybridization,particularly in large temperature bias regime.

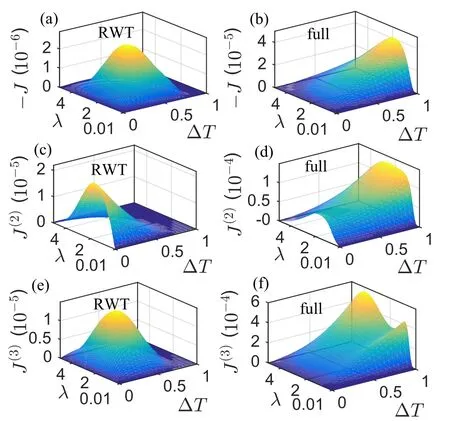
Fig.3. (a) and (b) Steady state heat current (−J), (c) and (d) noise power[J(2)], (e) and (f) skewness [J(3)] by modulating both the temperature bias ΔT and qubit-phonon hybridization strength λ under the effects of RWTs and CRWTs, with Tph =T0+ΔT, Tqu =T0 −ΔT, and T0 =1. The other system parameters are given by ε =1,ω0 =1,N =1,αph =αqu =0.005,and ωc=10.

5. Conclusion

To summarize, we have studied steady state statistics of the nonequilibrium qubit-phonon hybrid system by applying quantum master equation under the extended coherent phonon states, where the phonon-bath and qubit-bath dissipations are weak. At steady state, the natural disappearance of offdiagonal terms of the reduced hybrid system density matrix simplifies the generalized master equation to the dressed mater equation. For steady state heat transfer, we have adopted the full counting statistics to compare the heat current and current fluctuations under the effects of only RWTs and full qubitbath interaction including both RWTs and CRWTs.

We first investigated the heat current at strong qubitphonon hybridization. It has been found that the current always shows the behavior of NDTC under the effect of RWTs.In particular at the large temperature bias limit, the unidirectional transition from the extended coherent phonon states in spin-up branch to the counterparts in spin-down branch prevents the hybrid system from establishing a thermodynamic cycle,as shown in Fig.1(b).Such suppression mechanism persists also for current fluctuations,e.g.,noise power and skewness. On the contrary,the heat current and current fluctuations contributed by both RWTs and CRWTs exhibit monotonic increase by increasing the temperature bias.The novel transition controlled by CRWTs in Fig.1(d)restores the thermodynamic cycle.

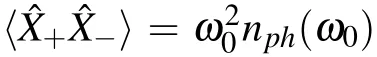
Appendix A:Generalized quantum master equation

By individually perturbing the phonon-bath and qubitbath interactions in Eqs.(3)and(4),we obtain the generalized master equation under the Born-Markov approximation as