球形颗粒干湿循环过程中的液桥作用规律
2021-03-19杨东升冯文凯白慧林易小宇顿佳伟曾唯恐
杨东升,冯文凯,白慧林,易小宇,顿佳伟,曾唯恐
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室, 四川 成都 610059)
含水率是影响土体性质变化的一个重要因素。土体中随含水率变化而变化的指标有很多,如随着土体含水率的升高,基质吸力开始单调递减,毛细黏聚力表现为先增后减;前者为非饱和土的一个重要强度指标,而后者可使砂土产生假黏聚现象。
由Young-Laplace方程与土水特征曲线的滞回效应可以得知,即使在含水率相同的情况下,非饱和土干湿循环过程中的吸湿、脱湿过程对应的孔隙水“气-液”界面的曲率存在很大差异。因此相应的液桥作用规律也是不同的。
由于液桥作用力影响因素的复杂性,如电湿润效应[1]、咖啡环效应[2]等,大多数学者在研究此类问题时以无黏性颗粒材料为研究对象,且发现对于无黏性土颗粒间的液桥形态随含水率的变化表现出很明显的阶段性:“悬挂状”阶段和“索状”阶段,见图1。
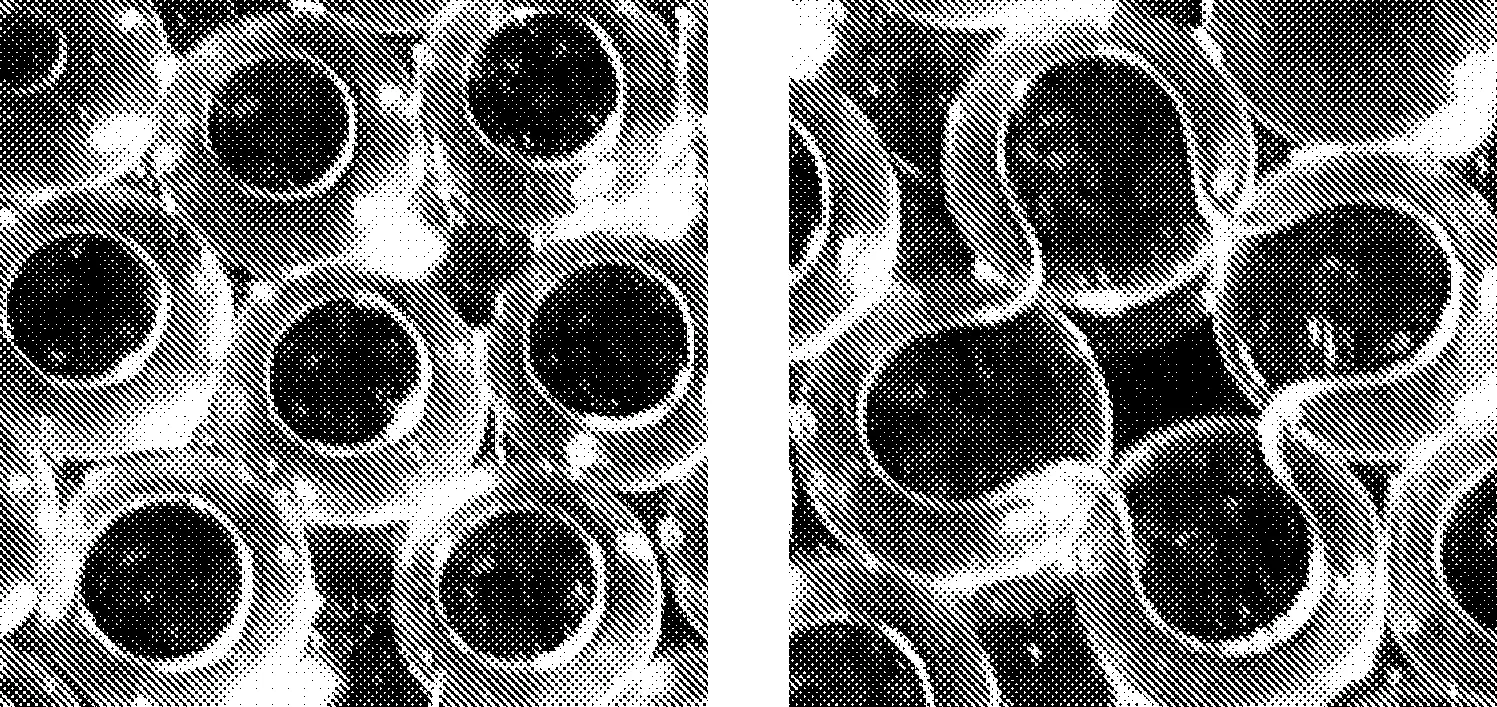
图1 “悬挂状阶段”(左)与“索状阶段”(右)
在颗粒含水率较少时,液桥相互孤立,此时一般只连接两个颗粒。此时的液桥形态称为“悬挂状”阶段。这一状态对应双颗粒液桥模型。现有模型中的颗粒形状多为“球形”及“片状”,包括等径/不等径“球形”颗粒模型[3-6]、“球形-片状”颗粒模型[7-9]、平行/不平行“片状”颗粒模型[10-12]等。
当含水率继续升高,液桥体积逐渐增大,相邻液桥相互接触、合并达到“索状”阶段,合并后的液桥可同时连接两个甚至更多颗粒,至此,双颗粒液桥模型不再适用,继而有学者提出三颗粒接触模型[13-14]等。
以上液桥模型都是基于静态或准静态过程,并且在大多数情况下不考虑液桥的浮力[15]。当液桥形态相对简单,如对于“两球形颗粒”构成的液桥模型,若液桥的特征尺度(水约为2.72 mm)小于毛细长度时通常采用圆环假设[8,12-13],此时往往通过理论公式直接对液桥力进行计算。当“气-液”界面形态较为复杂,如液桥处于“索状阶段”,或是需考虑重力对“气-液”界面的形态的影响时,则常通过建立的热力学模型求其数值解。汤连生等[16-17]认为对非饱和土湿吸力及有效应力进行计算时,应按不同的含水率阶段分别进行计算。
除了从以上“细-微观”层面对不同液桥模型进行探究,也有学者使用水土作用原理解释一些土体的宏观现象[18-22]。唐朝生等[23-24]从水土作用原理出发对土体干裂规律进行分析,并认为从宏观上分析,基质吸力和抗拉强度是控制龟裂发育的两个关键指标。倪可等[25]从表面张力的角度分析了油污土干裂隙形成发育机理。但他们都未对干湿循环全过程中液桥作用力的特征进行对比研究。
为了探究含水率变化对液桥力及颗粒运移的影响,本研究将使用等粒径(2 mm)、表面光滑的透明玻璃珠颗粒材料,研究吸湿至饱和状态以及因水分自然蒸发而脱湿至孔隙水含量为零的过程中,“液桥”对颗粒的细观作用规律。由于孔隙流体入渗过程中,液桥对颗粒的湿润作用往往不可视作准静态过程,因此试验将使用高速相机对单颗、双颗、三颗玻璃珠,以及玻璃珠群湿润过程中的运动特征进行捕捉观测和规律分析。
1 试验设计
1.1 试验目的
限于现有的科学技术手段,无法对实际土体中吸湿、脱湿过程的液体表面张力与土体细观结构的耦合效应进行直观有效地观测。因此本文设计了细观二维物理模型试验对此类问题进行探究。通过高速摄像机记录玻璃珠在吸湿、脱湿过程中的等时间间隔运动轨迹,来反演吸湿及脱湿过程中液桥对玻璃珠的作用力的变化规律。
1.2 试验装置
为有效地对液桥力进行观测,需合理地简化试验边界条件。在细观层面,若从土体内取任意土颗粒为隔离体进行受力分析,则土体密实度、黏土类矿物的晶间膨胀力、重力等带来的影响都可以简化为颗粒之间的相互作用力,不仅对本文的研究重点——“液桥力”无明显影响,还会大大减少试验中可自由移动的颗粒数量,影响试验观测结果。因此本试验在设置边界条件时,仅控制颗粒的排列方式,并尽可能减少玻璃珠与载玻片间的摩擦力、相互作用力等。
试验装置具体如图2所示。整套试验装置由三部分组成:供水部分、试验样本及图像采集装置。供水装置为带有注射针头的医用吊瓶;对吊瓶的供水流量进行标定后,以恒定速率往颗粒材料一侧进行供水直至试验结束。经检验,试验中设置的流量相较于样本间孔隙体积较小,其产生的渗流力不可以忽略不计。
所有试验样本都由表面光滑的 上下载玻片及玻片中间一定数量的光滑等径玻璃珠组成,三者之间的孔隙构成了颗粒材料吸湿及脱湿的水力通道。
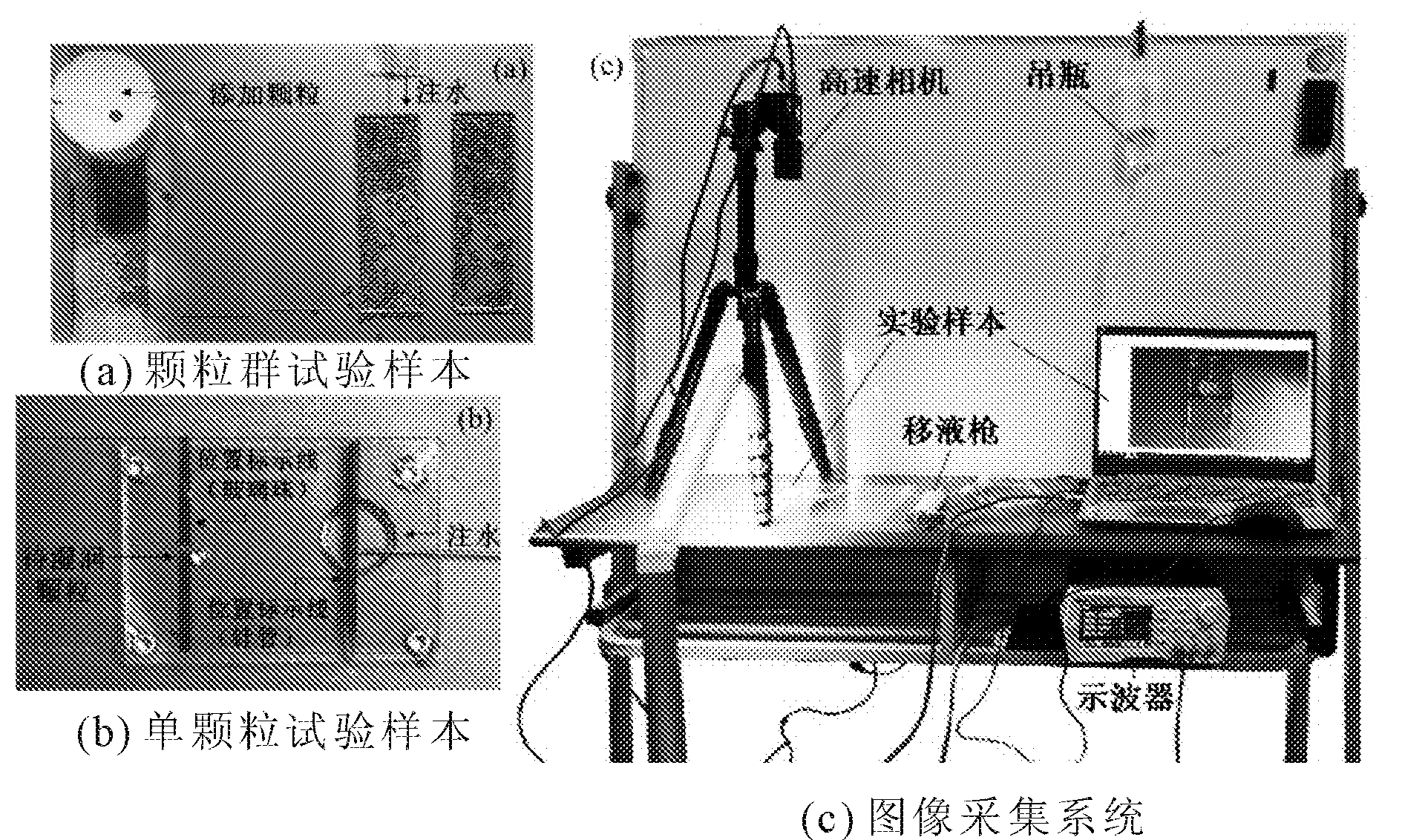
图2 试验装置及试验样本
1.3 试验方案
本试验的研究重点为颗粒群试验,通过试验过程中呈现的颗粒群的颗粒排列规律探究液桥作用力与颗粒结构的耦合关系,通过单颗粒试验可从单个颗粒受力的角度对颗粒群试验的试验结果进行分析。
详细试验方案如表1所示,首字母为“L”的试验序号代表单粒玻璃珠的试验组,首字母为“M”的试验序号为颗粒群试验组。是为了验证试验结论的可重复性,设置了若干组重复试验。以单粒玻璃珠试验为例,五组重复试验的编号依此为Ai—Ei,“i”为对应实验组的数字序列(L1对应的重复试验编号为A1—E1)。对颗粒群试验单独设计了干湿循环过程,一次吸湿-脱湿记为一个循环。
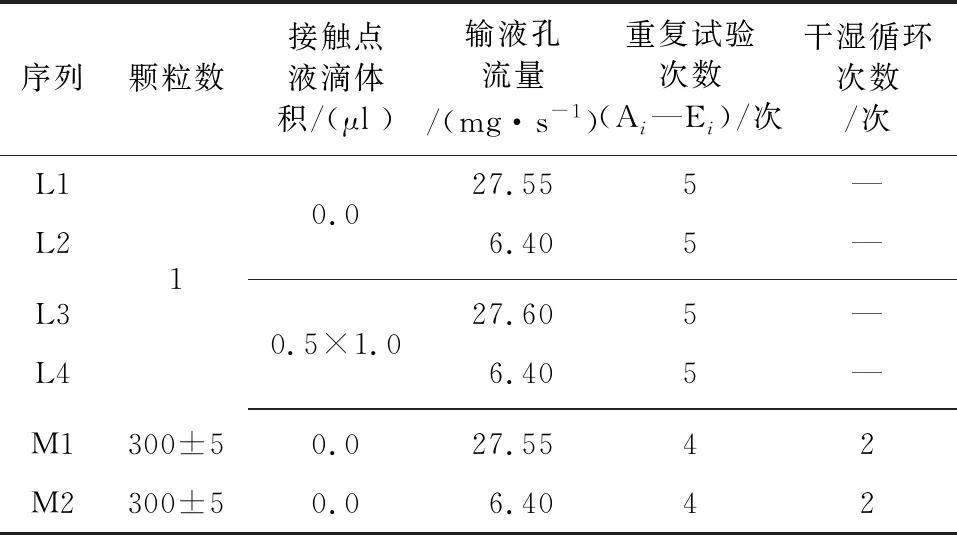
表1 试验方案
2 试验结果及分析
2.1 颗粒群
颗粒群试验吸湿过程结束判定标准为:载玻片间所有颗粒完全被湿润;脱湿过程的结束判定标准为:玻璃珠与上载玻片间的接触点间水分完全蒸发。
由于颗粒群试验过程中的输液流量对试验结果无显著影响,且重复试验的试验结论具有相似性,因而选取了两个具有代表性的试验结果(A、B)进行展示。如图3所示。

图3 可观察到颗粒集群
吸湿阶段。第一次吸湿与第二次吸湿的吸湿路径有很大区别。第一次吸湿过程湿润锋面呈较为规则的圆弧形,见图4(a(2))、图4(b(2));第二次吸湿过程很难看见明显的湿润锋面(见图4a(7))或者湿润锋面不明显(见图4b(7))。这是由于第一次脱湿结束后玻璃珠与下载玻片间还存在少量液滴,而液体会优先湿润已湿润区域[26],因此当第一次干湿循环过后试验样本中铺有颗粒的区域成为了吸湿的“优势通道”。通过观察发现,吸湿过程中,可分为三个阶段:(1) 玻璃珠初次接触液桥后将受到瞬时的作用力被拖往液桥内部;(2) 玻璃珠位移基本稳定后以液桥相对玻璃珠的湿润行为为主;(3) 玻璃珠达到某一临界的湿润面积后,颗粒群边缘颗粒可随液桥一并推移。
脱湿阶段。在试验过程中颗粒材料的脱湿过程,有如下显著顺序:(1) 饱和的颗粒材料从边缘开始逐渐脱水;(2) 沿大孔隙退缩为以各颗粒集群为单位的“索状阶段”;(3) 若无次级孔隙,则在集群“索状阶段”的基础上退化为“悬挂状阶段”;(4) 水分蒸发殆尽。以上所述的集群指的是,紧挨着的水分分配结果一致的颗粒群体。
图3所示样本为图4(a)矩形虚线范围处的局部特写,由图3(a)可明显看出颗粒在小范围内的聚集现象,而图3(b) 将图4(a)中第一次脱湿的过程更加全面地展开,图3(a)、图3(b)共同展示出了“集群”对颗粒群脱湿阶段性的影响。
对比吸湿与脱湿过程,发现了以下规律:
(1) 相对吸湿过程,脱湿试验对颗粒结构的扰动要大得多,且主要发生在第一次脱湿过程。图4第一次脱湿结束与第二次脱湿结束的颗粒群结构差异较小。这一现象与干湿循环土样的性质(强度、变形)有关,主要发生在第一次干湿循环之后[27-30]。说明干湿循环过程中,液桥力在土体结构劣化中起到了重要作用。
(2) 颗粒结构的改变几乎只发生在液桥的“索状阶段”。图4第一次脱湿过程中“5”到“6”基本未发生颗粒结构改变。这是因为“索状阶段”的液桥作用力比“悬挂状阶段”的液桥作用力高的多[13-14],并且“索状阶段”位于“悬挂状阶段”之前。
(3) 虽然颗粒结构的扰动主要发生在第一次干湿循环,但从本试验来看后续的循环效应同样不容忽视。如图4(a)中矩形范围所示,直至第二次干湿循环结束,颗粒群中不同集群间的间隙才开始变得显著。

图4 颗粒群试验
2.2 单颗粒
如2.1节所述,湿润过程中液桥对玻璃珠的作用可分为三个过程。由于(2)过程玻璃珠几乎无位移,(3)过程位移量过于微小无法捕捉,因此单颗粒试验仅针对(1)过程开展。
为了直观地展示单粒玻璃珠在与“液桥”接触后运动过程,将试验中拍摄的等时间间隔中玻璃珠轮廓线提取出来。由于每个实验过程中玻璃珠的位移参考系未发生改变,因此可以将同一次试验提取的玻璃珠轮廓线展示在同一坐标系中,此时轮廓线圆心连线即为一次实验中玻璃珠的运动轨迹(见图5)。照片的提取从实验开始至玻璃珠朝液桥液相方向的位移量为零时结束。
为便于比较分析,将玻璃珠圆心轨迹置于坐标系中进行比较,坐标原点为玻璃珠位移的起点,y轴方向以玻璃珠朝液桥液运动的方向为正。由于高速摄像机是以等时间间隔进行拍摄,即图6相邻节点间的时间间隔相等。因此图6亦可较好地反应玻璃珠的运动速度变化规律。图6中图例标示与表1对应重复试验序号对应,详见1.3节。
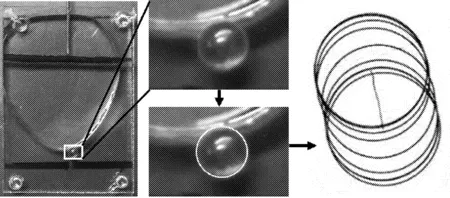
图5 试验数据提取(以表1,L4的结果为例)
对比同一实验序列重复试验可以发现。实验组L3、L4重复试验的玻璃珠运动轨迹彼此差异较大,这是由于存在接触角滞后现象,等体积液滴在载玻片表面的铺展面积并不是定值;并且试验组L3、L4都出现了y坐标为负的位移轨迹,这与玻璃珠接触点间的液滴与载玻片间液桥融合后,液桥内部压力开始重新分配有关。
从轨迹的长度看,试验组L3、L4的单条轨迹的纵向长度分别在70 μm~400 μm、500 μm~1 100 μm之间波动,二者差异较大;而试验组L1、L2的单条轨迹的纵向长度都在70 μm~400 μm之间波动。这是由于玻璃珠与载玻片接触点间的液滴的液桥力会阻碍玻璃珠移动。表明液桥流速对接触点间存在液滴的玻璃珠的位移总量影响相对更大。
对比L1、L2、L3、L4四个试验序列的试验条件可以发现。对于接触点初始无液滴的试验(L1、L2),输液流量对玻璃珠运动轨迹长度的影响不大;而对于接触点间存在液滴的试验(L3、L4),输液流量对玻璃珠运动轨迹长度影响较大。
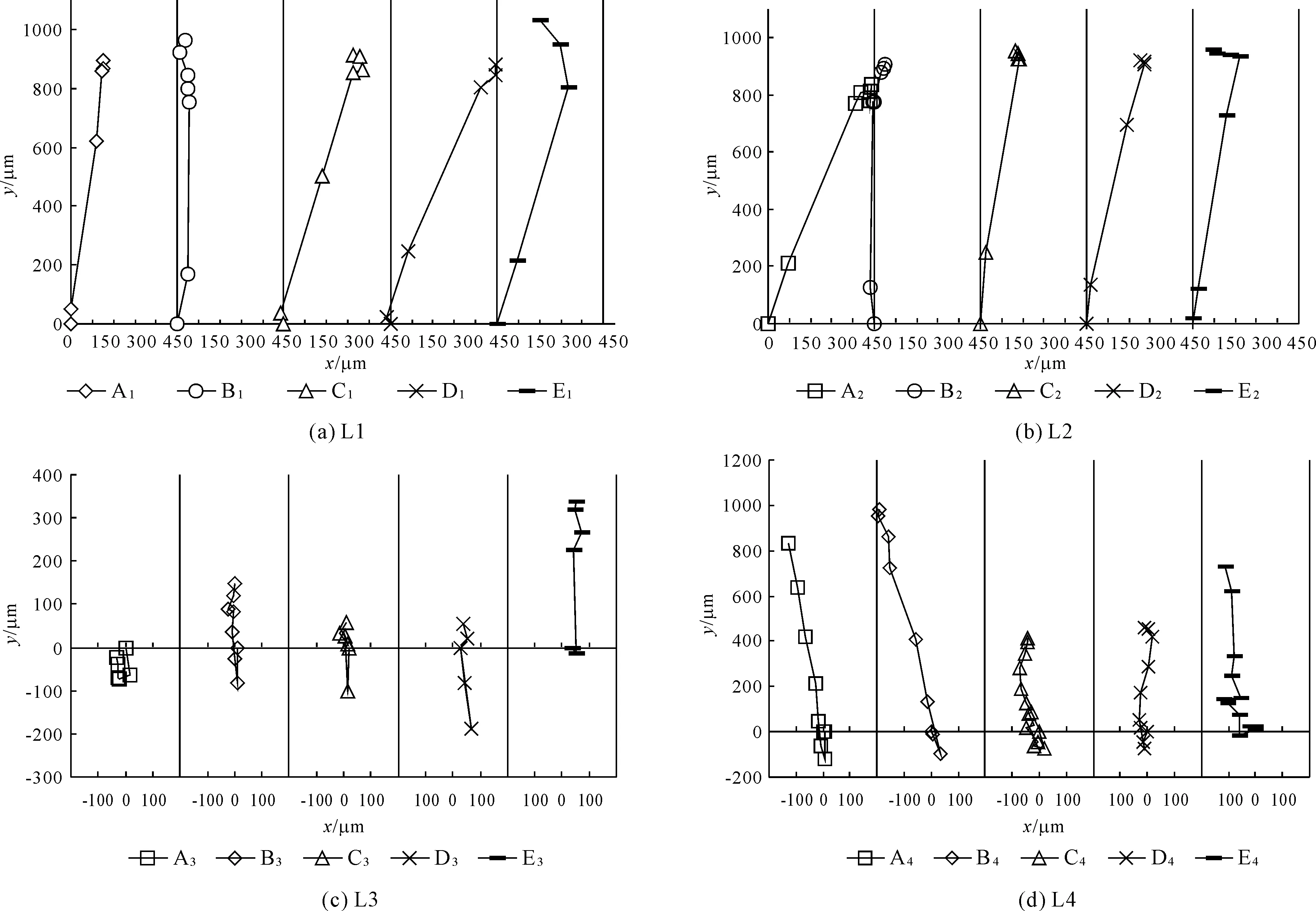
图6 试验组L1—L4玻璃珠移动轨迹
为量化液桥力,将图6中颗粒的等时间间隔位移信息通过牛顿第二定律转化后得到等时间间隔内的平均液桥力与时间的关系曲线,见图7(单粒直径2 mm玻璃珠的质量为10.26 mg)。
图7中液桥力“F”的值为正表示液桥力对玻璃珠做正功,反之则做负功。实验组L1、L2因接触点无液滴,试验条件较易控制,因此各重复试验的相似度较高,液桥力整体以震荡的形式呈现出急速衰减的趋势。
从试验数据看,试验设置的液桥流速对吸湿过程中的液桥作用力的峰值大小关系不大。试验组L1、L2玻璃珠所受的峰值液桥力约为20 μN。试验组L3、L4的峰值液桥力在8 μN以内。玻璃珠初始时是否被湿润,对液桥力的影响较大。

图7 液桥力-时间关系图
从总体的曲线形态来看,液桥力随时间的变化曲线都以F=0为基准线上下波动,并在初期有短暂的增长趋势,但随后迅速衰减。这一趋势将在第3节进行分析。
3 液桥作用机理
3.1 液桥力理论分析
试验过程中的液桥是动态变化的,因此需考虑动态液桥力。动态液桥力由两部分构成—静态液桥力及动态黏性力,需对其单独分析[3]。
动态黏性力Fvis可由雷诺方程表示[3],Fvis的大小与颗粒半径、液体的黏性系数、颗粒间距、颗粒移动速度等参数有关。
对两光滑球颗粒间液桥力,大多采用下式进行计算[31]:
F=2πRγsinβsin(θ+β)-ΔPπR2sin2β
(1)
(2)
ΔP一般通过Young-Laplace方程(2)表征,r为液桥最窄颈部的半径,γ为液桥的表面张力系数,R1、R2分别为两颗粒的半径;θ1、θ2分别为两种颗粒与孔隙液体的接触角;β1、β2分别为液滴对两颗粒的半填充角,其值小于90°;r1、r2为液滴曲面的一对主曲率半径(见图8)。
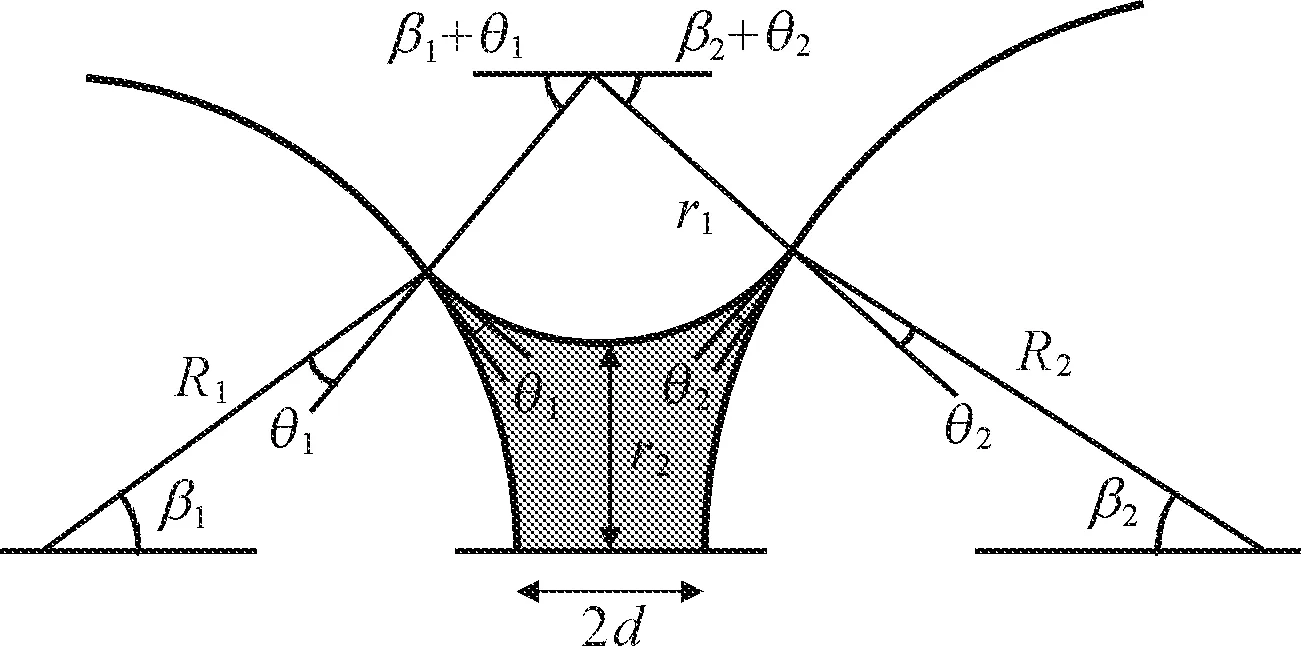
图8 光滑不等径球形颗粒液桥模型
通常认为当β<90°,θ<90°时,液桥衡对颗粒有吸引作用。
上述公式(1)中的基质吸力ΔP为一个大于零的值,即公式(1)仅适用于“气-液”界面处气压大于水压的情况。颗粒群的吸湿脱湿过程中还包存在“气-液”界面处的气压小于水压的情况(如图9所示)。因此将公式(1)进行推广:由几何关系可知,仅当β>π-θ时,ΔP<0。此时的液桥力的计算公式(3):
F″=-2πRγsinαsin(α-θ)-ΔPπR2sin2α
(3)
α为颗粒的“气相半填充角”(0°<α≤90°)。在数值上β=π-α。为方便比较,将公式(1)中的β称之为颗粒的“液相半填充角”。当F″小于零时玻璃珠有被液桥吞没的趋势,反之则有被推离液桥的趋势。
通过公式(3)易知,当θ≤α<90°时,F″恒小于零;θ=α时,为液体表面张力对液桥作用力的贡献度为零。当α∈[0,π/2]时,函数F″恒为关于α的单调递减函数,因此当存在零点α0且α<α0时,F″恒大于零,玻璃珠在液桥力下有被拖入液桥的趋势;同理,α>α0时F″恒小于零,玻璃珠在液桥力下有被推离液桥的趋势。因此,在液桥推移速率适当的情况下,玻璃珠以“气-液”界面为基准面,以“振动”的方式随液桥迁移。
在考虑动态黏性力产生的阻尼作用后,迁移阶段的玻璃珠的迁移方式应修正为以“气-液”界面为基准面的“有阻尼振动”(见图10,短箭头表示玻璃珠所受的液桥力方向,长箭头表示液桥推移方向)。
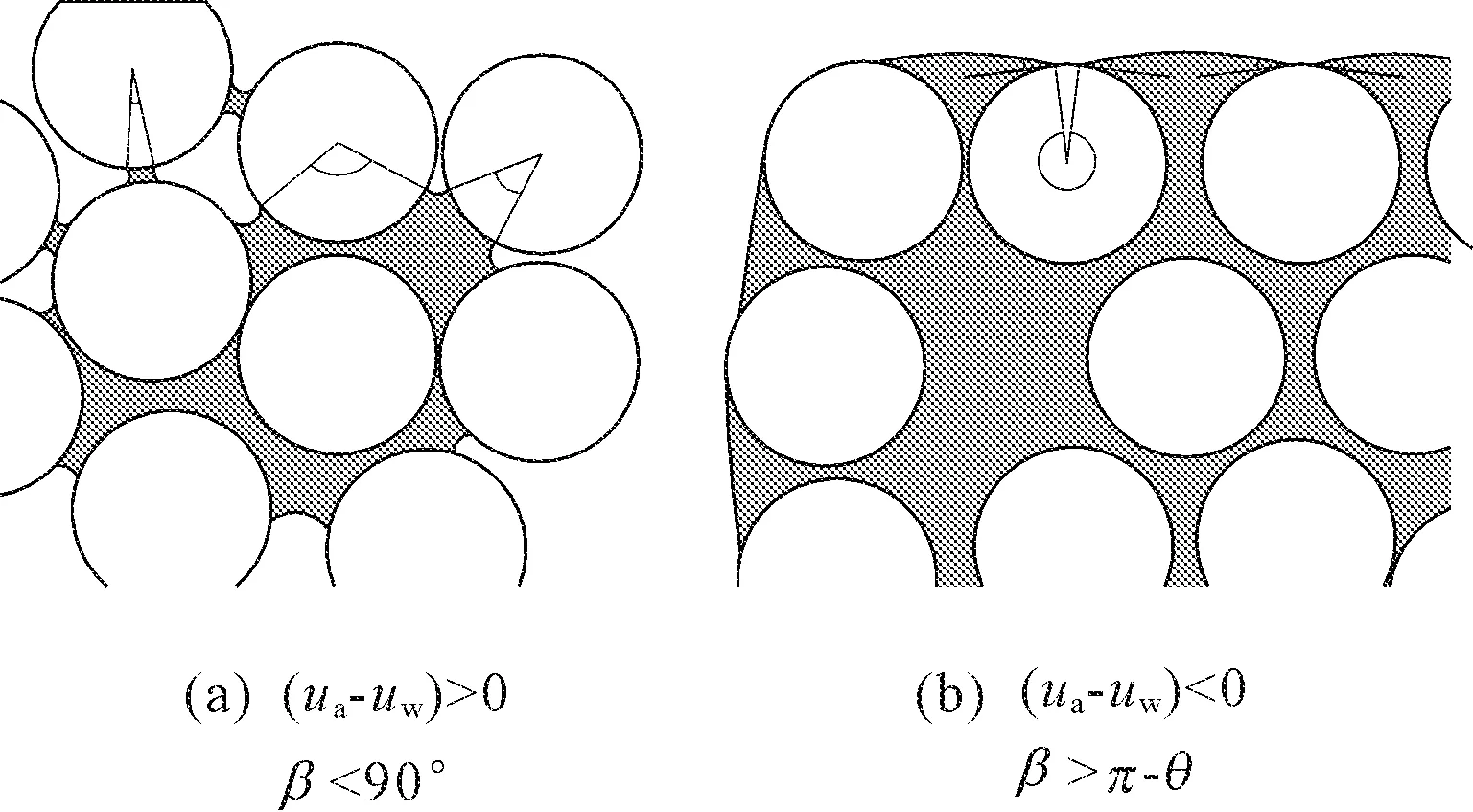
图9 液桥概化模型
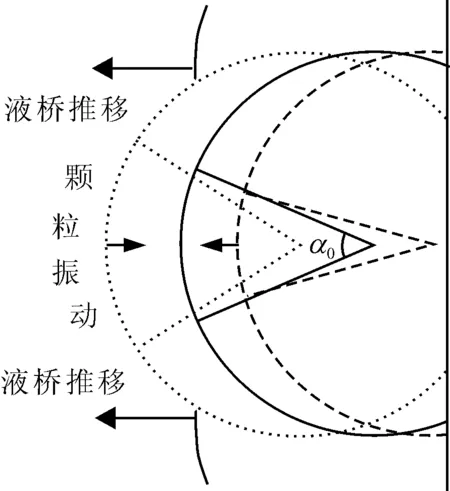
图10 液桥力作用下的颗粒迁移示意图
3.2 干湿循环过程中的液桥作用机理
在3.1节的理论基础上可对第2章中的试验现象进行深入分析。
在单颗粒试验中,液桥的半填充角都小于90°,可以使用公式(1)对液桥力进行定分析。公式(1)中液桥力衡大于零,这与图7显示的液桥力在试验过程中正负交替变化的规律不相符。因此可以推断,在这个过程中动态黏性力起到了重要作用。动态黏性与玻璃珠的相对运动速度有关,玻璃珠速度越快动态黏性力越强。
在颗粒群试验中,脱湿试验比吸湿试验对颗粒结构的影响要大得多,其机理如下:
(1) 吸湿过程是一个由饱和区向非饱和区扩张的过程,液桥力瞬时递增然后在短时间内迅速递减。从单颗粒试验的轨迹看,玻璃珠的运动轨迹长度与粒径的比值约为0.15~0.50,这个比值随颗粒群的初始含水率而逐渐减小。且这一阶段的完成时间约在0.1 s~0.2 s之内。
(2) 吸湿过程中液桥的局部推移速率时刻都在产生波动,因为湿润过程中液桥的接触角等因素基本不呈定值[32-35]。尤其对于处于颗粒群边缘的颗粒,一旦局部流速加快,处于临界半填充角的玻璃珠可能会被瞬间吞没。
(3) 脱湿过程是一个由非饱和区向饱和区扩张的过程,玻璃珠的填充角随吸湿逐渐减小。液桥力的值在脱湿过程中先逐渐增大然后逐渐减小。这个过程非常缓慢,室温下往往要数日。脱湿过程不受临界填充角的影响。
4 结论及展望
(1) 推广得到了ΔP<0时光滑球形颗粒的液桥作用力的理论计算公式(3),依此对文中玻璃珠随液桥迁移的运动机理进行了定性分析。认为玻璃珠在处于临界半填充角时,且液桥推移速率适当的情况下,玻璃珠以“气-液”界面为基准面,以“有阻尼振动”的方式随液桥迁移。
(2) 从试验以及理论分析的角度,得出了干湿循环对颗粒扰动总体发生在第一次干湿循环这一现象的细观机理。吸湿过程是个液桥力瞬间增大然后减小的过程,这个过程中液桥力变化迅速,在0.1 s~0.2 s之内便无法对颗粒位移造成显著影响。当湿润过程中填充角达到临界值时,液桥极易因流速变化而吞没颗粒,而无法继续对颗粒施加影响。脱湿过程液桥力逐渐增加随后逐渐减小,该过程持续时间长,液桥存在期间都对颗粒施加有拖曳力。
