大跨度悬索桥疲劳受力特征及损伤规律

王丽 朱颖 郭辉 胡文军

（1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081；3.中铁大桥勘测设计院集团有限公司，武汉 430056）

随着桥梁建造技术的不断进步，我国具备了建造千米级大跨度桥梁的能力，近年来先后建成了沪苏通铁路长江大桥、五峰山长江大桥等主跨超过1 000 m跨度的桥梁［1-2］。大跨度铁路悬索桥加劲梁的疲劳问题比较突出，目前还未见相关资料对大跨度悬索桥杆件的疲劳损伤规律和特征进行研究。另外，现行规范中部分疲劳设计参数是基于既有中、小跨度桥梁确定的［3］，对于大跨度桥梁是否适用需要进一步研究。

本文以我国一座主跨1 060 m 的悬索桥为研究对象，对桥上不同类型杆件的疲劳受力特征和损伤规律进行系统的计算分析，掌握大跨度悬索桥不同类型杆件的疲劳损伤情况，为疲劳设计参数的制定提供支撑。

1 桥梁概况

大桥主缆跨度布置（图1）为（245+1 060+270）m，主梁跨度为（130+1 060+90）m，加劲梁全长1 280 m。主桥为钢桁梁结构，桥面系为密布纵横梁体系。纵横梁桥面系在上联结系平面内（图2）。

图1 计算主桁杆件和纵横梁（单位：m）

图2 桥梁联结系

大桥按照双线客货共线铁路进行设计，设计速度200 km/h，列车荷载图式为ZKH 荷载［4］。其所在线路货物列车主要开行集装箱班列，同时考虑开行棚车、其他类型普通货物列车等；旅客列车采用动车组和机车牵引客车混跑模式。桥上运营列车种类见表1。

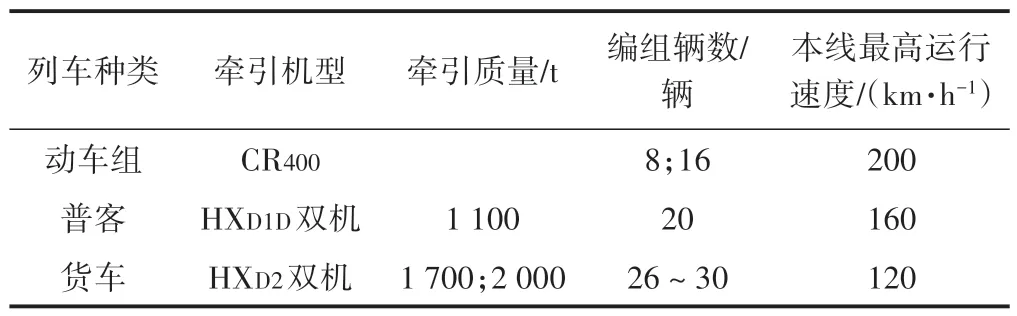
表1 桥上运营列车种类

2 疲劳受力特征

建立全桥有限元模型，对单线ZKH 列车荷载作用下主桁杆件、纵横梁、联结系等杆件的疲劳受力特征进行分析。为避免杆端模拟误差对杆件应力的影响，应提取杆件中间的应力。由于受压杆件不考虑疲劳问题，所以绘制应力变程分布特征图时受压杆件按应力变程为0处理。

2.1 主桁杆件疲劳受力特征

主桁竖杆为局部受力杆件，杆件受力比较均匀，应力变程整体较小，故未予示出；横向中间竖杆为受压杆件，不存在疲劳问题。主桁杆件应力变程分布特征见图3。

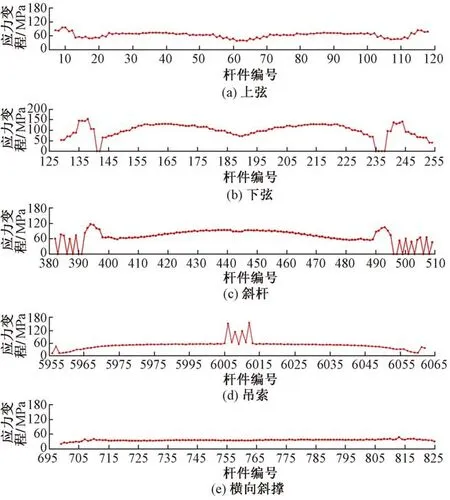
图3 主桁杆件应力变程分布特征

在主跨和边跨跨中位置，上弦为受压或以受压为主的拉-压杆件，下弦为受拉或以受拉为主的拉-压杆件；在塔根及主跨靠近塔根的区段，由于负弯矩的存在，上弦主要为受拉或以受拉为主的拉-压杆件，下弦为受压或以受压为主的拉-压杆件。由图3（a）和图3（b）可知，上下弦均是塔根位置的应力变程最大，下弦的应力变程整体上大于上弦，最大值为153 MPa。

边跨斜杆主要为受拉或以受拉为主的拉-压杆件；主跨跨中约9个节间的区段以受拉为主，其余位置以受拉为主和以受压为主间隔出现。由图3（c）可知，应力变程最大的斜杆位于第2，3 根吊索之间（从左侧梁端数起），其值为116 MPa。

竖向吊索均受拉，斜吊索包括受拉和以受拉为主2 种受力情况。由图3（d）可知：竖向吊索应力变程两侧较小，中间较大，应力变程最大值为63 MPa；斜吊索应力变程最大值为153 MPa，为竖向吊索的2.4倍。

横向斜撑为受拉杆件。由于其为局部受力杆件，由图3（e）可知，不同位置杆件的应力变程相差不大，其值在20～46 MPa，多数杆件应力变程为30～40 MPa。

2.2 纵横梁疲劳受力特征

梁端到1/2 边跨位置的纵梁承受弯曲应力，下缘受拉、上缘受压；其他位置纵梁同时承受轴向应力和弯曲应力，且竖向弯曲为上下反复弯曲。中纵梁的应力变程整体大于边纵梁，最大应力变程出现在主跨1/4位置上翼缘，为90 MPa。

上横梁除端横梁外，在节点跨中位置均向上弯曲，其中第2 个节点横梁（从左侧梁端数起）上翼缘的应力最大，为73 MPa；节间横梁受力相对复杂，第1 个节间横梁（从左侧梁端数起）向下弯曲，塔根位置到主跨1/4 跨之间有一部分横梁向下弯曲，其余均上下反复弯曲，应力变程最大值为82 MPa。下横梁应力变程整体较小，大部分应力变程不超过20 MPa，其中主塔左右两侧横梁最大，其值为38 MPa。

2.3 联结系疲劳受力特征

上联结系斜撑除边跨部分杆件为受压或受拉杆件之外，其余主要为以受拉为主或以受压为主的拉-压杆件。塔根位置应力变程比其他位置略小，应力变程最大值为82 MPa，位于第3根和第4根（从左侧梁端数起）吊索之间。

下联结系斜撑受力方式与上联结系斜撑相似，除边跨部分杆件为受拉杆件外，其余主要为以受拉为主或以受压为主的拉-压杆件，应力变程整体小于上联结系斜撑，最大值为47 MPa，位于第1 根吊索处（从左侧梁端数起）。

下联结系纵向撑杆虽为受拉或以受拉为主的拉-压杆件，但除端部一根杆件应力变程稍大之外，其余杆件应力变程均较小，不超过5 MPa。

该桥在主桁两侧设有竖向斜撑。其中，中间斜撑为受压杆件，两侧斜撑为受拉杆件，应力变程最大值为43 MPa。

3 疲劳损伤规律

3.1 计算方案

选择HXD2双机牵引P70货车作为加载列车，HXD2机车和P70货车的轴重和轴距见图4。编组方式考虑2种工况：工况1 为32 节P70 货车全部满载，列车总长564.902 m；工况2 为64 节P70货车按一节空载一节满载的方式进行加载，列车总长1 091.814 m。

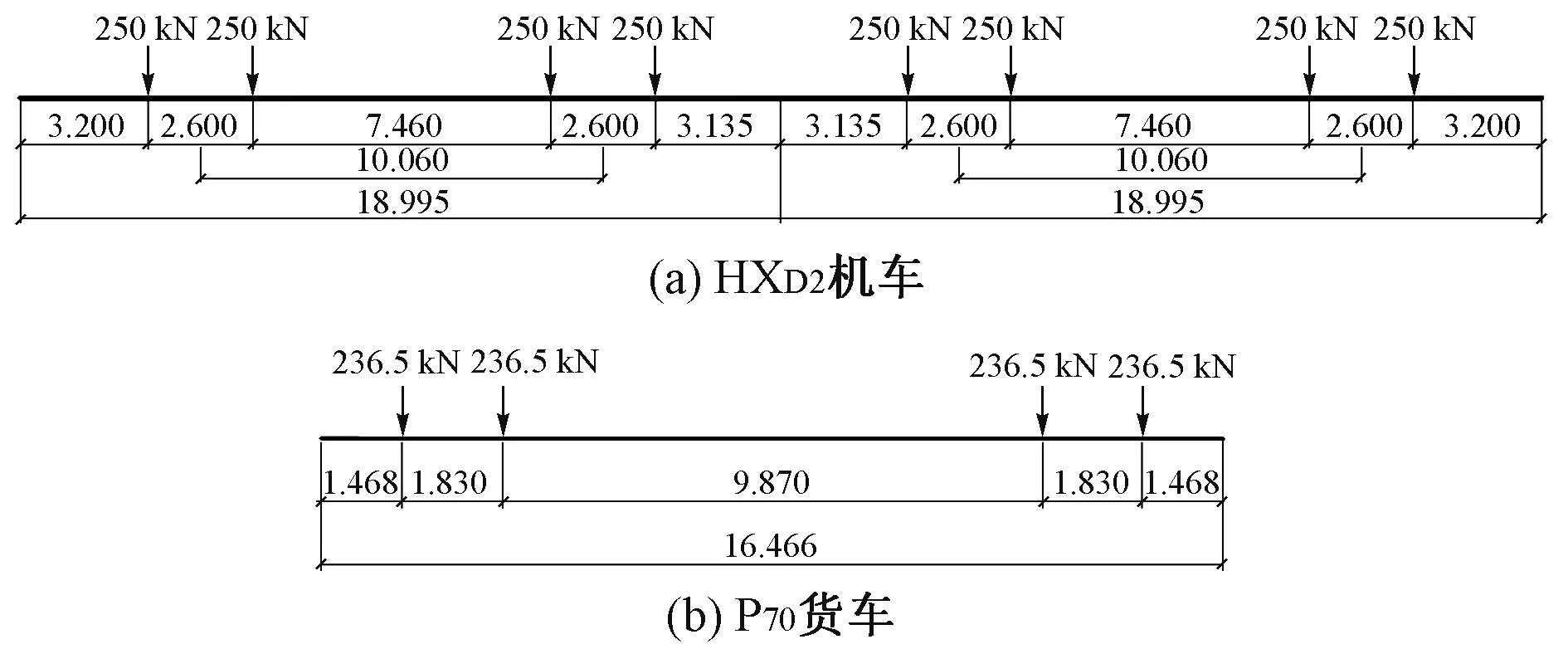
图4 HXD2机车和P70货车轴重和轴距（单位：m）

选择典型位置（包括边跨、塔根、主跨1/4 跨），主桁杆件（包括跨中上弦、下弦、斜杆和吊索），以及应力较大的纵横梁进行计算分析，见图5。

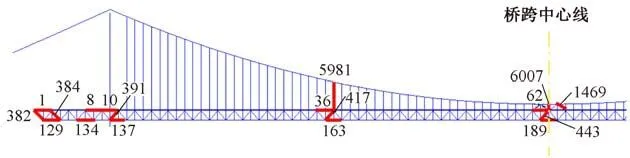
图5 计算主桁杆件和纵横梁位置及编号

首先计算得到列车经过桥梁时典型杆件的应力历程，然后采用雨流法对不同杆件的应力进行统计分析得到应力频谱，即不同应力变程等级下的循环次数。将应力变程按10 MPa为一个等级进行划分，最后按照下式计算不同杆件的损伤度。其中0～10 MPa等级应力变程一般处于疲劳截止限以下，在计算损伤度时不予考虑，仅考虑10 MPa以上的应力变程。

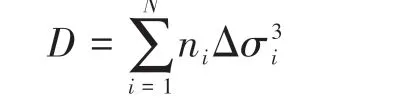
式中：D为损伤度；Δσi为疲劳列车引起的应力变程，MPa；ni为Δσi对应的循环次数；N为应力变程等级数量，按每10 MPa为一个等级进行划分。

3.2 不同类型杆件损伤度的对比分析

工况1 中列车通过桥梁时，计算主桁杆件和纵横梁的损伤度，见图6。可知：①对于主桁杆件，下弦损伤度最大的杆件位于塔根处；上弦损伤度最大的杆件位于边跨处；斜杆损伤度最大的杆件位于主跨跨中。由于吊索是局部受力杆件，因此不同位置的损伤度基本相同；斜吊索的损伤度较大，显著大于竖向吊索。②对于主桁杆件，塔根处下弦的损伤度最大，其次为斜吊索。对于纵横梁，中纵梁的损伤度大于边纵梁，节间横梁的损伤度大于节点横梁，节间横梁的损伤度最大。③由于纵横梁为局部受力杆件，影响线较短，损伤度的最大值显著大于主桁杆件。

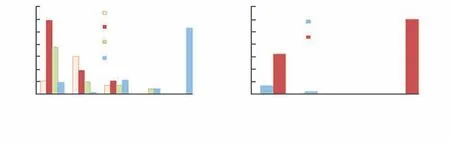
图6 主桁杆件和纵横梁损伤度

3.3 列车编组方式对杆件损伤度的影响分析

计算工况2 中主桁杆件和桥面系的损伤度［5］，并与工况1 进行对比，以掌握列车编组方式对于桥梁杆件损伤度的影响特征。

3.3.1 主桁杆件

工况2 与工况1 主桁杆件损伤度的比值见表2。可知，对于主桁杆件，工况2 比工况1 损伤度小。这是因为该桥主桁杆件同符号影响线长度在500 m 以上，列车延米重对杆件的内力影响较大。在列车总载重不变的情况下长度增加，单位长度内的重量减少，则杆件应力变程减小，而应力循环次数基本不变，因此损伤度减小。

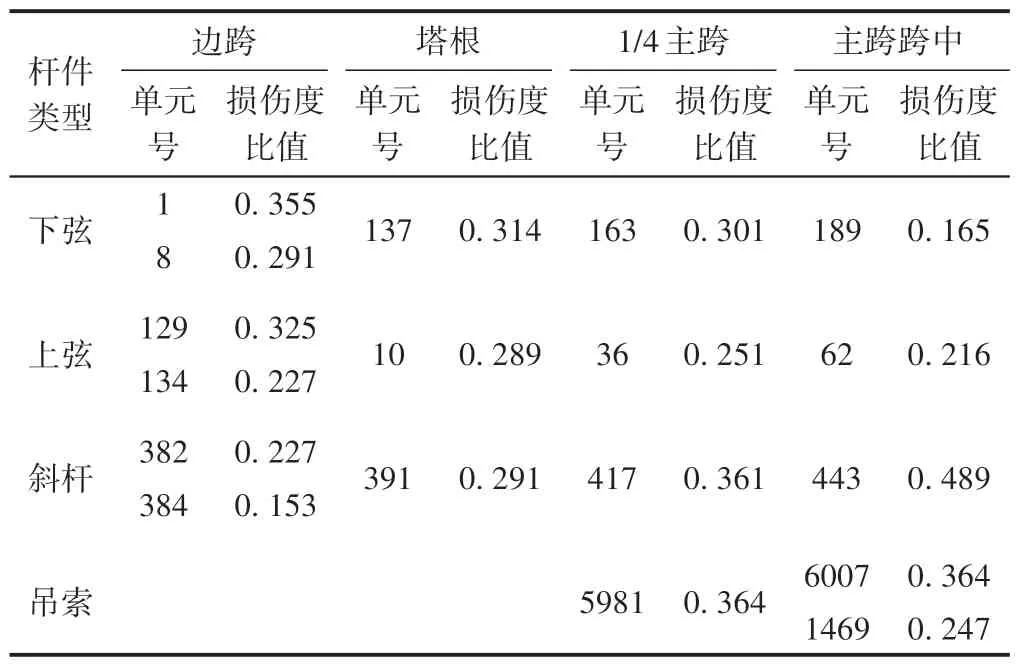
表2 工况2与工况1主桁杆件损伤度的比值

3.3.2 纵横梁

工况2 与工况1 纵横梁损伤度的比值见表3。可知：对于中纵梁下翼缘和节间横梁上翼缘，工况2的损伤度略大于工况1；对于边纵梁，工况2 的损伤度小于工况1；对于节点横梁，工况2 的损伤度与工况1相同。2 种工况下中纵梁和横梁的损伤度相差不大。这是因为对于影响线较短（10～20 m）的杆件来说，当列车经过时，大约一节或一节半车便引起一次应力循环。当列车编组长度增加时，应力变程没有变化，损伤度受应力变程的影响较大。

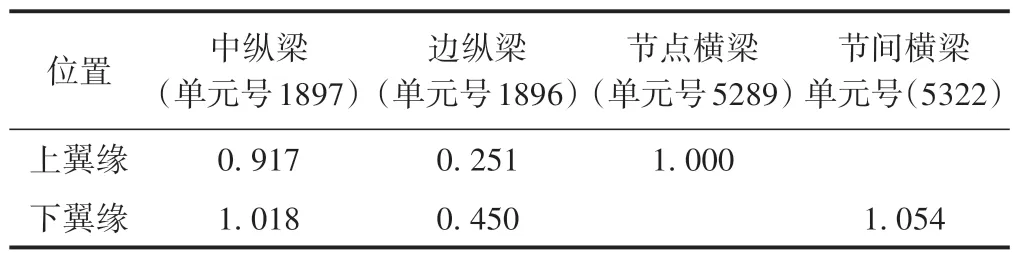
表3 工况2与工况1纵横梁损伤度的比值

4 结论

1）从疲劳受力特征来看，传统简支钢桁梁的上下弦杆件为受拉或受压杆件，斜杆为以受拉为主或以受压为主的杆件，纵横梁按受弯杆件考虑。而大跨度悬索桥的主桁杆件中，无论上弦还是下弦，大部分为拉-压受力杆件，上弦以受压为主的杆件居多，下弦则以受拉为主的杆件居多。大跨度悬索桥密布纵横梁体系与传统的纵横梁体系受力也有所差别，除受弯曲应力之外，还承受一定的轴向应力。

2）从疲劳应力变程的大小来看，主桁杆件上下弦在塔根位置的应力变程较大，斜杆在第2，3 根吊索位置的应力变程较大，吊索在跨中位置的应力变程较大，纵横梁约在1/4主跨位置应力变程较大。

3）从疲劳损伤度来看，主桁杆件中塔根下弦的损伤度最大，应力变程最大；中纵梁和横梁由于影响线较短，列车经过时应力循环次数多，因此虽然应力变程小于塔根下弦，但疲劳损伤度较大。

4）在载重相同的情况下，列车编组长度对影响线较长的主桁杆件影响大，列车长度越长则损伤度越小；列车编组长度对影响线较短的局部受力杆件影响小。

本文对于杆件局部的受力特征未予涉及，例如竖杆杆中应力变程不大，但杆端次应力较大，仍然存在疲劳问题。因此，对于局部构造细节的疲劳问题，还需要结合细部计算结果进行合理的分析和判断。