脱空对刚性道面板应力分布的影响及临界脱空状态

赵鸿铎，曾孟源，吴荻非，凌建明，韦福禄

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.同济大学民航飞行区设施耐久与运行安全重点实验室，上海 201804；3.中国建筑第八工程局有限公司工程研究院，上海 200122）

在服役过程中常由于冲刷、沉降等原因，导致机场刚性道面板底层间材料局部流失而形成空隙。由于环境和重复荷载耦合作用，空隙逐渐发展为板底脱空［1］，使得基层对道面板的支承作用发生显著劣化，严重影响道面板受力状态并易引起应力集中，从而诱发断板、错台等病害，危害刚性道面结构性能［2］。因此，及时、准确地评定板底脱空，对保障机场道面结构健康具有重要意义。

20世纪20年代起，陆续有学者通过理论公式推导，开展脱空影响下道面板力学响应分析，并提出局部脱空下道面板角、板边应力的经验公式［3］。然而，劣化后的支承状态较复杂，依托简化、主观的经验公式难以真实表达脱空形态，无法保证脱空影响分析的准确性。随着有限元分析技术的不断成熟，数值仿真逐渐成为分析刚性道面板脱空影响的主流方法。刚性道面板底支承主要表现为基层对道面板的持力作用，因此在数值建模过程中常采用减小地基回弹模量［2］、直接构造空隙［4］、移除层间接触［5］等方式表达脱空形态。周玉民等［4］采用不同地基模型和车辆荷载分析路面板脱空下的荷载应力后发现，板角脱空导致板内应力增幅达1.0～3.6倍。苗禄伟［6］进一步考虑接缝传荷性能的影响，发现接缝传荷性能越好，脱空对弯拉应力、表面弯沉的影响越不明显，而在接缝刚度较低时，脱空导致板内弯拉应力增幅达2 倍以上。研究还表明，脱空会对道面表面弯沉产生显著影响［7-9］，表面弯沉会随着脱空程度加剧而明显增大。据此，中国与美国的机场刚性道面规范均采用弯沉类指标以评定板底脱空影响［10-13］。

总体而言，数值仿真法相较于理论求解法能够更精细地模拟支承状态，但仍存在以下不足之处：地基模量折减法主要适用于弹性地基上的单层板模型，对面层与基层的支承状态描述不足；直接构造空隙对局部有限元网格要求较高，易导致不收敛；移除层间接触则需引入库伦摩擦模型，大幅度增大运算代价。因此，近年对脱空的影响分析主要聚焦于荷载应力的大小与增幅，并且仅局限于板底荷载应力［14-16］，对脱空导致的应力重分布以及其引发的板顶荷载应力变化考虑不足。在脱空评定方面，现有弯沉法受限于理论推导的繁琐以及仿真模拟的高运算量负荷，对不同接缝传荷性能、飞机荷载形式下的脱空影响分析还存在一定不足，同时既有弯沉类指标的评定阈值主要依靠经验选取，尚无明确的临界脱空状态定义。因此，在上述研究基础上依托层间弹簧单元提出了支承状态精细化模拟方法，可在保障准确性的同时提高数值仿真计算效率。考虑不同飞机荷载类型、接缝传荷性能，探究脱空影响下的荷载应力重分布规律。根据数值仿真结果提出刚性道面板临界脱空状态，并与现行规范进行对比以检验其适用性。

1 数值仿真模型

1.1 道面板模型

现行混凝土道面设计规范常将刚性道面结构简化为Winkler地基上的单层板模型，以避免构造实体地基单元，影响计算效率。朱立国［17］进一步比较Winkler地基上单层板模型与双层板模型后发现，两者均可有效模拟刚性道面结构响应，并且双层板模型能更准确地表达道面板底支承状态。因此，选用Winkle地基上的双层板模型建立刚性道面三维数值仿真模型，如图1a所示。

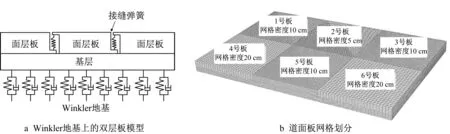
图1 刚性道面板三维数值仿真模型Fig.1 Three-dimensional numerical simulation model of concrete pavement slab

为模拟板间接缝状态，建立6块板模型，如图1b所示。2 号板为分析板块，用于模拟不同支承状态，而其余板块用于模拟不同板间接缝状态。模型结构参考实际工程中的典型道面板结构，单块道面板尺寸为5.0 m×5.0 m×0.4 m，基层尺寸与6块板整体尺寸匹配，为10.0 m×15.0 m×0.4 m。6块板模型的网格类型均采用C3D8R，其中2号板为分析板块，网格密度最小，为5 cm；1、3、5号板和基层的网格密度为10 cm，4、6 号板的网格密度则为20 cm。通过层次化的网格密度，既可保障板块（2 号板）分析精度，又可避免计算量过大。对于接缝传荷性能的模拟，依据周正峰等［18-19］提出的弹簧单元模拟方法，在接缝处部署竖向弹簧单元以模拟竖向传荷能力，如图1a所示。接缝弹簧刚度ka计算式如下所示：

式中：λ为接缝长度，m；q为接缝刚度，N·m-2；NR、NC分别为接缝截面弹簧节点行数和列数。

1.2 荷载模型

（1）飞机荷载

我国飞机主起落架轮轴可分为单轴双轮（代表机型A320）、双轴双轮（代表机型A330）和三轴双轮（代表机型A380）等，如图2 所示。道面结构数值仿真模型的网格多采用方形网格，故常假定轮印形状为矩形，并且机轮与道面接触为均匀分布，据此选用的3种起落架构型及荷载参数如表1所示。另外，通过定义多个分析步遍历荷载移动路径上的作用位置，模拟移动飞机荷载并定位临界最不利荷载位置，定义方法如图2所示。

（2）冲击荷载

采用冲击荷载模拟重型落锤式弯沉仪（HWD）测试时的荷载激励，以捕获道面板模型的表面弯沉。在施加荷载激励时，落锤先自由落体，而后撞击橡胶垫块，完成单次激励加载。采用半正弦波式的冲击荷载模拟该激励，并通过Abaqus 软件中Amplitude模块设置2个荷载级位，相关参数如表2所示。

图2 飞机荷载模拟方法Fig.2 Simulation of aircraft load

表1 飞机荷载参数Tab.1 Parameters of aircraft load

表2 冲击荷载参数Tab.2 Parameters of impact load

1.3 支承状态模拟

Chun 等［20］在多层沥青路面结构的数值仿真中提出一种基于阵列式弹簧单元的接触状态模拟方法，采用阵列式弹簧单元连接各路面结构层，通过调整弹簧单元刚度模拟不同接触程度。该弹簧模型相较于传统的库伦摩擦模型［17］，可精细化模拟复杂接触状态，并且运算代价更低。在此基础上，进一步提出基于层间弹簧模型的刚性道面板底支承状态模拟方法，通过Abaqus软件中的竖向弹簧单元定义层间弹簧模型，如图3a所示。对于脱空区域，可移除该区域层间弹簧以模拟支承作用劣化，如图3b所示。层间刚度kb依据下式计算：

式中：E为基层弹性模量，MPa；S为接触压力作用面积，m2，通常取面层面积；h为接触压力作用深度，m，通常取0.01 m；n为弹簧节点数。

为验证弹簧模型的准确性，将其与库伦摩擦模型对比，分别计算2 种方法在相同飞机荷载作用下的表面弯沉与板底最大弯拉应力，计算结果如图3c所示。可以发现，2 种方法所得弯拉应力、弯沉的分布规律基本一致，但弹簧模型的弯拉应力极值稍大于库伦摩擦模型结果，差异值在5%以内；同时，由于弹簧单元的影响，变形的分布曲线存在一定波动，但计算差异也在5%以内。此外，2种模型在计算代价上存在显著差异：对相同分析模型（约20 万个分析单元），采用弹簧模型的单次计算耗时约为90 s，而采用库伦摩擦模型则耗时达1 800 s 以上；库伦摩擦模型对网格划分要求高，在模拟复杂、不规则的支承状态时易发生不收敛。因此，综合考虑两者差异及计算便利性，采用弹簧模型模拟板底支承作用，通过改变不同位置的弹簧单元刚度，构造不同范围、不同程度的脱空。

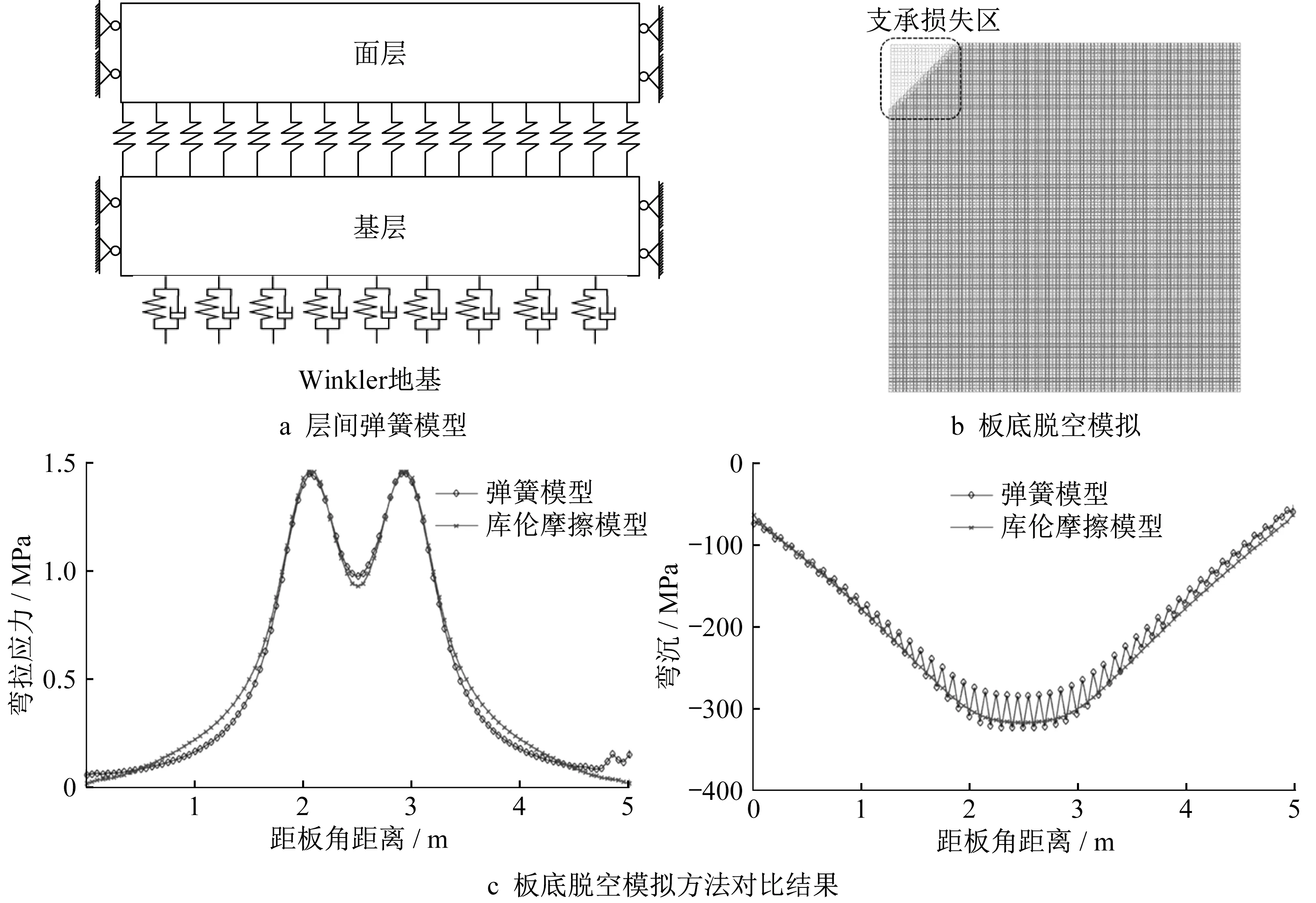
图3 支承状态模拟Fig.3 Simulation of support condition

1.4 模型参数

为确定数值仿真模型参数，在某机场道面试验区开展足尺验证。试验区内包含多块水泥混凝土道面板，单板尺寸为5.0 m×5.0 m×0.4 m，接缝处设置传力杆，以模拟真实的刚性道面板接缝状态。为确定并验证道面结构的模型参数，利用大型卡车的轴载模拟飞机荷载，通过对比实测力学响应和模拟的力学响应以确定数值仿真模型参数。试验位置和加载车辆如图4a 所示。后轴为双联轴，胎压为1.2 MPa，车轴质量为38.05 t，车辆移动速度为0.7 m·s-1，轴距为1.35 m，轮距为0.30 m。同时，在横缝中部埋设应变计测量道面板力学响应。此外，依照足尺试验中道面板实际尺寸、真实荷载激励形式建立对应数值仿真模型，提取横缝中部处的力学响应结果并与实测值进行对比，不断修正仿真模型的参数取值。数值仿真模型参数如表3所示。

图4b为数值仿真模拟结果与实测结果的对比。可以发现，模拟结果与实测结果两者随时间变化趋势一致，并且均出现2个波峰，分别对应双联轴前后2 个车轴施压。虽然由于道面平整度、荷载随机性、仪器测量误差等因素导致2条曲线峰值存在一定差异，但是差异在0.5 MPa以内，一定程度上证明该模型参数取值的合理性。

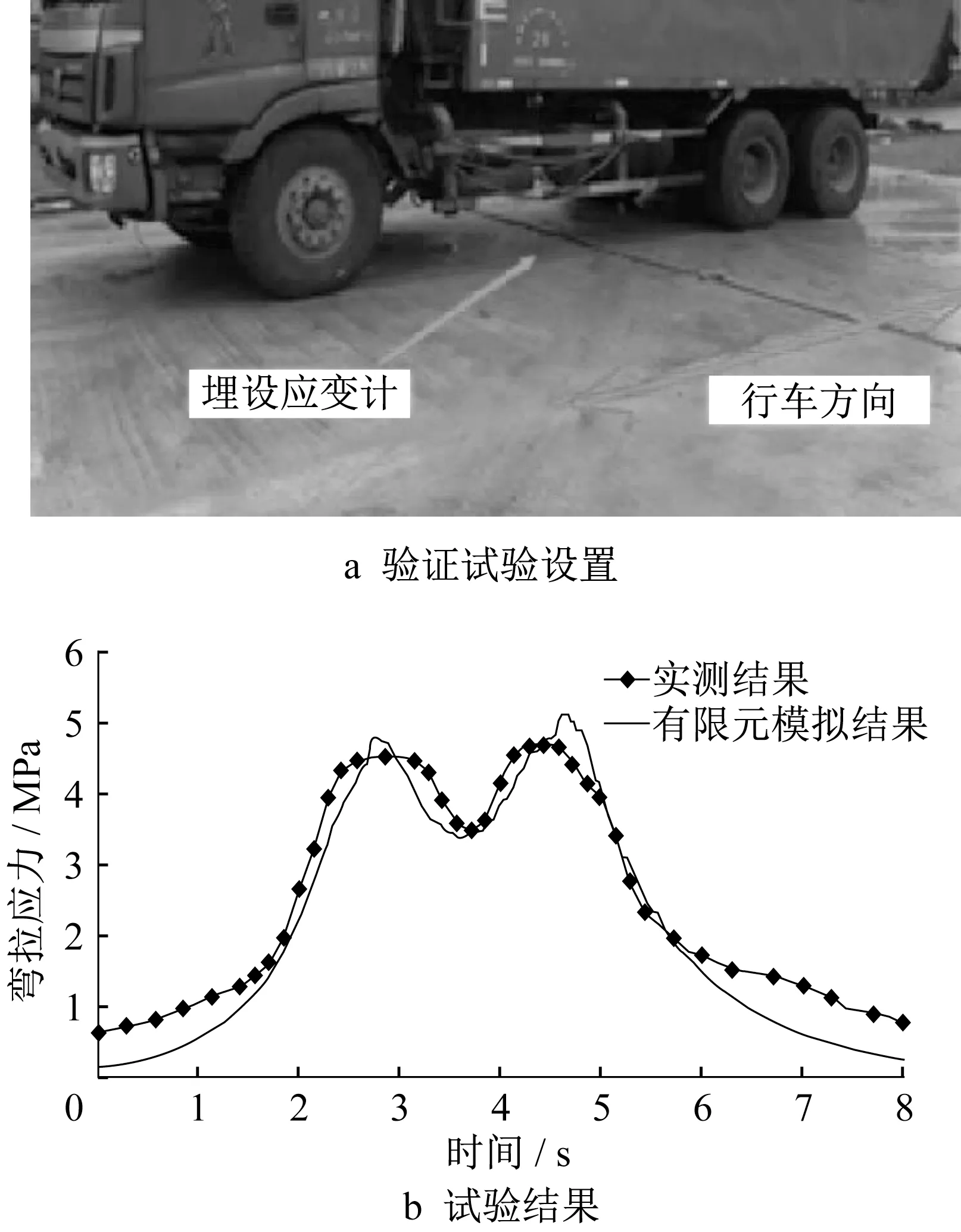
图4 足尺试验验证Fig.4 Full-scale test for verification

2 脱空影响下的刚性道面板应力分布

2.1 支承状态工况

为分析支承状态影响下的刚性道面板应力分布，利用数值仿真模型模拟不同支承状态，考虑不同程度的板角脱空、板边脱空，建立60个分析工况，如表4、5所示。其中，板角损失形状为三角形，板边损失形状为矩形。通过调整接缝弹簧刚度，模拟6 种不同接缝传荷系数（66%～96%）。每个分析工况，均施加A320、A330 和A380 等3 种不同机型的飞机荷载。

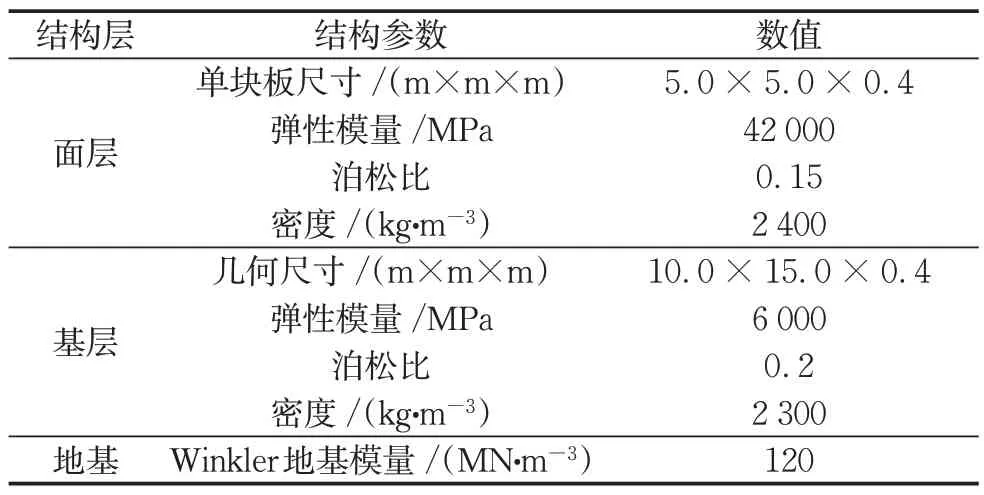
表3 数值仿真模型参数Tab.3 Parameters of numerical simulation model

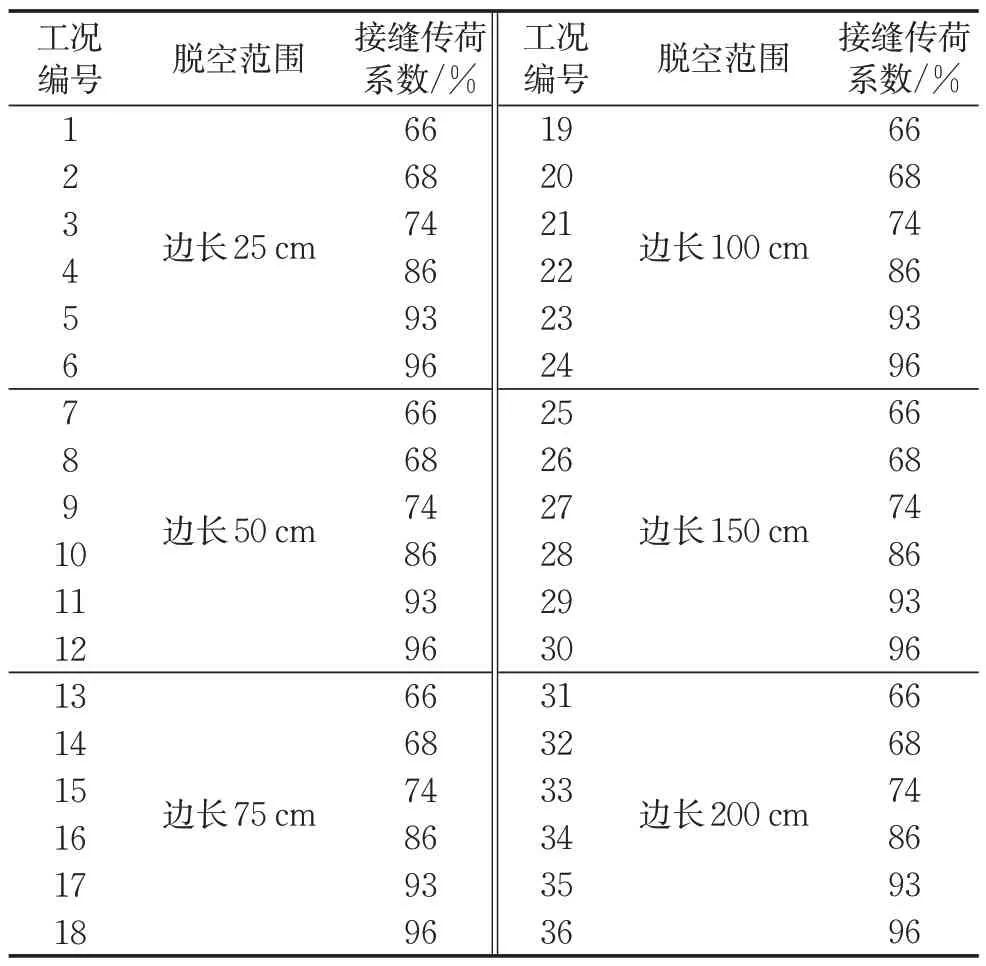
表4 有限元分析工况（板角脱空）Tab.4 Scenarios of finite element analysis (supportloss in corner)

2.2 多工况求解

由于求解工况量较大，并且需要不断调整支承状态、接缝传荷系数、荷载类型等系列参数，若采用Abaqus 软件自带的可视化界面进行参数设定、工况提交、结果提取等工序，操作繁琐且低效，因此通过脚本文件（INP 文件）批量生成上述工况，并自动提取模型计算结果，实现数值仿真模型多工况快速分析。INP 文件中包含仿真模型的结构、材料、接触、边界条件、分析步等信息。图5a 展示了采用的INP文件结构。*Part主要包含道面板节点、单元编号及对应的位置信息；*Assembly 为模型装配步，包含模型实例信息、节点集信息、单元集信息；*Material 为结构材料参数，包括弹性模量、泊松比、密度等；*Boundary 和*Foundation 为模型边界条件；*Step 为分析步，包括分析方法、时间步长以及分析时间的设定等。

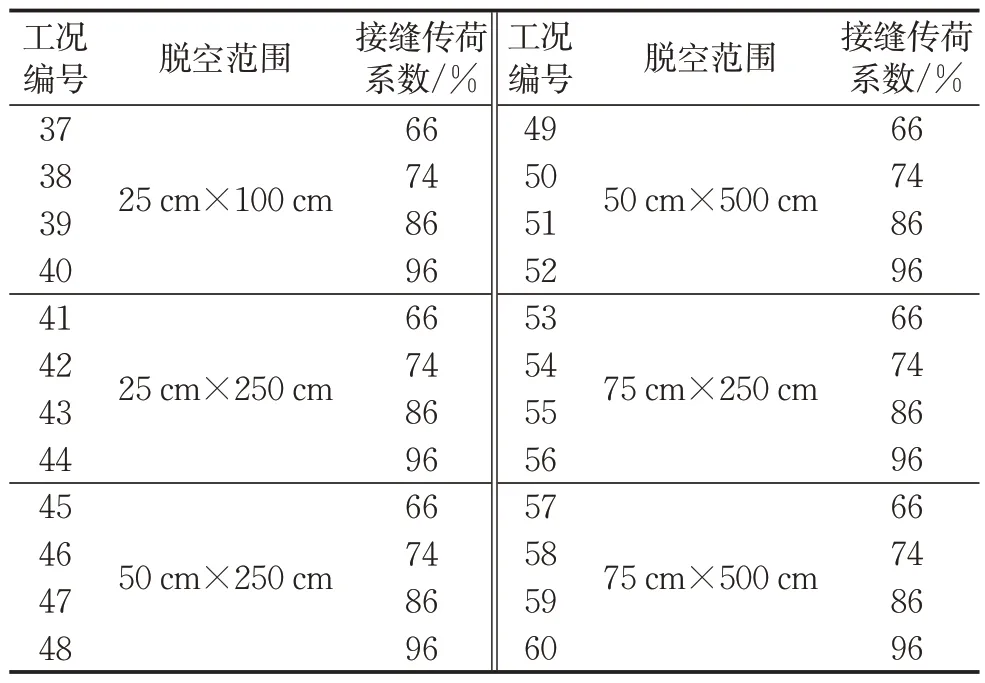
表5 有限元分析工况（板边脱空）Tab.5 Scenarios of finite element analysis (supportloss in edge)

图5b 为INP 文件生成步骤。读取原始INP 文件后依据各工况对应支承状态，寻找脱空区域对应单元编号，定义该单元层间接触弹簧刚度；依照荷载类型（A320、A330、A380）定义荷载形式及加载面；根据接缝传荷系数定义接缝处弹簧刚度。结构部件定义完成后，添加各分析步并定义对应的加载时间、步长及加载位置。最后，设置道面板的应变、变形数据输出，并调用Abaqus软件分析程序运行脚本。

2.3 板角脱空的影响

表6 为接缝传荷系数86%时不同机型、不同支承状态下板角脱空区内的最大弯拉应力及其位置。可以发现，当接缝传荷系数较高时，板角脱空对最大弯拉应力的大小、位置均无显著影响。随着板底脱空加剧，最大弯拉应力位置仍于荷载作用位置的板底。

表7 为接缝传荷系数66%时不同机型、不同支承状态下板角脱空区内的最大弯拉应力及其位置。可以发现，当脱空范围超过75 cm时，最大弯拉应力出现位置转移至脱空区边缘，在板厚方向上也由板底变为板顶。随着损失范围增大，最大弯拉应力也显著增大。这说明，接缝传荷系数降低后，板角支承对最大弯拉应力的影响逐渐显著。

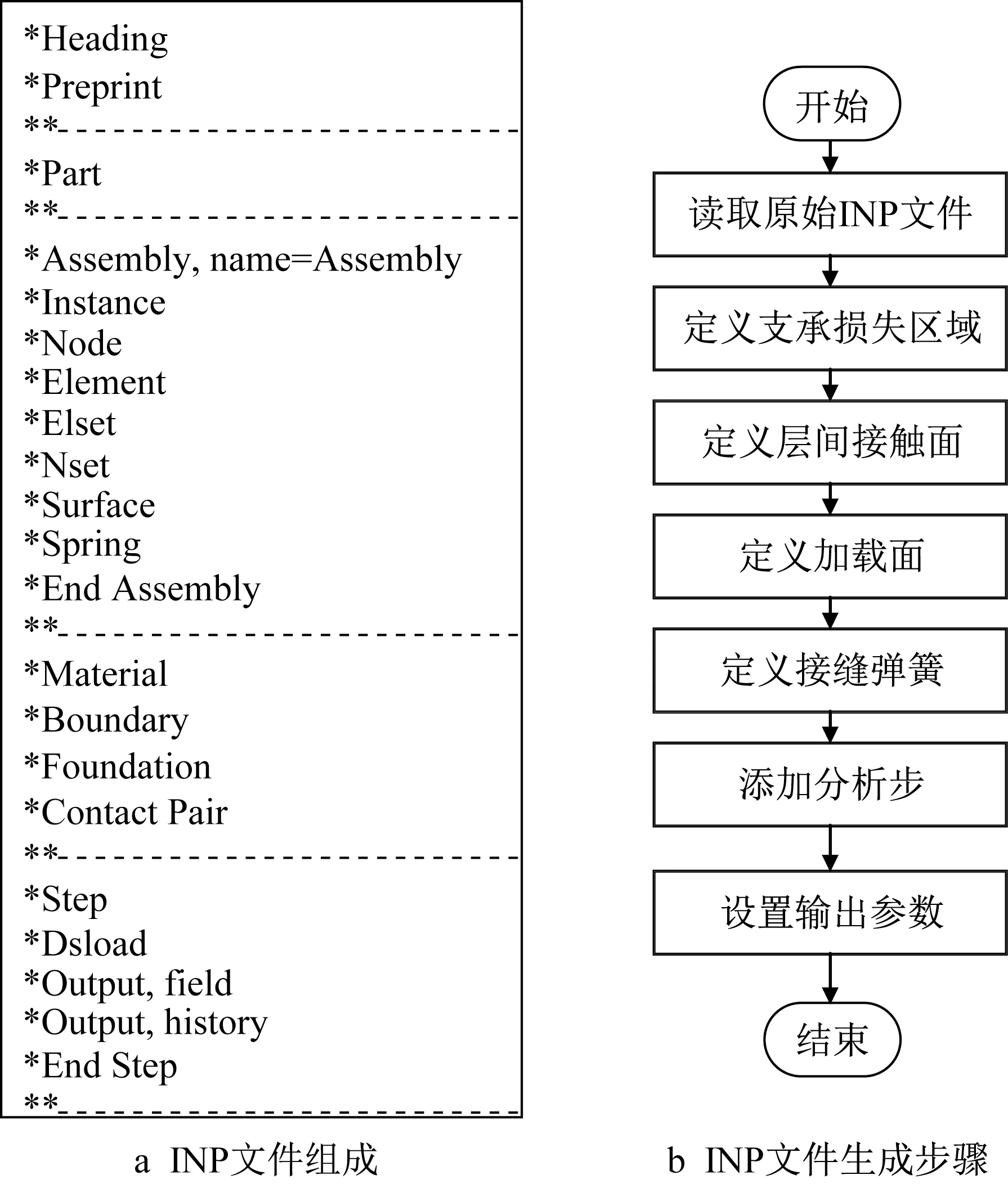
图5 模型计算过程Fig.5 Procedure of model calculation

为进一步分析板角脱空对弯拉应力分布的影响，分别计算在A320荷载作用下，25 cm脱空、75 cm脱空、150 cm 脱空对应的板底、板顶弯拉应力分布，如图6 所示。由图6a 可发现，25 cm 脱空时，最大弯拉应力出现在板底，并且位于荷载作用位置正下方。由图6b可发现，75 cm脱空时，最大弯拉应力位置从板底变为板顶，并且平面位置转移至脱空边缘处。此外，由图6c可发现，150 cm脱空时，最大弯拉应力已经超过5 MPa，大于混凝土弯拉强度，极可能导致道面板发生断裂破坏。综上，板角脱空范围扩大后，板内应力分布发生明显变化。脱空区域内板顶的弯拉应力逐渐增大，甚至超过板底的弯拉应力，并且最大弯拉应力的平面位置也由荷载正下方转移到脱空范围的边界上。原因在于，板角脱空后，损失范围内的道面板边界条件发生变化，逐渐退化为悬臂结构，对受力形态产生显著影响。

2.4 板边脱空的影响

表8 为接缝传荷系数66%时不同机型、不同支承状态下板边脱空区内的最大弯拉应力及其位置。与板角支承类似，随着板边脱空范围的增大，最大弯拉应力逐渐由荷载作用位置的板底转移至脱空区边缘的板顶，并且最大弯拉应力显著增大。该规律说明，与板角脱空类似，板边脱空也会对最大弯拉应力的平面位置及其板厚方向上的位置产生显著影响。

表6 板角脱空状态下最大弯拉应力（接缝传荷系数86%）Tab.6 Maximum load stress with support-loss in corner（86%load transfer coefficient）

表7 板角脱空状态下最大弯拉应力（接缝传荷系数66%）Tab.7 Maximum load stress with support-loss in corner（66%load transfer coefficient）

图7 为接缝传荷系数66%时板边脱空25 cm×250 cm、50 cm×250 cm 2 种工况对应的弯拉应力分布。由图7a可见，当脱空范围较小时，板角区域的最大弯拉应力出现在荷载作用处的板底；当脱空范围较大时，板顶区域的弯拉应力显著增加，并位于脱空区域边缘的板顶，如图7b所示。该现象进一步佐证了板边脱空对道面板应力分布的影响。

2.5 接缝传荷性能的影响

图6 板角脱空状态下弯拉应力分布Fig.6 Load stress distribution with support-loss in corner

表8 板边脱空状态下最大弯拉应力（接缝传荷系数66%）Tab.8 Maximum load stress with support-loss in edge（66%load transfer coefficient）

接缝传荷性能同样会影响道面板应力分布。图8a 为板角脱空75 cm 时，不同接缝传荷系数下各机型作用产生的最大弯拉应力及位置。可以发现，接缝传荷系数越高，脱空对最大弯拉应力的影响越小；当接缝传荷系数较低时，脱空的影响较为显著，导致最大弯拉应力显著增大，并且出现位置也由板底转移到板顶。由于不同机型的荷载大小存在区别（A330 ＞A380 ＞A320），在相同接缝传荷系数下A330 机型作用产生的最大弯拉应力显著大于其他机型，而A320机型对应的最大弯拉应力最小。上述3种机型中，接缝传荷系数对最大弯拉应力的影响规律一致且明显。

图8b为板边脱空50 cm×250 cm时接缝传荷系数对最大弯拉应力的影响。可以发现，板边脱空状态下接缝传荷系数的影响与板角脱空时的类似。接缝传荷系数越小，最大弯拉应力越大，并且最大弯拉应力的出现位置逐渐由板底转移到板顶。该影响规律在不同机型中显著且一致。

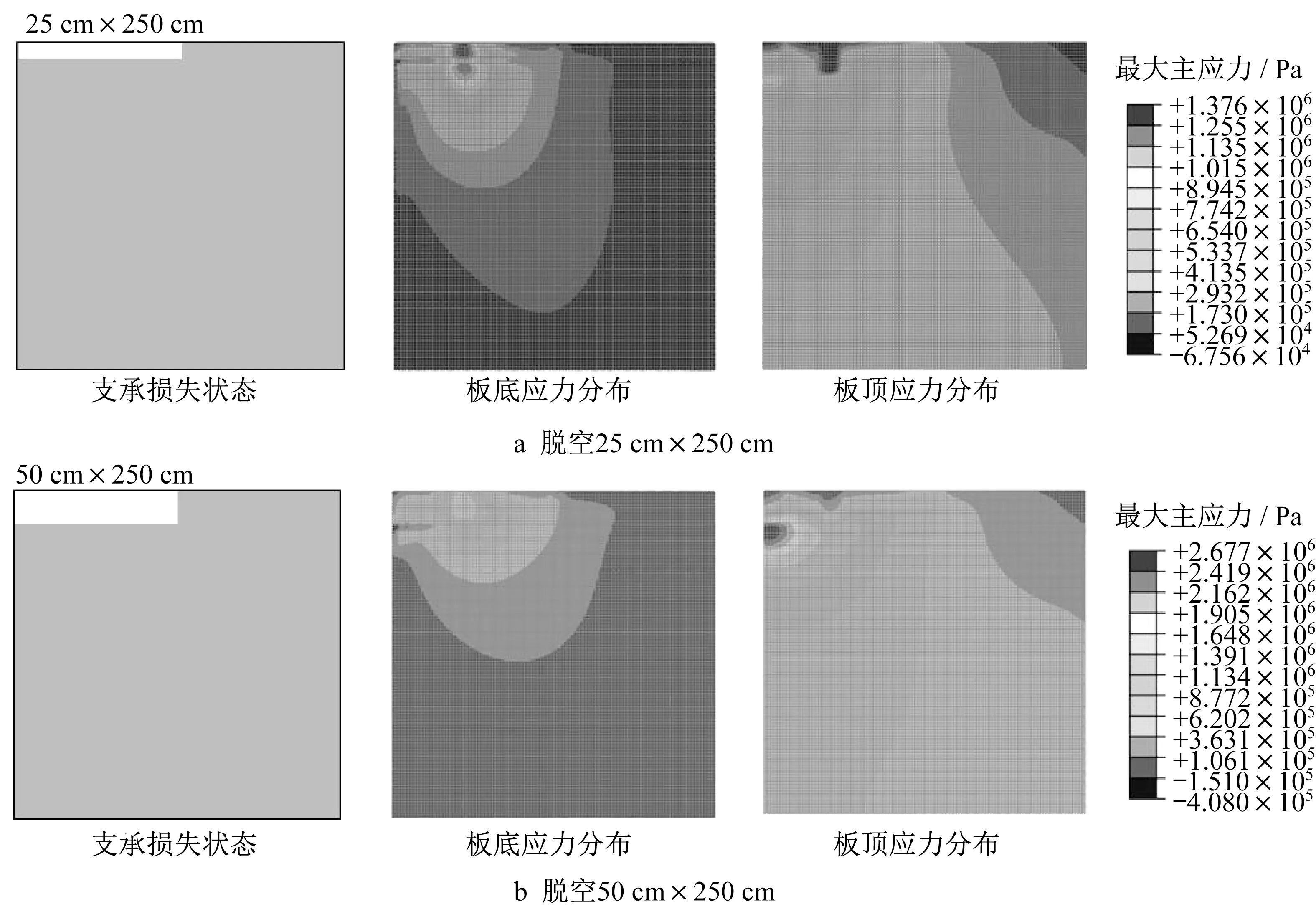
图7 板边脱空状态下弯拉应力分布Fig.7 Load stress distribution with support-loss in edge

图8 接缝传荷系数对最大弯拉应力的影响Fig.8 Effect of load transfer coefficient on maximum load stress

3 临界脱空状态

3.1 脱空评定方法

随着脱空发展，弯拉应力分布不断变化，最大弯拉应力也逐渐增大，极易诱发刚性道面板断裂。因此，亟需提出一种准确、便捷的脱空评定方法，以快速甄别板底脱空程度，避免道面结构破坏。鉴于我国现行机场水泥混凝土道面设计规范采用临界荷位下的弯拉应力，即以最大弯拉应力作为设计依据，因此本研究以健康状态（即无脱空）下刚性道面板临界荷位的最大拉应力（即荷载作用于纵缝中部的板底弯拉应力）为参考阈值。若脱空导致板内最大拉应力超过该参考阈值，则表明该板受力状态已不符合设计要求，其剩余使用寿命将受显著影响，需及时开展养护维修，因此以此时脱空状态为临界脱空状态。

为探究飞机荷载类型、接缝传荷系数对刚性道面板临界脱空状态的影响，依托构建的道面板数值仿真模型，重点考虑实际工程中常见的板角脱空，分别计算不同机型、接缝传荷系数下板角脱空区内最大弯拉应力随脱空范围的变化情况，并与参考阈值相互对比。从图9a可以发现，接缝传荷系数为66%时，在脱空前期，损失区内的最大弯拉应力小于参考阈值，说明此时脱空对道面板应力分布影响有限，板内最大弯拉应力依旧为设计阶段临界荷位（纵缝中部）的板底弯拉应力；当脱空发展至75 cm 左右，损失区内的最大弯拉应力超过参考阈值，表示该支承状态下道面板临界荷位发生变化，已不符合设计要求。因此，可认定该算例中3 种机型作用下刚性道面板临界脱空状态对应范围为75 cm。从图9b可以发现，接缝传荷系数提升至74%后，2条曲线的交点轻微向右偏移，说明临界脱空状态对应范围有所增加（约为78 cm），而且3种机型对应的临界脱空状态相近，未见明显差异。上述现象表明，飞机荷载类型对刚性道面板临界脱空状态无显著影响，但接缝传荷系数会影响刚性道面板临界脱空状态，接缝传荷系数越低，临界脱空状态对应范围越小。

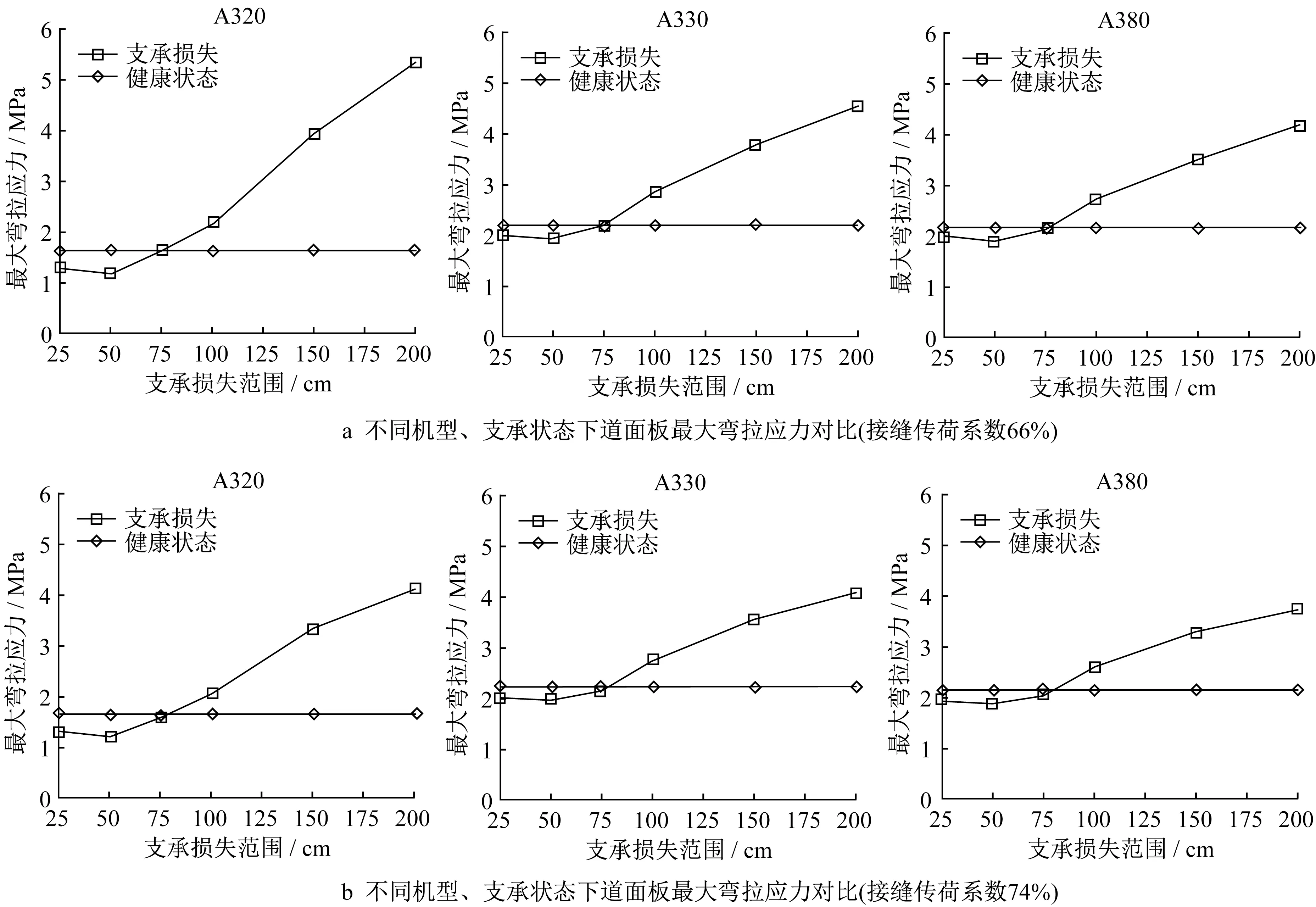
图9 临界脱空状态Fig.9 Critical support condition

3.2 与现有评定指标对比

现有的刚性道面支承状态评价指标包括《民用机场道面评价管理技术规范》（MH-T 5024―2009）中选用的弯沉比法和美国联邦航空管理局（FAA）采用的截距法。弯沉比法通过计算“测点弯沉/板中弯沉”以判定是否存在板底脱空。截距法则通过测量不同荷载级位作用下的弯沉值，采用线性回归的方式获得荷载和弯沉的相关关系，并通过拟合直线在弯沉坐标轴上的截距判定支承状态。为了研究上述2 种方法与临界脱空状态的关系，利用构建的道面板模型、冲击荷载模型，重点考虑常见的板角脱空形式，分别计算在不同支承状态、不同接缝传荷系数下的弯沉比指标与截距指标，如图10所示。

（1）弯沉比法

图10a为不同板角脱空、接缝传荷系数下的弯沉比。可以发现，板角脱空出现后，板角弯沉比逐渐增加，并且接缝传荷系数越低，弯沉比增幅越大。同时，即使支承状态相同，不同接缝传荷系数下的道面板弯沉也差异显著，说明接缝传荷系数对道面板弯沉具有显著影响。此外，《民用机场道面评价管理技术规范》中板角弯沉比指标的判定阈值是3.0，图10a中不同接缝传荷系数下，脱空75 cm 对应的弯沉比均小于3.0，表明道面板在达到弯沉比指标阈值前已处于临界脱空状态，道面板结构的受力状态已受到明显影响。

（2）截距法

图10b为不同接缝传荷系数下，板角脱空75 cm对应的截距指标。荷载级位依据冲击荷载模型，分别为100 kN和140 kN。可以发现，在不同接缝传荷系数下，临界脱空状态对应的截距指标差异不大（41～48 μm），但均小于FAA的脱空判定阈值76 μm的判定标准。上述现象表明，在达到截距指标阈值前，刚性道面板已处于临界脱空状态。

综上所述，弯沉比指标、截距指标虽然能在一定程度上反映道面板支承状态，但是由于其阈值选取主要依据现场测试经验，并且测试结果容易受到接缝传荷性能以及环境因素的干扰，导致在达到指标阈值前刚性道面板受力状态已经发生明显变化。相比之下，临界脱空状态能够更准确地反映脱空对刚性道面板应力分布的影响，具备评定板底脱空的潜力。

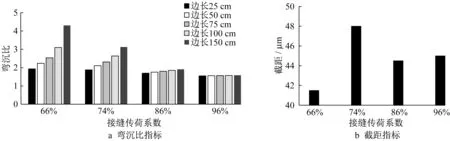
图10 临界脱空状态与弯沉指标对比Fig.10 Comparison of critical support condition and deflection-based indexes

4 结论

（1）层间弹簧单元可有效模拟刚性道面板支承状态，并可通过移除脱空区内的弹簧单元模拟板底脱空。与传统库伦摩擦模型对比后发现，两者在弯拉应力、竖向变形上的结果差异在5%以内，一定程度上验证该模型的准确性。同时，相较于库伦摩擦模型，弹簧模型可缩短95%的计算时间，并且具备易收敛的优势。

（2）板底脱空会影响道面板表面弯沉，并导致板内弯拉应力重分布。随着脱空加剧，表面弯沉及最大弯拉应力随之增大。当板角脱空达到边长75 cm、板边脱空达到50 cm×250 cm 时，道面板最大弯拉应力位置将发生改变，平面位置转移至脱空区边缘，板厚方向上也由板底转移至板顶。然而，板底脱空的影响程度与接缝传荷性能有关，接缝传荷性能越好，板底脱空对弯沉和弯拉应力的影响显著性就越低。

（3）当板底脱空范围达到一定程度时，荷载作用下道面板内的最大弯拉应力将超过健康状态下临界荷位对应的峰值应力，将此定义为临界脱空状态以评定脱空的影响，并通过构建的数值仿真模型将该评定方法与弯沉比法、截距法对比，结果显示临界脱空状态能够更准确地反映脱空对刚性道面板应力分布的影响，具备评定板底脱空的潜力。

作者贡献声明:

赵鸿铎：主要负责研究思路、构架与文稿撰写。

曾孟源：主要负责数据处理与部分文稿撰写。

吴荻非：主要负责有限元建模与文稿撰写。

凌建明：主要负责研究方法与实施方案。

韦福禄：主要负责足尺试验。