城市地下互通立交通行能力计算

（上海市政工程设计研究总院（集团）有限公司，上海 200092）

城市地下互通立交在物理环境和交通环境等方面不同于地上道路，具有以下特点［1-2］：物理环境方面，地下空间封闭，缺少自然光，影响驾驶员判断，噪声导致注意力下降，能见度低，驾驶员反应时间加长；交通环境方面，视距不足，驾驶员心理上会拉大安全距离。这些特点决定了地下互通立交与地上道路通行能力的差异。李文权等［3］通过可接受间隙理论等方法研究了互通立交通行能力，但与交通实测值吻合性有待进一步验证，并且未考虑地上与地下道路的差别。李素艳［4］归纳了地下道路交通流特性，并给出跟车车头时距值，从而得到地下道路主线通行能力，但计算时假设前后车的刹车行驶距离相同，与实际情况存在一定偏差，而且未针对地下互通立交进行分析。美国交通研究委员会出版的《道路通行能力手册》［5］，系统地论述了各种类型、型式的道路通行能力，包括道路主线、匝道分合流区、交织区等，但计算参数仅适用于美国实情，也未针对地下道路及地下互通立交提出专门的分析方法。Westphal［6］基于互通式立交合流区车流运行的实际调查，分析了速度和流量，建立了合流区通行能力模型，但是该模型的标定是根据德国快速路的经验调查，未涉及地下道路。Kim等［7］在可接受间隙理论的基础上，考虑主线车头时距服从Erlang分布，得出合流区通行能力计算模型，但是该模型在主线流量较大时是否适用仍待进一步验证，同时也只考虑了地上道路的情况。鉴于目前国内外对于城市地下互通立交通行能力尚未形成明确的计算方法，现有规范中也无相关明确规定，因此深入研究城市地下互通立交通行能力很有必要。从车道通行能力机理出发，分别对城市地下互通立交主线路段、匝道路段、匝道合流区、匝道分流区等通行能力的计算方法进行研究，通过实测验证并给出推荐值，为城市地下互通立交设计提供重要依据。

1 地下互通立交主线路段通行能力

车道基本通行能力指一条车道的最大通行能力（不特别说明，以下简称通行能力），通常有3种研究方法，即理论分析法、仿真法和实测法。传统的理论分析法以车头间距为研究对象，仅考虑前车瞬间静止的状况，导致理论计算小于实际情况；部分研究者采用仿真法来确定车道通行能力；我国相关规范中通行能力取值采用的是实测法。下面将从交通驾驶行为出发，深入研究车头时距理论模型，并结合地下互通立交特点，分析各参数取值，给出地下互通立交主线路段通行能力的推荐值。

1.1 基于期望车头时距的理论模型

根据通行能力的定义，通行能力是前后车辆保持最小车头间距情况下产生的。传统理论认为，采用前车瞬间停止时的最小车头时距进行计算，而实际情况下运行中的前车不可能瞬间停止，驾驶员跟驰心态为在保证安全距离的基础上尽可能靠近前车行驶，即交通流运行基于驾驶员期望车头时距。车辆跟驰模型运用了动力学方法，表达了车辆在排队行驶中后车跟随前车的状态。车辆跟驰模型最早由Reuschel 和Pipes 于20 世纪50 年代提出，随后国内外学者对车辆跟驰模型进行了大量研究［8-9］。较为常用的是基于考虑驾驶员反应延迟的线性跟驰模型［10］，但是后车的加速度与车辆间距无关，仅为其与前车相对速度的函数，与现实情况不符。随后其他学者提出了诸多改进模型。Gazis 等采用由灵敏度系数与车头间距成反比关系得到的非线性跟驰模型［11］和基于此推广的通用汽车（GM）模型［12］。当前研究仍然普遍基于20世纪60年代提出的模型，因此需要结合现代情况对模型进行修正。根据跟驰理论相关研究［3］，结合实际安全驾驶行为以及实测数据（上海市交通信息中心提供的内环高架、上中路隧道、翔殷路隧道、大连路隧道、外滩隧道视频数据）、事故调查，通常情况下后车遇紧急情况的减速会分两阶段进行。第一阶段，后车判断出前车明显减速的情况下，尽快制动的同时考虑安全性不踩死刹车；第二阶段，在后车减至一定速度时，如判断出前车确实是紧急制动，则踩死刹车以最大程度紧急制动。因此，提出和实际交通运行更加吻合的跟驰理论模型，即连续车队采用以期望车头时距跟车的模式行驶，前车n和后车（n+1）的最小期望车头时距控制根据两阶段减速后保持的车距确定，如图1所示。

图1 分阶段制动位置关系Fig.1 Position relation based on staged braking

第一阶段后车一般制动，由正常行驶速度v降至相对安全的速度v′，减速度为a1；第二阶段紧急制动，减速至零，减速度同前车紧急制动减速度a0。通行能力q的计算式如下所示：

式中：L0为前后车初始距离；L反1为后车第一阶段制动反应时间下的行驶距离；L后制1为后车第一阶段减速制动后的行驶距离；L后制2为后车第二阶段紧急制动后的行驶距离；L前制1为前车第一阶段的行驶距离；L前制2为前车第二阶段的行驶距离；L安1为第一阶段制动后前后车需控制的安全距离；L安为前后车制动停止后的最小安全距离；L车为车辆平均长度；t为从制动需求至制动启动所经过的固定时间。

根据实测数据（调查统计了G60上海入城段（设计速度100 km·h-1）、内环高架（设计速度80 km·h-1）、大连路隧道（设计速度60 km·h-1）、外滩隧道（设计速度40 km·h-1）、龙腾大道（设计速度30 km·h-1）车辆减速数据），第一阶段减速度与设计速度成反比（一方面原因是高速运行的车辆在第一阶段判断时间内减速度与初始速度比值小；另一方面因为高速运行环境下车辆速度波动小，后车减速预期小），第一阶段降速比例m与设计速度v0的关系如表1所示。第一阶段末速度v′的计算式为

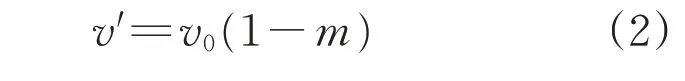
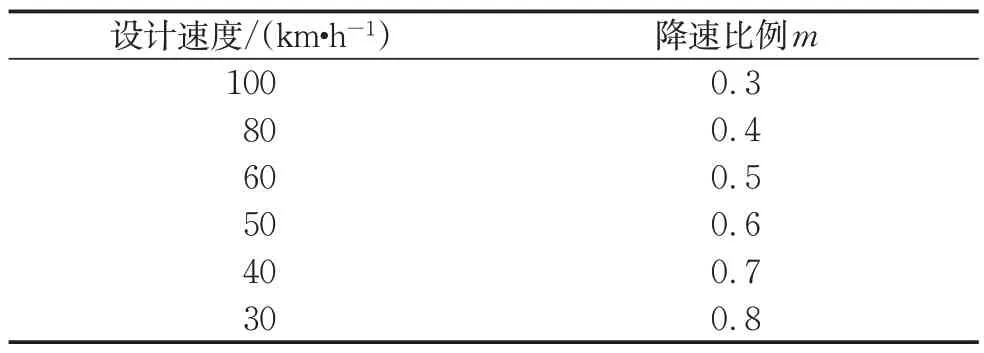
表1 第一阶段降速比例与设计速度关系Tab.1 Relationship between reduction ratio and design speed

1.2 理论模型的计算与验证

参考关于地上道路的行驶特性研究成果［13-14］，前后车辆安全距离L安=1.5 m，标准车辆长度L车=5.0 m，从制动需求至制动启动所经过的固定时间t=0.8 s（包含反应时间、抬脚时间、踏下时间、制动起作用时间）。根据实测数据调研及相关研究［15-16］，第一阶段后车尽快制动的同时考虑安全性不踩死刹车，减速度a1=4.0～5.0 m·s-2，设计速度高于60 km·h-1时取5.0 m·s-2，设计速度60 km·h-1及以下时取4.0 m·s-2。对于前车紧急制动以及后车第二阶段确认紧急制动（刹车踩死）的最大减速度，车辆完全抱死时轮胎摩擦滑动减速度为0.8g，而目前车辆基本均有防抱死功能，根据对常规车辆的调研，一般车辆最大减速度可以达到约10 m·s-2，因此a0取10.0 m·s-2。

基于以上参数取值，按照式（1）分别求得地上道路在不同设计速度时的通行能力模型计算值，与规范值［17］（实测值）的比较如表2所示。

表2 城市地上道路通行能力取值对比Tab.2 Comparison of traffic capacity values for urban ground road

基于最小车头时距的通行能力模型计算所得结果与现行城市道路工程设计规范的规定值（实测值）基本一致，这也验证了所提出模型的科学性和适用性。

1.3 地下互通立交主线路段通行能力的计算

根据前述分析的城市地下互通立交的物理环境和交通环境特点，参考李素艳［4］的相关研究成果，按照式（1）分别给出地下互通立交主线通行能力计算的参数取值。在地下道路时司机反应时间t1相比在地上道路时增加约0.2 s，取1.0 s；前后车辆安全距离加大，L安=2.0 m；其余参数取值同地上道路。

基于以上参数取值，按照式（1）分别求得不同设计速度时地下互通立交主线路段通行能力模型的计算值，并取整。根据实测数据（统计了上中路隧道（设计速度80 km·h-1）、翔殷路隧道（设计速度80 km·h-1）、大连路隧道（设计速度60 km·h-1）、外滩隧道（设计速度40 km·h-1）以及外滩隧道（延安东路和长治路出入口）的匝道分流区和匝道合流区），标定Vissim软件中驾驶行为模型（Wiedemann99）参数：跟车状态阈值的绝对值（取0.35 m·s-1）、进入跟车状态的阈值（取8 s）、车速摆动的加速度（取0.25 m·s-2）、起步加速度（取3.50 m·s-2），其余参数与通行能力关系不大，取默认值。Vissim 软件仿真值和地上主线路段规范值如表3所示。

表3 城市地下互通立交主线路段通行能力取值Tab.3 Traffic capacity values of main road for urban underground interchange

可以看出，地下互通立交主线路段通行能力模型计算值与仿真值误差在3%以内；相比现行城市道路工程设计规范中通行能力（地上道路）的规定值，地下互通立交主线路段通行能力折减约8%～11%（速度越高折减越多）。

为验证上述模型计算的可靠性，搜集了上中路隧道（设计速度80 km·h-1）、翔殷路隧道（设计速度80 km·h-1）、大连路隧道（设计速度60 km·h-1）、外滩隧道（设计速度40～50 km·h-1）等监控视频数据。以连续小客车车流作为统计单元，在设计速度80 km·h-1、40 km·h-1条件下，运行速度和通行能力的关系如图2、3所示。

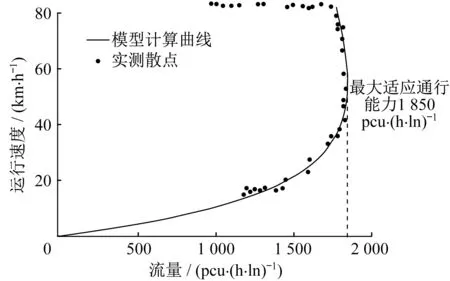
图2 运行速度与通行能力关系（设计速度80 km·h-1）Fig.2 Relationship between operating speed and traffic capacity（design speed 80 km·h-1）

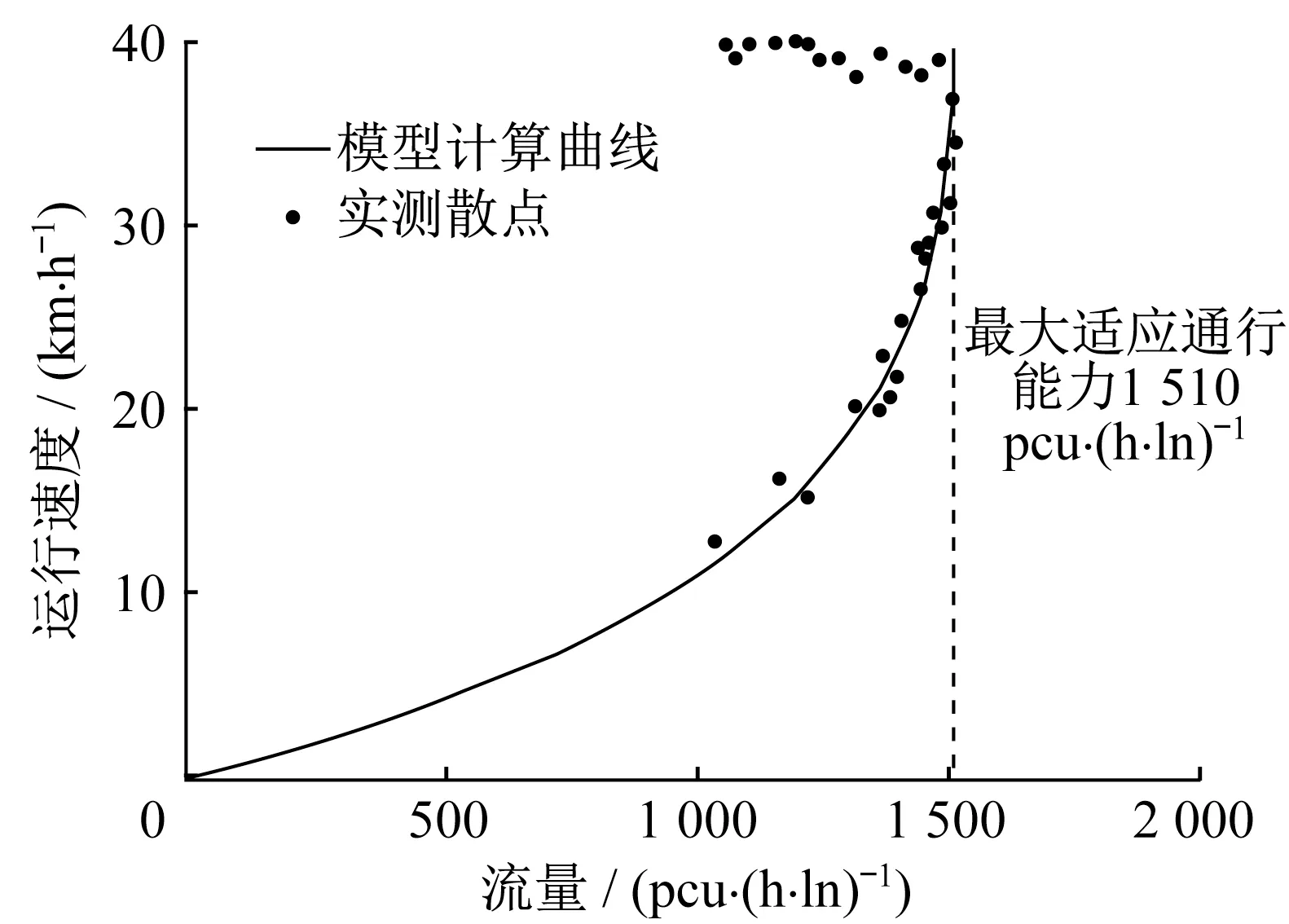
图3 运行速度与通行能力关系（设计速度40 km·h-1）Fig.3 Relationship between operating speed and traffic capacity（design speed 40 km·h-1）

当设计速度为80 km·h-1时，随着道路交通量的增加，运行速度从自由流速度开始降低，直至降低到约53 km·h-1时出现最大通行交通量1 830 pcu·h-1，与理论计算数据1 850 pcu·h-1基本吻合。图2还表明，服务交通量与运行速度成抛物线函数关系，即最大服务交通量出现在小于设计速度的某一运行速度。

当设计速度为40 km·h-1时，随着运行速度的增加，通行能力逐渐增加，约40 km·h-1时出现最大通行交通量1 520 pcu·h-1，与理论计算数据1 510 pcu·h-1基本吻合。图3 还表明，服务交通量与运行速度成单调增函数关系，即最大服务交通量出现在最大运行速度附近。

2 地下互通立交匝道路段通行能力

2.1 匝道路段通行能力影响因素

匝道是互通立交用来连接2条空间分离主线道路交通的单向行驶道路，匝道一般分为路段、分流区、合流区共3 个部分。车辆在匝道路段上运行主要受匝道本身的几何线形和特定驾驶行为的影响。由于受用地、工程投资和行车视距的多重约束，匝道的平面曲线半径及纵坡的选择经常受到限制；对于驾驶行为而言，在地下密闭空间中弯道行驶时，行驶视距比地上道路明显小，操作难度加大，往往采用加大前后车安全间距来保证行驶安全。因此，地下互通立交匝道的最小车头时距取值比地上立交匝道要大一些。

2.2 匝道路段通行能力确定

匝道路段通行能力仍采用前文所述期望最小车头时距模型。参数取值时根据实际地下互通立交匝道观测数据，前后车辆安全距离L安=3.0 m，其余参数同地下互通立交主线路段。按照式（1）分别计算并取整，得到不同设计速度下地下匝道路段通行能力计算值和Vissim 软件仿真值、地上匝道路段规范值，如表4所示。

表4 匝道路段通行能力取值Tab.4 Traffic capacity values of ramp section

可以看出，地下立交匝道路段通行能力模型计算值与仿真值误差在3%以内。相比现行城市道路交叉口设计规范中地上匝道路段的规定值，地下立交匝道路段通行能力计算值折减约14%，相比地下互通立交主线路段，地下匝道路段通行能力计算值折减约4%。

3 地下互通立交匝道合流区通行能力

3.1 匝道合流区通行能力含义

从匝道进来的车辆试着在相邻主线车道上寻找主线交通流中可利用空隙以便汇入，为保证交通安全，通常最外侧车道标线采用实线，则合流直接影响最外侧车道及加速车道。受合流车辆的影响，主线中车辆将在进口匝道上游重新分布，影响区域为主线所有车道及加速车道共同构成的合流区。合流区内侧车道不直接受进口匝道汇入的影响，其流量不超过车道设计通行能力。因此，匝道合流区通行能力分析的对象为合流影响区通行能力，即主线外侧车道交通量及匝道汇入合流区的最大交通量之和。

合流区通行能力受主线与匝道设计速度、主线与匝道流量比例、前后出入口距离、是否设置辅助车道、车辆汇入的临界间隙、车辆加速行为等影响。借鉴李文权等［3］关于地上互通立交合流区通行能力相关研究，针对地下互通立交匝道合流区的交通特点，在大量调查数据分析的基础上，运用回归分析法拟合出外侧车道流量计算公式，并给出地下互通立交合流影响区通行能力推荐值。

3.2 匝道合流区通行能力计算

根据地下道路设计规范［18］的相关规定，不同于地上立交，匝道接入主线入口处需要设置与主线平行的车道隔离段Lg（1倍的主线停车视距长度）；为了减少匝道汇入对主线的影响及主线内侧车道对匝道汇入的影响，在最外侧车道交织范围设置实线（即不允许主线内侧车道汇出至最外侧车道，也不允许外侧车道汇入至内侧车道）。如图4所示，匝道合流影响区流量为匝道流量VR与最外侧车道流量V1之和。

图4 地下互通立交匝道合流区示意图Fig.4 Diagram of ramp merge area for underground interchange

采用Vissim软件模拟主线双向六车道地下互通立交合流区车辆运行规律。驾驶行为参数选取前文标定的数值，加速车道、渐变段长度选取规范值［18］。假定前后出入口足够远并且不影响合流区，驶入匝道采用单车道，不设置辅助车道；立交匝道设计速度选择常用的40 km·h-1。对主线设计速度为60、80、100 km·h-1，不同主线流量、匝道流量情况下共100组样本数据进行仿真。通过统计产品与服务解决方案软件SPSS 给出外侧车道流量占主线上游流量的比例P1与匝道流量VR的关系，如下所示：

式中：vd为主线设计速度；VF为上游主线流量。按照式（3）计算外侧车道流量，按照式（5）计算合流影响区流量Vi，得到Vi取最大值时合流影响区通行能力推荐值Ci，如表5所示。

从表5 看出，地下互通立交匝道合流影响区通行能力相比地上互通立交［5］约折减10%。据此，对于地下互通立交，在预测主线和匝道流量基础上，得到合流影响区流量Vi，并与最大通行能力推荐值Ci进行校验，保证Vi＜Ci。

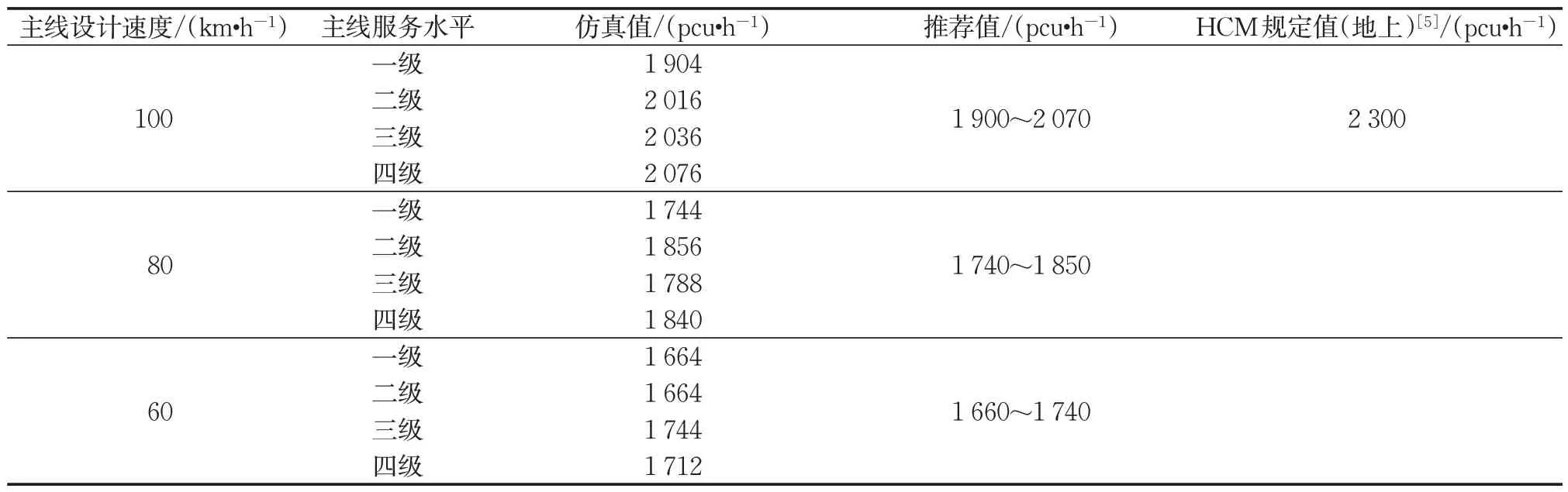
表5 地下互通立交匝道合流区通行能力推荐值Tab.5 Recommended traffic capacity values of ramp merge area for underground interchange

4 地下互通立交匝道分流区通行能力

4.1 匝道分流区通行能力含义

匝道分流区是指出口匝道上游到匝道分流点之间存在交织的一定范围内的所有车道区域。为了保证交通安全，通常最外侧车道标线采用虚实线以隔开主线内侧车道，则分流区通行能力分析对象为分流直接影响区域，即主线外侧车道以及减速车道区域。

分流区通行能力受主线和匝道的设计速度、主线与匝道流量比例、前后出入口距离、车辆减速行为等影响。借鉴李文权等［3］关于地上互通立交分流区通行能力相关研究，针对地下互通立交匝道分流区的交通特点，在大量调查数据分析的基础上，运用回归分析法拟合出外侧车道流量计算公式，提出地下立交分流影响区通行能力推荐值。

4.2 匝道分流区通行能力计算

对于地下互通立交，为减少分流对主线的影响，在最外侧车道分流范围设置实线（禁止内侧车道与外侧车道间交织）。图5 为地下互通立交匝道分流区示意图。如图5 所示，分流影响区流量即为最外侧流量V1（包含匝道流量VR）。

图5 地下互通立交匝道分流区示意图Fig.5 Diagram of ramp diverge area for underground interchange

采用Vissim软件模拟主线双向六车道地下立交分流区运行规律。驾驶行为参数选取前文标定的数值，减速车道、渐变段长度选取规范值［18］；假定前后出入口足够远并且不影响合流影响区，驶出匝道采用单车道；匝道设计速度选择常用的40 km·h-1。对主线设计速度60、80、100 km·h-1，不同主线流量、匝道流量情况下共100 组样本数据进行仿真，通过数据分析软件SPSS 拟合出外侧车道流量占主线上游流量的比例P1与匝道流量VR的关系，如下所示：

按照下式计算外侧车道流量：

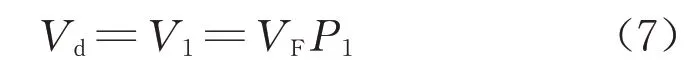
得到Vd取最大值时分流影响区通行能力推荐值Cd，如表6所示。分流影响区最大通行能力Cd发生在主线流量最大、匝道流量最大的情况下。从表6看出，地下互通分流影响区通行能力相比HCM 规定值［5］折减约11%。在预测主线、匝道流量的基础上，可计算出分流影响区流量Vd，并与Cd进行对照，据此可评判分流区服务水平情况。

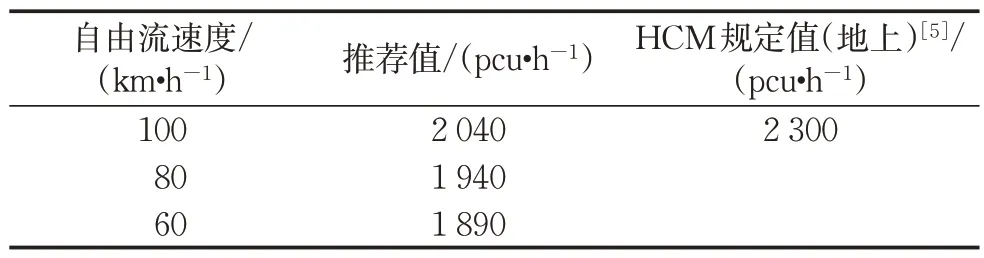
表6 地下互通立交匝道分流区通行能力推荐值Tab.6 Recommended traffic capacity values of ramp diverge area for underground interchange

5 结语

从车道通行能力机理出发，根据行驶车辆二次减速的实际情况，建立了基于期望车头时距的通行能力计算模型。结合城市地下互通立交物理环境和交通环境特点，提出了城市地下互通立交主线路段通行能力、匝道路段通行能力、匝道合流区及匝道分流区通行能力计算方法。结果表明，各部分通行能力均比地上互通立交通行能力有所折减，主线路段折减8%～11%（高速区间折减均接近10%），匝道路段折减约14%，匝道合流区折减约10%，匝道分流区折减约11%。下步研究可进一步扩充实测数据样本量，提高参数标定准确性。

作者贡献声明:

袁胜强：提出总体思路，部分章节撰写，全文统稿。

景 啸：模型构建，部分章节撰写。

史程祥：交通仿真及数值分析。