地铁杂散电流干扰下管地电位 波动特征的傅里叶分析

董亮，姚知林，葛彩刚，石超杰，陈金泽

（1.常州大学 江苏省油气储运技术重点实验室，江苏 常州 213164； 2.北京凯斯托普科技有限公司，北京 100028）

截至2019 年底，全球有167 个城市开通了地铁，轨道里程达15 622.61 km[1]。随着轨道交通的发展与地域条件的限制，在开通地铁的城市中已经出现了较多埋地管道与地铁轨道线路并行或交叉等邻近的情况，且这种案例的数量呈现增长的趋势[2-4]。在邻近地铁轨道的埋地管道上通常都会检测到杂散电流干扰，致使管道存在杂散电流腐蚀的风险[5-11]。国内外均出现过地铁工程投运后，其主体结构钢筋或附近钢质燃气管道发生多处腐蚀穿孔的情况[12-19]。

地铁杂散电流干扰下管地电位呈现不断变化的波动特征，针对其干扰特征国内外开展了一些研究。刘瑶等[20]对北京63 个不同程度与地铁交叉或平行的管道测试点进行管地电位测试，根据管地电位呈现出的周期波动规律对管地电位图像进行局部放大分析，统计出北京地铁杂散电流干扰引起的管地电位波动周期主要分布在50～200 s。朱祥剑等[21]对北京、上海、深圳、无锡等4 个城市地铁杂散电流干扰下的埋地管道的管地电位图像进行放大分析，经统计后发现同一城市不同测试点管地通电电位波动周期分布范围接近，不同城市的分布比例相差不大且均在0～300 s。刘杰等[22]对某处与地铁线路交叉的管道进行管地电位测试，同样对管地电位图像进行局部放大分析，发现地铁杂散电流的干扰周期可能与地铁实际运行工况有关。上述3 位研究者所采用的局部放大分析法由于需要人眼分辨并统计干扰波形的周期，这使得研究的工作量变得较为繁重，并可能会出现误差。王琼等[23]对距离铁轨3.5 m 的管道进行管地电位高频测试，对数据进行傅里叶变换后发现直流成分为–0.38 V，对应的交流成分频率约为50 Hz，幅值为2.68 V，即管道受到了电气化铁路交流杂散电流干扰。尽管该结果验证了傅里叶变换在实际操作中对管道杂散电流数据处理的有效性，但对于交流干扰而言同样可以测量交流管地电压进行判别。Chen 等[24]采用傅里叶变换对某测试点晚间时段30 min 的管地电位数据进行分析，同样采用观察的手段判断出测试点杂散电流的干扰频率范围为0～0.1 Hz，对管地电位中频率高于0.1 Hz 的波动进行过滤后，发现该段电位中有20 个波峰，同一时段内刚好有20 辆机车通过测试点，推测管地电位波峰的出现与机车通过测试点有关。而实际上，由于地铁轨道交通采用的是连通的焊接轨，即使没有机车通过测试点，只要轨道中有车辆在运行，管地电位就会出现干扰波动的情况。周宇等[25]以100 Hz 的频率采集了受轨道交通动态杂散电流干扰下的管地电位数据，并对21:10—21:20、22:00—22:10、00:00— 00:10 时段的数据进行傅里叶变换，通过观察发现管道所受杂散电流干扰的频率主要集中在0.5 Hz 以内，并据此判断轨道交通运行为主要干扰源，而对轨道交通运行与管地电位变化之间的规律未做深入研究。

针对地铁杂散电流干扰下管道的腐蚀，Qin 等[26]模拟了X70 钢在动态杂散电流干扰条件下的腐蚀行为，结果发现钢的腐蚀速率与干扰电流的周期有很强的相关性，随着干扰周期的增加，腐蚀速率逐渐增大直至稳定不变。为进一步研究地铁杂散电流干扰的频率范围和分布特征，并明确管地电位变化与地铁运行工况的相关性，本文采集了上海、广州、深圳、武汉等4 个不同城市内多个测试点连续超过24 h 的管地电位数据，采用快速傅里叶变换对夜间、早间、午间、晚间等多个时段的数据进行处理和统计分析，并结合地铁的实际运行工况得出地铁杂散电流干扰的一般特征规律。

1 傅里叶变换方法

在处理数字信号时，通常可将信号分析分为时域分析与频域分析，而傅里叶变换就是一种将信号从时域转换到频域的变换形式。傅里叶变换的基本原理是，任何连续测量的时序或信号都可以表示为不同频率的正弦波或余弦波信号的无限叠加。利用这一原理，可以快速分析出平稳或非平稳信号的频率特征，而地铁杂散电流干扰下波动的管地电位就是一种典型的非平稳信号。离散傅里叶变换是傅里叶变换最基本的方法并有着重要的作用，信号的频谱分析、滤波处理等都可以通过离散傅里叶变换来完成。离散傅里叶的运算公式为：

2 地铁杂散电流干扰下管地电位测试方法及数据基本特征

选取上海、广州、深圳、武汉等4 个城市中与地铁邻近且受干扰严重的埋地管道作为测试对象，采用 试片断电法测量管地电位，包括管地通电电位和断电电位，即在埋地管道阴极保护测试桩附近开挖测试坑，将极化试片与铜/饱和硫酸铜参比电极（CSE）一同埋设，将uDL2 数据记录仪的3 个接线端分别连接极化试片、参比电极和测试桩中埋地管道的引线。基于前文所述，已有研究结果表明地铁杂散电流干扰的频率范围为0～0.1 Hz 或处于0.5 Hz 以内[24,25]，而傅里叶变换可以处理得到采样频率一半以下的频率值，因此，设定采样频率为1 Hz，能够满足地铁杂散电流干扰频率分析要求。试片通断周期为通电12 s/断电3 s，通电和断电电位采集均为延时300 ms，连续测试24 h以上。测试连线示意图见图1。

图1 管地电位测试连接图 Fig.1 Schematic diagram of pipeline potential test

图2 为上海、广州、深圳、武汉测试点埋地管道24 h 电位图像，4 个城市测试点埋地管道的通电电位和断电电位均呈现白天波动大、夜间相对平稳的特征。由于断电电位更接近试片的极化电位，极化过程较慢且无IR 降的影响，各城市管地通电电位的波动均明显大于断电电位的波动。表1 为4 个城市管地电位数据及各测试点附近地铁运营时间的统计结果，由于在地铁运营前后需要进行空运巡线和维修检查工作，且地铁采用连通的焊接轨，每当有车辆在铁轨上运行时，就会出现杂散电流干扰，因此，各城市测试点的通电电位和断电电位出现明显波动的时间均早于附近地铁首班车发车时间，明显波动终止的时间均晚于末班车到站时间。由于运营起始和即将停运阶段的发车数量较少，首、末班车时段的管地电位波动小于白天其他时段的波动。

分别选取4 个城市晚高峰时段的管地通电电位进行局部放大，如图3 所示，可以发现管地通电电位上下波动具有一定的周期性，且幅值和频率随时间不断变化，显然是由多种不同的干扰波形叠加而成，而具体的干扰频率和幅值无法直接从时域数据中获取，后续利用快速傅里叶变换可对其进行变换分析。

图2 4 个城市测试点管地通电电位和断电电位图像 Fig.2 On-off potential of the test points in four cities: a) Shanghai, b) Guangzhou, c) Shenzhen, d) Wuhan

表1 4 个城市管地电位统计 Tab.1 Statistics of pipeline potential in four cities

3 地铁杂散电流干扰下管地电位的傅里叶变换分析

3.1 同一城市不同时段管地电位傅里叶变换分析

以上海1#测试点采集的数据为例，选取24 h、1:00—2:00、8:00—9:00、14:00—15:00 和17:00—18:00时段管地通电电位和断电电位数据，分别对应于全天、夜间停运及白天运行早、午、晚3 个时间段，采用ORIGIN 软件对数据分别进行快速傅里叶变换，变换结果如图4、图5 所示。

由图4a 可见，对管地24 h 通电电位进行快速傅里叶变换后，在多个频率处出现峰值点，这些峰值点中的最大幅值为9 mHz 处的172 mV。图4b 断电电位频谱图像中也在一些频率处出现峰值点，但由于断电电位波动并不大且采样的数据量较小，这些峰值点的幅值都相对较小且频率相对较大。由图5 可见，不同时段的管地电位在经过快速傅里叶变换后，通电电位频谱图像的波动明显大于断电电位频谱图像的波动，且夜间时段的通、断电电位频谱图像均波动不大，这与夜间实际的管地电位平稳特征吻合。通电电位频谱在早、午、晚3 个时段的最大幅值均出现在9 mHz位置，最大幅值分别为322、354、353 mV，均大于24 h 通电电位频谱中的最大幅值172 mV，因为傅里叶变换在对杂散电流信号进行分析时，信号分析结 果的平均值受该段信号的持续时长影响，管地电位白天波动大，夜间波动小，因此，全天24 h 管地电位频谱中的最大幅值要小于白天1 h 管地电位频谱中的最大幅值。

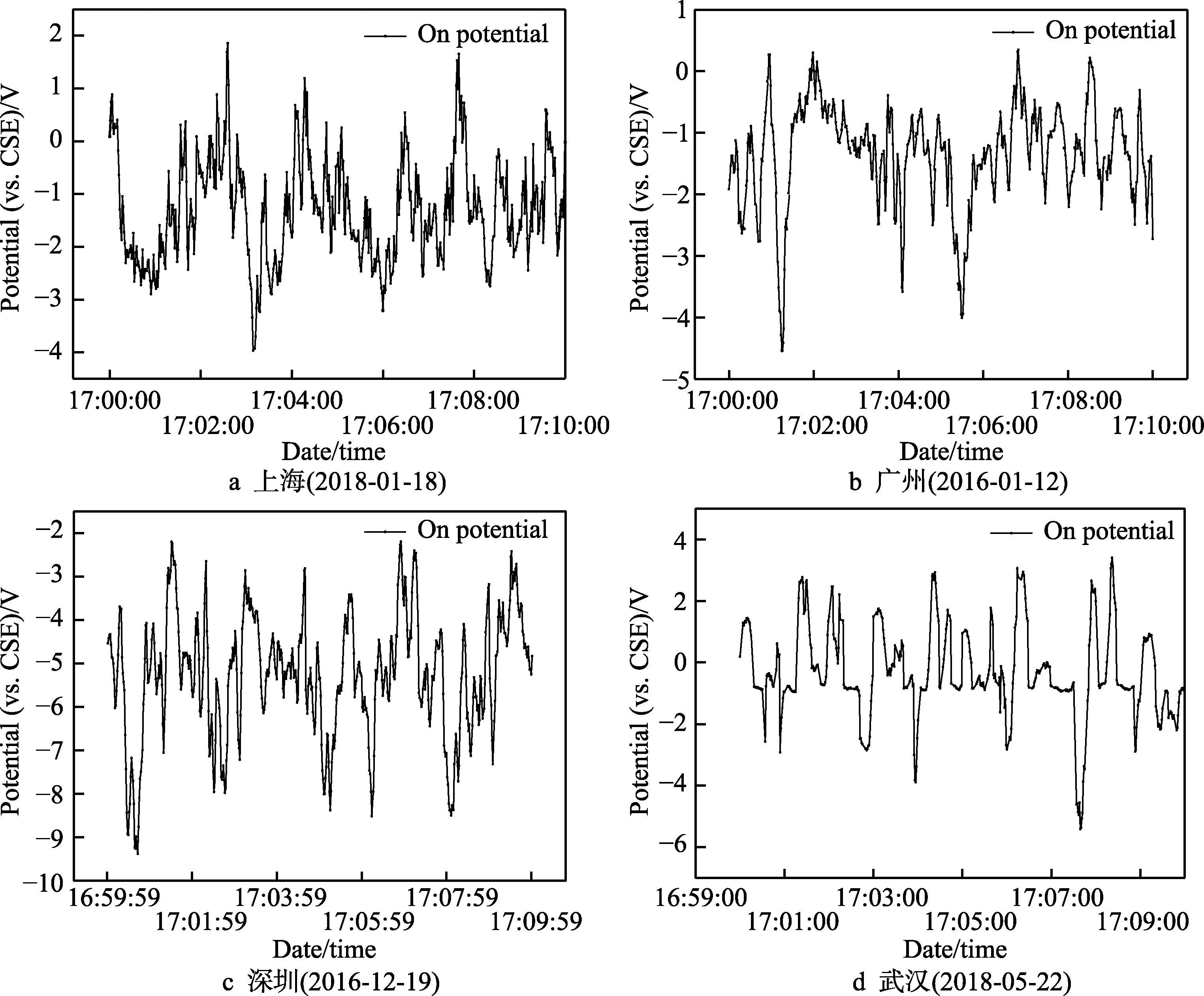
图3 4 个城市测试点17:00～17:10 管地通电电位图像 Fig.3 On potential from 17:00 to 17:10 of the test points in four cities: a) Shanghai, b) Guangzhou, c) Shenzhen, d) Wuhan

图4 上海1#测试点24 h 管地电位频谱图像 Fig.4 FFT spectrum of pipeline potential at Shanghai test point 1# in 24 h

图5 上海1#测试点1 h 管地电位频谱图像 Fig.5 FFT spectrum of pipeline potential at Shanghai test point 1# in 1 h

在对管地电位数据24 h 和每1 h 进行快速傅里叶变换后，进一步选取上海1#测试点17:00—18:00 与首、末班发车后各半小时内的通电电位数据，并对数据每10 min 进行1 次快速傅里叶变换，图6、图7 为变换后的频谱图像。其中首、末班发车后各半小时内的干扰最大幅值均小于17:00—18:00 时段的干扰最大幅值，这与首、末班车时段和白天其他时段的管地电位波动特征吻合。图中各时段干扰最大幅值对应的频率均为9 mHz，该结果与24 h 和每1 h 进行1 次快速傅里叶变换的结果一致。在后文中，将各时段分析结果中干扰最大幅值对应的频率称为干扰主频率，对应的周期称为干扰主周期。

图6 上海1#测试点17:00—18:00 每10 min 管地通电电位频谱图像 Fig.6 FFT spectrum of on potential every 10 min from 17:00 to 18:00 at the Shanghai test point 1#

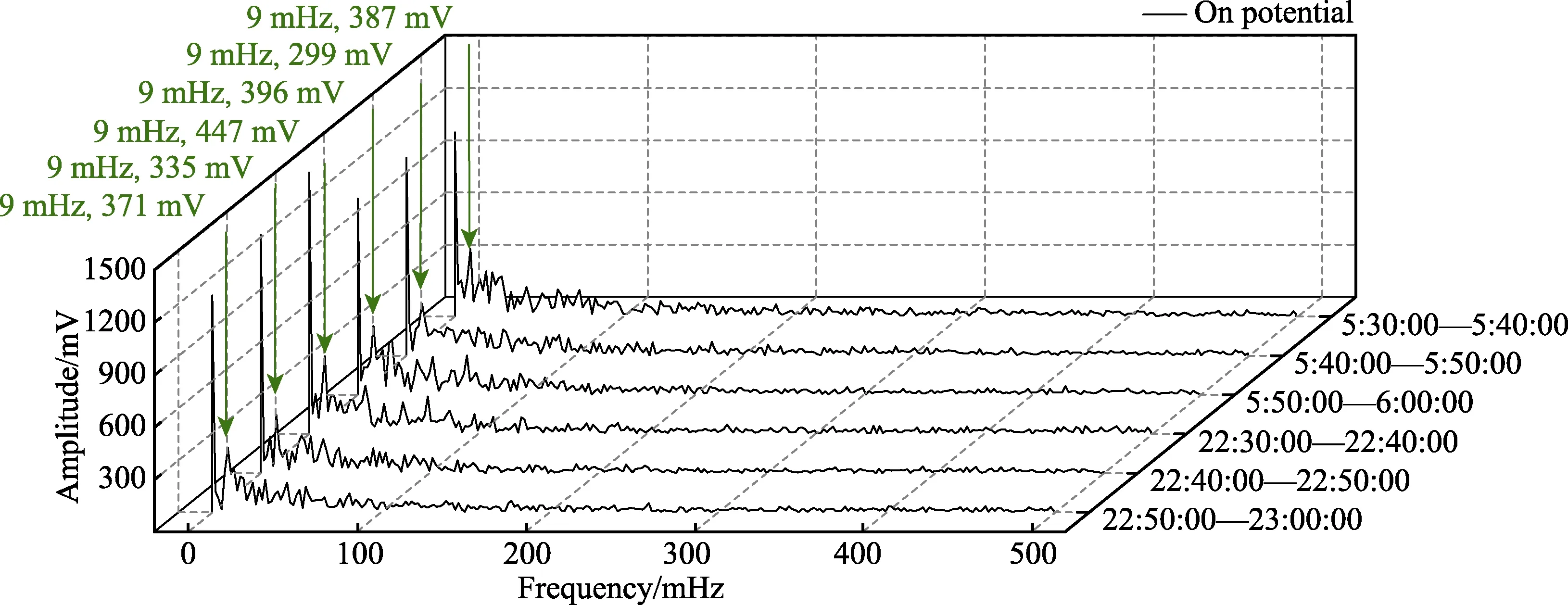
图7 上海1#测试点首、末班发车后每10 min 管地通电电位频谱图像 Fig.7 FFT spectrum of on potential every 10min from 5:30 to 6:00 and 22:30 to 23:00 at Shanghai test point 1#

为验证同一管道上受不同地铁线路影响的测试点管地电位波动是否具有相同的规律，选择该管线上受另一地铁线路影响的2#测试点采集的数据，对1:00—2:00、8:00—9:00、14:00—15:00、17:00—18:00 时段管地通电电位数据分别进行快速傅里叶变换，变换结果见图8。该测试点的通电电位数据分析结果同1#测试点的数据分析结果呈现相同的规律，除夜间没有明显波动外，其他时段均有明显的峰值点，其中幅值较大的峰值点集中在低频区域。各时段干扰的最大幅值分别为315、339、337 mV，与1#测试点各时段干扰的最大幅值接近，且这些幅值均出现在同一频率处，即各时段的干扰主频率相同。

为分析地铁杂散电流的频率范围及主要分布特征，选取上海1#测试点早、午、晚3 个时段频谱图像中幅值前10、前11～20、前21～50 以及幅值大于20 mV 的点统计见图9。图9 中可见3 个时段幅值前10点的周期集中在30～143 s，对应干扰频率为7～33 mHz；幅值前11～20 点的周期集中在23～163 s，对应干扰频率为6～44 mHz；前21～50 点的周期集中在15～187 s，对应干扰频率为5～67 mHz；幅值大于20 mV 点的周期范围为4～202 s，对应干扰频率为5～250 mHz。在地铁官网中调研上海1#测试点附近地铁线的站间等待时长，并除去地铁到站停留时间后统计出了地铁的站间行车间隔，发现该地铁线的站间行车间隔范围为30～150 s，主要站间行车间隔为120 s，这与1#测试点3 个时段幅值前10 点的周期范围和干扰主周期相近。图9 中幅值前10 点的幅值范围明显大于另外3 组的幅值范围，后文中将幅值前10 点的周期范围称为 该杂散电流干扰中占主导的干扰周期范围，对应的频率范围称为该杂散电流干扰中占主导的干扰频率范围。

图8 上海2#测试点1 h 管地通电电位频谱图像 Fig.8 FFT spectrum of on pipeline potential at Shanghai test point 2# in 1 h

图9 上海1#测试点管地通电电位频谱统计图 Fig.9 Statistic of on potential spectrum at Shanghai test point 1#

3.2 不同城市管地电位傅里叶变换分析

从广州、深圳、武汉3 个城市测试点的电位数据中同样选取1:00—2:00、8:00—9:00、14:00—15:00、17:00—18:00 等4 个时段数据，对这些数据分别进行快速傅里叶变换，图10—12 为变换后的频谱图像。3 个城市的通电电位频谱图像的波动都明显大于断 电电位频谱图像的波动，夜间时段通、断电电位频谱图像均波动不大。3 个城市的通电电位频谱图像中幅值较大的峰值点均集中在低频区，且早、午、晚3个时段的干扰主频率均为固定值，广州3 个时段的干扰主频率均为7 mHz，对应幅值分别为290、305、344 mV；深圳3 个时段的干扰主频率均为7 mHz，对应幅值分别为531、561、580 mV；武汉3 个时段的干扰主频率均为5 mHz，对应幅值分别为400、479、411 mV。

对上海及上述3 个城市早、午、晚时段通电电位频谱中干扰幅值前10 的峰值点进行特征统计，结果如表2 所示。4 个城市测试点地铁杂散电流干扰中占主导的干扰周期范围为27～250 s，对应的干扰频率为4～37 mHz。各城市间的干扰最大幅值有较大差异，其中深圳的干扰最大幅值明显大于其他3 个城市，可能有多种原因导致这一差异，包括供牵引变电站间距、牵引电流大小、轨道过渡电阻、土壤电阻率、管道和轨道相对位置等[27-28]。各城市间的干扰主频率也有所不同，广州和深圳的干扰主频率一致，上海测试点地铁杂散电流的干扰主频率要大于其他3 个城市，这可能与上海地铁交通更发达、站间行车间隔更短的原因有关，在后文中将进一步讨论。

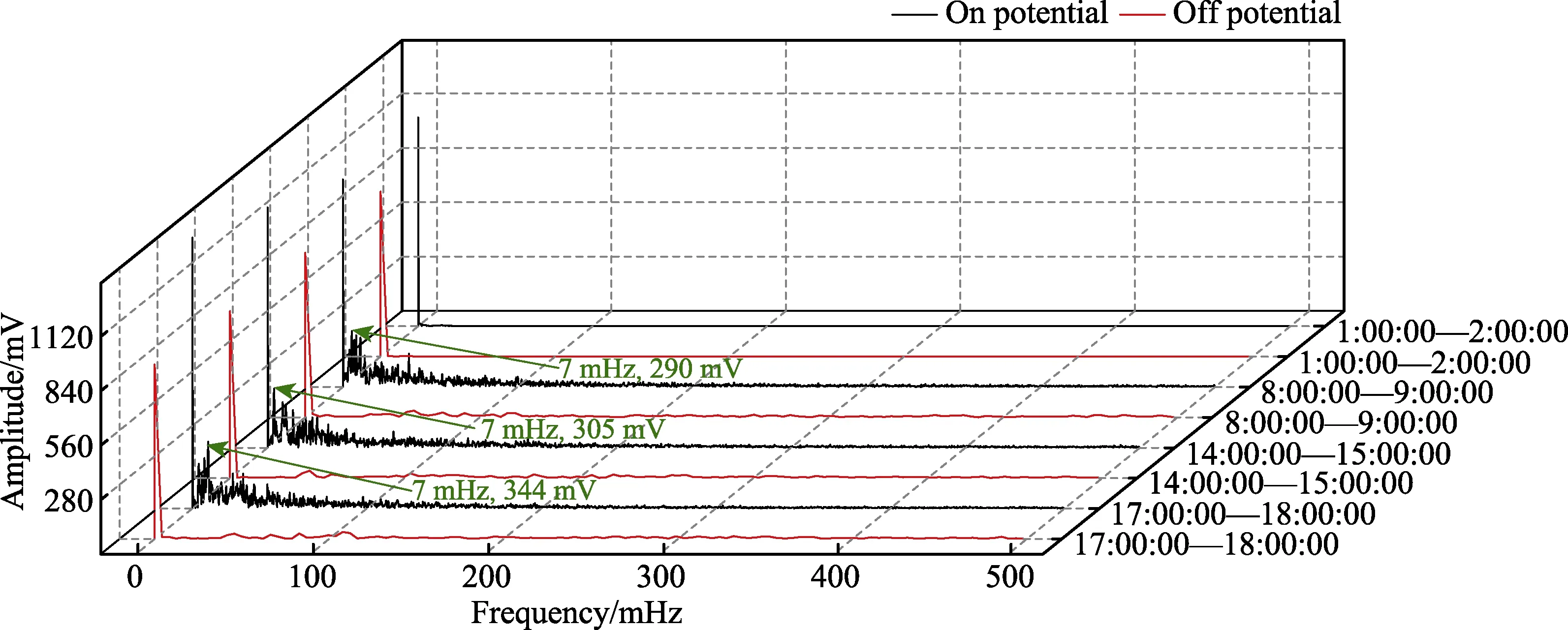
图10 广州测试点1 h 管地电位频谱图像 Fig.10 FFT spectrum of pipeline potential at Guangzhou test point in 1 h

图11 深圳测试点1 h 管地电位频谱图像 Fig.11 FFT spectrum of pipeline potential at Shenzhen test point in 1 h

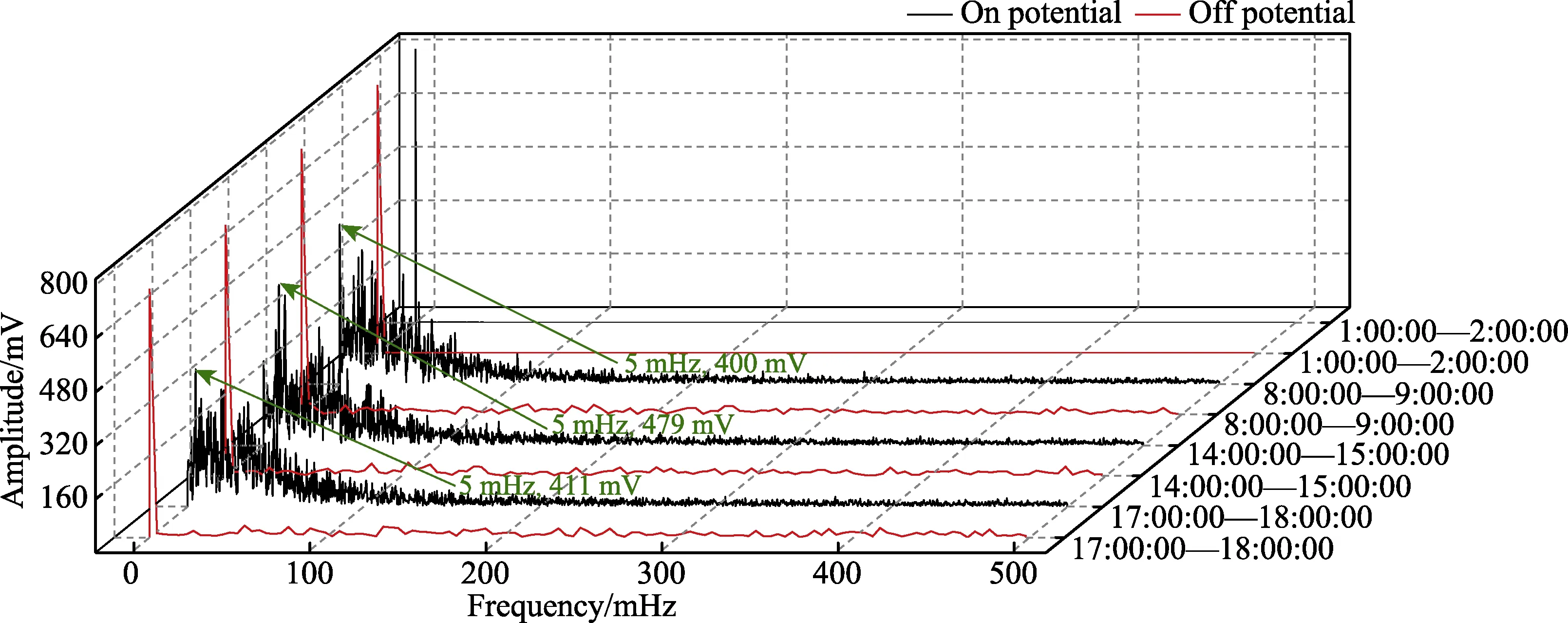
图12 武汉测试点1 h 管地电位频谱图像 Fig.12 FFT spectrum of pipeline potential at Wuhan test point in 1 h

表2 4 个城市测试点不同时段干扰特征数据 Tab.2 Interference characteristics of four cities test points at different times

3.3 管地电位波动特征与地铁运行工况对比

在各城市地铁官网中调研4 个城市测试点附近地铁的站间行车间隔，并对间隔时间进行占比统计，结果如图13 所示，在调研过程中，由于地铁系统提供的到站时刻表只能精确到半分钟，因此，理论站间行车间隔与实际站间行车间隔可能存在15 s 以内的误差。结合4 个城市管地电位快速傅里叶变换的分析结果统计如表3 所示。上海、广州、深圳、武汉地铁杂散电流干扰中占主导的干扰周期范围与地铁的站间行车间隔范围基本吻合。其中4 个城市测试点附近地铁的站间行车间隔分别以120、150、150、210 s为主，该结果与地铁杂散电流的干扰主周期基本吻合。由于轨道采用连通的焊接轨道，列车从上一站加 速启动至下一站减速停车时，管道测试点会受到一次完整周期的地铁杂散电流干扰，管地电位都会出现一个周期的波动，当一条地铁线中有多个站间行车间隔相同且有多辆列车运行时，与之对应周期的杂散电流干扰幅值就会叠加增大。地铁线的站间行车间隔决定了地铁杂散电流的干扰周期。

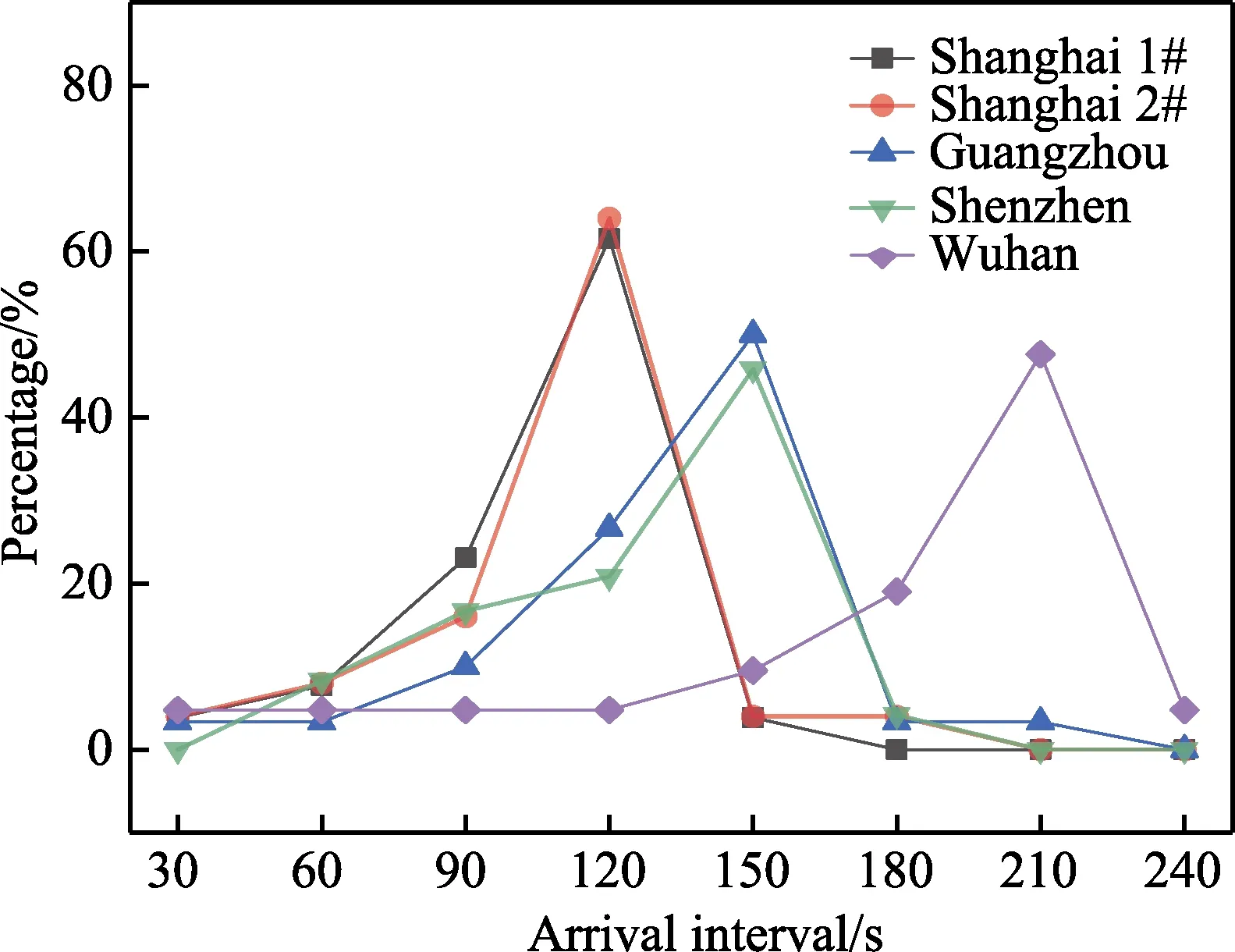
图13 4 个城市测试点附近地铁各站间行车间隔占比统计图 Fig.13 Statistics of driving interval between nearby metro stations in four cities

表3 快速傅里叶变换结果与测试点附近地铁线的实际工况统计 Tab.3 Results of fast Fourier transform and actual working condition of nearby metro

4 结论

1）由于断电电位极化过程较慢，使得响应速度较慢，而通电电位极化过程快，响应速度快且数据采集量大，因此，对通电电位进行傅里叶变换可以更好地体现出管道受地铁杂散电流干扰的特征。在对上海测试点管地电位进行快速傅里叶变换后，通电电位频谱图像除夜间外均有明显的波动，幅值大于20 mV的频率集中在5～250 mHz。同一测试点在干扰的不同时段内占主导的干扰频率范围接近，最大幅值对应的干扰主频率一致。

2）上海、广州、深圳、武汉测试点地铁杂散电流干扰中占主导的干扰频率范围分别为6～33、5～37、6～18、4～36 mHz，对应的周期范围与测试点附近地铁线的站间行车间隔范围吻合。各城市测试点地铁杂散电流的干扰主频率分别为9、7、7、5 mHz，对应的干扰主周期与测试点附近地铁线的主要站间行车间隔一致，地铁线的站间行车间隔决定了地铁杂散电流的干扰周期。

3）快速傅里叶变换分析可以有效地分析出地铁杂散电流的干扰频率范围及分布特征，结合附近地铁的实际运行工况可以辨识地铁杂散电流干扰的具体来源，同时可为管道防腐和实验研究的参数设定提供参考。