一种基于干扰观测器的永磁同步电机线性化反馈控制
2021-03-19陈施华游新望
朱 鹏,陈施华,张 杰,游新望
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
永磁同步电机具有高效、高功率密度、高可靠性的优点[1],广泛用于交流伺服控制系统中。针对永磁同步电机的跟踪控制,由于系统存在的非线性和外界干扰,传统控制具有一定的局限性,并且不能克服外界的干扰。[2]所以,针对永磁同步电机控制存在的问题,许多学者根据现代控制理论提出反步控制、滑模控制以及预测控制[3]等等。
本文提出的一种基于干扰观测器的线性化反馈控制,考虑到外界干扰的影响,在电机的数学模型中引入干扰项作为模型补偿。为了准确估计干扰项,设计了干扰观测器来实时估计干扰值。电机的控制策略采用线性化反馈的方法来实现,将系统的输出量与控制量构造线性微分的关系,然后利用线性控制方法构造控制器。
1 电机数学模型
根据永磁同步电机的工作原理,建立永磁同步电机在两相旋转dq坐标系下的数学模型,主要包括电压方程、磁链方程、转矩方程和运动方程。
(1) 电压方程
式中,uq、ud、iq、id、Lq、Ld分别为定子电压、电流和电感在q轴和d轴上的分量;Rs为定子绕组的电阻,ωr为转子的电角度,ψ为转子磁链。
(2) 磁链方程
式中,ψq、ψd分别为定子磁链在q轴和d轴上的分量。
(3) 转矩方程
(4) 运动方程
式中,ωm=ωr/np为电机机械角速度,J为转动惯量,B为粘性摩擦系数,Tl为负载转矩,np为极对数。
综合上述方程可得到永磁电机在旋转dq坐标系的数学模型为
对于表贴式永磁同步电机有L=Ld=Lq,采用id=0的控制方法,并考虑到建模误差和外部不确定干扰,引入干扰D,可将上述模型进行简化:
为了方便推导,将永磁电机的模型重新定义变量如下:
x1=ωm,x2=iq
可得模型为
在建立的永磁同步电机模型基础上,设计一种基于干扰观测器的线性化反馈控制,其控制原理框图如图1所示。参考速度信号为输入量,实际速度和q轴电流为反馈量以及外界干扰的观测值用来作为控制器的计算量,得到控制电压uq,进而实现电机的转速控制。
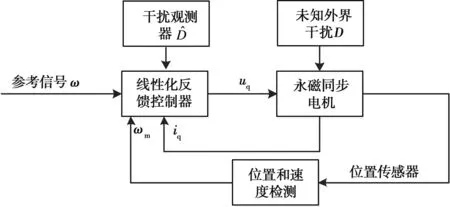
图1 系统控制原理框图
2 干扰观测器设计
干扰观测器是一种处理系统模型和外界扰动问题的有效控制手段,其主要思想是通过建立的名义模型和实际建立的系统模型作比较,将产生的误差输入到控制器的计算输入端,实现最终的干扰抑制补偿。干扰观测器已经能够很多好地与各种先进的控制算法结合应用,并取得了很好的控制效果。
为了消除系统的不确定干扰,设计一个干扰观测器用来对系统模型外的干扰进行观测。设计干扰观测器如下形式:
式中,p(x1,x2)为待设计的非线性函数,L(x1,x2)为非线性观测器的增益,两者满足如下关系:
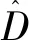

对等式两端进行微分,得
=L(x1,x2)(z+p(x1,x2))-
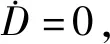
p(x1,x2)=bx2
3 线性化反馈设计
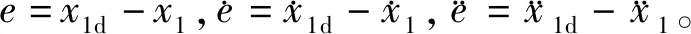
=a1θ1(-a2x2-a3ωm+a4uq+D)-θ2(a1θ1x2-θ2x1-θ3)
=a1θ1(-a2x2-a3ωm+D)-θ2(a1θ1x2-θ2x1-θ3)+
a1θ1a4uq
令
f(x,t)=a1θ1(-a2x2-a3ωm+D)-θ2(a1θ1x2-θ2x1-θ3)
g(x,t)=a1θ1a4
则
设计控制器为
其中,f,g为非线性函数,v为控制器的辅助项。设计v为
所以有
即
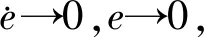
4 仿真结果
根据以上的公式推导,利用simulink搭建永磁同步电机模型和设计的控制器模型,仿真设定永磁同步的参数为:np=3,Rs=2.875 Ω,J=0.011 kg·m2,L=0.033H,B=0.002 N·m·s/rad,ψ=0.8 Wb。
为了验证控制策略的有效性,首先在构建的线性化反馈控制器上进行验证,参考输入信号为幅值为500的正弦信号,然后在建立的永磁电机模型基础上加入干扰D,最后在加入干扰的情况下将观测器的观测信号引入线性化反馈的控制当中。图2所示为程序控制反馈原理框图,主要包括信号发生器模块、控制算法模块、电机模型模块和干扰观测器模块。信号发生器模块主要用来生成参考的速度信号。控制算法模块用来将反馈的传感器信号进行计算,从而得到电机的控制信号。电机模型模块主要是上述在dq轴下建立的电机数学模型,包含了电压电流等方程。干扰观测器模块用来构造外界干扰的补偿项。
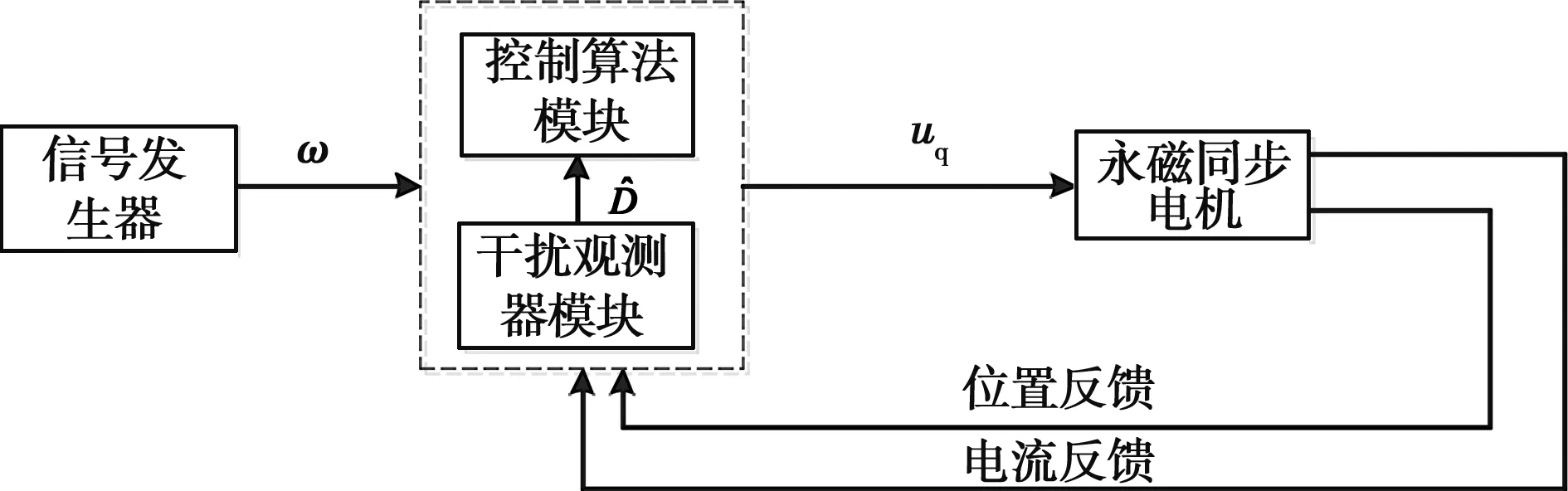
图2 控制反馈原理图
图3所示为在没有干扰的情况下输入参考信号和跟踪信号的曲线图。由图3可以看出,设计的线性化反馈控制器具有良好的跟踪控制性能。图4是在控制模型中引入了正弦干扰信号,可见跟踪的正弦信号出现了明显的波动。当加入了观测器的补偿项之后,由图5可见,跟踪曲线再次趋于平滑。

图3 无干扰下电机转速跟踪图
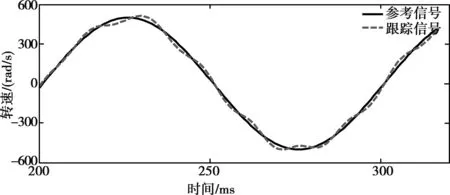
图4 有干扰下电机转速跟踪图
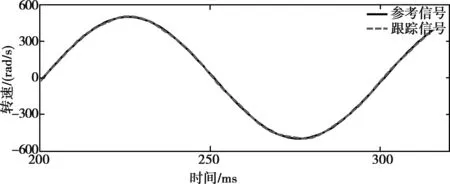
图5 有观测器下电机转速跟踪图
为了更好地观察跟踪效果,可以从图6的转速误差变化图中看到在没有干扰情况下的曲线跟踪状态良好;当加入了干扰之后,转速的误差值有了明显的变化,达到了±30 rad/s的误差;最后在引入干扰观测器的基础上进行控制,可以发现干扰得到了明显的抑制,转速误差最大值降到了5 rad/s左右。其中,线性化反馈控制器的参数k1=5 000 000,k2=500;干扰观测器的控制参数为b=1 500。
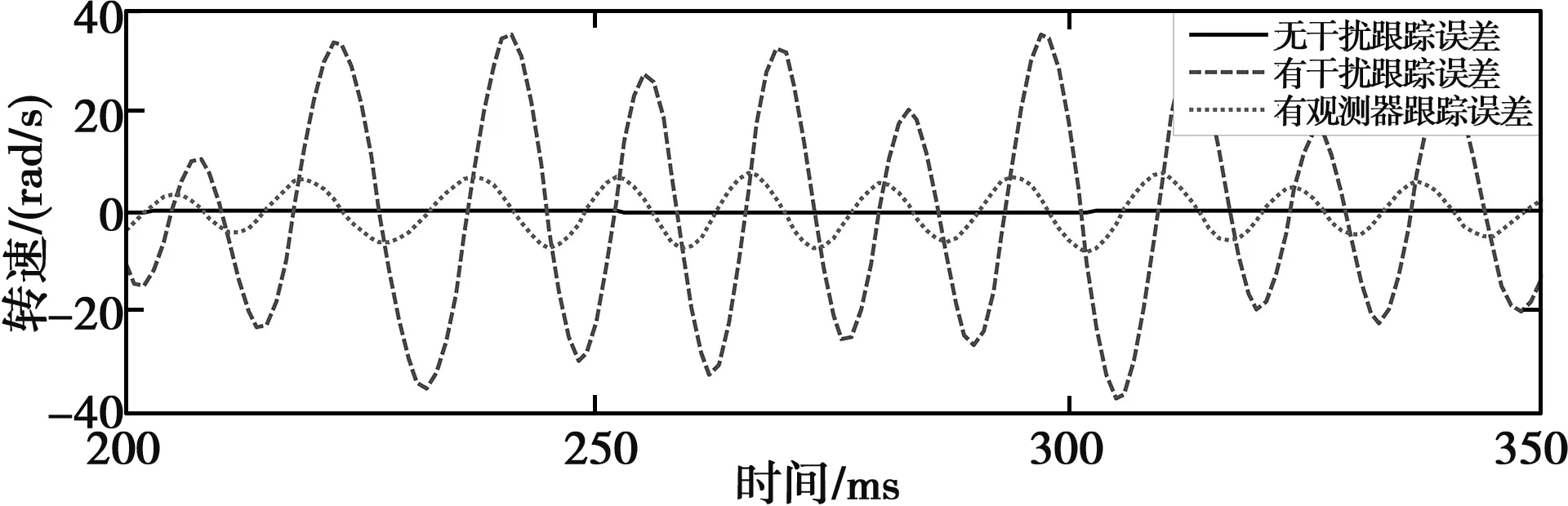
图6 3种状态下电机转速跟踪误差图
由仿真结果可以得出,本文提出的基于干扰观测器的反馈线性化控制策略能够很好地提高系统的控制精度和抑制外界干扰。
5 结束语
从上一章节的仿真实验可以看出,利用线性化反馈的方式成功地实现了对永磁同步电机的控制,在存在外界干扰时伺服系统的跟踪信号明显出现了波动,当加入了干扰观测器的补偿后跟踪误差明显变小。
综上所述,针对伺服控制系统中出现的非线性和外界干扰问题,本文通过线性化反馈的方式实现了永磁同步电机的控制,通过干扰观测器进一步地提高了系统的鲁棒性,能够有效提高控制精度。
