基于信号频域特性信号信噪比提高及分离

李 娟，戴曜泽，傅 雷

(1. 南京科瑞达有限责任公司，南京210008； 2. 中国航天科工集团8511研究所，南京210007)

0 引 言

信道化接收机采用滤波器组来分选不同频谱信号[1]。信道化接收机使用的前提是每个信道只有一个信号且信号不跨信道。若在一个信道上同时有两个信号或信号跨信道，这种输入条件就超出了信道化接收机的能力范围，很大可能会输出错误的频率信息。特别是随着电子技术的快速发展，波形复用、频率复用及大带宽线性调频、相位编码等复杂波形在新体制雷达的广泛应用[2]，使信道化接收机滤波器很难找到合适的带宽。当带宽太大时，信噪比的改善小，并可能会出现一个信道出现多个信号的情况。当带宽太小时，信噪比得到改善，但会使用更多的硬件资源，并可能出现信号跨多个信道的情况[3]。基于信道化接收机的上述情况，本文提出了一种基于频域的信号分离和信噪比提高方法。

目前，侦察接收机信号分离和信噪比提高大多基于时域的线性处理[4]，保留信号的相位信息。但是，在侦察接收机中信号的相位信息影响干涉仪测向和相位编码的恢复。因此，可以使用频域的非线性处理进行信号的脉内分析、分选、跟踪。信号的相位信息主要集中在频谱的主瓣和第1旁瓣。因此，在频域分离和滤波时保留第1旁瓣最大可能保留其相位信息。频域处理瞬时带宽大且不会出现跨信道情况，是一种实用的信号分离和信噪比提高算法。频域的信号分离及滤波主要基于信号的傅里叶变换及逆傅里叶变换，不涉及信号的矩阵运算复杂算法，是一种硬件可实现的实用算法。

1 算法原理

1.1 傅里叶变换

离散傅里叶变换[5]可表示为

(1)

式中，x(n)为接收到的时域信号，N为傅里叶变换的阶数。

离散傅里叶变换具有以下特点：

(1) 傅里叶变换系数实质就是信号在某一频率分量的幅度。任何信号的傅里叶变换都可看成多个频谱分量的叠加。

(2) 截断信号的傅里叶变换，时域相当于与矩形信号相乘，频域相当于与矩形信号频谱卷积。因此，截断信号频谱为sinc包络函数，保留主频率及第1旁瓣，将其余的频率清零，可以去除信号的噪声，提高信噪比。在频率清零的过程中，清除了部分频率，会对信号的相位造成影响，但因为清零的幅度很小，所以对相位的影响在可接收的范围。

(3) 傅里叶变换时，为了方便计算，经常在数据后面补零。补零并没有对原信号增加任何新信息，因此不能提高分辨率。频谱的物理分辨率是其积累时间决定的。所谓的补零增加分辨率仅仅是计算分辨率。数据的截断除了采样频率为载频的整数倍M且截断长度N是M的整数倍，频谱不发生泄露，其他情况要产生频率泄露，且数据过短补长零将严重影响对原频谱的辨认。

1.2 逆傅里叶变换

离散逆傅里叶变换可表示为

(2)

由式(2)可知，对信号频谱进行逆傅里叶变换可恢复出信号的时域波形。

2 算法实现

基于频域信号分离及信噪比提高的流程[6]如图1所示。根据中频信号傅里叶变换结果在频域确定噪声能量，由虚警概率和检测概率确定信号的判决门限，对信号进行分离。分离后的信号根据频谱幅度和频谱位置判断是否为同一信号，若为同一信号则进行合并。对合并后的信号进行逆傅里叶变换恢复时域信号，然后利用信号的时频特性对信号进行分析。此算法的关键点为噪声能量确定和信号的分离合并。以下就此关键点进行介绍。

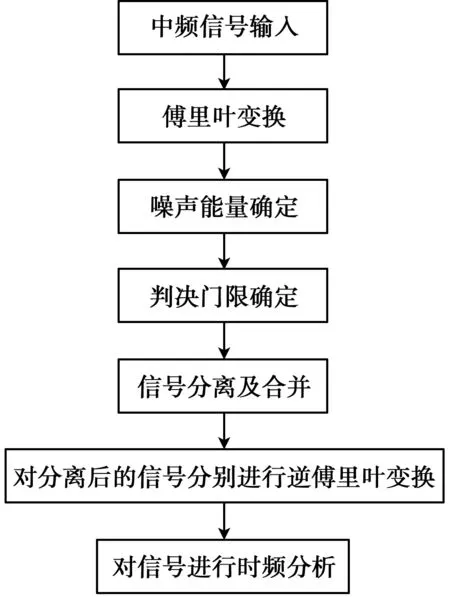
图1 信号分离及信噪比提高流程

2.1 噪声能量确定

设接收机截获信号为

x(n)=s(n)+w(n)

(3)

式中，s(n)为接收到的信号，信号的能量为A2；w(n)为均值为零，方差为σ2的高斯白噪声。由傅里叶变换的线性特性可得

x(f)=s(f)+w(f)

(4)

x(f)的二阶矩量M2为

M2=E[x(f)x*(f)]

=E{[s(f)+w(f)][s(f)+w(f)]*}

=E[s(f)s*(f)+s(f)w*(f)+s*(f)w(f)+

w(f)w*(f)]

(5)

根据能量守恒定律可得

M2=E[s(f)s*(f)]+E[s(f)w*(f)]+

E[s*(f)w(f)]+E[w(f)w*(f)]

=E[s(f)s*(f)]+E[w(f)w*(f)]

=A2+σ2

(6)

x(f)的四阶矩量M4为

M4=E{[x(f)x*(f)]2}

=E{s2(f)[s*(f)]2}+E{w2(f)[w*(f)]2}+

4E{|s(n)|2w(f)w*(f)}

=A4+2σ4+4A2σ2

(7)

由式(6)及(7)可得σ2的估计值为

(8)

在实际工程中，M2和M4的值可用以下表达式求出：

(9)

(10)

式中，N为信号的长度，x(f)为接收信号的傅里叶变换。

2.2 信号检测门限确定

信号总是伴随噪声而存在。侦察接收机接收的信号是各种射频信号。当没有接收信号时接收机接收的为纯噪声(w(n))，而当有信号时接收机接收的为信号加噪声(s(n)+w(n))。所谓的信号检测及分离就是在噪声背景中发现目标并将多目标进行分离。

侦察接收机检测信号的方法为门限检测，如图2所示。在接收机输出端设置一门限电平。当输出电压超过此门限时就判定为目标，电压未超过门限就认为是噪声。

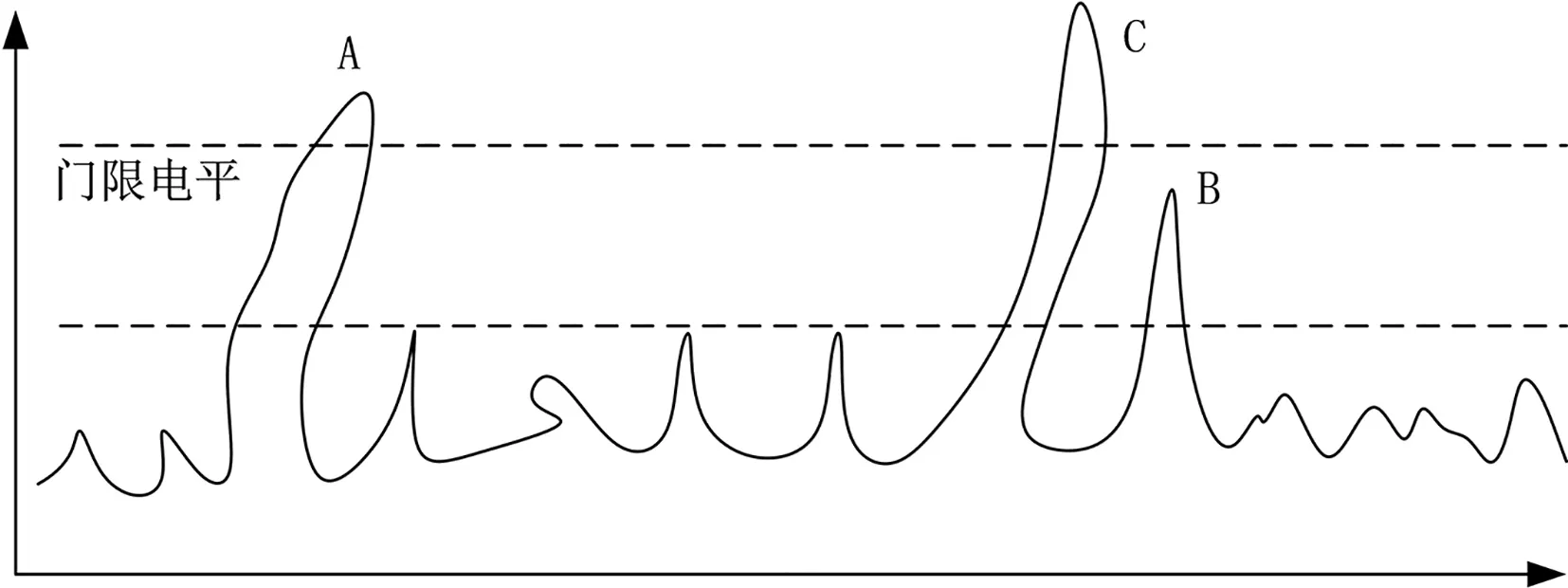
图2 门限检测

这样，就会出现下列几种情况：图中A处有一较强信号。它与噪声叠加后超过了门限，因而被判定为目标信号，这是正确的发现。图中B处也存在信号，但它与噪声叠加后未超过门限，因而未被判定为信号而当作噪声了，这是漏报。图中C处并没有信号，但噪声的尖峰超过了门限，因而被判定为信号，这称为虚警。

因此，信号检测性能的好坏可以用信号的检测概率和虚警概率这两个量值来衡量。在虚警概率一定的情况下，最大可能提高信号的检测概率。门限设置较高可以减少虚警概率，但是漏警概率会增大，从而使检测概率降低。门限设置较低，可以减少漏警概率，提高检测概率，但虚警概率会增大。因此，根据噪声的统计特性，在一定虚警概率情况下最大可能提高检测概率。一般门限电平比噪声能量高12 ～15 dB。

2.3 信号分离及合并

信号分离及合并的步骤如下：

(1) 对信号进行傅里叶变换，将时域信号转换为频域信号；

(2) 根据虚警概率、检测概率及噪声能量确定信号检测门限；

(3) 根据检测门限，在频域对信号进行分离，并记录信号出现的频谱位置及幅度；

(4) 根据频率分离的门限和信号出现的位置，对小于频率门限的多个信号进行合并；

(5) 对合并后的信号进行主瓣宽度和幅度提取；

(6) 根据信号的主瓣宽度和幅度，判断相邻的信号是否为主瓣与旁瓣的关系，若为主瓣与旁瓣关系则合并为一个信号；

(7) 对合并后的信号，取频谱的主瓣及第1旁瓣，其余的频率置零，滤除第1旁瓣以外的噪声，提高信噪比；

(8) 对分离和滤除噪声的信号进行逆傅里叶变换，将信号由频域恢复到时域，由信号的时域及频域特性对接收的信号进行分析。

3 仿真验证

3.1 仿真条件

信号的采样频率[6]fs=1.25 GHz，脉冲宽度PW=6.3 μs。脉冲有3个信号组成：中频频率f1=100 MHz的单频信号、中频频率f2=200 MHz及带宽BW=20 MHz的正线性调频信号、中频频率f3=300 MHz及带宽BW=10 MHz的二相编码信号，信号的输入信噪比SNR=0 dB。

3.2 仿真结果

3种波形及合成后的时域、频域波形如图3～6所示。由图3～6可看出，当SNR=0 dB时域信号无法分辨时只能通过频域信息对信号进行分离。利用第2章节的算法对单频、线调及二相编码3个信号进行分离，分离后的时域图、频域图及时频图如图7～12所示。由图7～12可看出，通过频域可分离同时到达信号，除主瓣和旁瓣以外其他频点置零操作可提高信号的信噪比，从而使信号的时频特性分析得以实现。基于频域信号分离和信噪比提高主要运用乘累加、傅里叶变换和逆傅里叶变换，是一种硬件可实现的实时算法。

图3 单频时域及频域波形

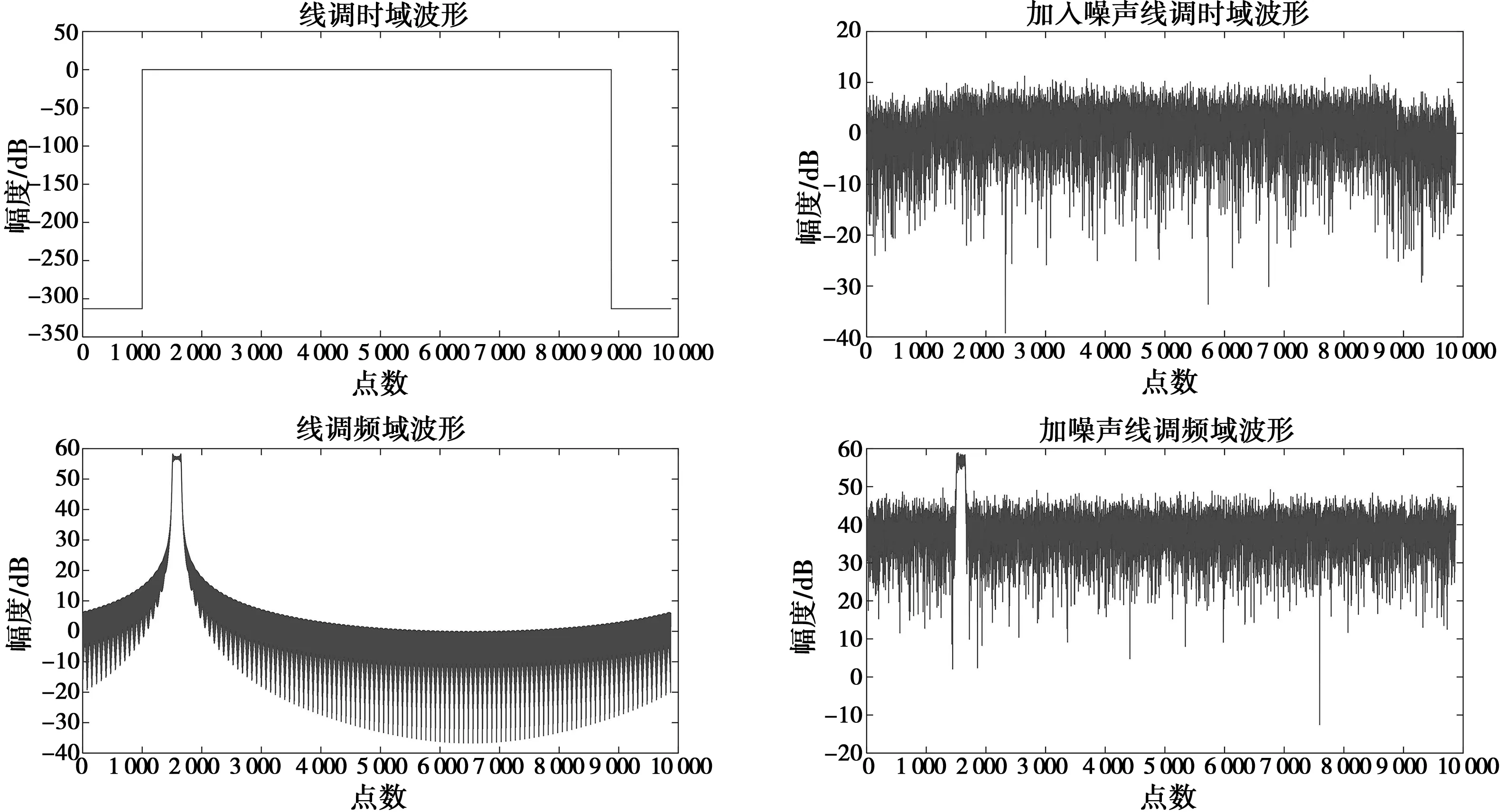
图4 线调时域及频域波形

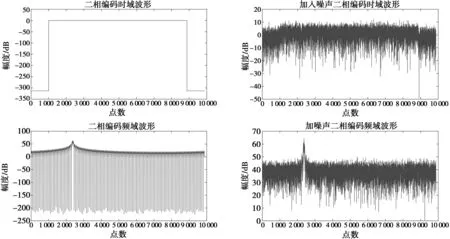
图5 相位编码时域及频域波形

图6 合成信号时域及频域波形

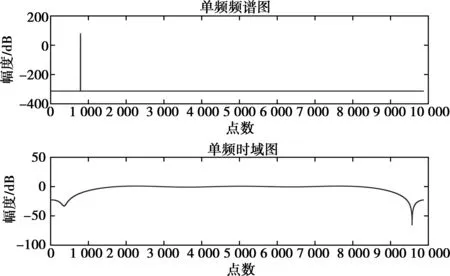
图7 单频信号时域及频域图

图8 线性调频时域及频谱图

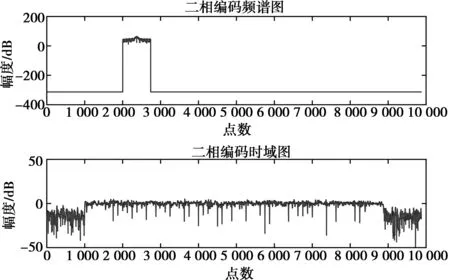
图9 相位编码时域及频域图

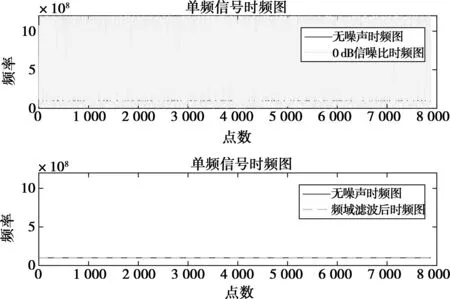
图10 单频信号时频图

4 结束语

基于频域的信号分离及信噪比提高的特点，本文首先介绍了算法实现原理和算法实现流程，然后通过仿真验证了此算法的有效性。本文算法在信号信噪比提高和信号分离过程中最大限度地保留了信号的相位特性和信号的包络特性，为后续的时域分析提供了数据基础。算法的实现主要基于乘累加的平方运算、傅里叶变换和逆傅里叶变换，是一种硬件可实现的算法，且实时处理能力较强。

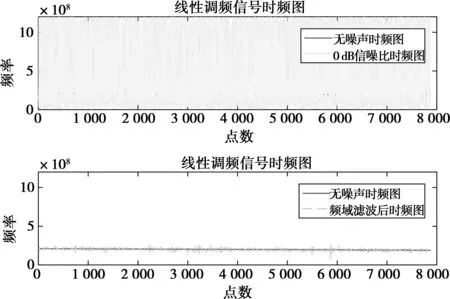
图11 线性调频时频图

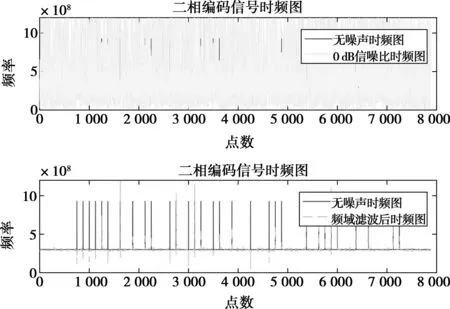
图12 相位编码时频图