高中数学教科书中的物理情境及其应用探析
2021-03-18唐海军王佳佳刘双陈芳芳
唐海军 王佳佳 刘双?陈芳芳


摘 要 此研究选取北师大版、人教A版、人教B版(2019版)高中数学教科书(必修)中的物理情境作为研究对象,对三版教科书中物理情境的分布特征、价值定位进行了分析。建议教科书编写者和使用者,以 情境“融合”为导向,优化教科书编排;以 学科“联系”为依托,提升教学设计功能;以 资源“创造”为平台,促进项目式的学习。
关键词 数学教科书 物理情境 情境价值
经济合作与发展组织(OECD)2018年发布的研究结果《OECD学习框架2030》提出:“未来的学生将需要广泛和专业的知识,作为发展形成新知识的基础学科知识仍然会是很重要的,但是还需要跨学科思维和‘连接的能力。”[1]随着数学教育的发展,部分国家较早地在高中数学课程改革中尝试跨学科、跨文化的课程融合,例如澳大利亚《高中数学课程标准》(2013版)中重视历史、文化传统和土著居民语言的融入[2]。法国《高中数学大纲》明确指出要将数学与物理等学科联系起来,并强调教学内容与实际应用相互联系,通过学生的探究来发现大千世界的奥妙[3]。中国《普通高中数学课程标准》(2017版)的内容中也已经呈现出跨学科融合现象。数学教科书中的物理情境作为服务于学习者数学学习,呈现数学概念、思想方法的跨学科背景材料,是连接STEAM教育与学科课堂的纽带。因此,在复合型人才培养的背景下,研究分析高中数学教科书中物理情境的分布特征、价值定位与应用实践,对完善数学教科书、改进教学和培育学生核心素养都具有十分重要的意义。
一、数学教科书中物理情境的分布特征
以北京师范大学出版社(简称,北师大版)、人民教育出版社(簡称,人教A版、人教B版)2019年发行的高中数学教科书(必修)作为物理情境的统计来源,以《普通高中数学课程标准(2017版)》(简称,数学课标)中必修课程所规定的5个主题及相应若干单元为“数学单元”的统计标准,结合《普通高中物理课程标准》(2017版)涉及的知识主题,分版本对涉及物理情境的数学单元、物理主题和教科书位置等进行了统计分析。
1.涉及物理情境的数学单元分布
三版教科书中涉及物理学知识的情境材料,出现在5个数学主题,9个单元之中,最终统计情境数目及相应数学单元分布,见表1。
由表1可知,北师大版、人教A版和人教B版教科书必修部分涉及物理学知识的分别有7,8,9个单元。物理情境在三个版本教科书中的总体分布比较集中在“平面向量及其应用”和“三角函数”两个单元。进一步分析这两个单元的内容,发现物理情境主要是分布在教科书中的“向量的加减运算”和“正弦型三角函数”等章节。上述统计数据,一方面说明新版高中数学教科书中拥有大量的物理学情境,教科书编写者力图让教科书能够引起学生的阅读和学习兴趣,突显教科书的“心理性”——即
学习素材的现实性、衔接性与可读性[4];另一方面反映出新版教科书重视向量作为联系物理与数学的纽带作用,强调三角函数作为描述周期现象的重要数学模型的地位,让师生能够进一步体会从实际问题中抽象出函数,就是在经历一个非常典型的数学建模过程。
2.教科书中的物理学主题分布
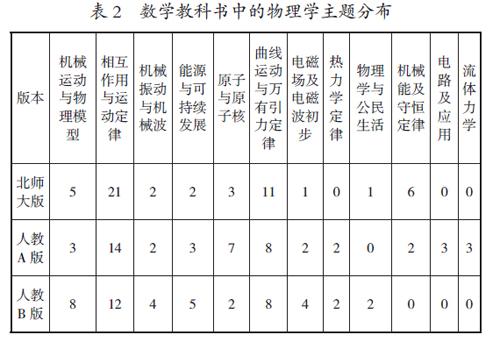
根据《普通高中物理课程标准》(2017版)所给出的23个规范性的物理“主题”名称以及表1所列章节数学内容对应的物理学知识,统计出教科书中物理学主题的分布情况,如表2所示。
由表2可知,北师大版、人教A版和人教B版教科书必修部分情境中出现的物理学主题分别有9、11和9个。上述内容主要是分布在“相互作用与运动定律”“曲线运动与万有引力定律”两个主题。进一步分析,这两个主题的内容对应数学中的向量和三角函数两个单元,也是2017版数学课标的教学案例编写建议中所明确提到的物理学内容。这反映了三版教科书编写者在情境编写时“忠实课标”,力求做到“按标编排”。数学教科书中的物理学主题分布特征,也与物理学科中数学需求特征是相互吻合的,即“高中物理课程学习中对向量运算知识的需要程度最高,而立体几何和概率统计需求程度最低”[5]。
3.物理情境所处教科书的栏目分布
物理情境在高中数学教科书中所处的栏目通常包括章节头、正文、例题、习题(复习题)、章节总结、拓展内容,统计其分布情况如表3所示。
主要是分布在习题栏目中(其中北师大版占55.77%;人教A版占59.18%,人教B版占40.43%),表明了三版教科书的编写者均倾向于将物理情境作为数学新知识巩固应用的场景。进一步分析,三个版本又各具特色,北师大版主要分布在习题、正文和例题中,人教A版分布在习题和例题中,而人教B版分布在正文和习题中。从栏目来看,人教A版各栏目均有分布,其中在指数函数一节的拓展部分设计了“放射性物质的衰减”作为阅读思考材料。此外,人教B版教科书必修部分的正文中出现的物理情境占其总体的42.55%,说明该版教科书有意在正文部分利用物理学情境,引导学生突破学科壁垒,在多学科的氛围中掌握各种知识与技能。
二、数学教科书物理情境的价值定位
教师在教学设计中利用教科书情境或创设教学情境,已成为教学工作中的一种“习惯”,然而审视教学,又“不难发现教师对问题情境的认识大多还停留在价值和意义的经验层面,即通过创设问题情境来解决学生诸如兴趣、动机等方面的问题”[6]。物理情境所具有的平台支撑、科学探究和文化育人等多重属性没有得到准确认识,多元功能有待情境的编制者和使用者充分挖掘。
1.指向素养的知识载体价值
教科书情境依据知识的类型、学习目标以及学习者的年龄特征而表现出不同的现实“画像”,但情境创设的核心在于数学素养的提升,关键在于为展开知识和思维的双过程营造场景[7]。因此,情境具有现实性和思考性的特征。“现实性”是情境的外显特征,涉及学生生活世界中的客观现实、已有的数学知识经验以及其他相关学科的知识经验等,这一层面是服务于学生知识的建构。“思考性”则体现了情境的核心价值,表现在情境所蕴含的数学活动中,这一特性旨在发展学生的数学思维,体现情境的支架作用[8]。每个情境都有相应的“话语”和“结构”来描述情境的“现实性”和“思考性”。话语是描述其情境内容的元素(包含用词、符号、图案、表格),结构是呈现情境所涉及的知识之间的关系。
例如,北师大版2019年高中数学教科书必修第二册“6.2平面向量在几何、物理中的应用”一节中的例18,在“悬挂灯具”这一情境中,既包括问题情境的求解,又蕴含模型情境的应用。它涉及的物理学背景知识是“力的相互作用与运动定律”,物理学的话语有“拉力”“重力”,而结构就是等量关系“重力=两绳拉力合力”,数学符号表征为“ F1 cos60°+ F2 cos60°= G=10”。在情境层面,物理学知识不是情境的点缀,而是为引出问题中存在的“物体受力模型”,这一模型可以用“向量”语言直观地表达。通过例题,凸显向量是解决许多物理与数学问题的有力工具。
2.主题聚焦的科学研究价值
科学与数学是人类探究自然、了解自我的重要工具,也是社会与经济发展的催化剂。科学能力与数学能力息息相关。例如,为了保持科学与工程领域的世界领先地位,英国皇家学会于2014年6月26日发布了题为《科学与数学教育愿景》的政策咨询报告,为未来20年英国教育体系改革绘制了路线图,并着重建议将数学和科学课程作为必修课,延续至义务教育最后阶段,以提升国民科技素养、满足未来人才需求[9]。PISA2015测试显示中国大陆学生科学素养排名第10,低于数学的排名。在促进科学与数学素养的提升方面,中国教育部陆续出台具有整合特征的政策文件,如《关于“十三五”期间全面深入推进教育信息化工作的指导意见》《中小学综合实践活动课程指导纲要》来推动科学、工程、技术与数学的融合。教育研究人员指出,“现实学校教育中,教师很难在STEAM学科之间建立联系。因此,当学生以孤立和分离的方式学习时,他们往往对科学和数学不感兴趣,因为他们缺少与横切概念和现实世界应用程序的联系”[10]。物理情境则为教师的教科书“二次开发”与跨学科教学设计提供了契机。
例如,人教A版2019年高中数学教科书必修第一册“4.2指数函数”的问题2,“当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为‘半衰期。按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?”
“碳14的衰减”这一情境在三个版本的教科书中都有出现,(北师大版3次,人教A版6次,人教B版2次),可见这个物理情境的重要性。目前,北师大版将这一情境放在对数函数的概念与性质的学习中,人教A版主要是将这一情节作为指数函数的引入例题、课后习题和阅读材料。而人教B版将其分别放入到指数、对数函数的学习之中,目的是建立起指数函数与对数函数的联系。其实,这一内容的科学研究价值远远没有被充分利用起来。从数学学科来看,指数函数是刻画现实世界规律的一个重要模型,放射性物质衰变中半衰期的研究不但涉及物理学,还包括化学、生物学、天文学以及考古学动植物年代研究等等。从STEAM视角,围绕放射性物质衰变这一科学概念,教师在课后组织学生经历科学的探究过程,设计一系列的科学情境,从而加深学生对指数与对数函数模型的理解以及科学与人文素养的培养。
3.情境熏陶的文化育人价值
数学课标(2017版)指出数学教育承载着落实立德树人根本任务和发展素质教育的功能。特别强调数学教育除了帮助学生掌握学习和生活所必需的数学知识、技能、思想和方法以外,还特别提及需要增强学生社会责任感,在学生形成正确人生观、价值观、世界观等方面发挥独特作用。这与著名的华德福(Waldorf)教育目标是一致的,即教育还需要能够培养一个了解世界、人类历史文化,具有多种实践能力和艺术才能,对自然世界怀有深深的敬畏之心,并与之交流的人。2019版高中数学教科书在回应课标要求的同时,也通过情境的编排来体现物理情境的文化育人价值,彰显“文化自信”。例如,人教A版必修第一册中“第5·6节匀速圆周运动的数学模型”。
该情境是用数学中的三角函数模型来刻画筒车的运动规律,涵盖了圆周运动(角速度、转动惯量、角动量等)以及势能与动能的转化等物理知识。该情境还体现出中国的传统农耕文化中利用科学知识提高生产力的现象。农耕文化是中国劳动人民几千年生产生活的智慧结晶,是以不同于常见形式沿袭下来的一种文化形态。在正弦型函数学习中引入筒车这一农耕文化符号,不仅体现了正弦型函数可以描述周期运动,更突显了情境的科学性、观赏性、趣味性等特征。教科书中回归并记录了农耕文化的痕迹,拉近了城乡学生文化心理距离。在学习中不仅可以了解传统农耕文化和民族历史,还可以起到“降低碳排放、使用绿色能源”的环保教育作用。
三、数学教科书中物理情境的应用策略
经合组织(OECD)在2019年发布的《PISA2018见解和解释》中提出:未来的教育需要的是融合,不同学科的融合,不同学生的融合,各种学习情境的融合;需要的是联系,与现实世界情境的联系,与社区丰富的资源的联系;需要的是共同创造,承认学生和成年人都是学习设计成功的资源[11]。所以,数学教科书中物理情境的开发、应用需着眼于教材情境的“融合”、教学设计的“联系”与学习资源的“创造”三个维度。
1.以情境“融合”为导向,优化教科书编排
数学与物理的融合有着悠久的历史,科学史上很多知名的物理学家也是数学家。正如弗赖登塔尔指出,数学家“以物理观念为向导创立了一整套的方法,它们变成了现代偏微分方程论、积分方程论和泛函分析中的典范”。數学的发展不断地从应用中获得刺激,“如果没有应用的推动,数学会变得多么贫乏”[12]。数学课标(2017版)中明确地在必修和选修系列课程中提出了较多的与物理学主题相关的情境要求。比如,在选择性必修中,建议将一元函数导数及其应用与物理情境结合起来开展教学。引导学生经历一个由平均变化率过渡到瞬时变化率的过程,从而更好地与大学数学内容衔接[13]。所以,数学教科书融入一些符合学生认知水平和课堂教学特征的科学类情境尤为重要。
(1)对比不同版本教科书来调整问题情境
其一,参考国外教科书编制经验。以法国数学教科书为例,由于数学与物理学科的紧密联系一直是法国数学教育的一个典型特征。为增强数学和科学学科的联系,高二年级引入跨学科项目(The multidisciplinary projects),称为TPE,比如在高三设置一些与放射性活动相关的跨学科工作,以引入指数函数的新模型[14]。其二,国内教科书情境编写以课标建议为指南。例如,课标建议教科书编制用正弦函数刻画三种周期变化的现象:简谐振动(单摆、弹簧等)、声波(音叉发出的纯音)、交变电流的物理情境。对此,三版数学教科书都有编写,但又呈现出不同的风格。
(2)保留以往数学教科书中的经典物理情境
人教A版(2004年)必修1习题1、必修2的第13题喷水池喷水头的设计,这个情境涉及的数学知识主要是二次函数的图象与最值,与物理学中平抛运动相关。喷水池这样的情境在平时的学校、公园、小区都能够见到,保留在教科书中,既可以做到数学与物理学科知识的融合,又能够引发学生关注和热爱生活,增强知识服务于生活实践的体验。
2.以学科“联系”为依托,提升教学设计功能
随着学科知识结构的演化和知识生产从模式1(特定学科)向模式2(跨学科)的转化[15],学科之间的边界和区隔逐渐消弭,知识的交叉与联系已成为近年大学专业设置和课程架构的重要趋势,若学生在高中阶段的数学学习就能够打破科目壁垒,去尝试与其他学科建立联结,扩大知识视野与培养跨界思维能力,将有助于其更好地适应未来大学的学习模式。从学科联系来看,数学教科书中的物理情境就为实施有“联系”的教学设计提供了契机,因而教师应充分利用情境的价值,围绕一个主题,从“横向整合”“纵向联系”来设计教学。
例如,北师大版必修1第五章复习题中有这样一个情境:飞行员从飞机上跳伞,第1s下落约16英尺,第2s下落约48英尺,第3s下落约80英尺,如果空气阻力不计,那么在第10s内,飞行员下落的距离是多少?
基于跨学科内容整合与合作问题解决,教师可如下设计教学:
情境创设:通过多媒体出示飞行员跳伞训练的新闻,引起学生对跳伞情境的兴趣,了解情境包含的相关数据。
提出问题:如何得出在第10s内,飞行员下落的距离是多少?你能提出好的建议吗?
解决问题:以动画展示飞行员跳伞过程,并过渡到质点的运动过程;学生自主思考、小组讨论运动轨迹的特点;教师指导学生思考“飞行员下落的时间(横轴)与下落的距离(纵轴)之间的函数关系”或直接展示取得探究进展的小组成果。
分享评价:学生组内、组间交流和全班分享,评估用模型g(t)=16t 2来描述该飞行员跳伞运动轨迹是否合理,从而获得模型的准确表达式。
拓展运用:学生总结整个过程中遇到的困难,思考是如何突破困难的,进一步思考:如果跳伞运动员从离地面2500m的高空跳伞,并准备在距地面500m时打开降落伞,那么跳伞运动员应在离开飞机多少秒后打开降落伞(精确到0.1s)?
跳伞是从生活中提取出来的情境。通过五个教学环节的设计,有利于学生在面对简化的现实生活场景,综合运用物理学、数学知识,发现问题、解决问题和拓展问题,从而支持学生经历一个用数学眼光观察世界,用数学思维思考世界,用数学语言表达世界的过程。
3.以资源“创造”为平台,促进项目式学习
从学生视角来看,“数学与现实生活的联系是什么?数学学习的意义究竟在哪里?”弗赖登塔尔认为教师“不要教孤立的片断,应该教连贯的材料,……因为有联系的事物学生学得快,记得
牢”[16],做到有联系地理解。教师通过挖掘数学教科书中物理情境的多元价值,建立资源“创造”的平台,指导学生参与跨学科融合的“小微”项目研究,来回应学生的疑惑。“小微”项目建设是师生运用数学的算理分析与逻辑,结合物理、化学和生物等学科知识,来解决自然科学现象,创造更多学习资源的活动。
从对教科书中涉及到的物理情境的统计来看,可以在如下几个主题内容方面建设项目式学习的资源库,见表4。
例如,在人教B版(2007年)数学选修4-4中《1.4圆的极坐标方程》内容后的探索与研究栏目中有如下一道关于航天器轨迹方程的题目:“神舟五号”载人飞船的运行轨道是以地心为焦点的椭圆,近地点高度为200km,远地点高度为350km。求轨道参数e、p。
对于“人造卫星”“载人飞船”这一类问题,学生在不同学段、不同学科中(特别是科学课程)有学习的经历,但那些经历中更多关心的是科学现象,而忽略了这中间的数学原理。这个探究项目的出发点就是立足物理情境中涉及的数学知识,进一步认识应用数学刻画运动规律。基于物理学视角,从万有引力定律出发,能够得到人造卫星或者宇宙飞船轨道的方程,且其轨道是圆锥曲线。从数学看,圆锥曲线的很多优美的光学性质,对探索宇宙奥秘有着极为重要的意义和价值;从内容与社会热点来看“载人飞船”在激发学生的爱国热情、培育科学信念和数学素养方面是极佳的物理素材。
总之,STEAM教育在国内影响不断扩大时,我们既要看到跨学科融合的优势,同时也要对此保持一份谨慎和理性。课程的分化与综合是社会分工与教育进化的必然结果,不同的课程在人才培养方面具有独特的功能。如果因为数学课程也具有陶冶学生科学素养的功能,而在教科书情境编制上过度选择物理情境,則偏离了数学课程的基本理念与性质,产生了“喧宾夺主”的效应,所以情境的编制与使用者对问题情境在数学学习中的意义都需要有一个清醒的认识。“首先,数学本质上是一门形式的科学,因此,在处理实际问题时应该强调的是‘数学化的过程;其次,要强调背景的数学意义,而不只是给数学问题穿上一件背景的外套。”[17]
参考文献
[1] 经济合作与发展组织(OECD).OECD学习框架2030[J].孟鸿伟,译.开放学习研究.2018,23(03):9-19.
[2][3] 史宁中,孔凡哲.十二个国家普通高中数学课程标准国际比较研究[M].长沙:湖南教育出版社,2013:87-88,144-166.
[4] 章建躍.高中数学教材落实核心素养的几点思考[J].课程·教材·教法,2016,36(07):44-49.
[5] 袁丽.中学物理课程中数学知识的支持性研究[D].重庆:西南大学博士学位论文,2009:52.
[6][8] 任旭.问题情境的创设:基于思维发展的理解[J].数学教育学报,2017,26(04):15-18.
[7] 王嵘.以函数为例,谈高中数学教科书的情境创设[J].中学数学教学参考(上旬),2019(02):11-13.
[9] 翟俊卿,阚阅,杨迪.英国《科学与数学教育愿景》评析[J].全球教育展望,2015,44(08):55-62
[10] Kelley T R,Knowles J G . A conceptual framework for integrated STEM education[J]. International Journal of STEM Education,2015,3(01):11.
[11] Andreas Schleicher.PISA 2018 Insights and Interpretations[M].
Paris :OECD Publishing, 2019:55-56.
[12][16] 弗赖登塔尔.作为教育任务的数学[M].陈昌平,唐瑞芬,等,译.上海:上海教育出版社,1995:14-16,72-73.
[13] 曹一鸣,严虹.高中数学课程内容及其分布的国际比较[J].数学通报,2015,54(07):9-14.
[14] 阿蒂格.法国高中数学教学[J].郭玉峰,整理.数学通报.2009,48(12):1-4.
[15] 吉本斯,等.知识生产的新模式:当代社会科学与研究的动力学[M].陈洪捷,沈文钦,译.北京:北京大学出版社,2011:3.
[17] 鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:185-186
[作者:唐海军(1982-),男,四川南充人,四川文理学院数学学院,讲师,贵州师范大学数学科学学院,博士生;王佳佳(1993-),女,四川达州人,四川文理学院数学学院,助教,硕士;刘双(1990-),女,四川达州人,四川文理学院数学学院,助教,硕士;陈芳芳(1989-),女,四川达州人,四川文理学院数学学院,助教,硕士。]
【责任编辑 孙晓雯】
