桥式起重机制动阶段防摇控制方案研究*

周奇才，张 蕴，熊肖磊，赵 炯

(同济大学 机械与能源工程学院，上海 201804)

0 引言

桥式起重机是物料搬运中使用范围最广、数量最多的起重机械设备，广泛应用于港口装卸、工业生产及设备安装等作业场合。桥式起重机主要结构包括驱动装置、卷扬装置、吊钩及行走机构等，卷扬装置通过柔性连接与吊钩相连，行走机构的加、减速过程会导致吊重摆动，对生产效率影响很大。

目前桥机防摇方法研究主要是基于现代及智能控制理论展开的，如：Wang X基于前馈控制设计了零振动(ZV)、零振动和微分(ZVD)、超灵敏(EI)三种输入整形控制器[1]；Ermidoro M提出了用定阶增益调度控制来减少摆长改变对吊重摆动影响的方法[2]；刘宏博基于批次控制和模糊控制进行了防摇仿真设计[3]；Frikha S将神经网络与滑模控制结合设计了神经与补偿防摇控制器[4]。

在桥式起重机整个运行过程中，制动阶段防摇效果对于系统的精准定位和生产效率起着决定性作用。而基于控制理论设计的防摇算法所计算出的运行机构期望速度曲线，其在制动阶段往往不能很好地适用，需要根据实际系统制动特点进行调整，如：王广超针对小车制动过程设计了来回梯形速度变换的防摇策略[5]；蔡威基于ABB电子防摇装置重新设计了制动阶段速度曲线[6]。

本文在采用状态反馈、软测量[7]等方法为变频调速桥机设计防摇控制系统的基础上,根据桥机制动阶段期望速度曲线，分析了控制系统制动阶段防摇效果不佳的原因及控制系统主导参数对制动阶段防摇效果的影响，提出了三种提高制动阶段防摇效果的方法，并基于实际样机对三种方法进行了测试。

1 桥机控制系统

1.1 系统概述

本文以一台16 t欧式双梁桥机为主要研究对象。桥机如图1所示，其支持远程控制和遥控两种控制方式，通过可编程逻辑控制器(PLC)控制变频器驱动桥机运行机构，PLC为LS产电XGB系列PLC，变频器为LS产电IS7通用矢量变频器。

图1 实际桥机系统

1.2 防摇控制系统设计

桥机系统大、小车分别有4档可操作速度档位，4档为最高速度档位，大车最高档速度为60 m/min，小车最高档速度为33 m/min，大、小车最低档速度均为最高档速度的十分之一。大、小车各自的最高速度都对应于变频器额定输出频率50 Hz，运行速度v与变频器输出频率f可以视作呈线性关系，即：

v=kf.

(1)

其中：k为变频器输出频率f与小车速度v之比。

该桥机系统防摇的目标是使桥机在达到档位对应速度的同时降低吊重的摆幅。分析系统情况后基于文献[7]提出的定速防摇策略进行了控制系统设计，即根据系统状态方程(2)进行极点配置设计了反馈控制系统：

(2)

其中：x1、x2、ξ为三个状态变量，x1=θ为吊重摆角，x2无实际物理意义，为了简化控制方程选取，ξ为当前速度与目标速度差值；l为等效摆长；g为重力加速度；vm为目标速度。

2 制动阶段防摇效果分析

将设计的反馈控制系统离散化后编入PLC中，带有控制策略的桥机小车在满速空载情况下启动及运行过程中吊重摆幅明显减小，但制动过程吊重摆动无明显改善。

2.1 离散系统仿真

基于小车和离散控制模型进行MATLAB仿真，基本参数为：变频器输出频率f与小车速度v比例k为0.011，吊重摆长l为8 m，桥机系统PLC程序扫描周期为14 ms，考虑通信时间等其他因素，设定仿真采样时间T为0.02 s。

仿真模型系统输入模拟桥机系统多档位的控制方式，输入曲线如图2所示。图2中，目标速度曲线呈阶梯状，即小车在达到4档速度后一段时间制动；计算速度曲线为控制模型计算出的小车速度期望曲线，可以看出在制动过程中，速度曲线出现明显的反向超调，即速度小于零的情况，这对于实际运行机构无法实现，分析认为这是桥机制动阶段防摇效果不明显的主要原因。

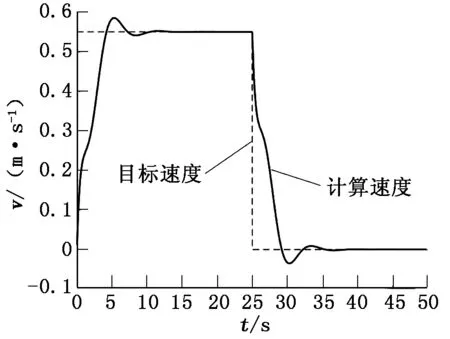
图2 速度随时间变化曲线

2.2 控制系统主导参数影响分析

在利用极点配置法设计状态反馈矩阵时，状态反馈矩阵K由式(3)确定：

|sI-(A-BK)|=(s-μ1)(s-μ2)(s-μ3).

(3)

其中：I为三阶单位矩阵；A、B分别为加入反馈后的系统矩阵和输入矩阵；μ1、μ2、μ3为系统闭环期望极点。通常三阶系统被当成1个二阶系统和1个一阶系统串联，故对应极点有：

(4)

其中：ωn为无阻尼自然频率；ζ为阻尼比；n为三极点实部倍数。

ωn、ζ和n是影响系统控制性能的主导参数。由于一般一阶系统的极点μ3配置在s平面离二阶系统一对共轭极点较远的实轴上，故其对系统影响很小，二阶系统的两个极点对系统的瞬态响应特征起主导作用。

无阻尼自然频率ωn主要影响系统的上升时间，ωn增大，系统上升时间降低，运行机构加速度增大，而加速度增大会在制动阶段产生冲击，使吊重摆幅增大。同时实际系统中，ωn受到变频器最高频率变化率的限制，不能取得过大。

阻尼比ζ对超调量大小起主导作用，ζ越大，系统的超调量越小，但系统上升时间和峰值时间增加，其对系统影响如图3、图4所示。从图3和图4可以看出：当ζ足够大，如ζ=0.9时，系统反向超调完全消除，但理论吊重摆幅也相应增大，无法达到既消除反向超调同时又减小吊重摆幅的目的；同时，ζ增大也增加了系统制动时间，对于实际系统需要留给制动器更多的延时抱闸时间，运行机构制动距离变长。

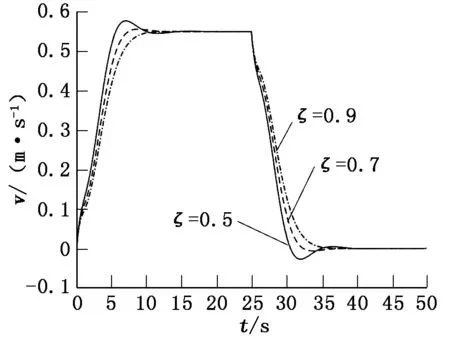
图3 不同阻尼比的速度随时间变化曲线

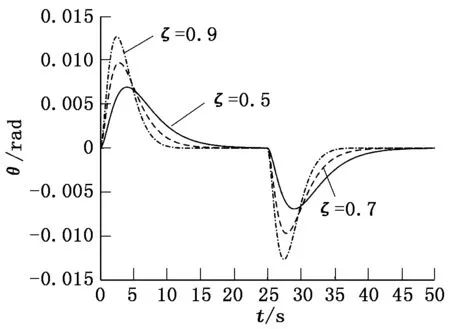
图4 不同阻尼比的摆角随时间变化曲线

因此在制动阶段，控制算法应在满足系统制动需求的情况下适当减小ωn，同时增大ζ，以降低反向超调对制动阶段防摇效果的影响并减小吊重摆幅。

3 制动阶段控制策略

除了在制动时通过改变原有控制系统主导参数来减小反向超调对系统控制效果的影响外，也可以通过直接改变制动阶段控制策略来达到快速消摆的目的。

3.1 分段减速制动

制动阶段常见控制策略是模拟司机操作桥机制动的过程进行分段减速制动，即先由高速档位减速到低速档位，等到速度稳定后再由低速档位直接制动，其仿真结果如图5所示。由图5可见：低速档位直接制动几乎没有反向超调，反向超调仅对减速第一阶段有影响，同时吊重摆幅显著减小。但此类方法存在制动时间和距离过长的问题，接收制动指令后，运行机构需要继续运行一段时间才能停下，司机操作时往往需要根据经验进行提前制动。因此此类方法只适用于对定位精度要求不高并拥有较长制动距离的场合，而对于定位精度要求高的桥机系统则需要在原有控制系统中加入位置反馈，通过位置反馈计算出制动指令的给出时间，以确保桥机能够停留在指定位置。

图5 分段减速制动仿真结果

3.2 去除反向调整制动

对于期望制动后运行机构迅速制动，定位要求高又缺乏位置控制的桥机系统，可以采用去掉制动阶段反向调整制动的方法，即在计算频率f低于一定值f0(f0≥0)时直接取f=f0，然后延迟一段时间t后由制动器直接抱闸制动。此方法由于去掉了反向调整过程，吊钩摆角理论上不会直接衰减至0，而是呈衰减震荡(如图6所示)，选择的截止频率f0越小，衰减震荡最大摆幅越小，但最大摆幅随f0变化率也随之减小，在f0足够小后其对衰减震荡最大摆幅的影响可忽略。f0减小也会相应地增加整体制动时间，建议f0选择为制动前速度对应控制频率的1/50～1/100。

图6 去除反向调整制动仿真结果

在衰减震荡一段时间t后，桥机直接抱闸制动，吊重摆角会在自重、冲击等因素作用下迅速衰减至0。延迟时间t对该策略防摇效果影响很大，t应该根据吊钩摆动相位确定，但对于无摆角检测装置或采用软测量方法的桥机系统而言吊钩实质摆动相位难以确定，可以通过实际系统进行试凑确定t。

4 实机试验

在本文所研究的实际桥机系统上对以上提出的三种方法进行测试，由于试验条件限制，桥机系统只能空载运行，吊重摆幅只能通过摄像机粗略测量其制动时吊重摆动的最大幅值，分别在吊重摆长为6 m、8 m的满速空载小车上对三种方法进行了试验。制动防摇效果主要通过多次重复试验下测出的吊重最大摆幅平均值界定。

方法一是通过改变制动阶段控制系统主导参数减小反向超调来降低吊重摆幅，试验发现制动阶段适当增大阻尼比ζ或减小无阻尼自然频率ωn均对吊重摆角影响较小，摆长6 m时吊重摆幅在250 mm～300 mm之间，摆长8 m时则在350 mm～420 mm之间，而大幅改变ζ或ωn会造成控制系统失控，桥机系统出现无法正常启停现象，分析认为空载试验时风力、空气阻力等对系统影响较大，导致系统对控制系统参数敏感度降低；方法二为分段减速制动，在给出制动指令后，系统会先由4档减至1档速度一段时间后再制动，此方法效果明显，在制动时间保证的情况下两种摆长下吊重摆幅可减至40 mm左右，但其制动距离相比方法一和方法三大幅增加；方法三为去除反向调整制动，f0选为1 Hz，通过试凑法改变延迟时间，得到了较好的效果，摆长6 m时吊重摆幅140 mm左右，摆长8 m时吊重摆幅190 mm左右。

5 结论

本文从变频控制的桥机系统出发，根据文献[7]建立了防摇控制系统，重点对桥机制动阶段防摇控制方案进行了研究，提出了三种改进方法并在实际桥机上进行了试验，得出了以下结论：①对于实际桥机系统，制动阶段速度反向超调无法实现，是桥机制动时防摇效果不明显的主要原因，在设计控制算法时应尽量避免；②对于本文研究对象，去除反向调整制动方法综合效果最佳，能满足系统对防摇效果和定位精度的要求。

需要说明的是，由于试验条件限制，本文所使用的系统模型与实际模型有一定差距，未考虑空气阻力、风力等因素，试验结果对理论分析支撑不足。因此本文仅供实际应用参考，方法一中控制主导参数对桥机制动阶段防摇效果的影响、方法三中延迟时间的确定方法等问题还有待进一步研究。