整车热管理系统方案设计
2021-03-18刘校兵严俊杰岳明辉
刘校兵, 胡 飚, 严俊杰, 王 鑫, 岳明辉
(重庆长安汽车股份有限公司, 重庆 400023)
汽车研发是一个复杂的过程,具有多层次、多系统且系统之间相互耦合等特点[1]。在整车架构中,热管理系统是典型的复杂系统,主要包括发动机冷却系统、润滑系统、进排气系统、空调系统等多个热流体系统,其性能直接影响到整车动力性、燃油经济性、排放和乘坐舒适性。当前,对于整车热管理系统的研究主要有以下两个方面。一方面是以单个系统为研究对象,使其性能最优,缺乏对子系统之间相互影响的考虑[2-4];另一方面是结合动力系统,建立热管理系统模型,对系统性能进行综合研究。李靖[5]结合Chen等[6]的研究成果建立了完整的热管理系统,并分析了子系统之间相互影响;唐沛翔[7]利用AVL_Cruise和AMESim软件也建立了整车热管理系统的仿真模型,并以燃油经济性和排放性能为目标函数进行了多目标优化。但是,在整车开发过程中,仅仅考虑性能最优,还不足以指导系统的选型设计。因此,需要对性能、成本及重量等属性进行综合评价,才能在实际工程运用中设计出全局最优的系统方案。
针对产品多属性综合评价问题,层次分析法是一个有效的解决方案[8]。层次分析法是20世纪70年代美国运筹学专家Saaty提出的一种定性与定量分析相结合的系统的、层次化的分析方法[9]。该方法曾广泛应用于航空[10]、船舶领域[11-12],近些年在汽车领域也有所应用,如基于主观评价的造型方案选型[13-14]、排气系统悬挂点位置优化[15]、汽车工业的人因可靠性分析技术选择[16]等。
本文以整车热管理系统为研究对象,在多系统联合仿真及多目标优化基础上,利用层次分析法和加权评分模型,对优化得到的Pareto方案集进行综合评价,得到全局最优的系统方案。
1 方法介绍
首先,采用先部件建模、后系统集成的方式建立一维多系统联合仿真模型。然后,建立多目标优化模型,采用多目标粒子群算法进行寻优求解,得到Pareto方案集[17-18]。最后,采用层次分析法和加权评分模型对Pareto方案集中的各方案进行综合评价。设计流程如图1所示。
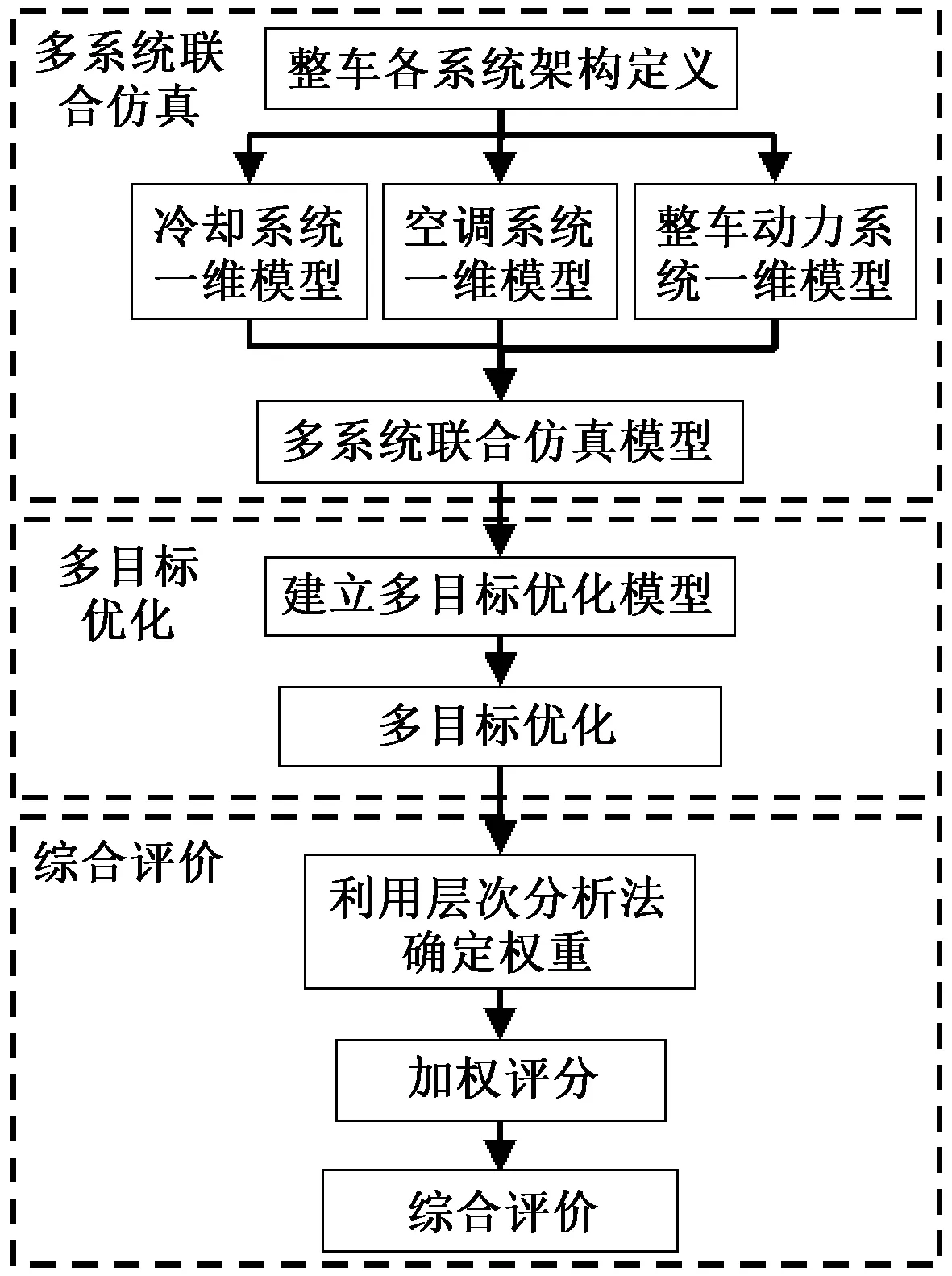
图1 热管理系统方案设计流程
2 仿真模型
2.1 单系统一维仿真模型
建立发动机冷却系统仿真模型如图2所示,包括冷却水循环、发动机机油回路、变速器油侧边界,其中冷却水循环包含3个回路,即发动机-散热器、发动机-机油冷却器、发动机-暖通芯体-变速器。建立空调系统仿真模型如图3所示,包含两相流回路和乘员舱热舒适性模型。
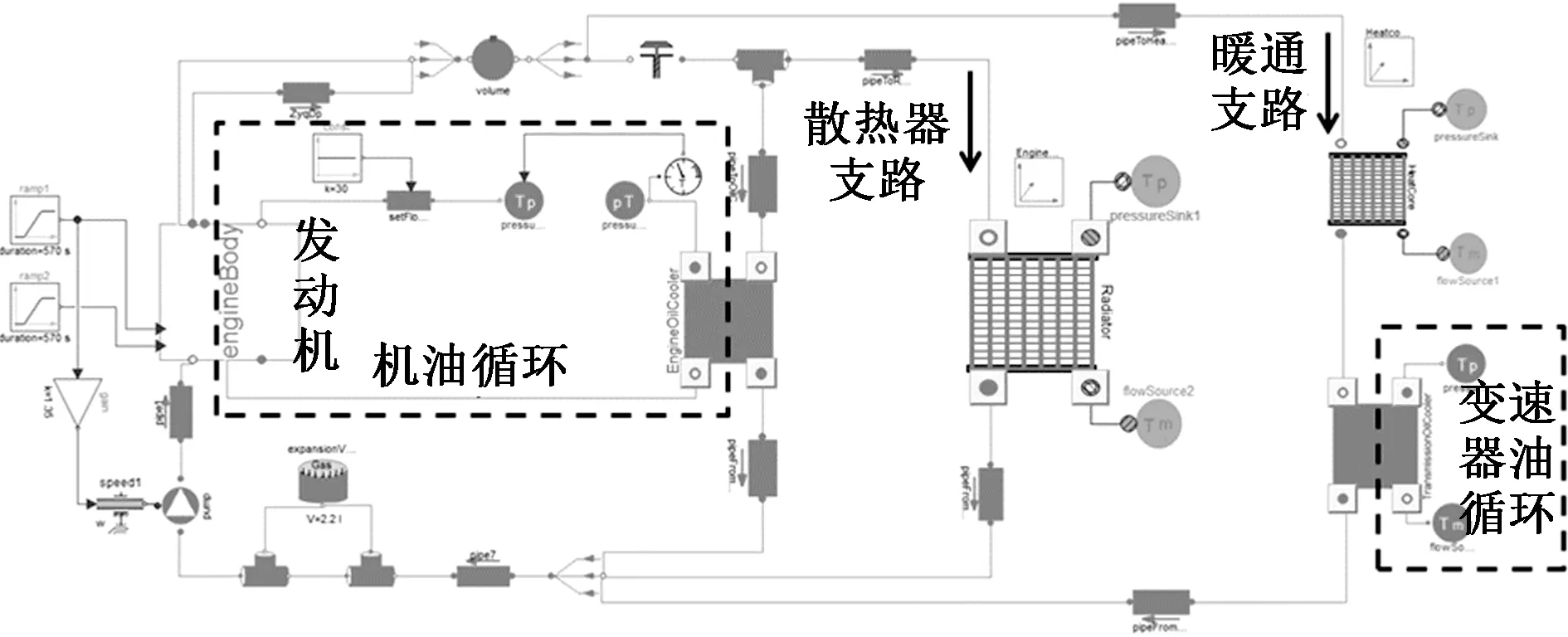
图2 冷却系统模型
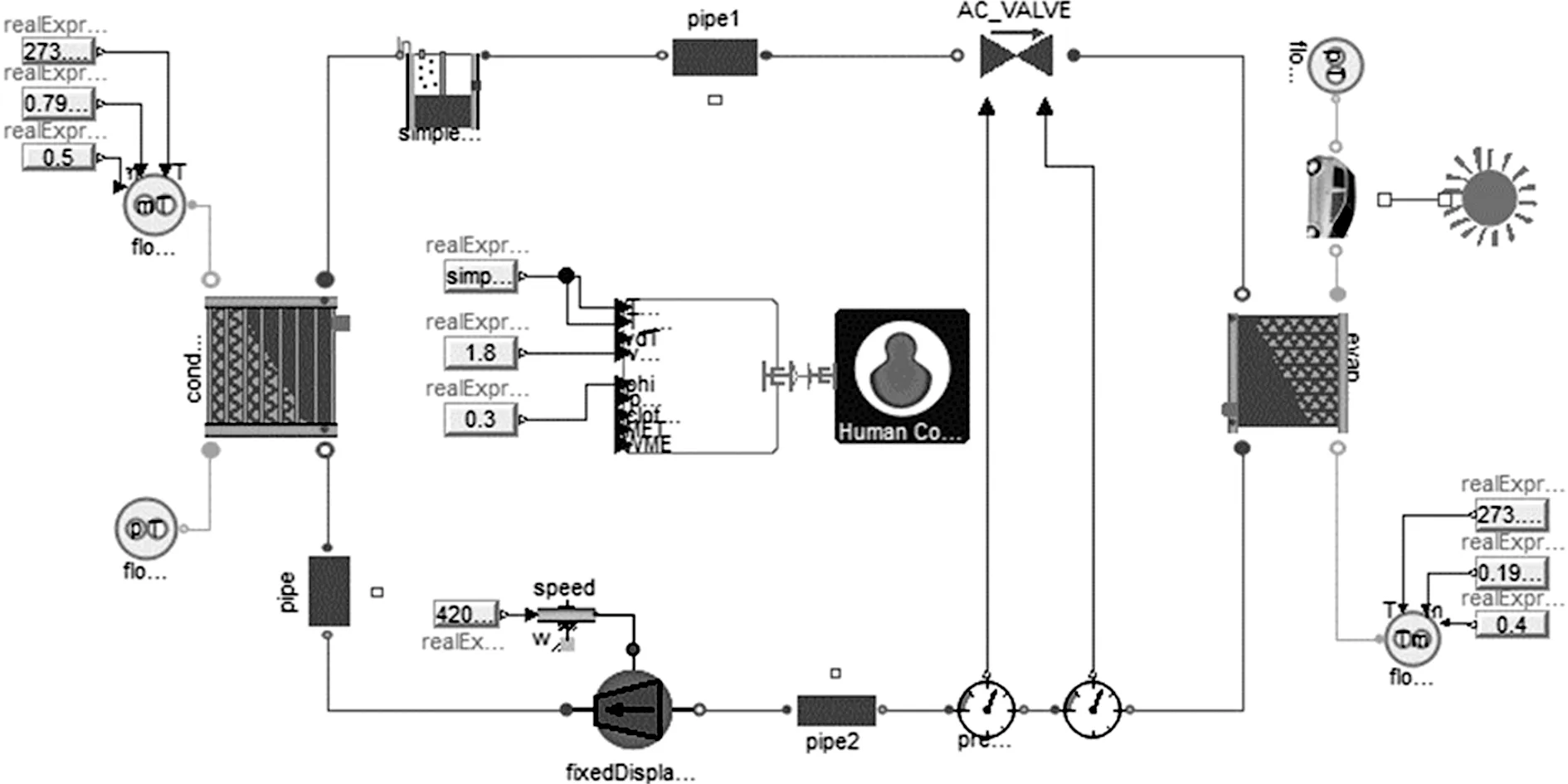
图3 空调系统模型
建立整车动力系统仿真模型如图4所示,主要包含以下模型或参数:驾驶行为模型和整车运行环境参数;发动机的动力输出、燃油消耗、启停控制、质量等关键参数;变速器的换挡逻辑、扭矩传递、质量等关键参数;制动系统的摩擦系数、制动力矩分配、制动踏板位置匹配、质量等关键参数;另外还包含车轮、车身、悬架、油箱等部件的固有属性参数。
图4 整车动力模型
2.2 多系统联合仿真模型
基于接口信息统一管理的理念,将上述3个一维模型进行集成。在各系统之间建立交互接口,通过创建信号传递总线来实现系统间接口耦合交互数据的统一管理。该模型可综合分析整车各工况下的水温、油耗、乘员舱舒适性以及百公里加速时间、最大速度等性能参数。集成模型如图5所示。
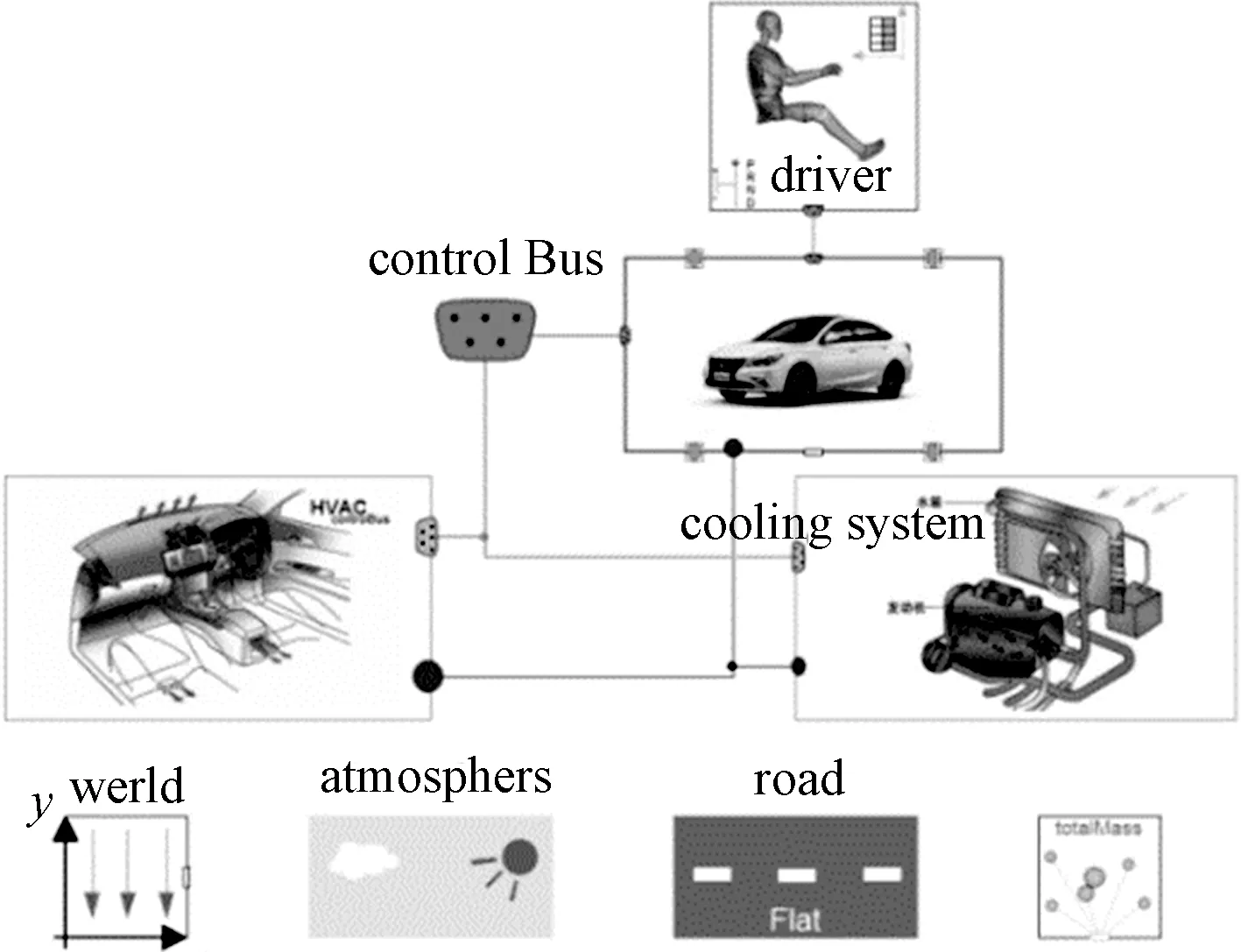
图5 多系统联合仿真模型
为了保证多系统联合仿真模型的精度,需要利用基础款车型数据进行标定,使得基础款车型在指定工况下的仿真结果与试验的误差较小,仿真结果如表1所示。

表1 基础方案联合仿真结果
3 多目标优化
基于选型的系统方案设计,首先是在给定部件型号的基础上将每个部件的型号与其部件参数进行对应,然后以部件型号为设计变量,寻找出满足优化目标的型号组合。
表2所示为某型号的水泵参数;表3所示为某型号的散热器参数;表4所示为压缩机参数。因各类部件型号较多,在此不一一列举。

表2 水泵P1参数
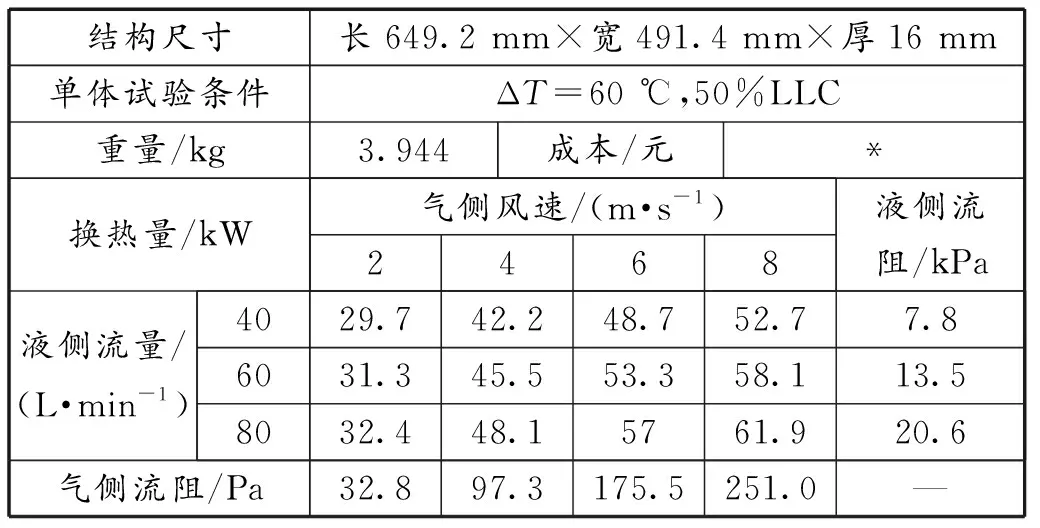
表3 散热器R1参数
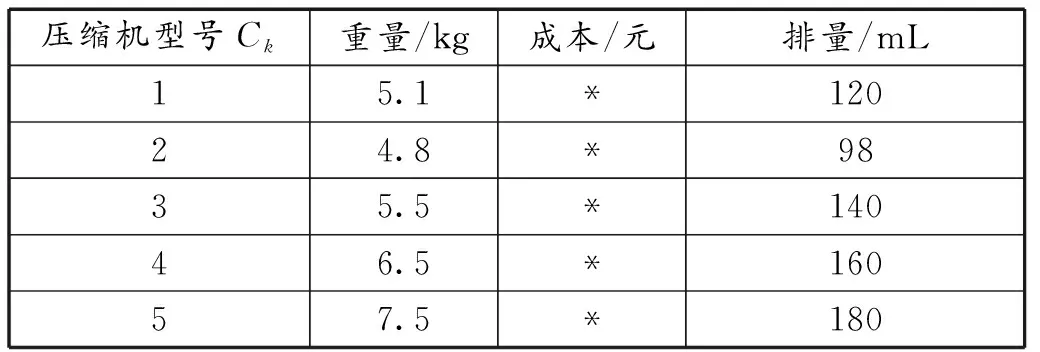
表4 压缩机Ck参数
由此,以散热器型号Ri、水泵型号为Pj、压缩机型号为Ck及风扇性能变化比例f为设计变量;以热舒适性PMV,乘员舱温度Tc、发动机出水温度Te、机油温度To为约束;以系统成本C最低、系统重量W最轻、油耗O最低以及最高车速Vmax最大为目标进行优化。建立优化模型如下:
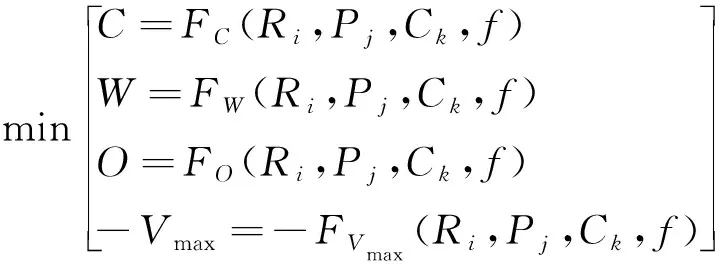
(1)
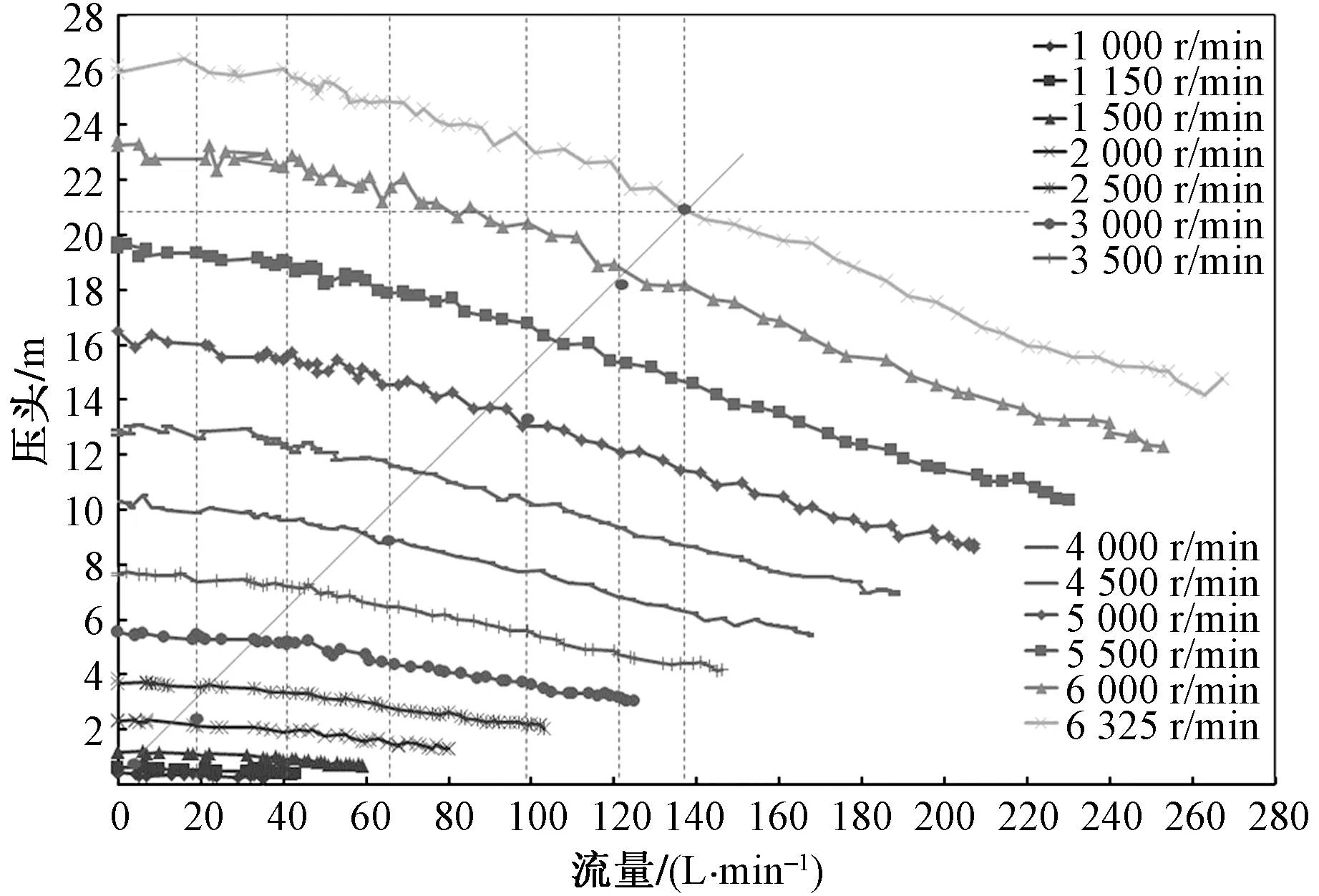
图6 水泵性能图
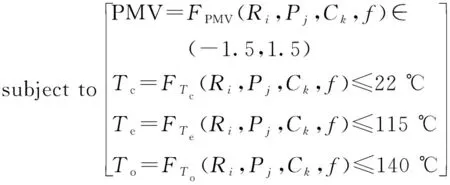
(2)
式中:i{1,2,3,4};j{1,2,3};k{1,2,3,4,5};f(0.9,1.1)。
基于Isight多学科优化平台,选用粒子群算法进行寻优求解,得到8个Pareto优化解,如表5所示。由表5可知,各方案在性能、成本、重量等方面各有优劣,但均满足设计约束。如何从方案集中决策出全局最优的方案,还需开展综合评价分析。
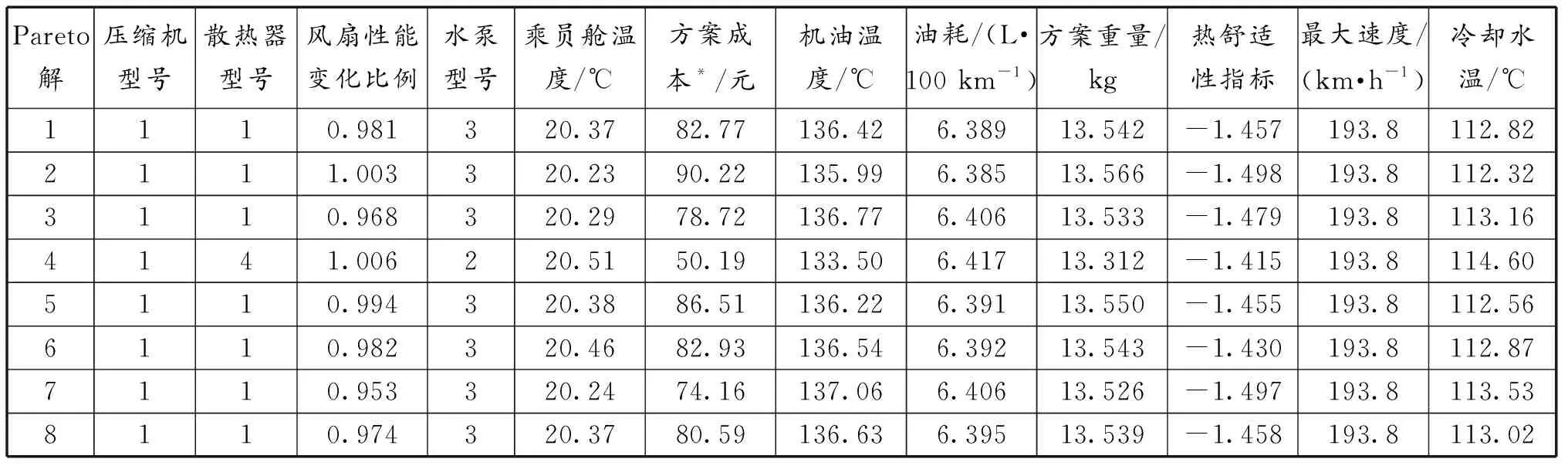
表5 Pareto方案集
4 综合评价
4.1 构建指标层次模型
采用层次分析法对Pareto方案集构建层次结构模型如图7所示。
第一层为最佳方案,即目标层。第二层包含舒适性、动力性、经济性,即准则层。该层次是实现所涉及的评价标准和影响评价的要素。第三层定义为指标层,该层次的各个指标分别由准则层分解得到。
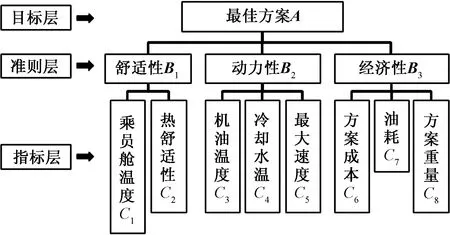
图7 层次结构模型
4.2 判断矩阵及权重计算
基于指标层次模型构建判断矩阵,设定目标层A与下一层次B中的要素B1、B2、…、Bn间产生联系,即可建立判断矩阵,如表6所示。
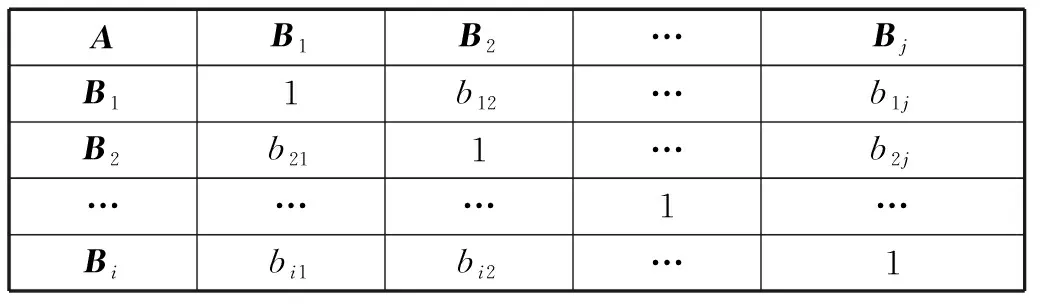
表6 判断矩阵构建形式
在确定各层不同因素相对于上一层各因素的重要性时,判断矩阵的标度可采用两个因素之间相互比较的方法,标度准则如表7所示。

表7 判断矩阵标度准则
根据判断矩阵,利用几何平均法对权重向量进行计算,计算步骤如下:
1) 计算判断矩阵M中每一行标度值的乘积Mi。
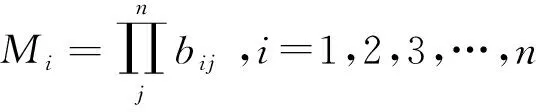
(3)
式中:bij表示判断矩阵中第i行第j列元素;n表示要素的个数。
2) 根据每行乘积Mi,计算判断矩阵各行元素的几何平均值ai。
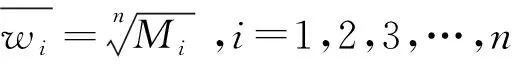
(4)
3) 进行归一化处理,计算指标层各个元素的相对权重wi。
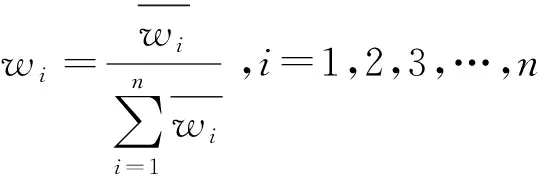
(5)
式中,w=(w1,w2,…,wn)T为所求得的权重特征向量,wi为w中第i行向量值。
结合产品定位和专家咨询,得到各层次的判断矩阵及权重如表8~表11所示。需要注意的是,基于Pareto方案集,各个方案的最大速度无差异,因此将其权重分配较低,但不影响整体评价结果。
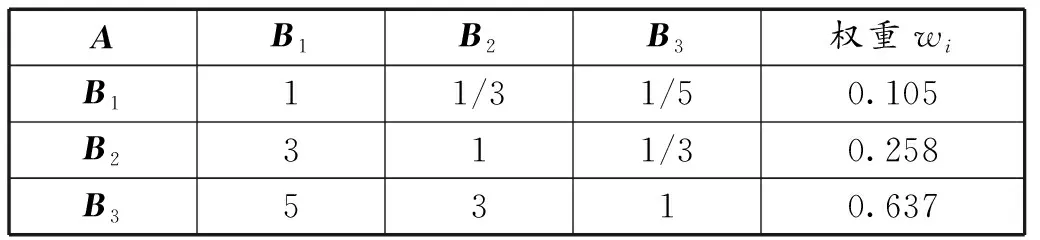
表8 最佳方案A的判断矩阵及权重

表9 舒适性B1的判断矩阵及权重
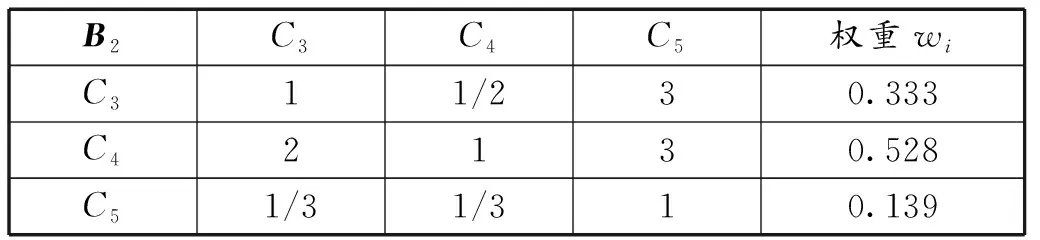
表10 动力性B2的判断矩阵及权重
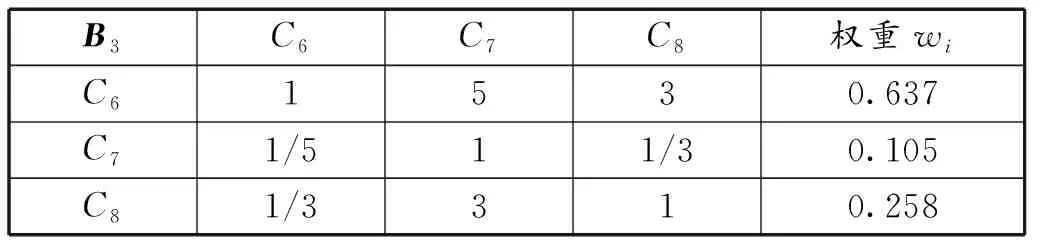
表11 经济性B3的判断矩阵及权重
4)一致性检验。为确保主观判断的一致性以及判断矩阵的相容性,需对判断矩阵进行一致性检验。用CI表示判断矩阵的一致性指标,用CR表示随机一致性比率,关系式为
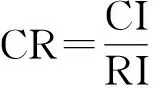
(6)
式中:
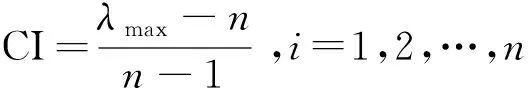
(7)
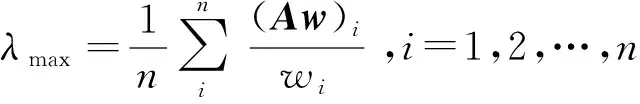
(8)
RI由平均随机一致性指标表查出,如表12所示。λmax为判断矩阵A的最大特征值;(Aw)i为向量Aw的第i个分量。当CR≤0.1时,认定判断矩阵的一致性可接受;反之,则需要修正判断矩阵后重新计算。

表12 平均随机一致性指标
基于上述方法,对目标层A和准则层B的判断矩阵进行一致性检验。结果为CR(A)=0.037、CR(B1)=0、CR(B2)=0、CR(B3)=0.037,均小于0.1,满足一致性检验要求。在各个判断矩阵满足一致性检验的基础上,将各层级的权重进行合成,得出总体排序,如表13所示。
4.3 综合评价
根据指标层各要素的权重计算结果,利用加权评分模型进行综合评分[19]。加权评分模型为
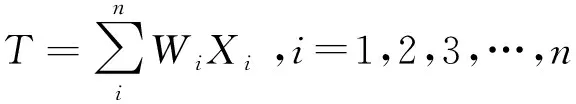
(9)
式中:T为某一评价对象的综合评价值;Wi为第i个评价指标的权重;Xi为第i个评价指标的评分值,可根据评分标准求得。
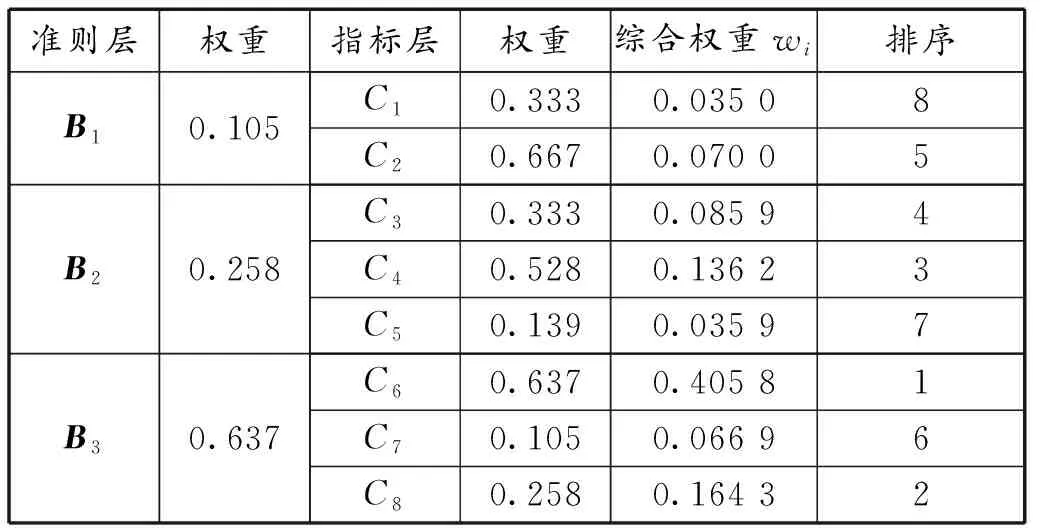
表13 指标层权重合成及排序
结合产品定位及专家咨询,构建指标层各属性的评分标准如表14所示。
基于评分标准,采用线性插值方法计算指标层Bi各属性对应方案的评分,结果如表15所示。根据指标层Bi的评分和权重,采用线性加权的方法计算目标层A的综合评分,结果如表16所示。
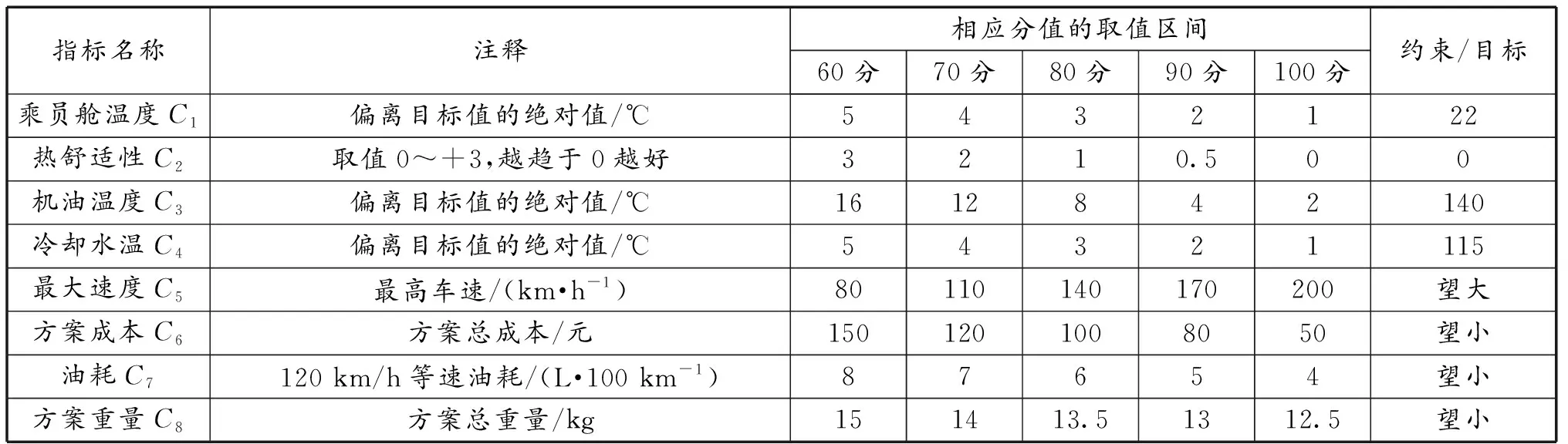
表14 评分标准
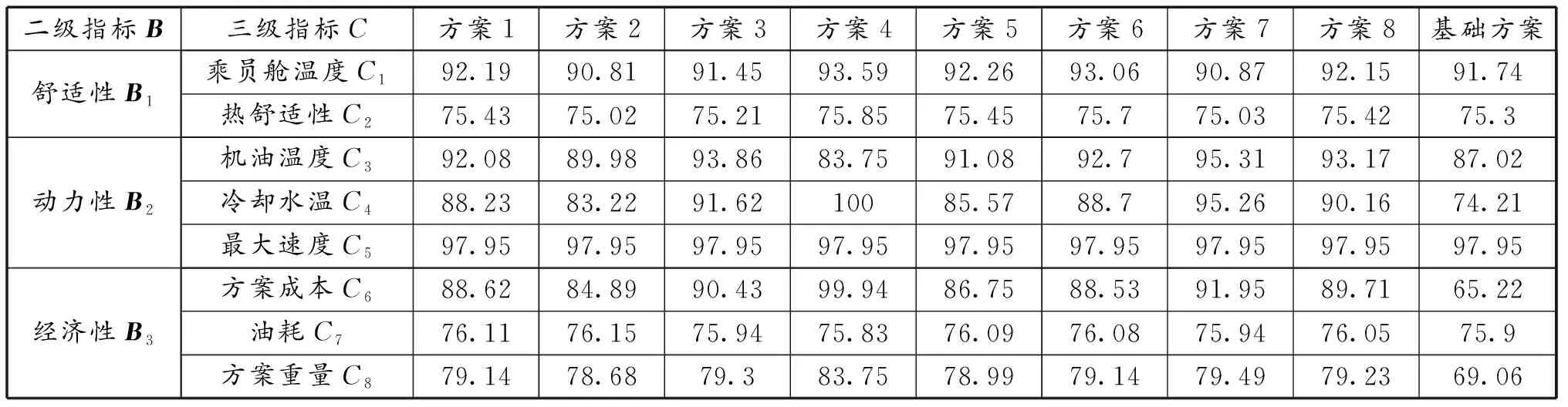
表15 各指标方案评分计算结果

表16 综合评分
由表16可知,方案4综合评价分值最高,为92.3分。基础方案综合评价得分为72.5分。Pareto解中的8个方案与基础方案相比,综合评价分值提升了15.2%~27.3%。
5 结论
针对当前汽车开发前期缺乏科学的方案决策的现状,提出了一种全面、客观、结构化的解决方法,包含多系统联合仿真、多目标优化及综合评价3个环节。基于此方法,以汽车整车热管理系统为对象,在一维多系统联合仿真和多目标优化的基础上,采用层次分析法和加权评分模型,对优化得到的Pareto方案集进行了综合评价。根据该方法得到如下结论:
1)系统综合评分值由基础方案的72.5分提升到了全局最优方案的92.3分,提升了27.3%。
2)评分最高方案虽然水温和油耗值相对有所上升,但成本和机油温度有所下降。由此可见,通过该方法,可定性和定量地选出满足开发需求的全局最优方案。
3)通过多系统联合仿真以及多学科优化,可减少在开发后期出现设计冲突、设计冗余等问题,从而减少后期整改;通过综合评价,可有效减少前期方案的评审时间,从而减少开发周期。
但是,该方法中提到的权重系数以及评分准则难以表征不同客户群体的主观感受。例如对于乘坐同一辆车的不同年龄段或者健康程度的群体而言,对温度的主观感受会有差异,从而使得热舒适性权重的分配模糊性较强。因此,在以后的实际开发过程中,还需加快解决该类问题。
