高炉炼铁含硅量的动态预测

万绍蒙， 李 劲

(昆明理工大学 管理与经济学院， 昆明 650093)

在流程工业中，钢铁冶金是具有代表性的国民经济支柱性产业，其生产过程非常复杂。要想对生产过程优化，关键是要将原来的反馈控制转换为预测控制，即通过大数据挖掘，确定生产过程的最佳途径与最佳参数控制范围，预测性地动态调整生产过程控制，获得最佳生产效果。以高炉炼铁为例，炼铁时所采集的工艺参数是一组高维的时间序列数据，影响高炉炼铁的质量数以百计。其终极生产指标产量、能耗、铁水质量等指标都与冶炼过程的一项控制性中间指标——炉温，即铁水含硅量(铁水含硅质量百分数)密切相关。对高炉炉温上升或下降的预测，即时间序列的预测关系着当前高炉各项操作参数的调控方向。

唐贤伦等[1]建立了高炉铁水硅含量预测模型，利用一种基于混沌粒子群优化(CPSO)的支持向量回归机(SVR)参数优化算法对实际数据进行求解，结果表明该算法有良好的预测效果。Srivastava等[2]提出了针对Corex工艺熔炉气化炉的热力学模型，在一定程度的直接还原铁(DRI)金属化过程中，模拟了Corex过程中热金属、炉渣和出口气体的组成。Srivastava等[3]提出了一种简单的相关性，以预测锅炉蒸汽中二氧化硅(SiO2)的溶解度与压力和水中二氧化硅含量的关系。将线性相关性预测与报告的数据进行比较，结果表明一致性良好，平均绝对偏差约为4%。Nurkkala等[4]提出了一种自动数据驱动的非线性模型生成算法，并将其运用到高炉炼铁中铁水硅含量的预测，该方法的缺点在于执行时间较长。李界家等[5]针对炼铁过程中硅含量检测滞后的问题，提出了集成模糊神经网络铁水硅含量预测方法，结果显示硅含量预测精度高。Saxen等[6]对研究高炉炼铁中硅含量预测问题进行了综述，总结了目前预测模型的准确性和原理，并给出了一些未来可能研究的方向。宋菁华等[7]提出基于经验模态分解(EMD)和Elman神经网络的铁水硅含量预测模型，来解决高炉连特过程中的动态问题。David等[8]通过建立人工神经网络数学模型来预测高炉炼铁过程中的硅含量，结果显示该模型有较好的精度。同时该模型还表面火焰温度吹气压力和焦炭率对铁水中硅含量具有正向影响。杨凯等[9]提出基于变邻域粒子群优化支持向量机的铁水硅含量预测模型，通过钢厂的实际生产数据进行验证，平均相对误差达到0.69%，模型具有很高的预测精度。庄田等[10]针对高炉炼铁过程中硅含量预测精度不高的问题，提出一种利用Elman-Adaboost强预测器实现硅含量预测的方法。该模型用于某钢厂硅含量的预测，其平均预测命中率达到了94.8%，证明了其有效性。李泽龙等[11]考虑到采集的数据具有前后关联性，采用LSTM-RNN模型进行硅含量预测。刘景艳等[12]针对传统神经网路在炉温预测中存在着收敛速度慢等问题，提出了一种基于小生境粒子群算法优化的径向基函数(RBF)神经网络预测模型。文冰洁等[13]利用BP神经网络建立了COREX铁水硅含量预测模型，通过相关分析法确定模型的输入参数，采用计算邓氏关联度的方式确定各参数对应的滞后炉次。Li等[14]提出了一种基于贝叶斯块结构稀疏的Takagi-Sugeno(T-S)模糊建模方法，利用该方法可以同时反映产品质量和高炉的热状态。尹林子等[15]提出基于粗糙集理论与神经网络模型对铁水硅含量进行预测，以国内某钢铁厂实际高炉生产数据进行验证，该方法在预测误差为±0.1%以内时预测命中率达到91.74%。罗世华等[16]利用偏态投影深度在数据有偏时可以较好地反映出数据离群情况的特点，将收集的数据进行分类，然后归类预测。

1 数据收集及处理

因为本文的数据采集都是由计算机完成的，所以在数据采集的过程中难免会录入一些虚假值，在使用采集的数据时需要对数据进行预处理。根据采集到的高炉数据的特点，为了保证数据处理的精度，针对异常数据的取舍问题，采用数据平滑滤波及数据归一化处理方法。

对于异常数据的判断采用格拉布斯检验法，即

(1)

(2)

(3)

式中：X表示采集得到的数据；μ为样本均值；S为样本标准差；Gn为统计量。

当确定水平α后，可通过查表得出相应的检验临界值。当计算出的统计量大于临界值时，则判断该数据为异常值，否则无异常值。

对于周期性噪声需要采用加权移动平均，即

(4)

式中：Δt为移动平均时间；C(t)为加权系数；n为进行加权移动平均的数据个数。

由于高炉参数数据之间数量级一般有一定差别，数量级大的数据会淹没数量级小的数据，因此在高炉炉热状态预报前必须进行数据标准化，即把输入变量标准化为之间的数据。对平滑滤波后的实时高炉数据进行如下处理：

(5)

式中，maxx和minx分别为变量x的最大值和最小值。

2 基于Elman神经网络预测模型

铁水含硅量与炉温密切相关，与其影响因子是非线性关系，利用传统的分析模型对其进行预测需要大量的专业知识，具有一定的难度。神经网络具有非线性逼近及自学习、自适应的能力，能克服使用传统预测模型过程中出现的某些困难，动态回归神经网络能够更好地反映系统的动态特性，文中利用Elman神经网络建立模型，并对铁水含硅量进行预测。

铁水含硅量与喷煤量、鼓风量、含硫量等因素有关。选取喷煤量、鼓风量、含硫量作为基于神经网络预测模型的输入。另外，考虑到铁水含硅量会随着时间的变化而变化，为提高预测的准确度，模型的输入还包括了历史数据及测量铁水含硅量时间。铁水含硅量在小范围内会有较大的随机性，因此，为了使模型的预测值不过分地依赖于历史实测数据，模型的历史数据输入只选取了过去两个炉次铁水含硅量实测值。模型可以表示为

(6)

2.1 改进型Elman神经网络算法

Elman神经网络一般具有两层神经元的动态递归神经网络，在BP网络基本结构的基础上通过储存内部状态使其具备映射动态特征的功能，从而使系统具有适应事变特性的能力，同时其隐含层神经元到输入层神经元之间还存在一个反馈连接通道，使得其自身具有检测和产生时变模式的能力。Elman神经网络模型与以往前馈神经网络算法相比较，其克服了训练速度较慢且无法达到全局最小及学习率的选择敏感等缺点，具有学习速度快、泛化性能好等优点，使得该方法模型已在许多领域得到研究和应用。Elman神经网络的结构如图1所示。

图1 Elman神经网络结构

2.1.1 改进型Elman网络基本结构

由于高炉冶铁是一个复杂的非线性过程，针对此问题，提出一种改进型Elman网络结构及算法。增加一个关联层，将隐含层的输出部分作为输入层的一部分，以达到储存网络的阈值和权值。改进型Elman网络结构图如图2所示。

图2 改进型Elman网络结构

分别为输入层到隐含层、隐含层到输出层、隐含层到关联层、关联层到隐含层的连接权矩阵，则该网络的动态方程可描述如下：

关联层的动态方程为

(7)

隐含层的动态方程为

(8)

输出层的动态方程为

(9)

式中：α、β为自反馈增益系数；f为隐含层的sigmoid函数。Elman网络采用的是BP算法进行权值修整，学习指标函数采用误差平方和函数，即

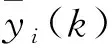
通过引入关联层来保证该网络的存储和记忆能力，并且可以通过调整α、β的数值达到网络对历史数据的记忆能力，从而增强网络的动态适应能力。

2.1.2 改进型Elman神经网络算法学习

通过图2可知，网络的隐含层输出及网络的输出反馈使得网络具有较强的记忆历史数据的能力。为了使网络的输出值更加贴近实际值，该网络采用的是动态递归算法来进行连接权调整。同时为避免Elman神经网络陷入局部极小值的情况，将在关联层引入附加动量来调整权值。附加动量法即将Elman网络算法的权值调整量加上部分上一次权值的调整量当作学习的权值调整量。其权值调整的公式为

ΔW(N+1)=Mc[W(N)-W(N-1)]-

(10)

式中：Mc表示加入的动量系数；N为训练的次数。

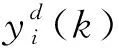
输入层到隐含层

(11)

隐含层到输出层

(12)

隐含层到关联层

(13)

关联层到隐含层

(14)

该网络的计算使用MATLAB软件来完成。在MATLAB软件中采用自适应学习速率的动量梯度下降反向传播算法来训练Elman神经网络。

2.2 案例计算

根据现有文献可知，铁水的硅含量与高炉炉温有着一定的关系。同时降低铁碎含硅量能够有效地改善钢铁其他各项生产指标，从而生产出优质钢，制造优质装备。通过查阅相关文献资料可知，含硅量[Si]与喷煤量PML、鼓风量FL、含硫量[S]具有非常显著的关系。

2.2.1 模型的训练及计算

从原始数据中用蒙特卡洛法随机抽取100个炉次的信息，组成100组数据样本作为仿真数据样本，将余下的数据样本用于神经网络的离线训练。在使用数据样本进行训练之前，为了加快神经网络的收敛速度，先对数据样本进行归一化处理。将处理后的数据导入到MATLAB软件中，在MATLAB中采用自适应学习速率的动量梯度下降反向传播算法训练Elman神经网络。将经过标准化处理后的喷煤量、鼓风量和含硫量作为网络的输入变量，则网络输入节点数为3。通过对网络的调节，当隐含层节点个数为20时，该网络可以较好地进行训练和预报。关联层节点个数等于隐含层节点个数，即为20。关联层2节点个数等于输出层节点个数，即为3。根据各层设置的节点可知，网络节点数目较少，网络结构比较简单。将设置好的节点数输入到MATLAB构建的模型中，导入数据。计算结果显示，改进型Elman神经网络迭代了295次之后，运算终止，训练效果达到最佳。神经网络模型对训练样本的拟合效果如图3所示。

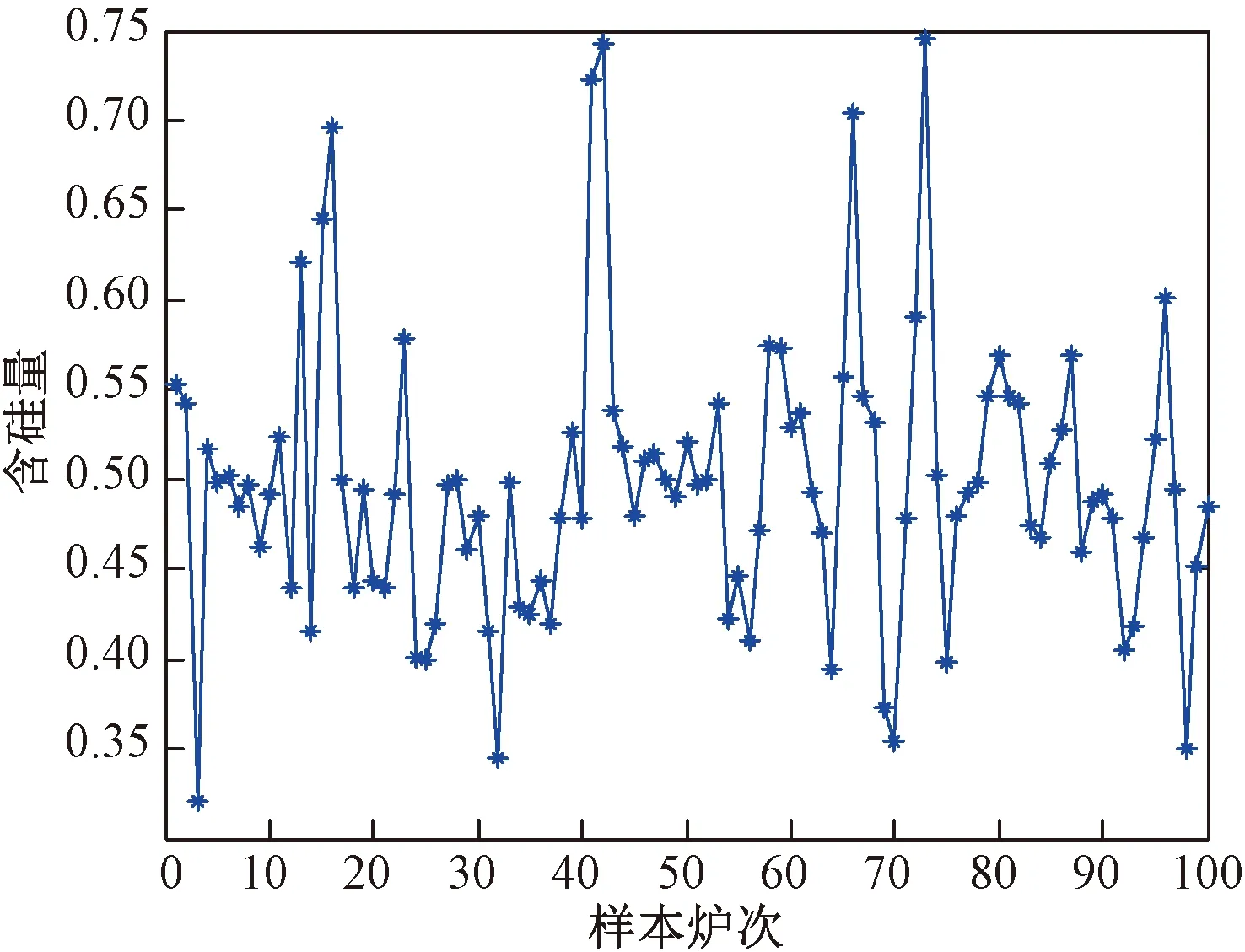
图3 训练样本模型输出值

2.2.2 预报成功率计算

通过对建立的铁水含硅量[Si]动态预测模型进行动态预测和仿真，可以得到预测数据和Elman神经网络训练性能，把实际数据与预测数据做图比较，其分别如图4和图5所示。

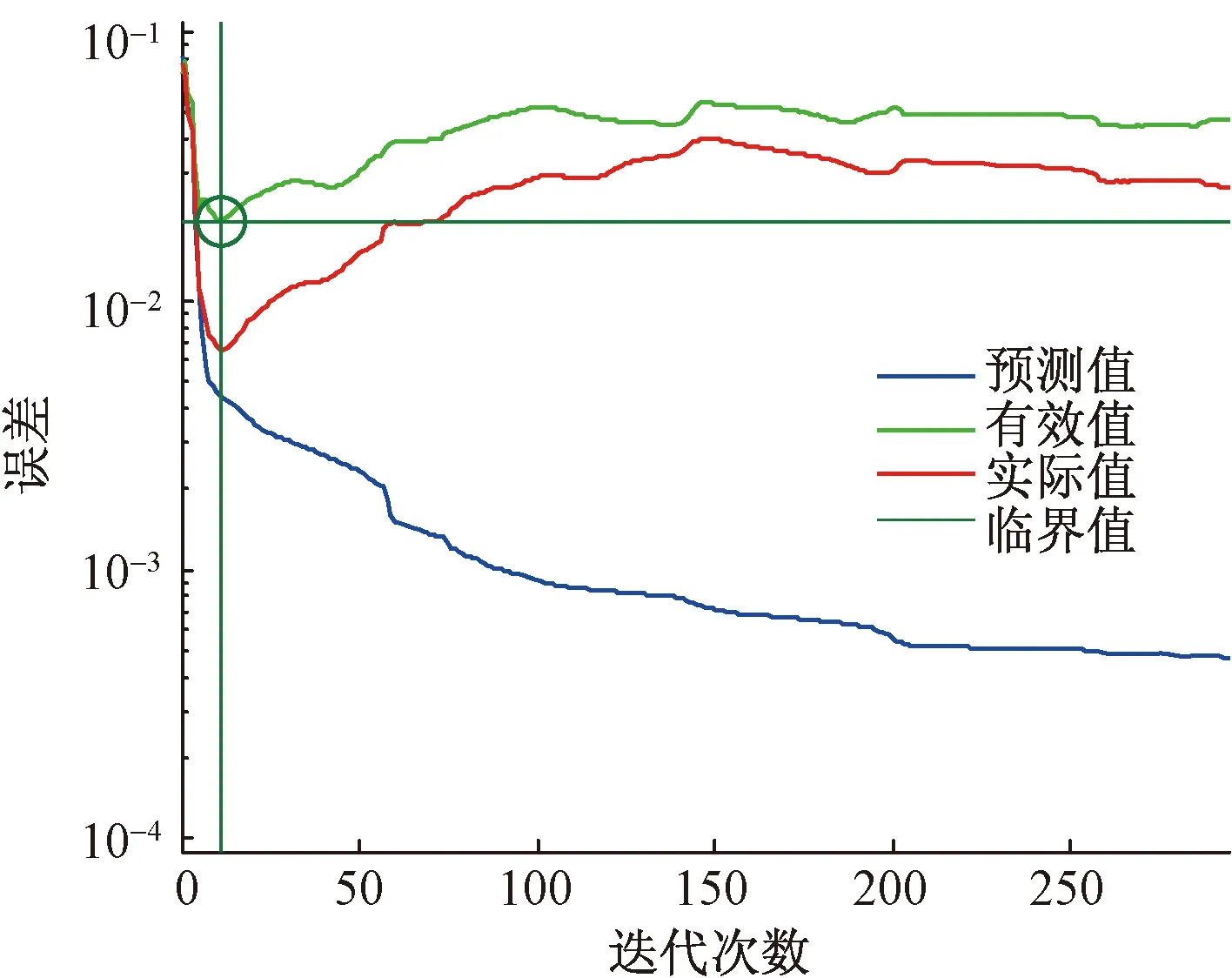
图4 Elman神经网络训练性能

从图4可以知道，当迭代11次的时候，Elman神经网络满足条件，其误差此时只有0.019 998，训练结束。改进后的Elman神经网络明显比标准的Elman神经网络迭代次数下降，误差减小。

图5 基于改进Elman网络模型的铁水含硅量预测值与实际值比较

通过图5预测值与实际值比较和图6的残差图可以直观地看出，以Elman神经网络模型为基础建立的铁水含硅量[Si]动态预测数学模型，绝对误差相差不大，有较好的预测和仿真能力。

图6 基于改进型Elman网络模型的铁水含硅量预测值与实际值残差图

在工程允许的误差范围下，对铁水含硅量预报的成功率通常用命中率来表示。假设预报得到的铁水含硅量为[Si]a，实际铁水含硅量为[Si]，两者差值为r=[Si]a-[Si]。如果r≤0.1，说明本次预报命中。一段时间内的命中成功率就是这段时间内所命中的炉数与总炉数的比值，用数学表达式表示为

(15)

式中：N(r≤0.1)表示预测命中的炉数；N表示预测样本总数。

表1给出了连续100炉高炉铁水含硅量预报结果的部分数据，以绝对误差不大于0.1统计，可得到预报命中率为90%。

表1 基于改进型Elman网络模型的铁水含硅量预测值与实际值

2.2.3 炉温升降方向预测成功率

铁水含硅量的升降方向的预测对冶金化工过程的控制具有十分重要的意义，采用残差分析法估计升降方向预测成功率，假设预报得到的铁水含硅量为[Si]a，实际铁水含硅量为[Si]，[Si]i为第i炉的铁水含硅量，则相应的实际炉温升降方向和预测的炉温升降方向可表示为

(16)

预测结果可表示为

(17)

式中，f=1表示预测成功，反之则为预测失败。

相应的预测成功率表示为

(18)

式中，N为预测样本总数。

表2为连续100炉样本铁水含硅量实际值与预测值的升降方向的部分数据，统计算出炉温升降方向预测成功率为92%。

2.2.4 预测控制结果的可信度分析

利用改进后的模型对采集的数据进行计算后可以看出，模型输出结果曲线和实际结果曲线之间的吻合程度较高，即模型有较好的预测能力。从这一方面考虑，该模型系统是可信的。为进一步检验模型的预测准确度，接来下对模型的预测结果进行可信度分析,采用统计检验法判断实验分析结果的可信度。

表2 连续100炉样本铁水含硅量升降方向

将随机选取的10炉铁水含硅量的实际值和模型预测的数值进行可信度检验。每个炉次的实际值和预报值如表3所示。

表3 铁水含硅量的实际值和预报值

运用统计量为

(19)

χ2的临界值可在资料中查到。当χ2>χ2(10,0.1)时，表明实际值与预测值存在显著性差异，即预测失败；反之，预测成功。由于计算复杂，利用SPSS软件进行统计量检验，其结果见表4。

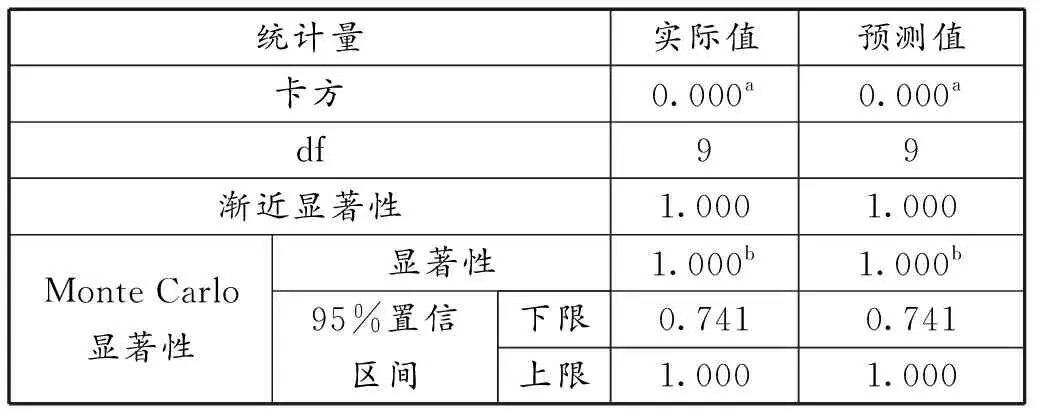
表4 统计量检验结果

从表4中可知，实际值与预测值之间的卡方值趋于0，且显著性值趋于1。根据资料显示，卡方值越小表示实际值与预测值之间越符合，显著性值越大则说明没有显著性差异。因此铁水含硅量预报的实际值和预测值无显著性差异，预报结果是可信的，同时也证明采用本文所建模型进行高炉铁水含硅量预测是可行的。

3 结论

高炉冶炼工艺是一个封闭、复杂的物理和化学过程，该过程具有非线性、滞后性等特点。要想保证生产的质量，就要保证高炉良好的热状态。特别在增加了辅助燃料喷吹和加湿鼓风等措施后，炉况的变化更加剧烈，对炉温的控制要求更复杂了。因此需要一种能对高炉炉热状态做出判断的方法，提前了解高炉的状态，就能及时的维持高炉稳定运行。

人工神经网络是一种基于连接主义机制的人工智能技术。它试图从微观上解决人类认知功能，以探索认知过程的微结构，同时在网络层次上模拟人类的思维方式和组织形式。人工神经网络模型具有非线性、适应性能力强、信息关联能力强、分析与设计具有一致性等优点。

基于人工神经网络模型的优点，建立了Elman神经网络模型来动态预测铁水硅含量，从而确定最佳生产效果。Elman神经网络是一种典型的部分反馈递归神经网络，它巧妙地通过关联层对系统的历史数据进行了有效的存储，从而在解决时序问题上具有相当的优势。Elman网络的动态特征仅是其内部连接提供，无须使用状态作为输入或训练信号，在解决预报问题时，Elman型人工神经网络具有动态特性好、逼近速度快、预测准确可靠等特点，而且Elman网络会对渐近递归计算得到网络的权值修正，从而进行实时预报。

通过建立的Elman神经网络模型，选择了合适的学习样本和验证样本，得到了铁水含硅量[Si]动态预测数学模型，获得了比较理想的预测成功率和炉温升降方向预测成功率，而预测成功率的提高，可以很好地减少和准确控制炼铁过程中的原材料用量，从而能够满足节能、优质、低耗、绿色环保等多目标要求，实现生产过程中的系统优化和智能控制，为流程工业的智能制造提供一定程度的参考作用。