基于机器学习的斜坡堤越浪量预测方法研究
2021-03-18胡原野王收军陈松贵
胡原野, 王收军, 陈松贵
(1.机电工程国家级实验教学示范中心(天津理工大学), 天津 300384; 2.交通运输部天津水运工程科学研究院 港口水工建筑技术国家工程实验室, 天津 300456)
防波堤是水工的重要建筑物,能够有效地防止水体越过堤顶,从而保护堤后建筑及人类活动的安全。越浪量是设计防波堤时考虑的一个重要参数,如果设计防波堤时能够计算出越浪量的大小,就能够在保证经济效益的同时,达到防波堤设计的要求,具有非常大的价值。因此,研究斜坡堤越浪量具有重要的意义。
随着社会的进步和计算机科学的发展,机器学习算法逐步进入人们的生活。机器学习是一种模仿人类学习过程的方法,在通过对大量数据的训练后,能够自动调整数据特征的权重或误差,寻求最优的学习规则,从而能够对新数据做出正确的判断,机器学习具有良好的预测能力。中外学者都曾采用机器学习方法预测越浪量。Medina等[1-2]以实验室中做的物理模型试验的结果作为模型的输入,建立了神经网络模型,并把神经网络模型的结果与观测值做了比较;Marcel等[3]通过集成学习方法计算了斜坡堤越浪量,并给出了模型预测结果的置信区间;Formentin等[4]对防波堤参数进行了进一步的研究,补充了模型的输入参数,从而改善了模型;liu等[5]将BP神经网络应用与珊瑚礁上的垂直海堤的越浪量;刘诗学等[6]将波高放缩为1,利用弗劳德相似准则对参数做无量纲化处理,对单坡式防波堤越浪量建立了集成神经网络模型;赵鑫[7]以深水波参数作为输入建立珊瑚礁地形上直立堤越浪量网络模型。
可以看出,对于越浪量的预测基本均是采用神经网络的方法,几乎没有其他机器学习方法。因此,本文针对斜坡堤越浪量,采用了3种不同的机器学习算法进行预测,分别为集成神经网络(ENN)、随机森林(RF)和支持向量回归机(SVR),并对3种算法的预测能力做了比较分析。首先介绍了数据的来源,并对数据做预处理,然后介绍了3种机器学习模型的原理及参数对模型的影响,最后介绍了相关的研究结论。
1 数据处理
1.1 数据来源
欧盟CLASH是由Delft大学开发的一个用于估算越浪量的工具。它搜集了世界上许多国家的越浪量实验数据,共计10 000多条,其中包括多种常见的防波堤类型。每条数据都包含波浪参数、防波堤参数和越浪量等。此外,数据中结构复杂性和实验可靠性分别用CF(complexity factor)和RF(reliability factor)表示,取值均为1~4。CF越大表明结构越复杂,RF越大则表明实验可靠性越低;反之,CF越小则结构越简单,RF越小则实验可靠性越高。
1.2 数据选择
由于机器学习算法的准确性与数据集有重要的关系,因此不准确或错误的数据会对模型产生较大的影响。需要对原始CALSH数据集做如下处理:删除结构复杂性最高(CF=4)和可靠性最低(RF=4)的数据;删除标签为Non-core的数据;为了模型的准确度,只保留q≥10-6m3/(s·m)(q为平均越浪量);此外,为了保证模型程序能正常运行,还需删除有缺失值的数据。
影响斜坡堤越浪量的因素十分复杂,难以考虑全部的因素。仅挑选出对斜坡堤越浪量影响较大的参数:堤前有效波高Hm0,t、堤前谱周期Tm-1,t、坡度m、波浪入射角β、堤前水深h、堤脚浸没水深ht、堤脚宽度Bt、平台以下结构与水平面正切值cotαd、波浪爬坡和下冲区(包括护堤)的平均角度的余切cotαincl、护面块体粗糙度γf、波浪爬坡和下冲区护面块体的平均粒径D、胸墙顶高程Rc、平台宽度B、平台上水深hb、堤顶高程Ac、肩台宽度Gc。斜坡堤结构示意图如图1所示。
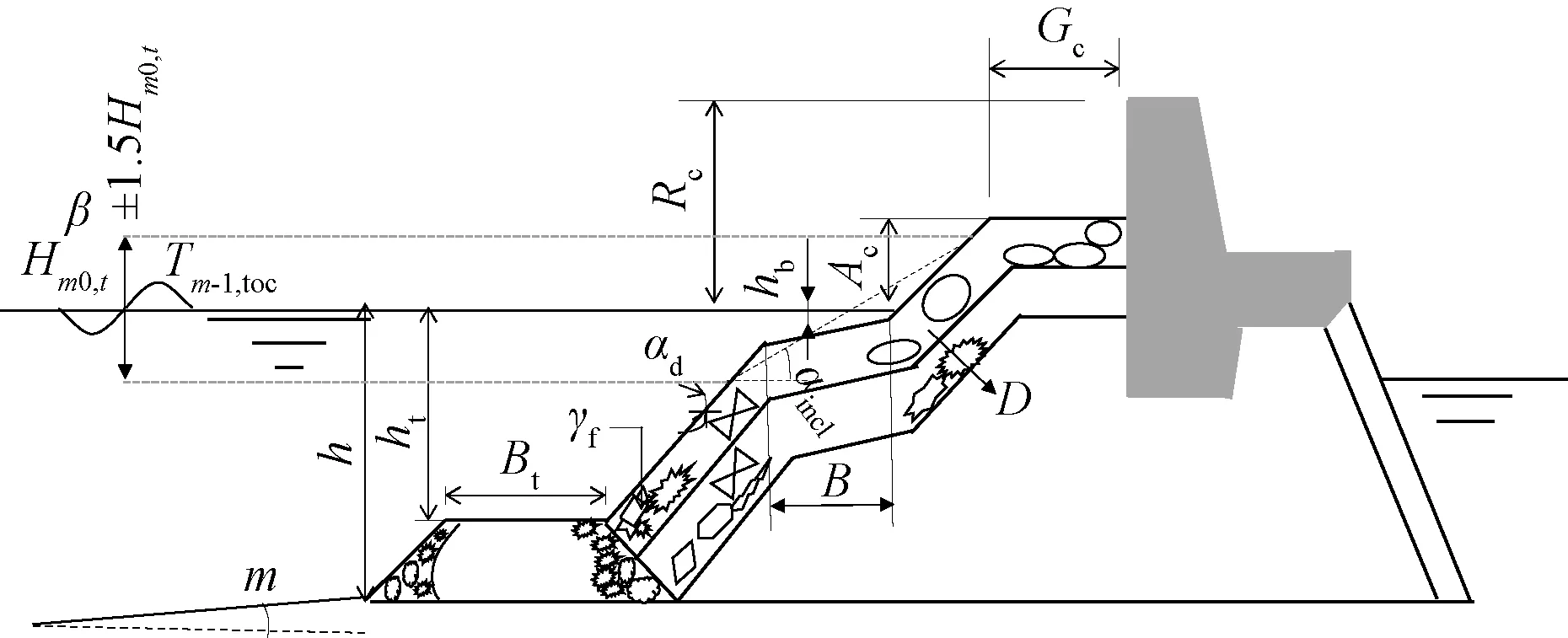
图1 斜坡堤示意图
1.3 无量纲化
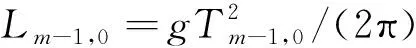
(1)
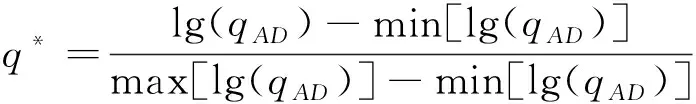
(2)
式中:q为越浪量,m3/(s·m);qAD为无量纲化后的越浪量,m3/(s·m);g为重力加速度,取9.8 m/s2;Hm,0,t为堤前有效波高,m;q*为归一化后的越浪量,m3/(s·m)。
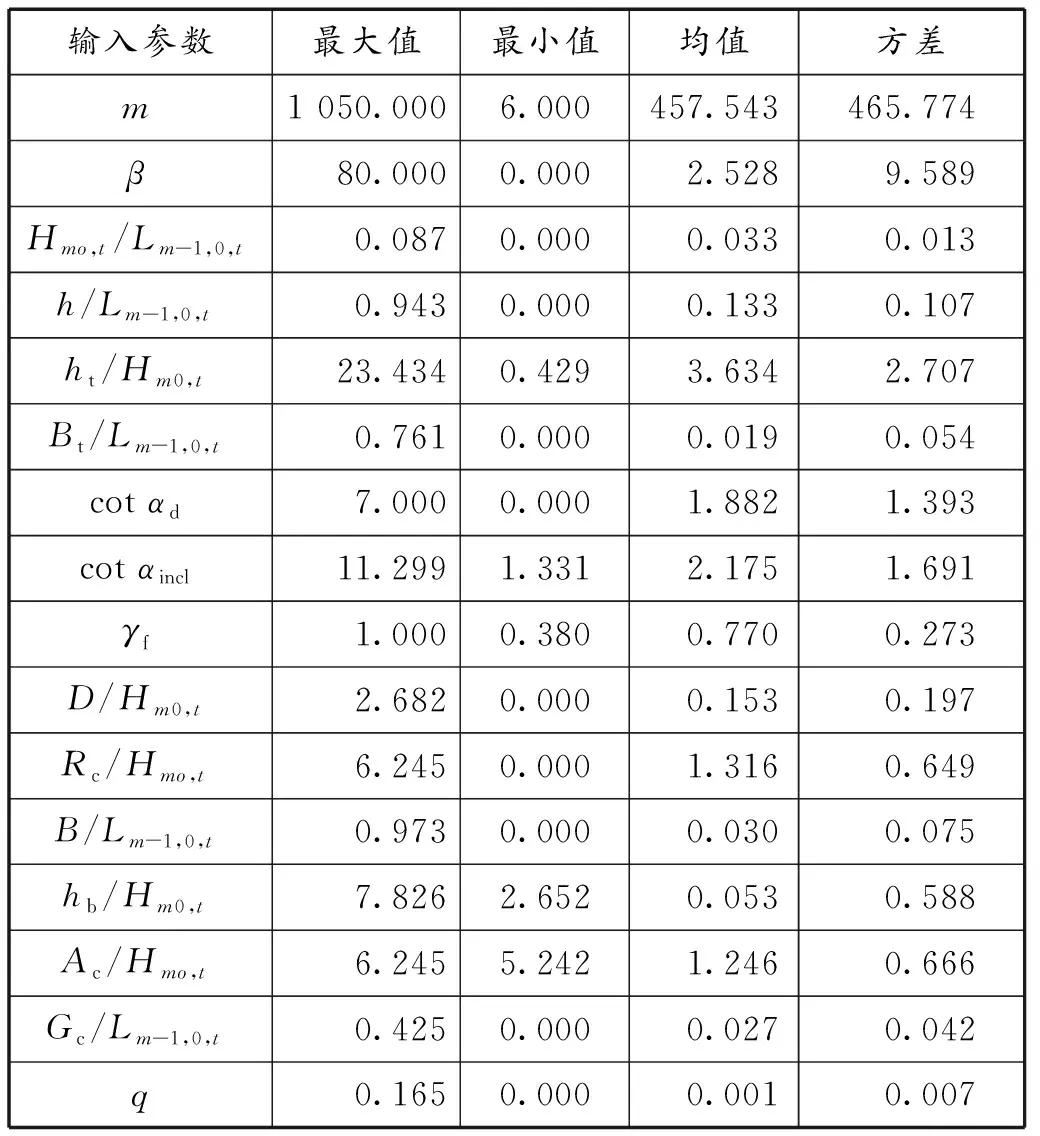
表1 无量纲化后各参数的分布
由于各个参数数值之间的差异比较大,不利于模型的训练,因此还需要对其做标准化处理,即将它们缩放到均值为0,方差为1。标准化方法为
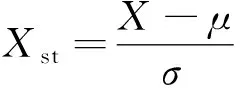
(3)
式中:Xst为标准化后的参数;X为原参数;μ为X上的均值;σ为X上的标准差。
2 斜坡堤越浪量预测方法
2.1 集成神经网络
2.1.1 神经网络
人工神经网络类似于人类大脑组织,由大量的神经元组成的网络结构,是人类大脑结构的简化和抽象[8]。人工神经网络模型包含输入层、隐含层和输出层。神经网络的训练过程就是把训练数据输入到网络中,经过每个特征的加权和及激活函数的映射,输出结果。将输出值与目标值之间的误差用损失函数Loss来表示,不断调整特征的权重ω和偏置θ,最终使得网络的损失函数Loss最小。
假设特征空间X=[x1,x2,…,xn],目标空间Y=[y1,y2,…,ym],权重ω=[ω1,ω2,…,ωn]T,网络的正向传播过程神经元的传播可以表示为
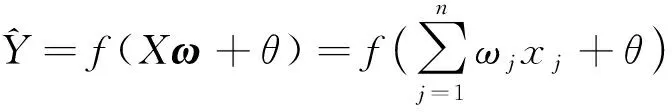
(4)
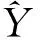
激活函数取双曲正切函数:
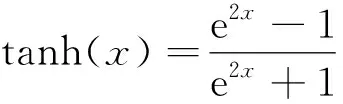
(5)
损失函数Loss选择均方差(MSE):
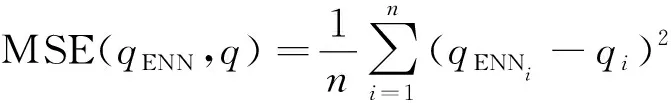
(6)
式中:qENN为神经网络的输出值;q为数据集中的实验值。
设置网络为一个隐含层,隐含层神经元个数直接影响神经网络的预测精度。图2为神经网络模型误差和隐含层神经元个数的关系,反映出了随着隐含层神经元个数的增加,网络误差减少,当神经元增加到50个时,网络误差最小;继续增加隐含层神经元个数,网络误差将增加,这是由于网络产生过拟合现象导致的。
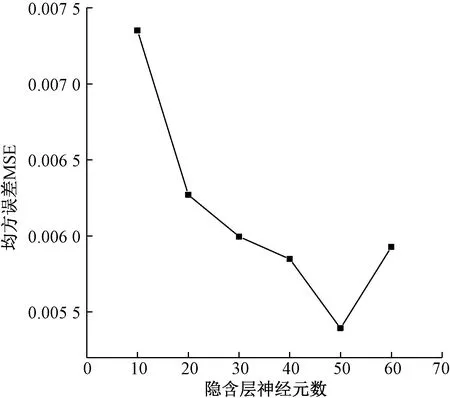
图2 隐含层神经元数对神经网络模型的影响
确定隐含层神经元个数为50个,建立的神经网络模型如图3所示。
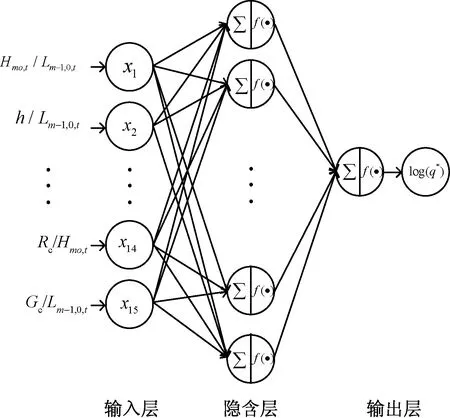
图3 神经网络模型
2.1.2 集成学习
集成学习是把多个学习器组合起来的一种学习方法[9]。一般地,集成学习模型要比单个学习器具有更好的拟合能力。对于集成神经网络模型,其原理是:在原样本集中随机有放回地抽取若干个子样本集,每个子样本集建立一个神经网络模型,通过某种策略将这些学习器组合起来。对于斜坡堤越浪量模型来说,随机抽取100个子样本集,建立100个子网络模型,最后采用平均法策略将这些子网络模型组成集成学习模型,即
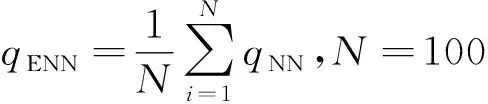
(7)
式中:N为子网络模型数;qNN为子网络模型的输出值;qENN为集成神经网络模型的输出值。
2.2 随机森林
随机森林是一种基于决策树模型的更为高级的算法,它的“随机性”体现在两个方面:①随机从原始样本中随机有放回地抽取若干子样本;②决策树中每个节点的分裂属性(特征选择)是随机确定的。“森林”体现在它是由许多个决策树组成的一个集成模型。两次“随机”保证了“森林”中决策树种类的多样性,从而使得随机森林的最终拟合效果高于单棵决策树[10]。
随机森林回归用于连续数据的拟合问题是由以特征为依据的最大化生长的多棵回归树构成的。由于随机森林的随机性,每棵树的数据集不完全相同,且每一次分裂时特征选择也不一样。每次分裂都遵循均方差最小原则。即对于特征空间X中任意特征x(j),对应的切分点s都会将训练集划分为区域R1和区域R2,定义R1(j,s)={x|x(j)≤s}和R2(j,s)={x|x(j)>s},寻求j和s,使得下式最小。
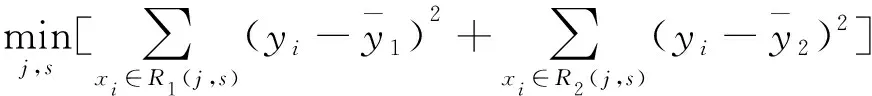
(8)
式中:yi为输出变量;
分别为区域R1和区域R2上yi的均值。
在确定最优的(j,s),节点就会分裂成两个子节点,对每个节点都重复以上过程,直至满足条件为止。
影响随机森林模型性能的参数有许多,这里,主要对其中影响较大的两个参数进行选择:随机森林模型中决策树的数量(n_estimators)和树的最大深度(max_depth),其他参数选择Python中Sklearn库的默认值。参数n_estiomators和参数max_depth采用网格搜索(GridSearchCV)的方法进行遍历,寻求最优的组合。图4为建立随机森林模型时的误差与决策树个数和树的最大深度的关系,反映出随着决策树数量的增加,随机森林模型的误差逐渐减小,当减小到某值时,即使再增加决策树数量,误差也不再减小。但决策树数量越多,模型训练的所需的时间越长,就需要消耗更多的计算资源;随着每棵决策树的分裂的最大深度越大,决策树结构也就越复杂,随机森林的误差也越小,进一步增加树的最大深度,随机森林误差也没有出现再增加的现象,这表明随机森林模型不易出现过拟合现象。
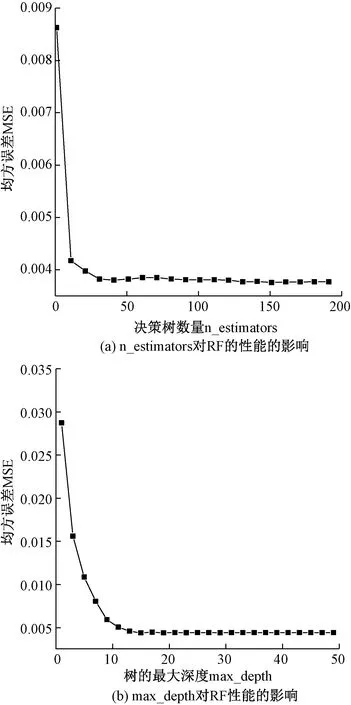
图4 决策树数量和树的最大深度对随机森林模型的影响
2.3 支持向量回归机
支持向量机(SVM)是在统计学习理论基础上发展起来的基于结构风险最小化原则的机器学习理论,根据有限的样本信息在对特定训练样本的学习精度和学习能力之间寻求最佳折中,以获得最好的泛化能力[11]。
支持向量回归机是支持向量机在回归问题上的一种方法。原理是:寻找一个超平面去拟合样本数据中所有的样本点,使得样本点离超平面的总偏差最小。对于线性可分问题,设数据集D={(x1,y1),(x2,y2),…,(xm,ym)},目的是希望学习到一个线性回归方程式(5),使得f(x)和y尽可能地接近。
f(x)=ωTx+b
(9)
式中,ω和b为模型参数。此外,SVR模型可以允许f(x)和y之间有ε的误差,且在f(x)和y之差的绝对值小于ε不计算损失。SVR模型图5所示,超平面参数完全由A、B、C3个点确定,这3个点被称为支持向量。
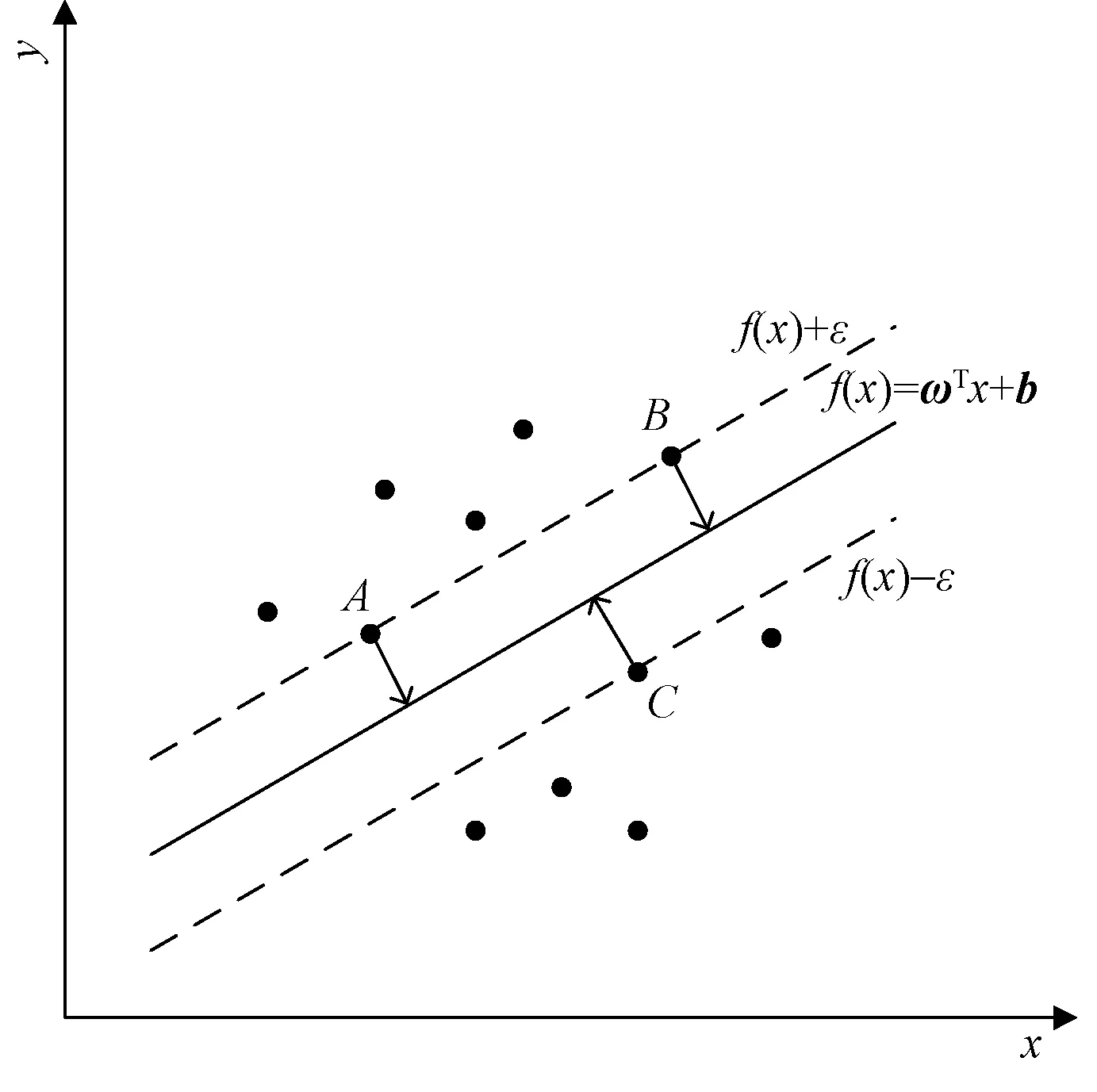
图5 SVR模型图
对于低维空间中线性不可分样本集,通过核函数将其映射到高维空间中,使其线性可分,常见的核函数:线性核(Linear Kernel),多项式核(Polynomial Kernel),径向基核(RBF Kernel),卡方核(Chi-squared Kernel)等。选取径向基核,因为径向基核能够实现线性到非线性的映射。其表达式为
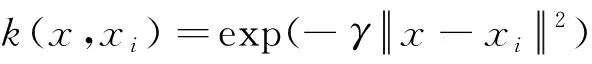
(10)
式中:xi为输入向量;γ为径向基函数参数,x∈Rn。
在支持向量回归机模型中,对模型的预测精度影响较大的参数是惩罚参数C和径向基函数参数γ。惩罚参数C表示SVR模型对误差的容忍性,C越大,说明越不能容忍出现误差,容易出现过拟合,C越小,则模型容易出现欠拟合,不管C过大还是过小,都会使SVR模型的泛化能力变差。径向基函数γ决定了映射后的特征空间分布,γ值越小,支持向量越多,γ值越大,支持向量越少,支持向量的数量影响着SVR 的训练速度,支持向量越多,训练速度越慢,反之,训练速度越快。图6为建立模型时的误差与惩罚参数C和径向基函数参数γ的关系,反映了SVR误差随着C和γ均呈现出先减小后增大的趋势。
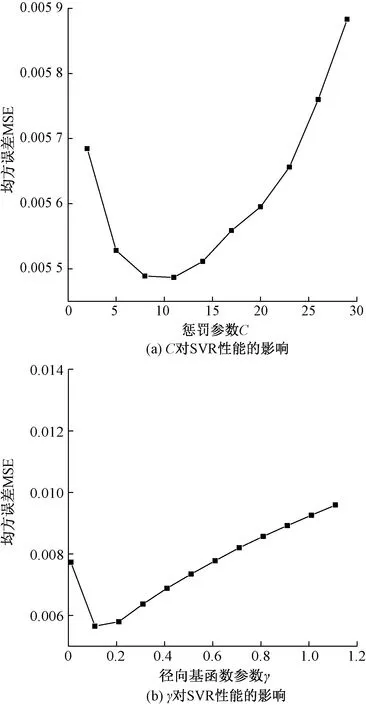
图6 惩罚参数和径向基函数参数对支持向量回归机模型的影响
2.4 模型建立及评估指标
基于Python编程语言,以影响越浪量的15个参数作为输入,平均越浪量作为输出,建立基于机器学习方法的越浪量预测模型,并将预测结果和数据集中实验值进行验证。将数据集划分为训练集和测试集,其中,训练集占90%,用于训练模型;测试集占10%,用于评估模型的预测能力。
为了评估ENN、RF和SVR 3种机器学习模型对斜坡堤越浪量的预测能力,本文选择决定系数(R2)和均方根误差(RMSE)作为评估指标。决定系数(R2)表明了预测值与真实值的密切程度,R2越接近1,说明越密切;反之,说明越离散;均方根误差体现了预测值与真实值的误差,RMSE越大,说明模型的性能越差,反之,RMSE越小,则说明模型的性能越好。公式表示为
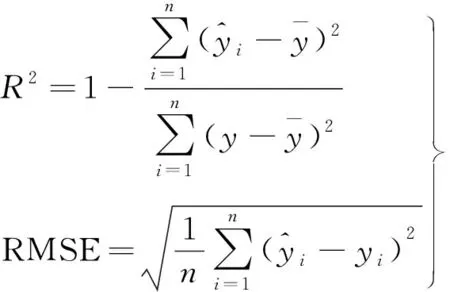
(11)
3 结果分析
3.1 模型的预测结果分析
将测试集分别输入到ENN、RF和SVR 3个模型中,并计算出3种模型在测试集上的R2和RMSE值。结果见表2。
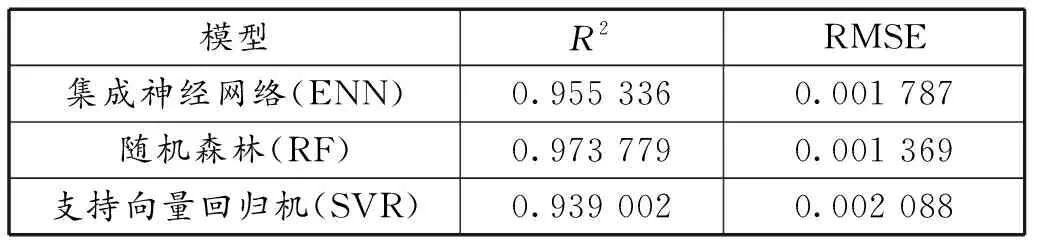
表2 3种机器学习模型评价表
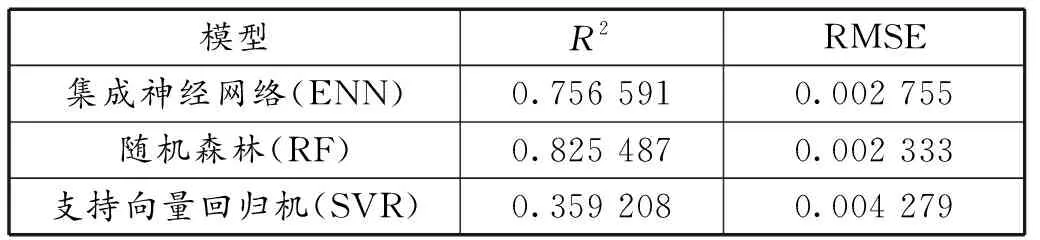
表2说明对于斜坡堤越浪量的3种机器学习模型,R2:RF>ENN>SVR;RMSE:RF 图7 3种机器学习模型在测试集上的预测结果 图7为3种模型在测试集上的预测结果,横坐标为数据集中的实验值,纵坐标为3种模型的预测值,两侧的虚线为5倍公差范围,中间的虚线为45°理想线。可以看出,当越浪量在10-6≤q<10-4范围内时,3种模型均有较多的点落在了5倍公差范围之外,可能的原因是数据集本身的不准确造成的;当越浪量在10-4≤q≤10-3范围内时,SVR模型和ENN模型均有一些落在5倍公差范围外,而RF模型的所有预测点均落在5倍公差范围内,说明在此范围内,RF模型的预测结果优于其他两种模型;当越浪量在10-3 为了验证训练集对斜坡堤越浪量模型精度的影响,对训练集不做数据选择处理,建立ENN、RF和SVR 3种模型,测试集上的R2和RMSE如表3所示。 表3 3种机器学习模型评价表(不做数据选择处理) 由表2和表3得到,如果不对数据进行处理,ENN、RF和SVR 3种模型的R2值分别降低了0.198 745、0.148 292、0.579 794;RMSE值分别增加了0.000 968、0.000 964、0.002 191。说明3种机器学习模型的预测精度均受到训练集的影响,而SVR模型对数据噪点较敏感,它的预测精度下降最为明显。 训练集中会存在一些有缺失值、不准确甚至错误的信息,这些信息都会在模型训练中产生一定的影响,从而使得机器学习模型的预测结果出现较大的偏差。因此,对训练集进行数据处理能够显著提高机器学习模型的预测精度。 1)利用欧洲CLASH越浪数据集分别建立了集成神经网络、随机森林和支持向量回归机3种机器学习模型对斜坡堤越浪量进行预测研究,并对模型参数如何影响模型误差做了分析,最后将3种模型的预测结果进行对比分析。 2)随机森林由于内在的随机性算法使得模型不产生过拟合现象,模型的误差为0.001 369,预测结果决定系数达到0.97以上;集成神经网络采用集成学习方法,其误差为0.001 787,预测结果决定系数达到0.95以上;支持向量回归机是一种独立的算法,建模简单,模型计算速度快,其误差为 0.002 088,预测结果决定系数达到0.93以上。3种机器学习模型的决定系数均能达到0.9以上,说明3种模型对斜坡堤越浪量均具有较高的预测精度,相比之下,随机森林的预测结果更为可靠。 3)机器学习算法的预测结果不仅与自身算法有关,还受到训练集影响。因为模型的建立和训练均是依据训练集的准确性及数据分布。因此,补充正确的越浪量数据,有助于进一步提升模型精度。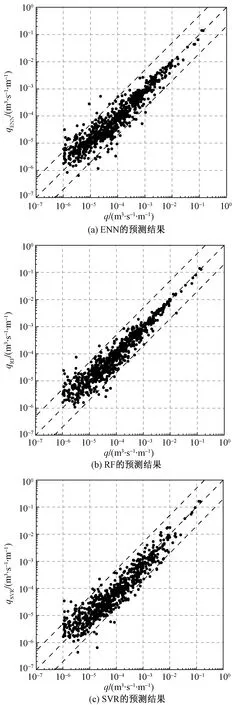
3.2 训练集对模型的影响
4 结论
