模糊需求下低碳取送货车辆调度问题与算法
2021-03-18*
*
(1.河北工业大学经济管理学院,天津 300401;2.河北工业大学财务处,天津 300401)
0 引言
随着社会经济的飞速发展,温室气体排放量急剧增加,环境污染问题引起了全球各国的高度重视。物流运输行业作为一个高能源依赖行业,据相关统计,碳排放量占全球总排放量18%。在国家大力推行节能减排的背景下,合理的配送路径规划不仅可以帮助企业有效降低物流运输成本,而且有利于降低运输过程中的能源消耗,从而减少碳排放量,带来更好的环境效益和经济效益。
近几年,低碳车辆调度问题逐渐受到各领域专家和学者的关注。何东东等[1]引入碳排放量和油耗的近似计算方法,建立成本最小化的带时间窗多车型绿色车辆调度问题(Green Multi-type Vehicle Routing Problem with Time Window,G-MVRPTW)模型。唐慧玲等[2]研究带有碳排放约束的车辆调度问题,构建车辆行驶路径最短和碳排放量最小的多目标函数模型,并采用改进的蚁群算法求解模型。张明伟等[3]针对车辆在配送过程中产生大量碳排放问题,建立碳排放量最小、服务时间最短以及行驶路程最小的多目标模型。周鲜成等[4]针对时间依赖型绿色路径问题,构建车辆碳排放成本、油耗成本、车辆使用时间成本和人力成本、固定发车费用等成本之和最小的时间依赖型绿色车辆调度(Time-Dependent Green Vehicle Routing Problem,TDGVRP)模型。葛显龙等[5]考虑国家节能减排号召,对车辆调度问题进行研究,建立碳排放成本和旅行成本最小化和配送时间最小化的双目标模型。赵志学等[6]从绿色环保角度出发,建立车辆油耗和碳排放总成本最小和车辆运营总成本最小化的绿色车辆调度(Green Vehicle Routing Problem,GVRP)双目标函数模型,并采用混合差分进化算法求解该模型。葛显龙等[7]建立以车辆数最少、碳排放量最小和行驶距离最短为目标的开放式污染路径(Open Pollution Routing Problem,OPRP)数学模型,采用改进的遗传算法求解。Maden 等[8]使用启发式算法求解带时间窗车辆调度问题(Vehicle Routing Problem with Time Window,VRPTW)模型,使CO2排放减少7%。Tajik 等[9]考虑燃料消耗,以行驶距离和车辆数最小化为目标,构建带时间窗同时取送货污染路径问题(Time Window Pickup-Delivery Pollution Routing Problem,TWPDPRP)数学模型。
综上,总结近几年相关研究,见表1,可以得到现有车辆调度相关文献,对问题中存在的模糊需求、碳排放和同时取送货等特性,仅考虑了其中一个或两个,少有文献将这些问题特性综合考虑。同时,现有文献在研究低碳配送问题方面,多数将碳排放问题转化为成本的一部分,建立总成本最小的单目标模型。基于此,在考虑模糊需求、碳排放和同时取送货的情况下,探讨更为科学的低碳目标设置,即构建三个模型,模型一以运输成本最小为目标函数、模型二以碳排放量最小为目标函数、模型三以运输成本和碳排放成本构成的总成本最小为目标函数,同时分别记录三种情况下的运输成本和碳排放量,对三种模型的结果进行分析和比较。最后,提出基于2-OPT(2-OPTimization)的差分算法求解,以提高算法求解效率。
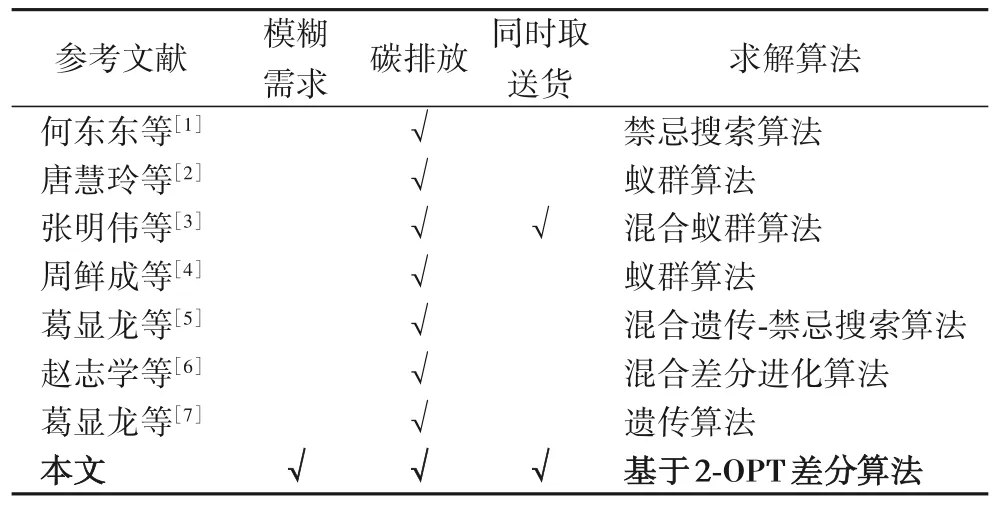
表1 关键文献总结Tab.1 Summary of key literatures
1 问题描述及模型建立
对模糊需求和低碳同时取送货问题的描述如下:整个配送网络有一个配送中心,使用同一型号车辆对客户进行配送作业,同时满足各客户的取送需求。在配送过程中,配送车辆需从配送中心出发,最终回到配送中心,且无论何时何地,配送载量不能超过车辆自身的最大载重量。模型中,考虑顾客的模糊需求和同时取送货问题。分别建立以车辆运输成本最小化、碳排放量最小化、以运输成本和碳排放成本构成的综合总成本最小的三个模型,研究三种不同目标下的同时取送货数学模型。
1.1 期望模糊需求
近几年,部分学者开始使用模糊理论描述车辆调度中的不确定因素。Heilpern[10]于1992 年提出模糊数概念,引入期望区间和模糊数期望值的概念。三角模糊数为解决不确定环境下的问题提供了理论基础,避免了理论数量上的“固化”,使研究更能适应于生活中的灵活性和随机变动性。张莉等[11]针对易腐食品供应链研究,因需求不确定加大了决策者的决策难度,利用三角模糊数处理外部的不确定需求,从而构建零售商决策模型。马艳芳等[12]引入三角模糊数描述客户需求的不确定性,建立运营成本、油耗成本和碳排放的总成本最小化为目标函数。Brito 等[13]认为行车时间和顾客需求是不确定的,并将其处理为模糊约束。
在生活中,由于各种不确定因素,在收集客户需求信息时,只能获取一个模糊的数据,而这些数据大多经验所得,如“此次需求在1 至4 吨之间,最有可能的值是2.7 吨”。针对该种情况,将需求处理为模糊需求,那么将1、2.7和4分别作为三角模糊数的左边界(即α)、中间值(即γ)和右边界(即β),构成三角模糊数η=(α,γ,β),其中0 <α≤γ≤β,其隶属函数[10]为:

其中:α、β分别为三角模糊数的下限和上限,γ为三角模糊数最有可能的取值。
假设Z是边fZ和gZ的模糊数η=(α,γ,β),可以得到:
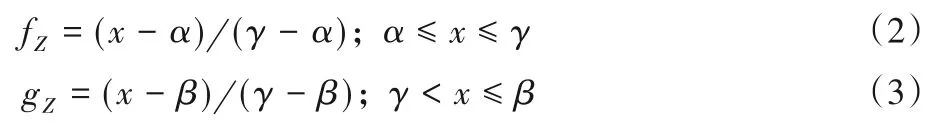
定理1[10]区间随机集S~RI(Z)的期望值称为模糊数Z的期望区间,用EI(Z)表示:

其中:

定理2[10]模糊成员Z的期望区间中心称为该数的期望值,用EV(Z)表示,则有:

用一个简单例子说明,令Z=η(1,2.7,4),则有:

根据定理1和定理2得到:

进而求得,EI(Z)=[1.85,3.35],EV(Z)=2.6。基于以上理论,可以获取三角模糊数的期望值。
1.2 碳排放计算
在现实生活中,影响运输碳排放量的因素众多,如运输车辆的载重量、行驶的距离、路况、车型和行驶速度等。本文采用文献[14]碳排放计算方法,碳排放主要包含:运输的货物产生的二氧化碳和运输车辆在运输过程中自身产生的二氧化碳。具体公式如下:
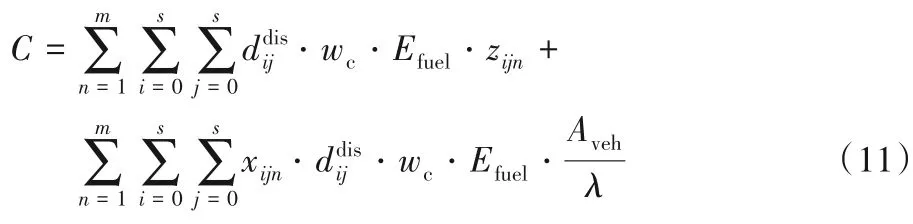
各参数取值具体如表2所示。

表2 碳排放计算相关参数Tab.2 Relevant parameters of carbon emission calculation
1.3 模型构建
模型构建所需符号如下:
Qn为车辆最大载重量;
zijn为车辆n从客户i点到客户j点的装载量;
zi为车辆离开i点时的装载量;
N为车辆的集合,N={1,2,…,m},m为最大可用车辆数;
S为节点集合,S={i|i=1,2,…,s};其中i=0 表示物流中心,i=1,2,…,s表示客户;
cn为车辆n行驶每公里的成本,其为变动成本;
cc为每千克二氧化碳排放费用;
W为车辆运输成本;
C为总碳排放量;
Z为配送总成本。
基于以上理论,建立三种目标下的低碳取送货问题模型。模型一以运输成本最小为目标函数,如下:
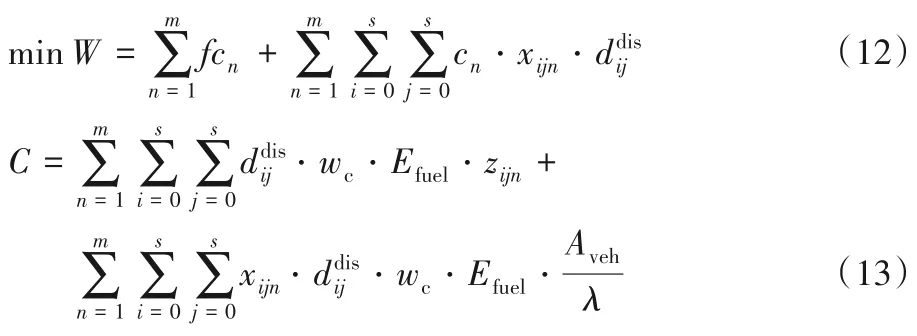
式(12)为模型一的目标函数,表示运输成本最小化,成本共包括两部分,一是运输车辆的固定成本,二是运输车辆与距离相关的变动成本。式(13)表示该模型下相应的碳排放量。
模型二以碳排放量最小为目标函数,模型如下:
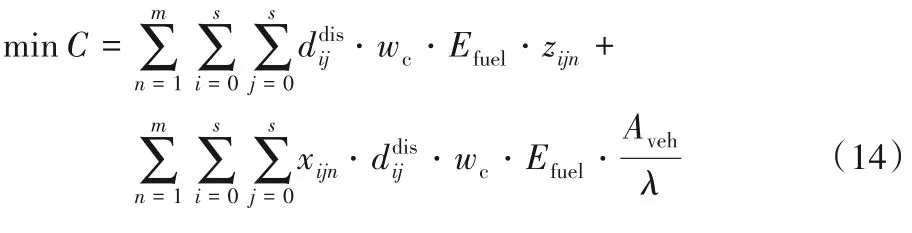

式(14)为模型二的目标函数,表示碳排放量最小化;式(15)表示该模型下相应的运输成本。
模型三以运输成本和碳排放成本构成的综合总成本最小为目标函数,模型如下:
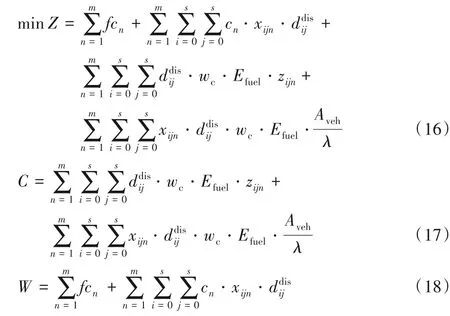
式(16)为模型三的目标数学模型,以运输成本和碳排放成本构成的总成本最小为目标函数;式(17)和式(18)分别表示该模式下相应的碳排放量和运输成本。以上三种模型有相同的约束,如下:
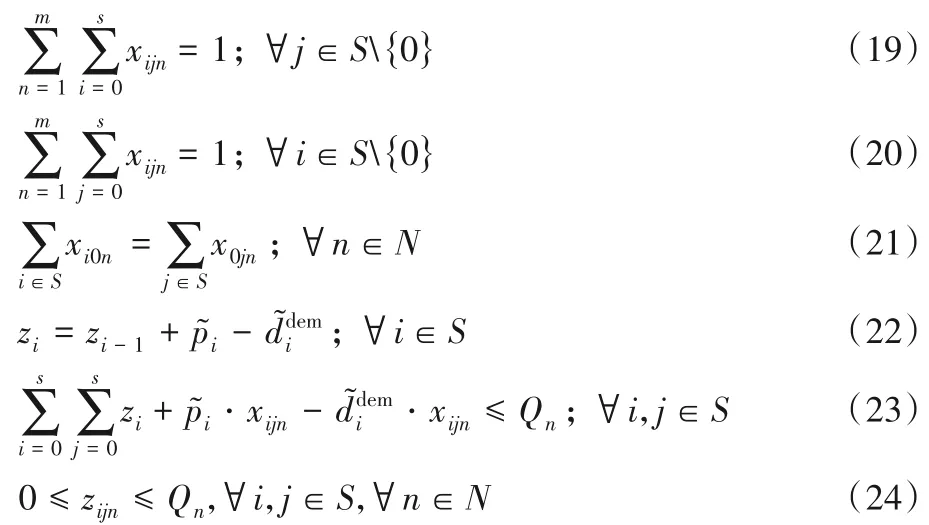
决策变量:

式(19)和式(20)表示每个客户仅由一辆车服务;式(21)表示运输车辆从配送中心出发,完成配送后最终回到配送中心;式(22)表示车辆离开客户i点时的载重量;式(23)表示车辆离开客户j点时的载重量不超过车辆的最大载重量;式(24)表示每辆车任何路段上的负载不得超过车辆最大负载限制,且非负;式(25)为决策变量。
2 差分进化算法及其改进方法
差分进化(Differential Evolution,DE)算法于1995 年由Storn 等[15]提出,是一种模拟自然界生物进化的智能算法,有较强的记忆能力,可动态调整搜索战略;同时,还具有较好的全局收敛能力和鲁棒性。在解决复杂全局优化问题时,过程更加简单,受控参数少,被视为仿生智能计算产生以来,在算法结构方面取得的重大进展[16]。基于此,本文采用差分算法求解低碳取送货车辆调度模型(Low Carbon Vehicle Routing Problem with Pickup and Delivery,LCVRPPD)。
2.1 个体编码解码
本文采用自然数编码方式,顾客集由{1,2,…,n}组成,0代表配送中心。假设现有12 个顾客需要被服务,用自然数1~12 表示这12 个顾客。首次,生成的一个个体如[3,6,8,7,12,10,11,9,5,2,4,1],然后根据各点的取送量和车载量进行编码,同时将配送中心0 插入到随机生成的个体后,形成一个完整的个体,如[0,3,6,8,7,0,12,10,11,0,9,5,2,0,4,1]。由此可得四辆车的配送路径如下:
车辆1:0—3—6—8—7—0
车辆2:0—12—10—11—0
车辆3:0—9—5—2—0
车辆4:0—4—1—0
2.2 适应度函数
本文研究目标函数设置更优问题。共建立三个模型,模型一以运输成本最小化为目标函数,同时记录碳排放量;模型二以碳排放量最小化为目标函数,并记录其运输成本;模型三中,将与油耗相关的碳排放成本作为成本一部分,构建总成本最小化为目标函数,并记录运输成本和碳排放量。
步骤1 以运输成本最小化为目标函数,运行算法50次,得到50 个解,并记录这50 个解对应的碳排放量C=
适应度函数如下:
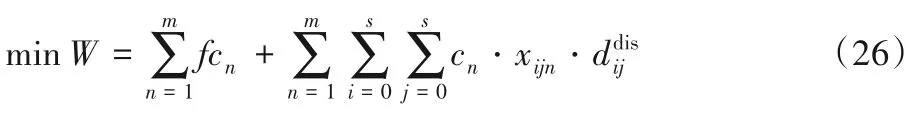
步骤2 以碳排放量最小为目标函数,运行算法50次,得到50 个解,并记录这50 个解对应的运输成本碳排放适应度函数如下:

步骤3 以运输成本和碳排放成本构成的总成本最小为目标函数,运行算法50次,得到50个解,并记录对应的运输成本和碳排放量C=适应度函数如下:
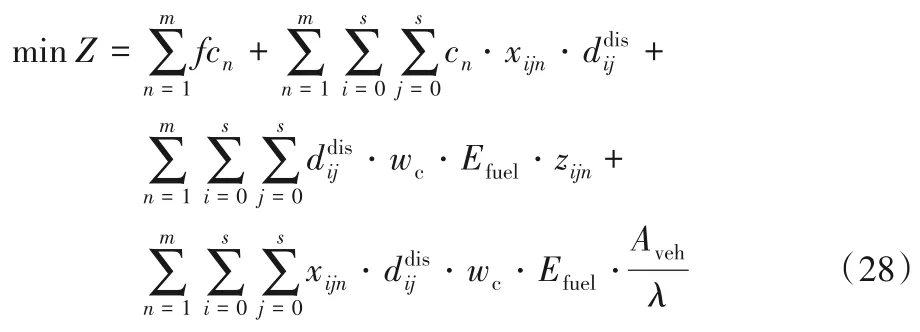
2.3 基于DE的更新操作
基于2-OPT 的变异算子。虽然差分演化算法具有结构简单、使用简单和鲁棒性好等特点,但同时也存在一定的缺点,在求解全局最优解时收敛慢,并且容陷入局部最优解。基于此,提出基于2-OPT 的差分算法。2-OPT 是局部搜索算法中的一种,工作原理是先求得一个解,将所得解的两条边进行交换然后求解得到一个新解。将新解和原解比较,择优淘劣。通过引入2-OPT算法,用新的变异方法取代DE 自身的变异机制,提高DE 的收敛速度。基于2-OPT 的差分算法变异操作[17-18]如下:

本文F设置为0.5[19-21]。简单举例:现对8 个顾客点,3 辆车,随机选出的3 个个体进行变异操作。其中3 个个体分别为:X1(1,3,5,0,8,2,0,4,0,6,7)、X2(3,0,5,7,0,4,1,0,2,8,6)、X3(8,5,0,3,2,1,0,6,0,7,4),具体变异过程如图1所示。
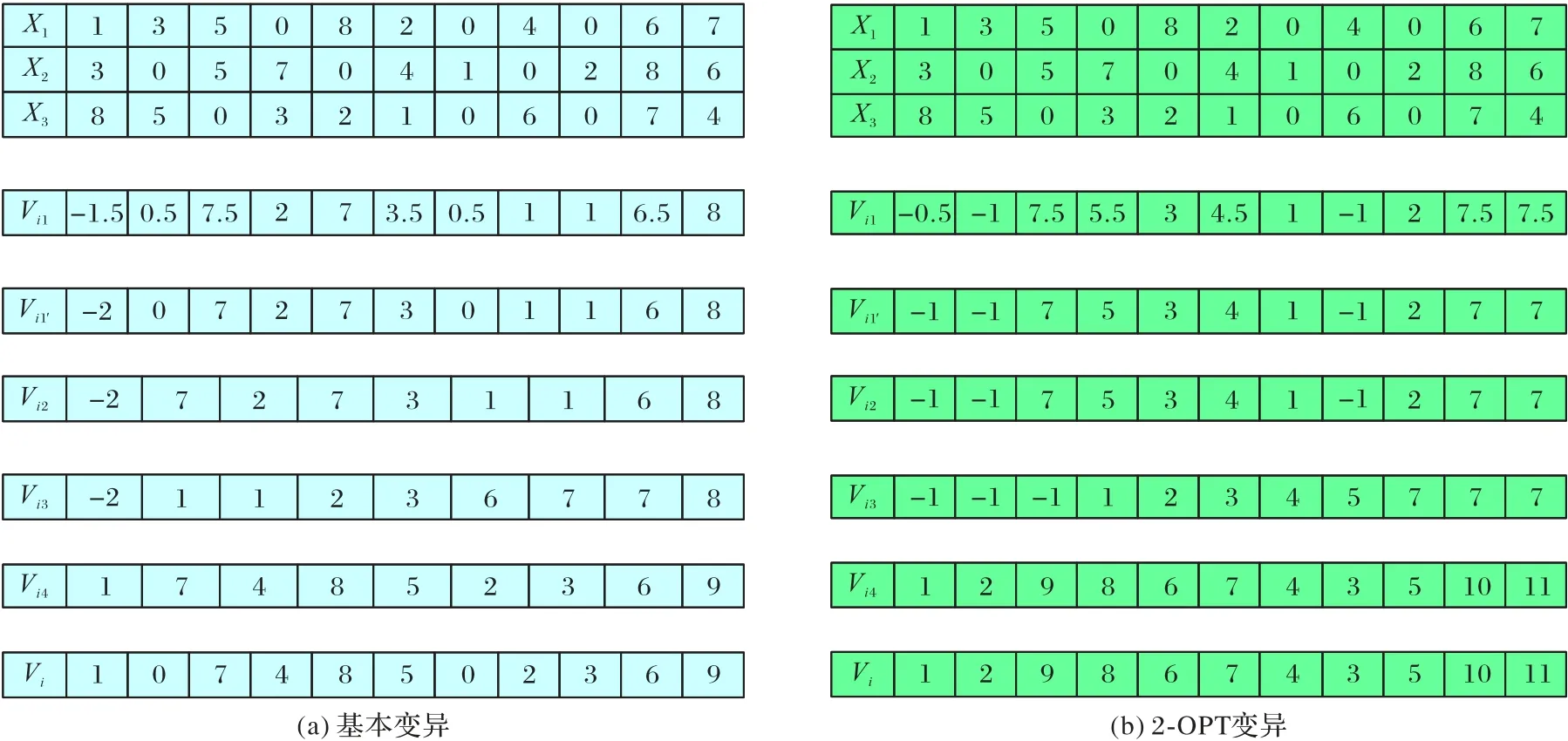
图1 变异操作Fig.1 Mutation operation
处理过程具体如下(两种方法仅计算公式不同,其他步骤均相同):
1)对8 个顾客点、3 辆车以及随机选出的3 个个体X1(1,3,5,0,8,2,0,4,0,6,7)、X2(3,0,5,7,0,4,1,0,2,8,6)、X3(8,5,0,3,2,1,0,6,0,7,4)进行变异及处理。
基本变异公式为:
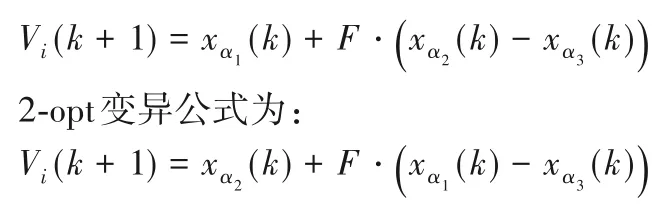
2)通过基本公式求得Vi1(-1.5,0.5,7.5,2,7,3.5,0.5,1,1,6.5,8),对其取整得到Vi1'(-2,0,7,2,7,3,0,1,1,6,8)。
3)提取Vi1'中0 并记录其所处的位置(0 的位置为2 和7)。当0 的个数超过车辆数时,只提取车辆数个0,得到Vi2(-2,7,2,7,3,1,1,6,8)。
4)将Vi2按照从小到大的顺序排列,得到Vi3(-2,1,1,2,3,6,7,7,8)。
5)用序号代替原编码值。例如Vi2中的-2 在Vi3中为第1位,则在Vi4中相应的位置填1;Vi2中的2 在Vi3中为第4 位,则在Vi4中相应的位置填4;依次得到Vi4(1,7,4,8,5,2,3,6,9)。
6)将步骤1)取出的0插入到原来的位置,得到Vi(1,0,7,4,8,5,0,2,3,6,9)。
二项交叉算子。交叉一般分为指数交叉和二项式交叉。父代和子代种群间交叉使用二项交叉更为有效,可充分利用各代种群间的信息,从而加速算法进行。基于此,本文采用二项交叉,具体见图2。
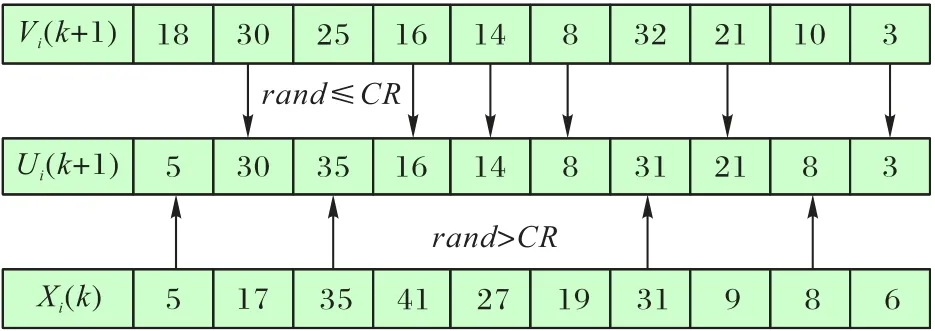
图2 交叉操作Fig.2 Crossover operation
贪婪选择算子。如果实验体的适应度值比目标个体的适应值更优异,则在下一代过程中实验体将取代目标个体,作为新的目标个体;否则,保持原有的目标个体。

该算法的总体流程如图3所示。

图3 总体流程Fig.3 Overall flowchart
3 案例研究
在案例研究部分,首先采用田口法确定相关参数最适合取值,在最佳取值情况下,对三种不同目标模型的运输成本和碳排放量进行比较,并对其进行相关性分析。最后将基本遗传算法(Genetic Algorithm,GA)、基本粒子群优化(Particle Swarm Optimization,PSO)算法和提出的基于2-OPT 的差分进化(Differential Evolution based on 2-OPT,DE-2OPT)算法对比,验证算法的有效性和合理性。所有启发式方法在计算机上使用Matlab R2012a 执行的,其带有AMD E1-1500 APU with Radeon(tm)HD Graphics 处理器,Windows 7旗舰版32位操作系统。案例中,Matlab 随机生成28个顾客服务点,考虑用6辆车辆配送,每辆车的载重量为10 t,每辆车的固定成本为300元,变动成本2 元/km,每升柴油5.8 元,整车质量为6.2 t,碳排放价格0.6 元/kg。假设配送中心位置为原点,28 个客户的坐标位置及模糊需求如表3所示。

表3 顾客相关信息Tab.3 Customer information
3.1 算法参数田口分析
田口分析法首次将产品设计思想和稳健性相结合,将噪声参数对系统的影响引入实验中,并通过实验找出最佳水平的组合。田口分析的函数共分为3 类,分别是望目特性的质量函数、望小特性的质量函数及望大特性的质量函数。本文目标函数是运输成本最小化和碳排放最小化,所以选择望小特性的质量函数。
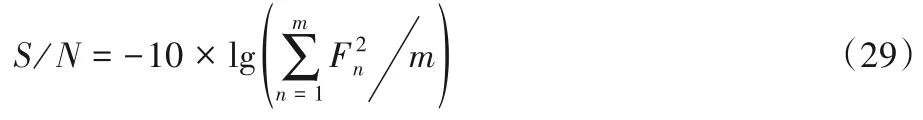
其中:m是不同参数组合运行的次数;F是响应函数值,即目标函数值;Fn是第n次的实验目标函数值。
算法效果对算法参数设置很敏感,不同参数设置影响算法的有效性。为探讨种群大小和迭代次数对算法的影响,将交叉常数CR(Cross)设置为0.9,缩放因子F设置为0.5,种群大小NP(Number of Population)分别设定为10、20、30、40、50,迭代次数分别为100、200、300、400、500,一共组成25个组合。选择的是L25(5*2)的水平用MINITAB 软件进行田口分析,分析结果见表4。
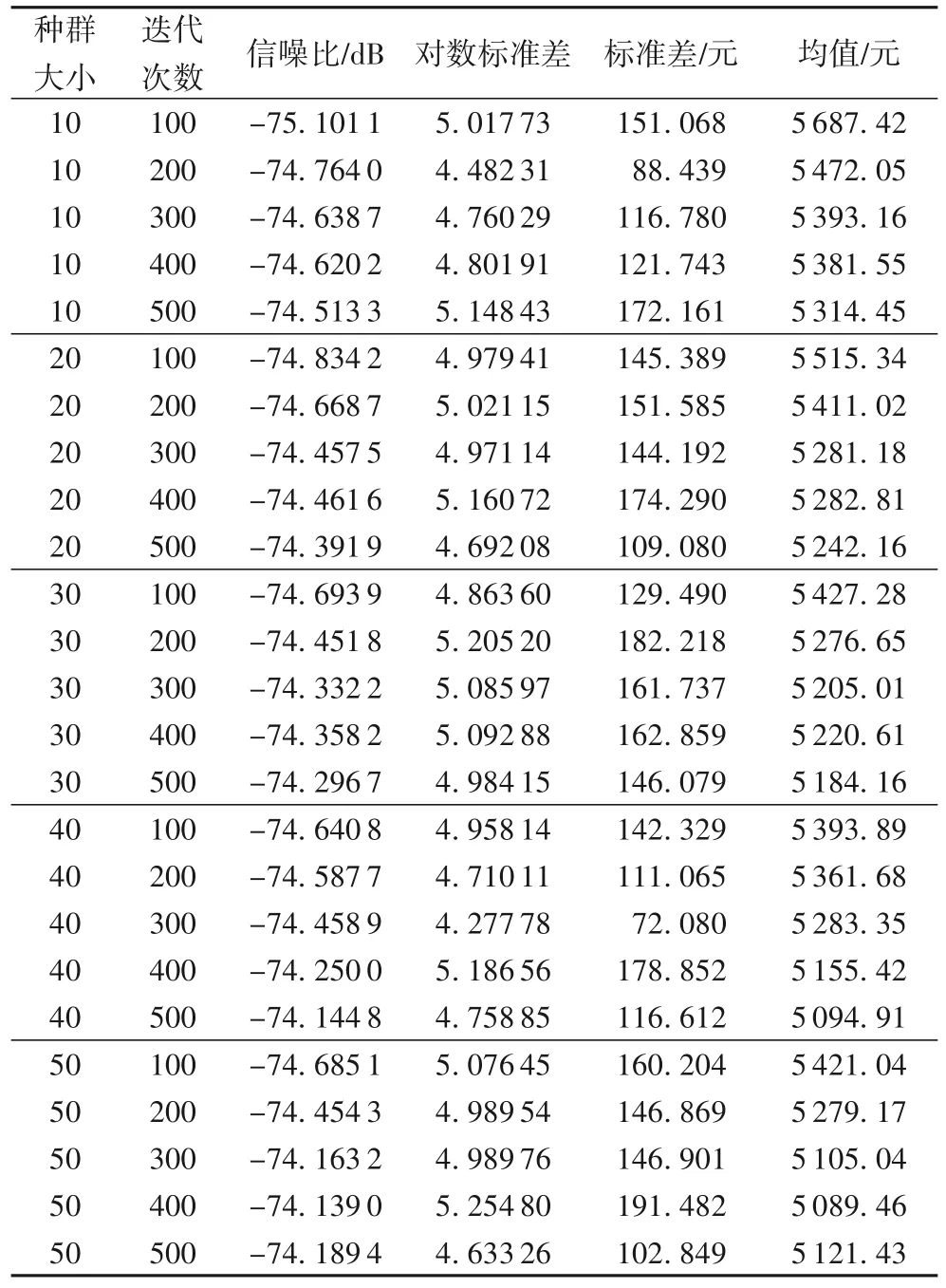
表4 田口分析Tab.4 Taguchi analysis
图4中,当种群大小NP=50,迭代次数为400时,信噪比最大(田口方法任何时候都是信噪比越大越好。图4 左下角的横坐标为种群大小,纵坐标为信噪比,当种群大小NP=50 时,信噪比数值最大;右上角的横坐标为迭代次数,纵坐标为信噪比,当迭代次数为400 时,信噪比数值最大。综上,当NP=50,迭代次数为400时,信噪比最大)。图5表示当种群为NP=50,迭代次数为400 时,均值最小(目标函数为最小化,均值则取最小值。图5 左下角的横坐标为种群大小,纵坐标为成本(单位:元),当NP=50时,成本最小;右上角的横坐标为迭代次数,纵坐标为成本(单位:元),当迭代次数为400 时,成本最小。综上,当种群为50,迭代次数为400 时,均值最小)。因此,根据田口分析法,设置种群大小为50,迭代次数为400。
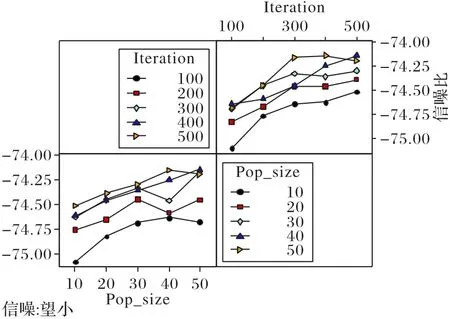
图4 信噪比交互作用图Fig.4 Signal-to-noise ratio interaction diagram
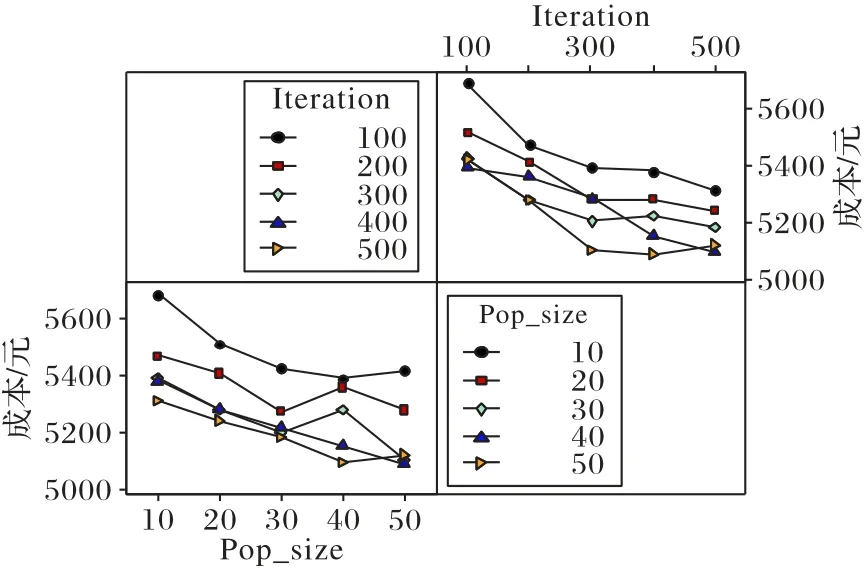
图5 成本均值交互作用图Fig.5 Cost mean interaction diagram
3.2 模型对比分析
根据田口法分析结果,种群大小设置为50,迭代次数为400。首先按2.2 节中适应度函数将三个不同目标模型分别运行50 次,记录50 个解对应的碳排放量和运输成本,散点图如图6所示。图6表明,三种模型下的运输成本和碳排放量均趋于正相关。因此,本文采用一款统计分析软件SPSS(Statistical Product and Service Solutions)对数据进行相关性分析,具体分析结果如表5和表6所示。
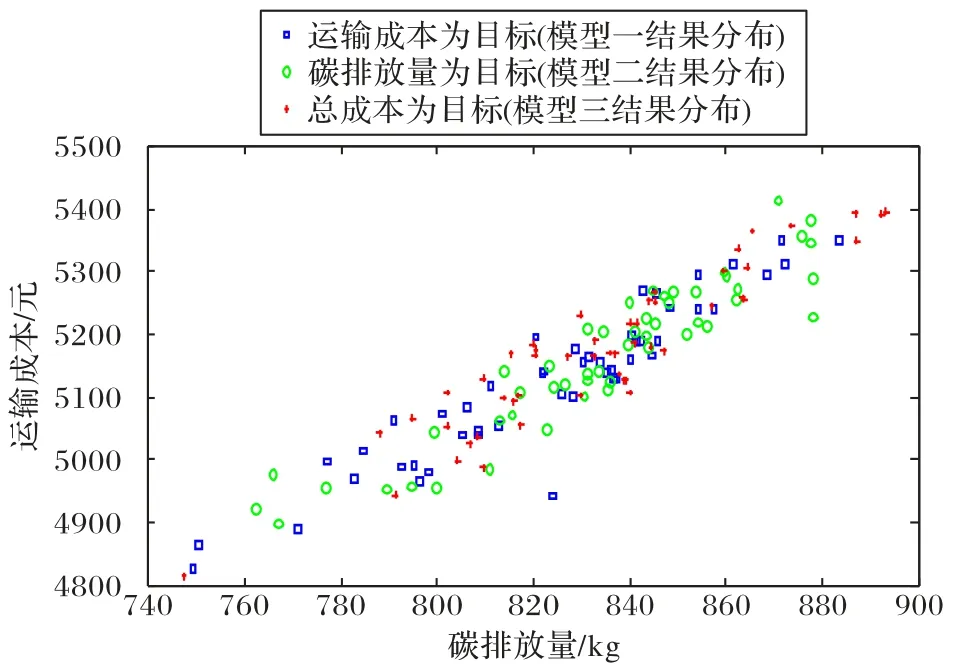
图6 不同目标下碳排放量和运输成本分布Fig.6 Distribution of carbon emission and transport cost under different objectives
由表5 的模型一可得,当运输成本最小为目标函数时,运输成本和碳排放量的相关性系数为0.928;由表5的模型二可得,当碳排放量最小为目标函数时,运输成本和碳排放量的相关性系数为0.932;由表5 的模型三可得,当总成本为目标函数时,运输成本和碳排放量的相关性系数为0.859。
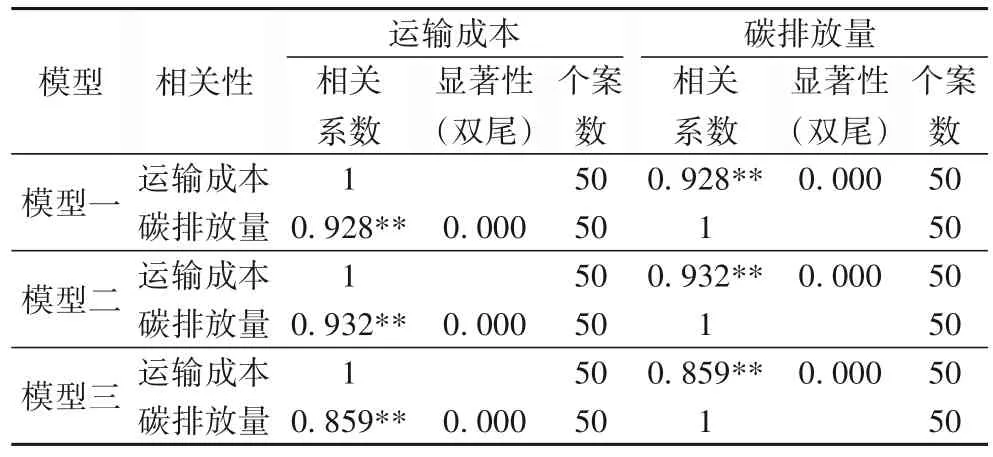
表5 三种模型下运输成本与碳排放量相关性分析Tab.5 Correlation analysis between transportation cost and carbon emission under three models
表6 是三种模型下150 组运输成本和碳排放量的相关性分析,相关性系数为0.920。以上相关性系数均在0.01级别,相关性显著。表6 表明运输成本和碳排放量相关性很高,为进一步探讨将目标函数设置合理性问题,将三种模型所对应的运输成本和碳排放量进行对比分析,见表7。

表6 总体的运输成本和碳排放量相关性分析Tab.6 Overall correlation analysis of transportation cost and carbon emission
运输成本最小为目标函数时,平均运输成本为5 127.66元,平均碳排放量为824.38 kg;碳排放量最小为目标函数时,平均运输成本为5 165.42 元,平均碳排放量为833.70 kg;总成本为目标函数时,平均运输成本为5 126.47元,平均碳排放量为822.42 kg。三个不同目标函数的运输成本方差分别为15 896.65 元2、15 634.52 元2和8 939.99 元2,碳排放量方差分别为915.07 kg2、864.33 kg2和479.85 kg2。综上,碳排放量与运输成本呈正相关关系,而以构建总成本最小的LCVRPPD模型,其对应解的效果更好。

表7 三种目标模型解的对比Tab.7 Comparison of solutions of three models with different objective functions
3.3 算法对比分析
为进一步验证该算法的有效性和合理性,本文将针对3种不同客户规模分别采用差分进化算法(DE)、基本遗传算法(GA)、基本粒子群优化(PSO)算法和提出的基于2-OPT 的差分算法(DE-2OPT)进行求解,并对比其计算结果。相应参数如表8所示,其中:NP为种群大小,G为迭代次数,W为学习因子,R为变异概率,C为交叉概率,CR为交叉常数,F为缩放因子。

表8 各算法对应参数Tab.8 Corresponding parameters of different algorithms
将客户分为25、50 和75 个三种规模,并将各算法分别运行20次,分别取各算法最优解。计算结果如表9所示,算法迭代效果图如图7所示。由表9可以得出,本文提出的算法求解结果优于差分进化算法、传统遗传算法和粒子群优化算法。当客户数量为25 时,与差分进化算法相比,本文提出算法的总成本降低1.8%,碳排放量降低0.7%;与遗传算法相比,本文提出算法的总成本降低1.9%,碳排放量降低1.2%;与粒子群优化算法相比,本文提出算法的总成本降低4.0%,碳排放量降低1.56%。
当客户数量为50 时,从表9 可看出,与差分进化算法相比,本文提出算法的总成本降低1.75%,碳排放量降低2.9%;与遗传算法相比,本文提出算法的总成本降低4.2%,碳排放量降低6.5%;与粒子群优化算法相比,本文提出算法的总成本降低4.8%,碳排放量降低14.35%。
当客户数量为75 时,从表9 可得出,与差分进化算法相比,本文提出算法的总成本降低3.0%,碳排放量降低3.5%;与遗传算法相比,本文提出算法的总成本降低16.47%,碳排放量降低4.3%;与粒子群优化算法相比,本文提出算法的总成本降低22.5%,碳排放量降低7.88%。
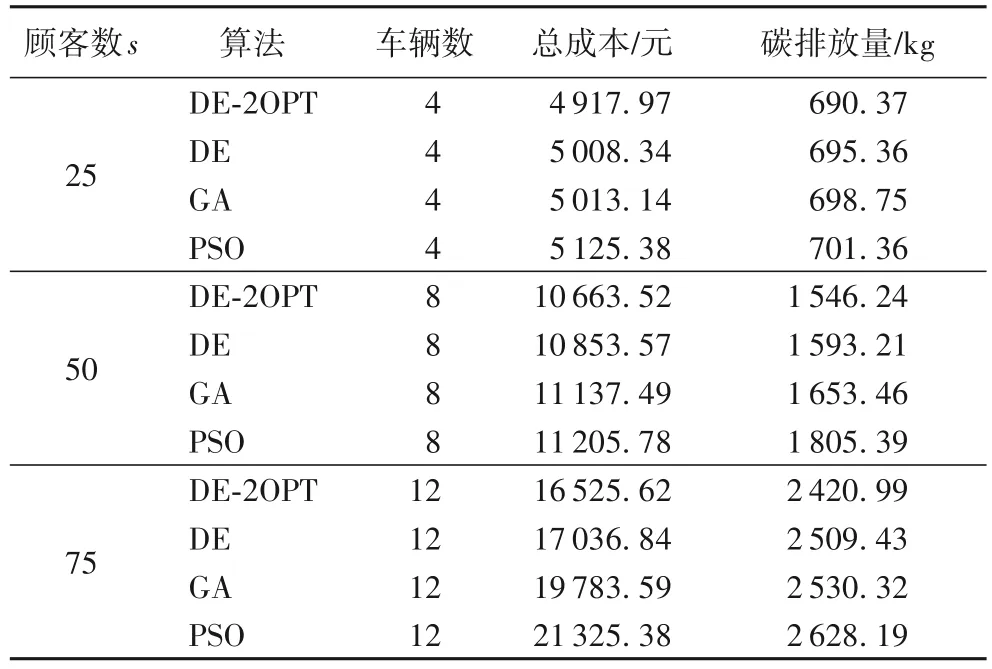
表9 不同规模客户四种算法结果对比Tab.9 Comparison of results of four algorithms for customers with different scales
由图7 可以得到,随迭代次数的增加,解趋向于稳定并且越来越优。其中可以看出:GA计算时间长、收敛慢,但是其求解效果好,全局寻优能力强;PSO 算法易陷入局部最优解,挖掘能力较差,求解时间短;DE算法收敛快,但较易受种群个体大小的影响;DE-2OPT算法有较好的全局收敛能力和鲁棒性,收敛较快。故而,认为DE-2OPT 对于求解所提出的模型是有效的。

图7 算法迭代对比Fig.7 Algorithm iteration comparison
4 结语
本文基于模糊需求下同时取送货问题,研究探讨低碳目标函数设置问题,分为三种情况:一是以运输成本最小、二是以碳排放量最小、三是由运输费用和碳排放费用构成的总成本最低。随后,提出基于2-OPT 的差分进化算法求解模型。案例研究中,首先采用田口法获取相关参数的合理取值。随后通过SPSS 分析得出:当运输成本最小为目标函数时,运输成本和碳排放量的相关性系数为0.928;当碳排放量最小为目标函数时,运输成本和碳排放量的相关性系数为0.932;当总成本最小为目标函数时,运输成本和碳排放量的相关性系数为0.859。同时分析三个目标函数下150 组运输成本和碳排放量的相关性,其相关性系数为0.920。
因运输成本和碳排放量相关性显著,为进一步探讨将目标函数设置合理性问题,将三种模型所对应的运输成本和碳排放量进行对比分析。运输成本最小为目标函数时,平均运输成本为5 127.66 元,平均碳排放量为824.38 kg;碳排放量最小为目标函数时,平均运输成本为5 165.42元,平均碳排放量为833.70 kg;总成本为目标函数时,平均运输成本为5 126.47 元,平均碳排放量为822.42 kg。3 个不同目标函数的运输成本方差分别为15 896.65、15 634.52 和8 939.99,碳排放量方差分别为915.07、864.33 和479.85,总成本最小为目标函数时稳定性最好。
综上,碳排放量与运输成本呈正相关关系,同时构建总成本最小的LCVRPPD 模型,其对应解的效果更好。最后对DE-2OPT、DE、GA 和PSO 四种算法进行对比,验证该算法的有效性及合理性。本研究仍存在一些不足,例如没有考虑天气、不同车型以及顾客的满意度对运输过程的影响,这些将是进一步研究的方向。
