多因素耦合影响下隧道电子雷管爆破参数的计算与实践
2021-03-17刘翔宇吴昊骏
刘翔宇,龚 敏,吴昊骏,安 迪
(北京科技大学 土木与资源工程学院,北京 100083)
电子雷管起爆作为一种新型爆破技术,是精准控制爆破的发展方向,其最大特点为起爆延时精度高[1],城市隧道爆破采用电子雷管起爆已取得良好的爆破与降振效果[2-3]。 但目前并没有一套公认成熟的电子雷管爆破设计方法,其精度优势尚未在工程中得以充分发挥,如何研究与电子雷管相匹配的爆破参数计算方法,是目前亟待解决的问题。
隧道爆破设计的关键是确定起爆药量和延时时差,其余参数大都可据此推出。对于起爆药量,目前仍是依据萨氏公式进行计算,但结果往往有较大偏差;孔间延时设计总体上分为两类:一类根据工程经验结合现场试验确定[4-6],该方法需根据具体工程进行多次调整,相对繁琐,不具有普遍适用性;另一类是目前较为认可的主流方法,即基于波形理论提出的半周期错相减振计算法[7-9],将振动波形简化为带阻尼的余弦波,但实际爆破振动波形并不是严格的周期波,且地下岩体的复杂多变性导致爆破振动波是随机的,其适用性有待进一步验证。此外更重要的是,以上方法均是针对单一参数特性的研究,隧道毫秒爆破的参数之间相互影响,微差时间、单孔药量、爆破孔数与振速叠加存在复杂的耦合关系,而考虑多参数相互作用影响的设计方法尚无人研究。吴昊骏等[10-11]曾基于多孔微差振动合成方法,考虑非电雷管的实际延时范围对非电雷管的爆破参数进行了精确计算。但由于非电雷管的延时误差大,难以进一步研究多参数之间的耦合关系。
为解决以上问题,本文在电子雷管精确起爆特性的基础上,考虑多孔微差振动合成,提出基于多参数耦合下的爆破参数计算方法,以现场获取的单孔振动曲线为依据,充分考虑实际爆破振动衰减特性,在不同药量、不同孔数、不同微差时间多种参数组合作用下,利用振动波合成理论和计算程序求解振动合成曲线,选取最优干扰消振的爆破参数;通过比较电子雷管不同孔间延时的计算合成曲线与实测振动曲线差异,得到了较以前方法更准确可靠的爆破第二临空形成时间。从理论分析、实际应用上将目前使用的半周期错相减振法与本方法进行对比分析,指出前者的适用范围。
1 基于多参数耦合的电子雷管爆破参数计算法
Anderson等[12-13]提出了基于现场爆破单孔振动波形计算微差爆破振动合成的方法,国内外学者据此进行了大量研究。但众所周知,普通雷管延期误差大,每段实际都是一个变化的延时时段,这给计算多孔微差振动合成带来很大困难,而且与实际情况出入较大。为解决上述问题,吴昊骏等在爆前实测样本雷管延时范围,根据单孔振动数据计算微差延时范围内所有可能的合成振动组合,以最不利情况设计药量,但因段位延时是固定的,实际上不能设计延时时间,且计算药量时只能取所有可能延时中的药量最低值以确保安全,仍不能实现精准高效爆破。
现场实践表明,爆破振动波形十分复杂,并不是严格的周期波。图1是典型单孔爆破振动波形图,从图1可知,每个周期时间均不相同,每一周期的峰值点与其对应时间都有很大差异,如按此曲线进行微差振动合成,微差时间影响药量的选取,参与微差爆破孔数影响微差时间的选取,药量、微差时间、爆破孔数等多个参数之间的复杂关系都将对振动合成产生影响,极大增加了爆破设计难度。而这是以前研究未曾考虑的因素。

图1 典型单孔爆破振动波形的过零点时刻图
1.1 基本思路
电子雷管1 ms的延时精度为用计算机精确计算多孔爆破振动合成提供了可能,这是实现本文研究的基础。
针对以上情况,本文计算爆破参数总体思路是,鉴于电子雷管隧道爆破通常为逐段逐孔起爆方式,采用安德森法原理,利用现场爆破振动实测数据结合计算程序,充分考虑爆破振动波形的复杂性及衰减特性,通过分析多参数不同组合下的振动叠加波形,考虑不同孔间延时、不同孔数振动合成、不同药量与控制振速之间多参数耦合的定量化关系和第二临空面形成时间,综合后得到优化的爆破参数。
具体而言即为:
现场进行单孔单自由面不同药量爆破,获得被保护物位置处爆破振动曲线;
在同一药量下逐一计算不同孔间延时(1~10 ms)下、不同孔数微差起爆合成振动曲线;首先重点分析爆破孔数对孔间延时的影响,再根据上述结果分析不同孔数振动合成的最大合成振速变化,确定爆破孔数;
以上述程序对不同药量进行计算分析,选取安全控制振动峰值下最大掏槽单孔药量和对应孔间延时时间;
现场试验结合理论计算确定第二临空面形成时间,即可确定其它爆破参数,在隧道爆破中实现安全振速下的进尺最大化。
以上是在综合考虑爆破多参数之间复杂的耦合关系后,得到基于多孔微差爆破振动合成计算的电子雷管爆破设计方法,为方便起见以下简称“多因素耦合法”。
1.2 本文计算爆破参数方法的实施步骤
隧道爆破的振动控制,主要是降低掏槽爆破的振动强度[14],因此本文首先确定掏槽孔爆破参数,再确定其余炮孔参数。
如前所述,除微差时间外,药量和爆破孔数都将对振动叠加产生影响。基于现场实测的不同药量单孔振动波形,以电子雷管的起爆精度为计算延时间隔,本文提出的电子雷管爆破参数设计的多因素耦合法具体实施步骤如下:
步骤1 现场试验。
在隧道现场实测不同药量的单孔单自由面振动波形(与掏槽爆破条件保持一致),测试3次以上,选取其中典型波形作为后面进行计算的波形。
步骤2 实测单孔振动曲线的拟合。
为利用计算机进行振动合成计算的需要,将单孔波形拟合为函数形式。为此采用MATLAB软件,利用Fourier级数拟合单孔波形,函数形式如下:
(1)
式中:f(t)为单孔波形拟合函数;t为时间;a0、ai、bi为Fourier拟合系数;ω为基频;k为Fourier拟合级数。曲线拟合精度由拟合级数k控制,k的取值,根据波形拟合精度进行调整。各参数的计算公式如下
ω=2π/T
式中:T为波形截断时间;M为总采样点数;ym为第m个采样值。
根据单孔波形截断时间,将拟合函数扩展至时间全域波形函数v(t),如下:

(2)
式中:v(t)为时间全域波形拟合函数;t为时间;T为波形截断时间。
步骤3 不同孔间延时与不同爆破孔数组合下的振动合成计算。
利用MATLAB软件,选择微差时间和掏槽孔数的一个组合(Δt,N)对垂直振速v(t)(垂直振速对临近地面建筑物安全影响最大)进行线性叠加计算,不断改变(Δt,N)反复计算,得到(Δt,N)所有组合的计算合成振动曲线及对应的最大合成振速。
各掏槽孔的药量相同,通常情况下隧道爆破炮孔间距远小于隧道与地面的距离(当隧道距地面建筑20 m时,4 m孔口距的各掏槽孔至地面建筑空间距离误差不大于6.7%,振速误差仅为0.3%),可将多个炮孔视为同一爆源,认为N个掏槽孔的振动波形相同。振动叠加计算公式如下
Δtn=(n-1)Δt
(3)
式中:V(t,{Δtn})为合成波形函数;v(t)为时间全域波形拟合函数;Δtn为第n个掏槽孔的起爆时间;Δt为相邻孔间延时。
V(t,{Δtn})的最大合成振速Vmax(t,{0,Δt,2Δt,…})为正、负向最大振速绝对值的较大值。
步骤4 基于多因素耦合的最优药量、孔间延时与掏槽孔数的选取。
(1) 确定药量和掏槽孔数的取值范围。所有药量取值构成集合A{Q1,Q2,…};所有掏槽孔数取值构成集合B{N1,N2,…}。
(2) 在集合A、B中,选择药量和掏槽孔数的一种组合,按照不同Δt进行多孔振动叠加计算,得到V(t,{Δtn})。取所有Vmax(t,{0,Δt,2Δt,…})的最小值Vmin,其对应的Δt定义为最优微差时间。
Vmin={Vmax(t,{0,Δt,2Δt,…})}min
(4)
最优微差时间是本文为方便爆破设计特别定义的一个参数,是指计算得到不同孔间延时合成振速曲线后,将这些曲线的最大合成振速值进行比较,其中最小值对应的孔间延时称为最优微差时间。
(3) 采用枚举法,遍历药量和掏槽孔数的所有组合,重复第二步计算过程,得到所有药量和掏槽孔数组合下的最优微差时间及对应的Vmin。
将所有组合的Vmin与安全振速进行对比,并结合现场隧道断面大小,确定单孔药量、掏槽孔数和最优微差时间等爆破参数。
1.3 第二临空面形成时间的精确确定及相关参数设计
第二临空面的形成对爆破降振与爆破效果具有重要意义。初始起爆的掏槽爆破只有一个临空面,若能准确确定掏槽爆破中第二临空面的形成时间,就可根据具体情况调整掏槽孔临空面形成前后的爆破参数,充分利用第二临空面的降振作用和破岩作用,达到精准控制爆破目的。
龚敏等此前通过对比8孔逐孔微差起爆计算合成振动波形与现场实测振动波形的差异,确定了普通雷管起爆下第二临空面的形成时间范围。但这一方法是有缺陷的。国内普通雷管即使采用逐孔逐段起爆,每段之间延时间隔也通常达数十毫秒之多,因此若第二临空面在两段间形成,其误差也可达数十毫秒而不能更进一步确定。但电子雷管由于孔间延时能精确设计到1 ms,因此能很方便地设计短延时微差起爆网络,相比非电雷管可以更精确地确定第二临空面形成时间。
基于电子雷管第二临空面的精确确定方法如下:首先设计电子雷管短延时(10 ms内)逐孔微差掏槽爆破,然后根据本文式(3),得到计算合成振动曲线;在现场实测相应爆破振动曲线,将计算合成振动曲线与实测振动曲线放在同一张图中比较,定义相同时刻的振速差异达到50%以上即为第二临空面形成时间。
第二临空面形成后爆破参数设计方法如下:临空面形成后由于爆破条件改善,炮孔药量较形成前减少20%~30%,普通雷管起爆时为节约段数可采用两孔或多孔同段;电子雷管由于不受段别数量限制仍可采用逐孔逐孔爆破。
2 多因素耦合法计算爆破参数实例
2.1 工程背景
重庆市观音桥北大道隧道位于重庆市中心区,施工区间有密集的地面建筑物及地下管线,隧道埋深20~30 m,属浅埋隧道。爆破区岩性主要为灰色、灰白色砂岩,无不良地质现象,隧道围岩类别为IV级。爆破试验在隧道左洞K1+330~K1+367区段进行,隧道断面尺寸为11.8 m×9.55 m,断面面积90.85 m2。为确保隧道的施工安全及周围建构筑物的结构安全,要求地面振速不超过1.0 cm/s。
下面将根据多因素耦合法设计掏槽孔爆破参数孔间延时及单孔最大药量。
2.2 不同药量单孔单自由面爆破试验及振动波形拟合
在隧道现场,实测1.0 kg、1.2 kg、1.4 kg三种药量的单孔单自由面爆破振动波形,单孔爆破现场试验示意图如图2(a)所示,测点布置在隧道工作面的地面正上方(地面距爆源最近处),其中炮孔直径φ42 mm、炮孔深度2.5 m、采用2号岩石乳化炸药(药卷直径φ32 mm)。各药量的典型单孔波形如图2(b)所示,单孔最大振速依次为0.366 cm/s、0.512 cm/s、0.897 cm/s。
如图3所示,110 ms之后的振速已几乎衰减为0,但为确保各个波形充分叠加,在140 ms处将单孔波形截断。
利用MATLAB软件编程计算截断波形的拟合函数f(t)。以1.4 kg药量为例,当k取值32时,曲线拟合的相关系数为0.997,标准差为0.005 4,确定k值为32,得到截断波形的拟合函数f(t)。如图3所示,拟合曲线与实测波形曲线几乎完全重合。将截断波形函数f(t)扩展至时间全域,得到用于多孔微差振动叠加计算的单孔波形函数v(t)。
2.3 爆破参数多因素耦合关系的研究
如前所述,药量和爆破孔数都将影响微差时间的选取。因此,在设计爆破参数前,首先需要计算研究药量、掏槽孔数、微差时间和最大合成振速等多参数的耦合关系,然后据此确定药量、孔间延时、掏槽孔数等爆破参数。

(a) 单孔爆破现场试验示意图

(b) 现场实测单孔单自由面振动波形图2 单孔单自由面爆破现场试验Fig.2 Blasting field test of single hole with single free surface

图3 单孔波形的拟合曲线与实测曲线对比
具体方法如下:当药量和掏槽孔数为某一组合确定值时,计算不同孔间延时的合成振动曲线,确定最优微差时间(方法见1.2节),分别改变药量和掏槽孔数重复计算,得到药量和掏槽孔数不同组合的最优微差时间及最优微差时间对应的最大合成振速,研究药量、掏槽孔数变化对最优微差时间及最大合成振速的影响。
根据现场施工经验,电子雷管同类型炮孔(如掏槽孔)孔间延时Δt相同,且通常取值在10 ms以内;但具体取值主要依靠经验。在采用本文多因素耦合法后,可根据单孔拟合函数v(t)和式(3),以1 ms为增量,利用MATLAB软件编程分别计算1.0 kg、1.2 kg、1.4 kg三种药量下掏槽孔数和孔间延时不同组合的合成振速V(t,{Δtn})。考虑所有的实际可能情况,本文计算掏槽孔孔数取值2~20,孔间延时取值1~10 ms。
2.3.1 药量和掏槽孔数对最优微差时间的影响分析
三种药量下不同掏槽孔数的最优微差时间,如图4所示。

图4 各药量不同掏槽孔数的最优微差时间
由图4可知,不同药量的最优微差时间不同。掏槽孔数N对最优微差时间有显著影响,1.0 kg药量下,掏槽孔数为2~4时,最优微差时间随掏槽孔数而变化,掏槽孔数大于4时,最优微差时间为定值5 ms;1.2 kg、1.4 kg药量下,掏槽孔数为2~15孔时,最优微差时间随掏槽孔数而变化,掏槽孔数大于15时,两种药量最优微差时间不再变化,均为4 ms。
2.3.2 药量和掏槽孔数对最大合成振速的影响分析
三种药量下,不同掏槽孔数的最大合成振速(按照最优微差时间进行微差振动合成计算)如图5所示。

图5 三种药量下不同掏槽孔数的最大合成振速
由图5可知,不同掏槽孔数的最大合成振速有显著差异。1.0 kg药量下,掏槽孔数为2~12时,最优微差时间下的最大合成振速随掏槽孔数而变化,其值为0.357~0.449 cm/s,最大差值0.092 cm/s;掏槽孔数大于12时,最优微差时间下的最大合成振速为定值0.357 cm/s。1.2 kg、1.4 kg药量下,掏槽孔数为2~15时,最优微差时间下的最大合成振速随掏槽孔数而变化,1.2 kg药量最优微差时间下的最大合成振速为0.495~0.570 cm/s,最大差值0.075 cm/s,1.4 kg药量最优微差时间下的最大合成振速为0.892~1.022 cm/s,最大差值0.130 cm/s;掏槽孔数大于15时,两种药量最优微差时间下的最大合成振速不再变化,分别为0.495 cm/s、0.904 cm/s。
综上所述,在同一药量下,不同掏槽孔数、孔间延时、爆破振速3个参数间具有互相影响的复杂耦合关系,因此上述参数需综合考虑其影响后进行确定;另外需注意的是:当爆破孔数超过某一临界值后(本例为16孔),最优微差时间和对应最大合成振速均不再变化,设计施工时这一临界值的确定具有重要的工程意义。
2.4 掏槽孔微差爆破参数设计
首先确定掏槽单孔药量和掏槽孔数。根据2.3节的计算结果,1.0 kg、1.2 kg药量,各掏槽孔数的最大合成振速不大于0.449 cm/s、0.570 cm/s,均远小于安全振速1.0 cm/s;1.4 kg药量,各掏槽孔数的最大合成振速不大于1.022 cm/s,其中掏槽孔数为2、3、8、9、11及大于16时,最大合成振速为0.9 cm/s,小于安全振速。
根据开挖断面大小,掏槽孔数小于10个为宜,楔形掏槽孔数为偶数,掏槽孔数取2时太少。综上,现场设计8个(4对)掏槽孔,取1.4 kg作为掏槽孔的单孔设计药量。
根据1.4 kg药量,1~10 ms微差时间下的8孔最大合成振速,如图6所示,设计其相邻孔间延时。

图6 1.4 kg药量1~10 ms最大合成振速
1.4 kg药量在微差时间为4 ms、5 ms时,最大合成振速均较小。故设计孔间延时Δt为4~5 ms。
3 本文爆破参数计算方法的现场验证
3.1 不同孔间延时下合成振速变化的现场对比
为进一步验证本方法的应用效果,在隧道现场进行电子雷管不同微差时间的爆破振动强度对比试验。炮孔布置图及孔间延时设计如图7所示,分别针对:①区域掏槽孔;②区域辅助孔设计不同微差时间的对比试验。

图7 炮孔布置图及孔间延时设计图
3.1.1 掏槽区不同微差时间干扰降振试验比较
掏槽区的炮孔布置如图7①区域所示,设计8孔掏槽爆破不同孔间延时5 ms和8 ms的对比试验。5 ms孔间延时,8个掏槽孔单孔装药量均为1.4 kg;8 ms微差时间,首爆孔的单孔药量为1.2 kg(因孔深未达到设计深度),其他7孔单孔药量均为1.4 kg。
掏槽孔5 ms和8 ms孔间延时的微差爆破振动波形对比如图8所示。对比5 ms和8 ms微差的最大振速:微差时间为5 ms和8 ms时,最大振速分别为0.913 2 cm/s、1.035 cm/s,5 ms微差的最大振速与2.4节计算预测值非常相近,并比8 ms微差的最大振速小0.121 8 cm/s。

图8 掏槽区5 ms和8 ms微差爆破振动波形对比图
微差时间为5 ms时,最大振速对应时间为4.5 ms,在第2个掏槽孔起爆前,说明之后相继起爆的7个掏槽孔的爆破振动正向与负向异向相消,振速干扰相减。当采用5 ms孔间延时时,能最大程度的实现合成振动峰值互相削减,最大振速为单孔最大振速,很好的实现了干扰降振;微差时间为8 ms时,最大振速对应时间为25.625 ms,在第4个掏槽孔起爆后、第5个掏槽孔起爆前,说明前4个掏槽孔相继起爆后,各孔的爆破振动产生了同向叠加相增。
3.1.2 辅助孔不同微差时间干扰降振试验对比
同时,在辅助孔区域进行3 ms、5 ms、8 ms微差时间的对比试验,炮孔布置图、微差时间设计如图7②区域所示,1~4排炮孔的微差时间依次为8 ms、5 ms、3 ms和5 ms,单孔药量均为1.0 kg。其中1排与2排爆破条件及临空面条件相同,3排与4排爆破条件及临空面条件相同,对应振动波形如图9所示,竖向虚线为各排炮孔首爆孔起爆时间。
由图9可知,1排(孔间延时8 ms)的最大振速为0.518 cm/s,2排(孔间延时5 ms)的最大振速为0.37 cm/s,5 ms微差的最大振速比8 ms微差小0.148 cm/s。3排(孔间延时3 ms)的最大振速为0.645 cm/s,4排(孔间延时5ms)的最大振速为0.321 cm/s,5 ms微差的最大振速比3 ms微差小0.324 cm/s。
后续循环均采用5 ms作为掏槽孔的孔间延时,现场实测振速控制效果良好。

图9 辅助区不同微差时间振动波形图
3.2 确定第二临空面形成时间的现场试验
第二临空面形成后振速显著下降。对于最佳微差时间的选取,还需要考虑第二临空面的形成时间,定义第二临空面形成时间为振速下降50%时刻。
龚敏等[13]通过对比分析非电雷管的掏槽孔8孔振动合成计算波形与现场实测波形,得出第二临空面形成时间在50~70 ms时段内的结论,但由于普通雷管相邻段间延时过长,同段延时范围较大,无法进一步缩小时段,不利于振速的精准控制。
根据本文1.3节所述方法,可以更准确判断第二临空面形成时间。设计1.4 kg单孔药量、5 ms和8 ms两种孔间延时在观音桥隧道进行现场爆破,并分别测取隧道正上方两个不同孔间延时的爆破振动波形,再计算两次试验各自微差爆破合成振动曲线,以此更精确的确定第二临空间形成时间。


图10 5 ms微差时间的计算振速曲线与实测振动波形对比图
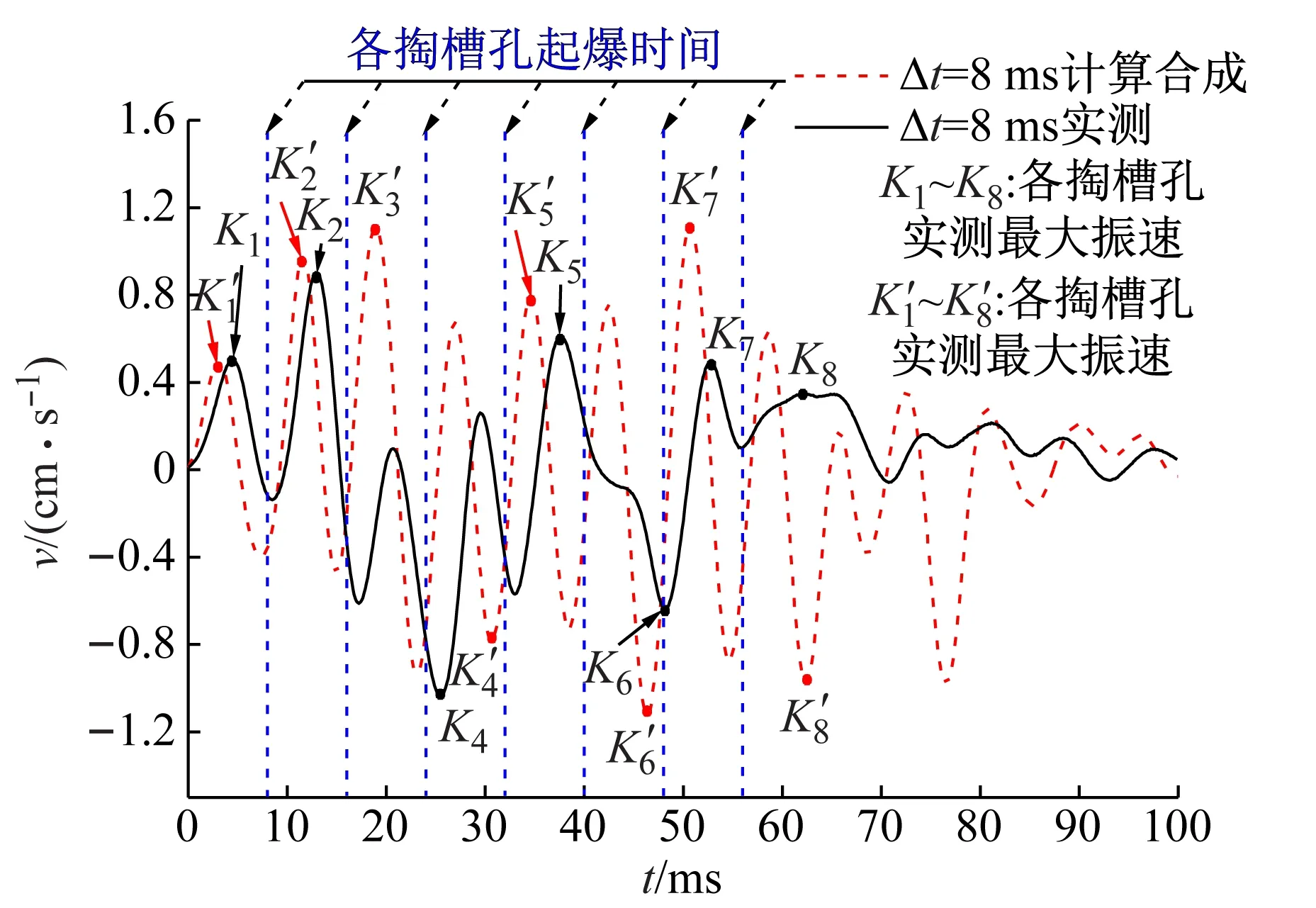
图11 8 ms微差时间的计算振速曲线与实测振动波形对比图
由于地下岩土性质的复杂多变性,计算合成曲线与实测振动曲线不可能完全一致。为进一步量化分析,绘制8个掏槽孔依次起爆后的计算合成最大振速与实测最大振速比值图,如图12所示。

图12 实测振速与计算振速比值Fig.12 Ratio of measured velocity to calculated one
从图12可得到,微差时间为5 ms时,前6个掏槽孔的计算合成最大振速和实测最大振速相近,掏槽孔⑦和掏槽孔⑧的实测振速分别为计算合成振速的82.7%、84.5%,振速有所下降但并不显著,判断掏槽孔⑧起爆时第二临空面未形成。微差时间为8 ms时,前4个掏槽孔起爆后的计算最大振速与实测最大振速相近,掏槽孔⑤至掏槽孔⑧起爆后的实测最大振速与计算最大振速的比值逐渐减小,依次为76.7%、56.6%、44.1%、35.9%,掏槽孔⑦起爆时(48 ms)实际振速小于合成振速的50%,判断此时已形成第二临空面,即起爆后48 ms已形成了第二临空面。
由图12可知,相邻掏槽孔间距为0.45 m,若相邻孔的微差时间足够长,使得先爆掏槽孔形成足够大的空洞,相邻后爆掏槽孔的振速将显著下降。当孔间延时取较小值时,掏槽孔在短时间内相继起爆,从岩石开始移动、裂纹扩展到形成空洞需要一定时间[15],在形成第二临空面(足够大的空洞)时,可能所有掏槽孔均已起爆。
综上,采用微差时间8 ms进行掏槽爆破时,掏槽孔⑦起爆时第二临空面已形成,但前4孔振动控制效果不佳;采用最优微差时间5 ms进行掏槽爆破时,虽然所有掏槽孔起爆时均未形成第二临空面,但通过最大程度的异向干扰降振实现了较好的振动控制效果。这表明,对于短微差延时掏槽爆破,即使未形成第二临空面,但通过多因素耦合法合理设计孔间延时,同样可以实现良好的降振效果。
4 多因素耦合法与半周期错相减振法对比
为了评估多因素耦合法的减振效果,以下将其与主流的半周期错相减振法进行对比,确定半周期错相减振的适用范围。
4.1 半周期错相减振法
半周期错相减振法将爆破振动波视为周期波,将波形半周期作为孔间延时,是目前设计电子雷管孔间延时的常用方法。半周期错相减振法将爆破产生的振动速度表示为带阻尼的余弦函数如式(5),以两个振动波形之间相差n/2个周期(n=1,3,5,…,n尽可能取小值)作为孔间延时。
(5)
式中:K和α为场地因数;Q为单段装药质量;r为测点到爆区的距离;ξ为阻尼;ω为振动圆频率。
一种方法是,通过频谱分析得到爆破主振频率f,然后计算错峰减振的微差时间Δt
Δt=1/2f
(6)
另一种方法是,由爆破振动频率f的计算公式,得到微差时间Δt的计算公式
(7)
式中:kf为频率系数,kf=0.01~0.02;cs为岩体中横波。
4.2 半周期减振法与多因素耦合法的应用对比研究
通过频谱分析得到,1.0 kg药量单孔振动波形的主频为92.8 Hz,1.2 kg药量单孔振动波形的主频为57.1 Hz,1.4 kg药量单孔振动波形的主频为92.8 Hz;砂岩的横波波速为914~3 048 m/s。由各半周期减振法计算得到合理微差时间,如表1所示。

表1 半周期错相减振法优选微差时间
由表1可知,由频率计算式(7)计算而得的微差时间为某一范围。1.0 kg、1.2 kg、1.4 kg药量以单孔波形主频计算的微差时间分别为5 ms、9 ms、5 ms,由2.3节得出,掏槽孔数为2~16时,最优微差时间随掏槽孔数而变化。
选择工程中常用方法公式(6)的计算结果,对比半周期错相减振法与多因素耦合法。为定量比较两种方法所选的微差时间差异,计算2~16掏槽孔数下两种方法所选微差时间的最大合成振速差值,如图13所示。

图13 两种方法最大合成振速的差值
由图13可知,在不同掏槽孔数下,1.0 kg药量下两种方法所选微差时间的最大合成振速基本一致,差值小于0.03 cm/s,1.2 kg药量下两者最大合成振速差值较大,普遍大于0.2 cm/s,1.4 kg药量下两者最大合成振速差值与掏槽孔数有关,差值为0~0.15 cm/s。
综上,由于爆破振动波形的复杂性,与多因素耦合法相比,半周期减振法算得的微差时间并不能确保是最优微差时间,甚至可能造成合成振速偏大。因此,当爆破振动控制要求较高时,需要通过多因素耦合法进行精确设计。
5 结 论
(1) 本文提出了精确确定电子雷管隧道爆破参数的多因素耦合法:该方法充分考虑实际爆破振动衰减特性,以单孔爆破振动波形为依据,研究多个爆破参数的复杂耦合关系,利用线性叠加理论和MATLAB编程,计算不同药量、不同孔数、不同孔间延时多种组合下的振动合成曲线,选取最优干扰消振的爆破参数。
(2) 最优微差时间的选取受药量、爆破孔数的影响;同样地,当爆破孔数在某一临界值(本文为16孔)内时,随着微差爆破孔数的变化,最大合成振速值有显著差异;但当超过临界值时,最优微差时间、最大合成振速均将不再受爆破孔数的影响。
(3) 利用多因素耦合法进行观音桥隧道掏槽爆破设计,确定参数如下:8孔逐孔掏槽、掏槽孔药量1.4 kg、孔间延时5 ms。通过掏槽孔和辅助孔的不同孔间延时现场对比试验,验证了多因素耦合法的可靠性;采用该方法确定的参数最大程度实现了爆破振动异向干扰相消,有效控制了爆破振动强度。
(4) 现场应用表明,孔间延时为5 ms时,至第8孔掏槽结束并未形成第二临空面;孔间延时8 ms时,可确定起爆后48 ms已形成了第二临空面。对于短延时(如本文5 ms)掏槽爆破,即使未形成第二临空面,但通过多因素耦合法合理设计短延时,同样可以实现良好的降振效果。
(5) 与多因素耦合法相比,半周期错相减振法算得的孔间延时并不能确保是最优微差时间,甚至可能造成合成振速偏大,如本文中1.2 kg药量下两者最大合成振速差值普遍大于0.2 cm/s。当爆破振动控制要求较高时,需要通过多因素耦合法进行精确设计。
