基于谱元法的车辆-轨道结构频域振动特性研究
2021-03-17吴神花雷晓燕
吴神花,雷晓燕
(华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013)
谱元法(SEM)是一种高精度的频域分析方法[1]。该方法从动力偏微分方程出发,利用傅里叶变换将偏微分方程转换为频域内的常微分方程,通过引入相应的位移边界条件和力边界条件,得到单元谱刚度矩阵。再利用有限元思想,将整体结构离散为若干个单元,并将其组装为整体结构谱刚度矩阵,最后利用虚拟激励法模拟轨道不平顺引起的虚拟激励,通过求解整体结构的谱元法方程得到结构的振动响应。谱元法在结构离散时,单元尺寸的大小对中高频振动计算精度影响甚微,能有效避免有限元法在网格划分较细时带来的计算效率低的问题,同时保持了有限元法对复杂结构适应性强的特点。目前,谱元法不仅可以分析固体结构振动问题[2-3],还可以分析流体力学[4]中的问题,已成功应用于结构振动[5]、地震学[6]和结构损伤识别[7-8]等多个领域,是一种成熟的全频域动力学分析方法,可以为车辆-轨道结构全频域振动噪声分析提供新思路。但将该方法应用于车辆-轨道结构频域振动分析的研究,目前还没有看到。
本文基于谱元法建立车辆-轨道结构频域振动模型,将轨道结构模拟为三层铁木辛柯梁,车辆部分考虑为整车模型,运用Lagrange方程实现车辆与轨道结构的耦合,并运用虚拟激励法将轨道不平顺模拟为虚拟荷载,最后通过求解整体结构的谱元法方程得到车辆-轨道结构全频域振动响应。
1 基于谱元法的车辆-轨道结构振动分析方法
1.1 轨道结构模型
轨道结构模拟为三层铁木辛柯梁单元,如图1所示。其中,钢轨、预制轨道板和混凝土支撑层分别离散为黏弹性点支撑的二维铁木辛柯梁谱单元,钢轨扣件由离散分布的弹簧-阻尼单元模拟,CA砂浆和路基由均布的弹簧-阻尼单元模拟。

图1 无砟轨道结构三层梁谱单元法模型Fig.1 Three layer beam model of ballastless track structure
定义无砟轨道结构三层梁单元的谱结点位移向量为
1.1.1 Timoshenko梁单元谱刚度矩阵
自由振动的Timoshenko梁运动微分方程如下
(1)
式中:G为剪切弹性模量;κ为剪切因子;E为弹性模量;I为横截面的惯性矩;ρ为材料密度;A为梁截面面积;v为梁的垂向位移;φ为弯曲引起的转角。
将垂向位移和转角表示为谱分量的形式
(2)

由式(1)和(2)可得
(3)
设式(3)的一般解为
(4)

将式(4)代入式(3)可以求出波数四个解
(5)
其中:
式(4)的解可表示为
(6)
式(6)前两项表示向右传播的波,后两项表示向左传播的波,l为梁单元长度,其中:
A,B,C,D为待定系数,可通过引入位移边界条件求得,位移边界条件如图2所示。

图2 铁木辛柯梁单元边界位移Fig.2 Boundary displacement of Timoshenko beam element
(7)
通过式(6)和(7)可以求得
(8)
其中
将式(8)代入式(6)可得
(9)

铁木辛柯梁内部弯矩和剪力可以表示为
(10)
将荷载表示为谱分量的形式
(11)
引入铁木辛科梁梁端荷载边界如图3所示。

图3 铁木辛科梁边界荷载Fig.3 Boundary load of Timoshenko beam
(12)
其中S(ω)为铁木辛柯梁谱单元刚度矩阵,可表示为
(13)
其中:
1.1.2 弹簧-阻尼单元谱刚度矩阵
s2=k2+ic2
(14)
式中:k2,c2分别为无砟轨道单元弹簧-阻尼刚度矩阵和阻尼矩阵,公式见参考文献[9];s2为轨道结构弹簧-阻尼单元谱刚度矩阵。
1.1.3 整体谱刚度矩阵
将钢轨、预制轨道板、混凝土支撑层谱单元刚度矩阵以及弹簧-阻尼单元谱刚度矩阵采取对号入座的方式,组装为轨道结构整体谱刚度矩阵Sl(ω)。
1.2 车辆模型
车辆部分模拟为整车模型,车体和转向架考虑沉浮振动和点头振动,车轮考虑沉浮振动,每节钢轨上两个节点考虑竖向位移和转角,整车模型有26个自由度,如图4所示。

图4 整车车辆单元模型Fig.4 Vehicle model
图4中:vci(i=1,2,3,4)为第i个轮轨接触处钢轨竖向位移;vi(i=r1,r2,r3,…,r8)分别表示钢轨第i个节点的垂向位移;θi(i=r1,r2,r3,…,r8)表示钢轨第i个节点的转角。
车辆单元的节点位移向量au,e可以表示为
au,e={vr1θr1vr2θr2vr3θr3vr4θr4vr5θr5vr6θr6vr7θr7vr8θr8θr8vcθcvt1vt2vw1vw2vw3vw4}T
(15)
运用Lagrange方程,可得车辆方程
Muau+Cuau+Kuau=Qu+Qη
(16)
式中:Mu,Cu,Ku分别为车辆单元的刚度、阻尼和质量矩阵;Qu为车辆重力荷载列向量,Qη为轨道不平顺激励,公式如下
(17)
式中:kc为轮轨接触刚度;Nc1,Nc2,Nc3,Nc4为插值矩阵;η1,η2,η3,η4为轨道不平顺,将通过虚拟激励法来模拟。
设不平顺η(t)的功率谱密度函数为Sη(ω),则相应的轨道不平顺虚拟激励为
(18)
由于轨道不平顺功率谱是以空间圆频率表示的单边功率谱,而Sη(ω)为时间功率谱,因此需先将轨道不平顺功率谱转换,时间圆频率ω=βv,β为空间圆频率,v为列车速度,则时间功率谱Sη(ω)为
Sη(ω)=Sη(β)/v
(19)
对于M个轮对情况,有
(20)
式中:η(t)为轨道高低不平顺随机激励历程函数;tj(j=1,2,…M)为各激励点处的激励滞后时间,tj=(aj-a1)/v,aj为t=0时第j个车轮的位置坐标。
与η(t-tj)相应的轨道不平顺虚拟激励为
(21)
对于M个轮对作用情况,式(20)表示为
(22)
其中:
(23)

仅考虑由于轨道不平顺引起的激励,式(16)可变为
Muau+Cuau+Kuau=Qη
(24)
由于轨道高低不平顺为虚拟激励,与此相应的位移响应为
(25)

将式(17)、(22)和(25)代入式(24)可得
(26)

(27)
Su(ω)=(ω2Mu+iωCu+Ku)
(28)
1.3 求解车辆-轨道结构振动响应谱元法方程

(29)
根据虚拟激励法原理,系统结点位移的实际功率谱密度S(ω)为
(30)
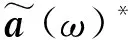
(31)
2 基于谱元法的车辆-轨道结构振动频域分析
采用德国高低不平顺低干扰谱作为轨道不平顺激励,列车速度为250 km/h,线路长度为200 m,轨道单元长度为0.65 m,列车参数和轨道结构参数分别见表1和表2。
2.1 模型验证
图5为0.2~200 Hz内的车体、转向架、车轮垂向加速度功率谱,车体、转向架沉浮加速度的自振频率分别为1 Hz和7.6 Hz,按参考文献[10]公式算出的车体、转向架沉浮加速度的自振频率分别为1.08 Hz和7.9 Hz,可见本文计算结果与参考文献计算结果吻合良好。图5中车体、转向架加速度功率谱谷值处分别对应车辆“定距滤波”和“轴距滤波”频率,与参考文献[11]公式得到的“定距滤波”和“轴距滤波”频率吻合良好,证明了基于谱元法的车辆-轨道结构振动频域分析方法的正确性。
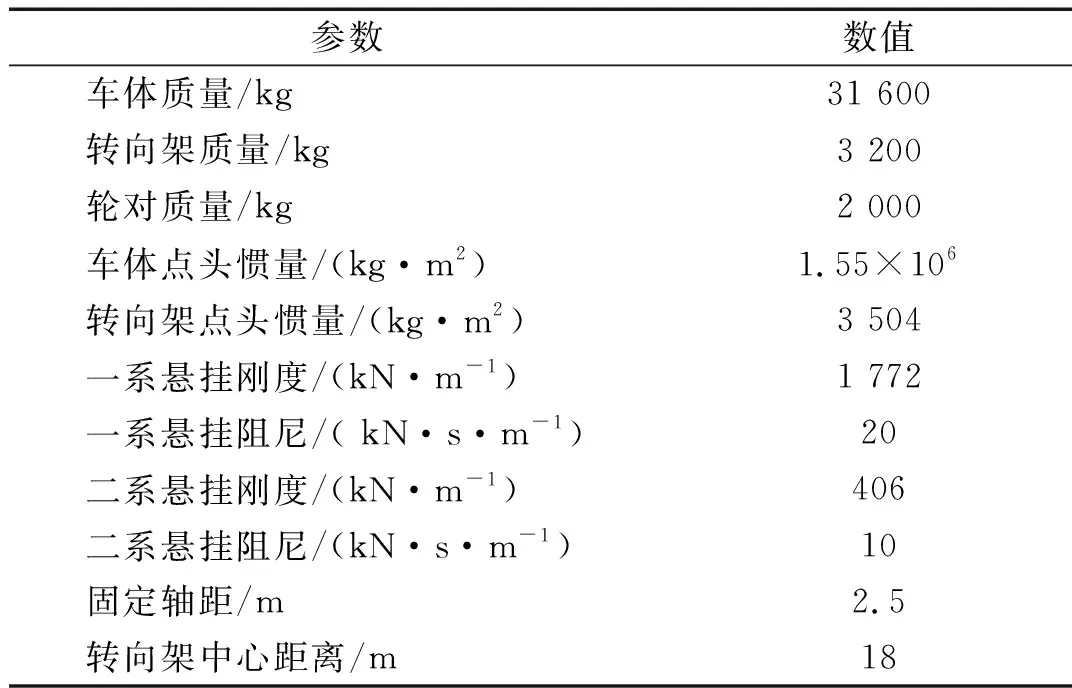
表1 无砟轨道结构参数

表2 高速列车参数

图5 车辆沉浮加速度功率谱
2.2 基于谱元法的车辆-轨道结构振动频域分析
为了得到轨道结构系统的自振频率,不考虑车辆部分,在三层轨道结构系统中间施加一个单位简谐荷载,得到钢轨、轨道板、底座板的垂向位移导纳,如图6所示。由图6可知,钢轨第一、第二阶自振频率为30 Hz、250 Hz,钢轨一阶pinned-pinned频率为1 062 Hz;轨道板和底座板的第一、第二、第三、第四阶自振频率为30 Hz、508 Hz、1 000 Hz、2 839 Hz。

图6 轨道结构垂向位移导纳Fig.6 Vertical displacement admittance of track structure
基于谱元法的车辆-轨道结构振动模型,考虑轨道结构单元尺寸为0.650 0 m、0.375 0 m、0.187 5 m的三种工况,分析车辆-轨道结构频域振动特性。计算结果表明,三种工况下得到的频域振动响应相同,轨道结构单元尺寸大小不会影响计算精度,可见谱元法分析轨道结构中高频振动比有限元法更具优势。以下分析的单元尺寸均为0.650 0 m,图7和8分别为分析频率0.2~200 Hz、1~4 000 Hz内轨道结构垂向加速度功率谱曲线,图9为分析频率1~4 000 Hz内的车辆垂向加速度功率谱曲线。

如图7所示,钢轨、轨道板、底座板的前2阶振动峰值频率为1.1 Hz和8 Hz,分别对应图5中车体、转向架的自振频率;钢轨、轨道板、底座板的第三阶振动峰值频率为28 Hz,对应图6中钢轨、轨道板、底座板的一阶自振频率;钢轨、轨道板、底座板的第四阶峰值频率对应图5中车轮自振频率。综上可见,钢轨、轨道板、底座板前2阶振动峰值由车体、转向架自振产生,第三阶峰值频率由轨道结构系统自振产生,第四阶峰值频率由车轮自振产生。
由图8可知,钢轨、轨道板和底座板的振动在28 Hz、504 Hz和2 660 Hz处有峰值,分别对应图6中轨道结构系统一阶自振频率、轨道板和底座板的第二、第四阶自振频率,说明轨道结构系统的这几处峰值都是由轨道结构系统自振引起的;而钢轨另一处峰值在1 166 Hz处,轨道板和底座板在922 Hz处,这也是对应图6中轨道板第三阶自振频率,可见此处峰值是由轨道结构系统自振产生的,而钢轨、轨道板和底座板的峰值频率之间的差异是由于图6中钢轨的pinned-pinned振动导致的。
由图8还可以看到,在全频域内钢轨振动远远大于轨道板和底座板的振动,说明钢轨扣件在全频域内具有良好的减振效果;在频率小于500 Hz时,轨道板和底座板加速度功率谱相同,说明小于500 Hz时,CA砂浆无减振作用;但大于500 Hz时,轨道板振动远大于底座板的振动,说明高频振动衰减快。
由图9可知,车体和转向架的加速度功率谱对应的谷值处频率符合“车辆几何滤波效应,由图9可见,转向架的自振频率为7.6 Hz,当频率大于转向架自振频率时,车轮振动大于车体和转向架的振动,说明一、二系悬挂减振具有良好的效果。在频率为500 Hz时,车轮的加速度功率谱也有峰值,与下部轨道结构对应的峰值频率相同,说明该峰值也是由轨道结构系统自振引起的。
2.3 轮轨接触处车辆-轨道结构系统的振动响应
车辆-轮轨耦合系统包含了一节车厢四个轮轨接触激励,图10和11分别为四个车轮作用处车轮、钢轨加速度功率谱曲线。

图10 四个车轮加速度功率谱Fig.10 Acceleration power spectrum of four wheels
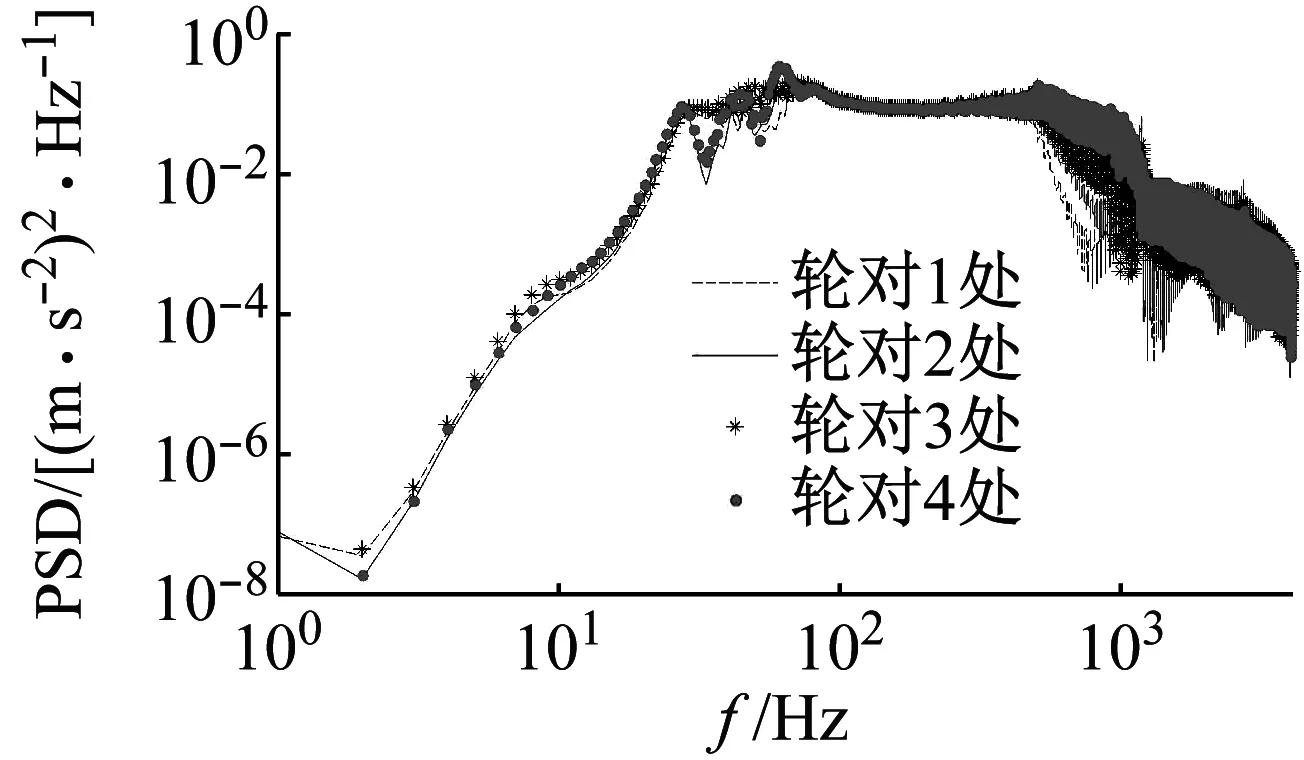
图11 四个轮对处钢轨加速度功率谱Fig.11 Acceleration power spectrum of rail at four wheelsets
由图10可知:在小于25 Hz、大于1 000 Hz和80~1 000 Hz内,四个车轮振动相同;在20~80 Hz内,四个车轮峰值不同;在120~500 Hz内,车轮4振动最大,在400~1 000 Hz内,车轮1振动最大;四个车轮均在500 Hz处有峰值,这是由轨道结构系统自振引起。
由图11可知,在小于25 Hz和80~500 Hz内,钢轨振动在四个轮对作用处振动相差不大;在25~80 Hz内,钢轨的振动峰值有差异,与图10对应车轮振动峰值相同,说明该频域内主要受车轮自振的影响较大;在500~1 000 Hz内,钢轨振动大小关系为:车轮4处>车轮3处>车轮2处>车轮1处;大于1 000 Hz时,钢轨振动大小关系为:车轮4处<车轮3处<车轮2处<车轮1处。
2.4 远离车辆一侧沿钢轨方向轨道结构振动响应
图12和13为远离车辆一侧且距离端轮对0、2.5 m、18.0 m、20.5 m处钢轨、轨道板振动加速度功率谱曲线。由图12可知,在距离端轮对2.5 m处,1~800 Hz内钢轨振动迅速衰减,当大于800 Hz时,钢轨振动衰减不大;在距离端轮对18.0 m与20.5 m处,25~1 171 Hz内的钢轨振动基本相同,说明距离端轮对18.0 m处,钢轨振动衰减基本稳定;在距离端轮对20.5 m处,小于25 Hz时,钢轨振动随着离开端轮对距离的增加迅速衰减,衰减幅值超过了103倍,当大于1 171 Hz时钢轨振动则衰减较小。由图13可知:在1~25 Hz与500~2 000 Hz内轨道板振动距端轮对越远而衰减越大;在25~500 Hz和大于2 000 Hz内,轨道板振动衰减甚微,基本趋于稳定。

图12 钢轨加速度功率谱Fig.12 Acceleration power spectrum of rail

图13 轨道板加速度功率谱Fig.13 Acceleration power spectrum of track plate
3 结 论
本文基于谱元法建立了车辆-轨道结构振动频域分析模型,运用虚拟激励法将轨道不平顺模拟为虚拟荷载,运用Lagrange方程实现车辆与轨道结构的耦合,从而建立车辆-轨道结构的整体谱元法方程。利用该方法,分析了车辆-轨道结构在频域内的振动响应,得到以下结论:
(1) 钢轨、轨道板和底座板的第一、第二、第四阶振动峰值分别由车体、转向架、车轮自振引起;其他振动峰值由轨道结构系统自振引起。钢轨、轨道板和底座板的振动能量分布在较宽的频率范围。
(2) 钢轨扣件在全频域内具有良好的减振效果;由于CA砂浆的刚度比较大,CA砂浆层对轨道结构的减振作用不明显。
(3) 远离车辆一侧且距离端轮对2.5 m处,1~800 Hz内钢轨振动迅速衰减,当大于800 Hz时,钢轨振动衰减不大;在距离端轮对18.0 m处,25~1 171 Hz内的钢轨振动衰减基本稳定;在距离端轮对20.5 m处,小于25 Hz时,钢轨振动随着离开端轮对距离的增加迅速衰减,衰减幅值超过了103倍,当大于1 171 Hz时,钢轨振动则衰减较小;在1~25 Hz与500~2 000 Hz内,轨道板振动距端轮对越远衰减越大。
(4) 基于谱元法的车辆-轨道结构振动分析方法具有计算速度快、计算精度高的特点,为车辆-轨道耦合系统结构振动全频域分析提供了一种新方法。
