基于EDFT的非均匀欠采样叶尖定时信号分析
2021-03-17张继旺丁克勤
张继旺,丁克勤
(中国特种设备检测研究院,北京 100029)
高速旋转叶片是烟气轮机、压缩机、航空发动机等大型透平机械的核心部件,由于长期在极端载荷环境下运行,很容易产生疲劳失效[1-4],进而发展为断裂事故,造成灾难性的后果。因此,对旋转叶片的运行状态进行在线监测,在叶片失效前及时采取有效措施,对保障设备安全运行具有重要意义。但由于旋转叶片结构和运行工况的特殊性给其状态监测带来很大挑战。截止目前,在众多潜在的叶尖定时监测技术中,叶尖定时技术因其非接触、非侵入性及只需少量传感器就可同时监测所有叶片的振动信息的优势,成为最具潜力的旋转叶片监测技术,得到领域内相关学者和工程人员大量关注和研究[5-8]。该方法是通过安装在旋转叶片外围机壳上的定时传感器来记录叶片到达的时刻,再与无振动时进行对比,从而间接测取旋转叶片振动幅值信息。然而,由于该技术单传感器的采样频率一般远低于叶片振动频率,使得所测得的信号属于严重的欠采样信号,多个传感器时又受限于设备的结构特点无法均匀布置,使得多传感器的采样频率为非均匀采样。导致以采样定理为基础的经典傅里叶变换无法对所采集到的叶尖定时信号进行有效处理,也就难以从叶尖定时信号中得到叶片振动的谱信息。
针对这一问题,国内外相关学者开展了大量研究,如李孟麟等[9]研究了基于旋转不变子空间法的欠采样叶尖定时信号频率估计,对理想无噪声干扰条件下的采样信号结果具有较好的辨识效果。贺长波等[10]在此基础上继续探究了基于总体最小二乘准则(TLS)的旋转不变子空间法(Esprit)对存在噪声干扰的欠采样信号进行频率估计,并以估计结果作为先验知识对欠采样信号进行重构。Hu等[11]提出了一种基于三角函数插值的欠采样信号重构方法,仅利用两个叶尖定时传感器实现了叶片振动信号的重构,但该方法需要一定的先验知识作为支撑,在实际应用中较为困难。郭浩天等[12]针对传统单参数法无法实现叶片共振倍频数辨识的问题,研究了一种基于多传感器的叶片共振倍频数测量方法,实现了叶片共振倍频数辨识。Lin等[13]针对叶片多模态振动下所采集的叶尖定时信号,构造了欠采样信号稀疏表征模型,并通过压缩感知的方法求解了叶片的振动频率,该方法在满足定时传感器数量要求下对仿真信号及试验数据均取得了较好的效果。张效溥等[14]研究了叶片振动特性,并提出了传感器任意排布下基于压缩感知的叶尖定时信号重构方法。Bouchain等[15]针对叶尖定时信号的欠采样问题提出了一种基于l0-正则化的OMP处理方法,解决了一定条件下的叶尖定时信号的欠采样处理问题。上述研究对叶尖定时信号分析有很大推动,在一定程度上能解决了叶尖定时非均匀采样或欠采样谱分析的问题,但可以看出这些方法有的只解决了二者中的一个问题,或者是在分析中需要较多的先验信息支撑,再者就是只能解决特定约束条件下的问题,故在实际应用中有一定的限制。为了更好的解决叶尖定时信号非均匀采样和欠采样性导致的谱分析难题,本文提出了基于扩展离散傅里叶变换的非均匀欠采样叶尖定时信号分析方法,从而实现叶片振动参数的辨识。
1 叶尖定时测振原理简介
叶尖定时测振基本原理如图1所示,通过在旋转叶片外围机壳上安装若干个定时传感器(如图中探头1、2、3),来记录叶片在旋转过程中到达这些传感器的时间,在转轴处安装键相传感器S用于转速计算。当叶片旋转过程中产生振动,叶尖到达定时传感器的时间会提前或滞后于理论时间,从而产生一个时间差,再据该时刻对应的转速信息可计算出叶片振动位移[16],计算方程如式(1)所示。通过连续采集即可得到叶片振动位移序列,再利用不同的分析算法对该振动位移序列进行处理,即可得到叶片的振动信息。


图1 叶尖定时测振原理Fig.1 Blade tip timing vibration measurement principley=Δt·V
(1)
式中:y表示叶片振动位移;Δt表示因振动产生的时间差;V表示叶尖通过定时传感器时的周向线速度。由叶尖定时测振原理可以看出单个定时传感器的采样频率为转频,而叶片振动频率一般又远高于转频,所以所测得的叶尖定时信号属于严重的欠采样信号。为了提高采样频率,一般会安装多个叶尖定时传感器,即叶片旋转一周会测得多个叶片振动数据,将这些不同传感器所测得的数据进行插值整合,来提高叶尖定时信号的采样率,但由于设备结构限制,一般可安装的传感器数量也有限,且这些传感器无法均匀分布在机匣上,这就导致最终所获取的信号不仅欠采样,而且还属于非均匀采样。这时这种严重的非均匀欠采样的信号就不再满足奈奎斯特采样定理,使得基于传统傅里叶变换的谱分析方法不再适用,给叶片振动参数辨识带来挑战。
2 扩展傅里叶变换方法
2.1 理论基础
采用经典的傅里叶变换进行信号的谱分析时,需严格满足奈奎斯特采样定理要求,即采样频率大于2倍的分析频率,且为均匀采样,而叶尖定时信号即非均匀采样,更是严重的欠采样,这就使得传统的傅里叶变换难以有效的对叶尖定时信号进行谱分析。
为了解决严重的非均匀欠采样信号分析处理的问题,提出了一种扩展傅里叶变换处理算法,不同于传统的傅里叶变换,扩展傅里叶变换的基本思想是以傅里叶积分变换为目标,对有限带宽信号在扩展的频率范围内构造一个变换基,将原始数据通过迭代拟合使其在欧几里德范数上接近傅里叶变换结果[17],具体推导过程如下:
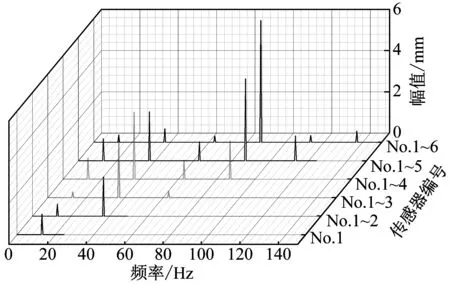
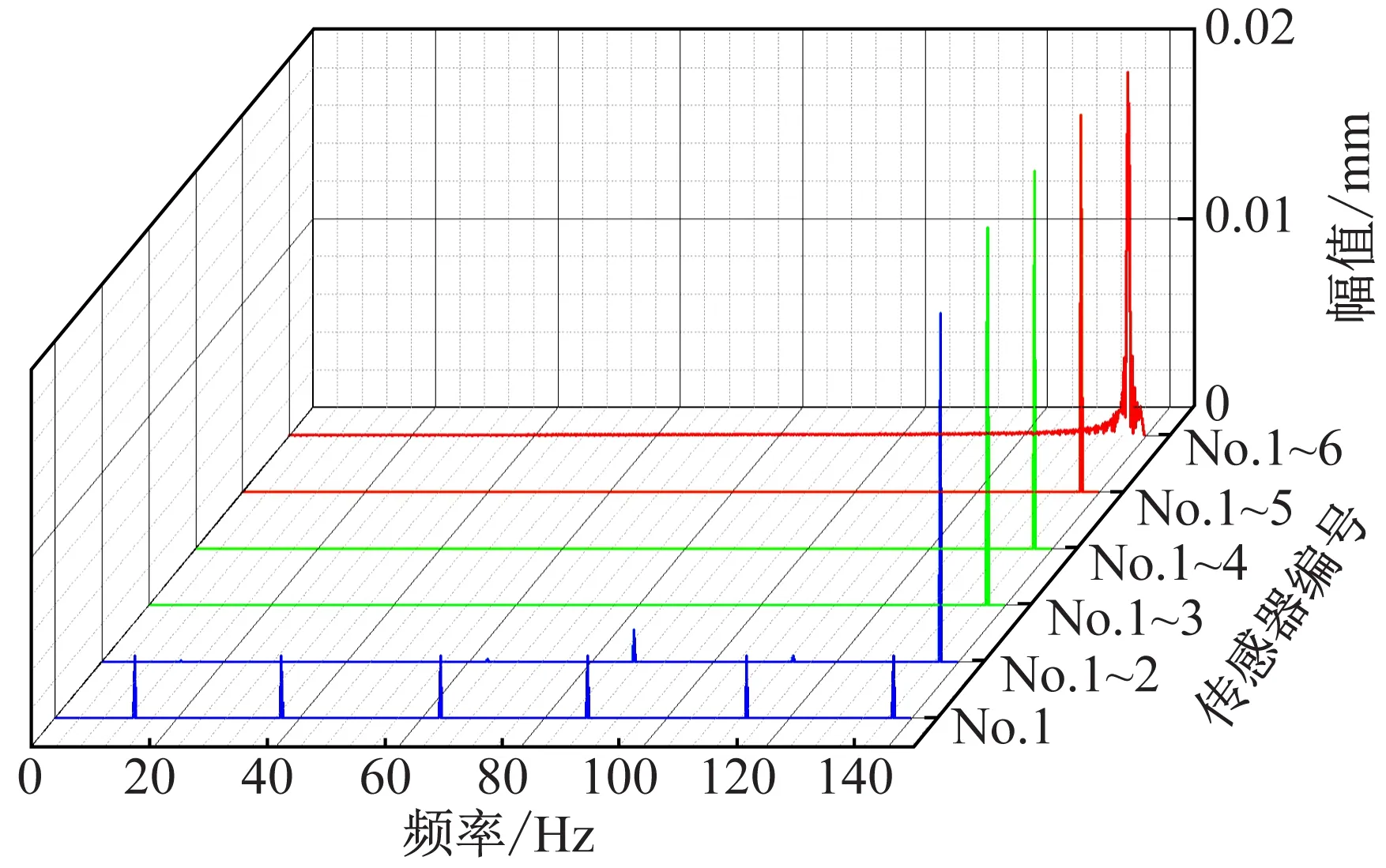
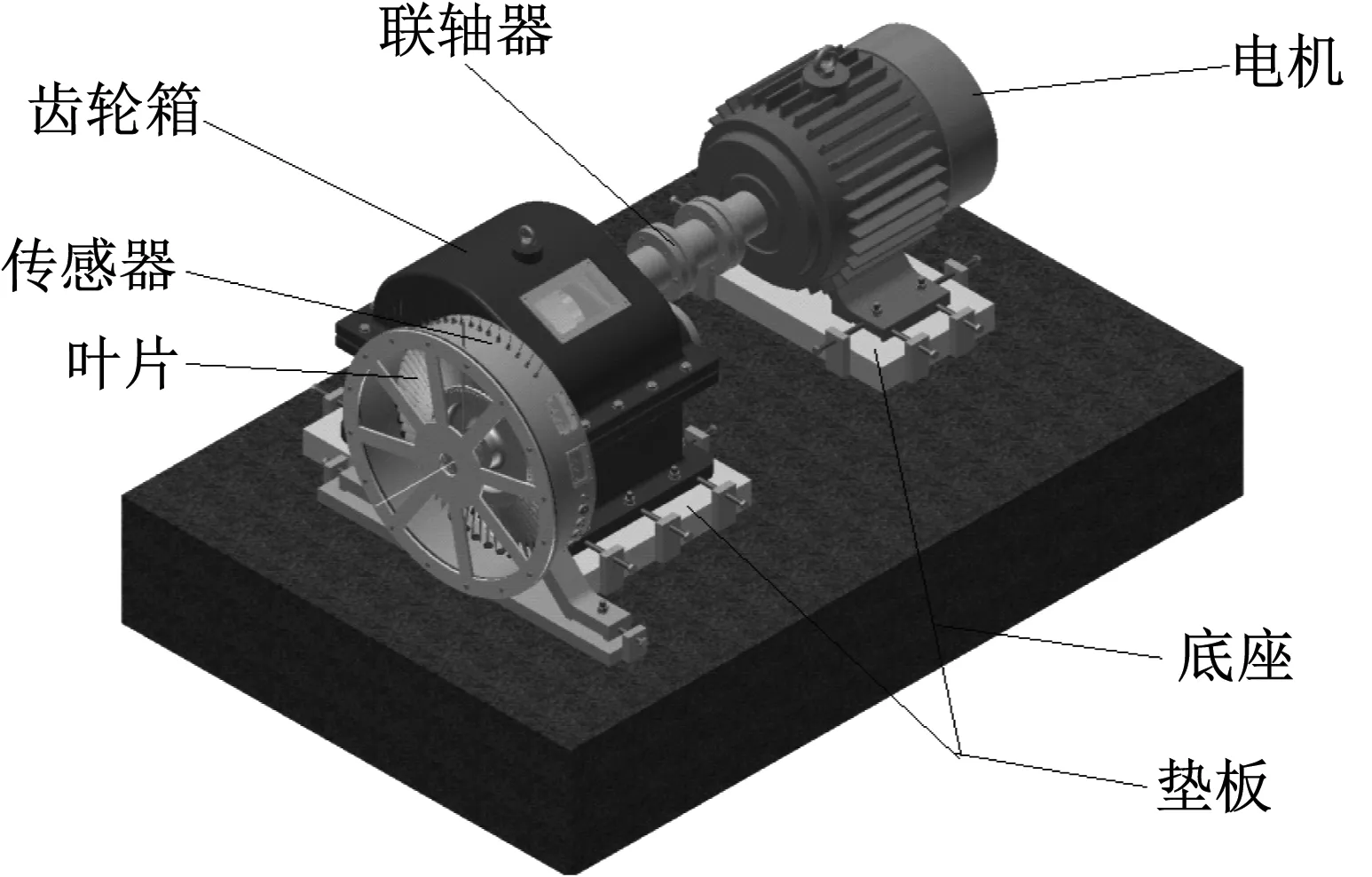
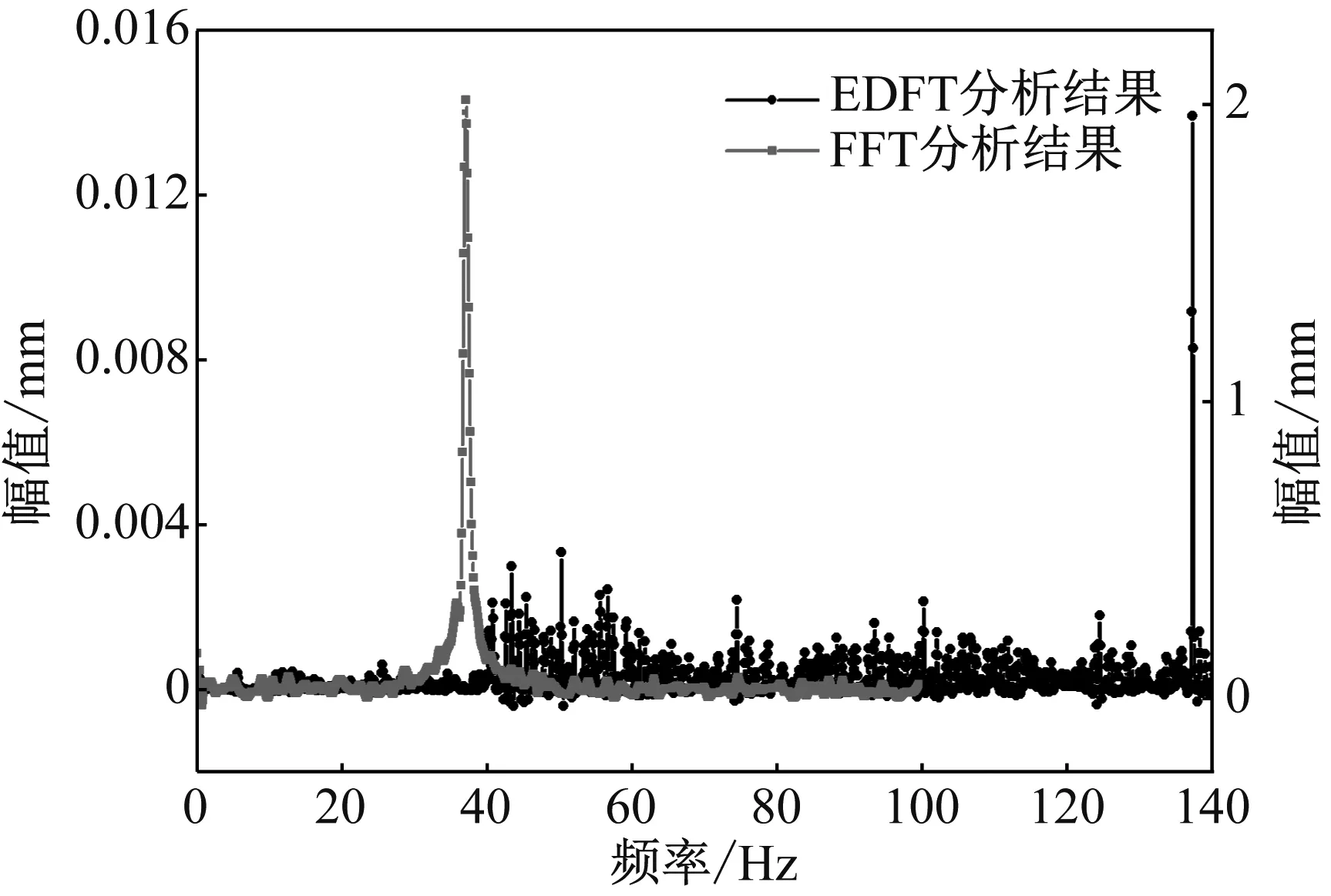
对有限频带范围(-Θ/2 (2) 用所构造的优化变换基α(ω,t)代替传统傅里叶变换的基e-jωt,则扩展傅里叶变换的基本表达式如式(3)所示 (3) 对于非均匀离散采样信号,将采样幅值序列表示为x(tk),采样时间序列表示为tk,k=0,1,2,…,K-1,K是采样长度,则对于非均匀采样信号的EDFT计算式如式(4)所示 (4) 为了使F(ω)与Fα(ω)接近,需构造函数 (5) 然而,对于带限信号F(ω)直接求取是困难的,为使式(5)成立必须找一个表达式来替代,考虑在无限的时间间隔里用圆频率ω0和幅值谱S(ω0)来表示x(t),δ为狄拉克函数,则FFT变换可以表示如式(6)所示 (6) 对于有限带宽信号的频带范围[-Ω,Ω]内的幅值谱S(ω0)已知的信号,其最小二乘误差估计的积分可以表示为式(7a),对于非均匀离散采样信号则可以表示为式(7b)(后续仅对离散采样信号进行讨论)。 对式(7b)进行求解即可构造一个EDFT分析的基函数,其中,为了确定S(ω0)与时间序列x(tk)对应的幅值谱Sα(ω),当Δ=0,ω=ω0时,定义Sα(ω)如式(8)所示 (8) (9) (10) (11) 再将式(11)代入式(3)和式(8)中,即可得到EDFT的解如式(12)和式(13)所示 (12) (13) 式中:矩阵E为K×N的指数矩阵,各元素为Ek,n=e-j2πfntk;矩阵R为向量x(tk)的自相关矩阵,是一个K×K的Hermit矩阵,R中各元素计算式如式(14)所示 (14) 由此,实现了扩展傅里叶变换的求解,由上述求解过程可以看出,EDFT相对于传统的FFT分析,不再受奈奎斯特采样定理的限制,扩大了分析频率范围,分析谱线数同样不再受限于采样点数,提高了频率分辨率。EDFT能够解决非均匀采样和欠采样信号谱分析的难题,为叶尖定时信号的分析和参数辨识提供了可行的方法。 对于一个有限带宽[-Ω,Ω]内的信号,其离散的频率值为-Ω≤ωn<Ω,n=0,1,2,…,N-1;对应的时域采样数据为x(tk),k=0,1,2,…,K-1,且N≥K。则扩展傅里叶变换具体计算过程: Step1:功率谱向量初始值设为W0=[1,1,…,1]1×N; Step2:根据W0的初始值来确定自相关矩阵R1; Step3:计算傅里叶变换F(1)、离散幅值谱S(1)、功率谱W(1),为下一次迭代做准备。 Step4:进行F(i)、S(i)、W(i)循环迭代,当迭代最大次数I达到或功率谱变化率小于所给定的阈值时迭代将会终止。 Step5:输出,得到扩展傅里叶变换谱信号。 其中自相关矩阵R(i)计算式如式(15)所示 (15) EDFT算法的输出如式(16)所示 F(i)=x(R(i))-1EW(i) (16) 幅值谱计算式如(17)所示 (17) 功率谱向量计算式如式(18)所示 (18) 迭代阈值计算式如式(19)所示 (19) 其中,i为迭代次数,i=1,2,…,I。 由EDFT算法可知,该算法输入参数仅有: t:信号采样时间序列; x:信号采样数据; I:迭代次数; f:分析频率序列,f需满足length(f)>length(x),且具有关于0对称的正负频率。 由文献[18-20]可知,旋转叶片的低阶振动可认为是简谐振动,故构造叶片振动信号y(t)表达方程如式(20)所示 y(t)=A·sin(2π·ft) (20) 式中:A为叶尖振动幅值;f为振动频率。以实验室所搭建试验台(见3.2节)叶片测试数据为基准,设A=0.02 mm,f=137 Hz。 由于单个定时传感器的采样频率为转频Fr,则n个传感器采样频率则为nFr(同步采样可能性较低,这里暂不讨论)。假设叶轮转速为3 000 r/min,则单传感器采样频率为50 Hz,远小于137 Hz,属于严重的欠采样,若想满足采样定理,则至少需要6个均匀分布的定时传感器。考虑实际设备中均匀分布是不可能的,因此假定叶轮半个周向区域内安装有6个定时传感器,传感器两两相隔36°,由于不是均匀分布,所以这些传感器的采样信号是非均匀采样,且当选择小于6个传感器的采样数据时,即得到的信号接近于实际采样的非均匀欠采样的信号。为了便于计算,规定叶片第一次到达1号传感器时为0时刻,这样6个传感器就可以得到6组单独的采样数据,每组数据的采样时间间隔Δt=1/Fr=0.02 s,选取单个传感器采样点为K=100,那么对于第j个传感器来说,其理想状态下采样时间序列如式(21)所示。考虑到实际系统测量中存在定时误差和系统测量误差[21],定时误差主要由于传感器和系统的响应速度有关,长周期采样结果应符合随机误差特性,故在采样时间序列中加入均值为0,信噪比强度为d的随机误差,则定时误差的采样时间序列如式(22)所示;而系统测量误差则是由系统测量精度决定,其同样应该满足随机误差特性,本文在理想采样基础上加入均值为0,一定幅值的随机误差来表示。 uj=[0+0.002(j-1),0.02+0.002(j-1), 0.04+0.002(j-1),…,1.98+0.002(j-1)]T (21) uj′=awgn(uj′,d) (22) 其中,j=1,2,3,4,5,6,表示传感器的编号,则理想状态、含有定时误差和含有测量误差下的每个传感器采样得到的叶片振动位移序列如式(23a)、式(23b)和式(23c)所示 yj=0.02sin(2π·137uj) (23a) yj′=0.02sin(2π·137uj′) (23b) yj″=yj+h·rand(length(y),1) (23c) 式(23a)表示理想状态下的采样信号,式(23b)表示仅含有定时误差下的采样信号,式(23b)表示含有系统测量误差的采样信号,也更接近于实际工况下含有定时测量误差的采样信号,其中h表示误差幅值大小。 对不同传感器组合的数据进行分析时只需对所选传感器的振动数据按照编号进行插值处理即可,当传感器数量大于1时,所得数据均为非均匀采样信号。 首先对理想采样状态下不同数量传感器仿真数据进行传统傅里叶变换(FFT),得到不同传感器数量下对应的时域(time-domain,T-D)信号和传统FFT变换后的频域(frequency-domain,F-D)信号分别如图2和图3所示。 图2 不同数量传感器所采集的时域信号Fig.2 T-D signal collected by different number sensors 由图3可以看出,仅对1个传感器的采样数据进行FFT分析,只在13 Hz处出现峰值,这与实际振动频率137 Hz相差较大;当传感器数量逐渐增多时,频域图中出现多组成分,且当传感器数量达到6个时,基于FFT分析的频谱图中出现叶片振动频率成分,幅值为0.55 mm,远小于其它成分幅值,且不等于叶片实际振动幅值,这主要是由于采用6个传感器进行采样虽然达到了FFT分析中采样频率的要求,但该信号并不满足均匀采样的要求,造成FFT分析时发生频率偏移和混叠。综上所述,传统的FFT变换难以对非均匀欠采样的叶尖定时信号进行有效的分析处理。 图3 不同数量传感器采样信号的频域图(传统FFT)Fig.3 F-D diagram of different number of sensors (traditional FFT) 对理想采样状态下不同数量传感器的仿真数据进行扩展离散傅里叶变换(EDFT)处理,分析频率序列为f=-140∶0.2∶139.8,迭代次数I取15,得到不同传感器数量下对应的频域信号如图4所示(取正半轴数据)。 图4 不同数量传感器采样信号的频域图(传统EDFT)Fig.4 F-D diagram of different number of sensors (EDFT) 由图4可以看出,仅对1个传感器的数据进行EDFT分析,就出现了叶片振动频率成分,只是频谱图中出现多组谐波成分;当传感器数量为2时,频率主要成分为叶片振动频率,幅值为0.019 mm,已基本等于真值;当传感器数量大于等于3时,频率中干扰成分基本消失,幅值等于真值0.02 mm;表明当采样率达到一定要求后,基于所提方法能够准确分析得到非均匀欠采样信号的频域成分,实现理想采样状态下叶片振动参数的有效辨识。 考虑实际采样中存在的定时误差情况,对3个传感器状态下的定时时间信号中分别加入信噪比为10、20、30和40 dB的噪声信号,得到仅含有定时误差的采样信号,基于EDFT变换分析结果如图5所示。 图5 不同定时误差下基于EDFT的频域图Fig.5 F-D diagram based on EDFT under different timing errors 由图5可以看出,对于仅有含定时误差的非均匀欠采样叶尖定时信号,通过EDFT分析得到的频率成分为137 Hz,幅值为0.02 mm,即为叶片的真实振动参数,且未产生其它干扰成分,表明采用EDFT方法可以对仅含定时误差的叶尖定时信号进行有效分析,且具有非常良好的抗干扰性。 然后考虑实际采样中存在系统测量误差情况,对3个传感器状态下含系统测量误差的采样数据进行分析,通过在理想采样信号中分别加入最大幅值为0.25 A、0.50 A、0.75 A和1.00 A的随机噪声来构造系统不同的测量误差下的采用信号,对其进行EDFT分析,结果如图6所示。 图6 不同系统测量误差下基于EDFT的频域图Fig.6 F-D diagram based on EDFT under different measuring errors 由图6可以看出,对于含不同强度随机测量误差的叶尖定时信号,采用EDFT分析得到的主要频率成分均为叶片真实振动频率137 Hz,对应的幅值范围在0.019 3~0.019 9 mm,基本等于真值,分析结果中在0 Hz处出现幅值较大的一组成分,这是由于随机噪声所引起的,并不影响对叶片振动参数的分析。表明EDFT方法对含有随机测量误差的叶尖定时信号分析具有良好的可靠性和抗干扰性。 由上述仿真信号分析结果可以看出,采用EDFT方法可以对非均匀欠采样叶尖定时信号进行有效分析,能够实现叶片振动参数的准确辨识,且具有良好的鲁棒性。 为进一步验证所提方法的有效性,搭建如图7所示的测试试验台,测试叶片如图8所示,对实测叶尖定时信号进行分析。该试验台由底座,电机,叶轮,叶片(外径300 mm)、护罩等部件组成,叶尖定时传感器选用光纤传感器,原始脉冲信号的采样频率为100 MHz,4个传感器以相邻25°的角度安装在叶轮护罩上。为了验证分析结果的准确性,采用有限元模拟,得到该叶片一阶振动频率为137.2 Hz,振动幅值为0.014 mm。 图7 测试试验台示意图Fig.7 Schematic diagram of test bench 图8 试验叶片Fig.8 Experimental blade 对所测得的叶尖定时信号进行FFT分析和EDFT分析,其中进行EDFT分析时,迭代次数设为15,分析频率序列范围为(-140,139.8),频率分辨率同样取0.2 Hz,所得到的频域信号分别如图9所示。 图9 实测叶尖定时信号FFT和EDFT分析对比Fig.9 Comparison of FFT and EDFT analysis for BTT signals 由图9可以看出,对实测叶尖定时信号进行FFT分析,其频率主要成分为39 Hz,幅值为2.1 mm,二者均不能反映叶片真实的振动参数;而基于EDFT分析,其频率主要成分为137.0 Hz,幅值为0.013 mm,与叶片实际振动参数基本相同。表明基于所提出的EDFT分析方法能够对实测的非均匀欠采样叶尖定时信号进行准确分析,实现叶片振动参数的有效辨识,具有良好的实用性。 论文针对叶尖定时信号因严重的非均匀采样和欠采样导致的谱分析难题进行了相关研究,所得主要结论如下: (1) 提出了基于扩展傅里叶变换的非均匀欠采样叶尖定时信号分析方法,突破了传统FFT分析中需严格满足采样定理的限制,扩大了分析频率范围,提高了频率分辨率。 (2) 建立了非均匀欠采样叶尖定时系统采样过程的数学模型,推导了多传感器状态下的叶尖定时信号采样方程,为叶尖定时系统数值仿真提供了新思路。 (3) 最后,采用仿真信号和试验测试信号对所提出的EDFT分析方法进行了可行性和有效性验证,结果表明EDFT方法可以有效解决非均匀欠采样叶尖定时信号的谱分析难题,且该方法具有良好的抗干扰性和实用性。

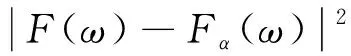
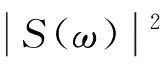

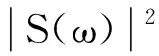
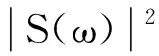
2.2 算法实现

3 方法验证
3.1 仿真信号验证



3.2 试验验证

4 结 论
