沉降室升降阀板的气固两相流场数值分析

徐建华，杨立山，陈 亮，陈 辉，丁桐桐

（中联重科股份有限公司国家混凝土机械工程技术研究中心，湖南长沙410205）

近些年紧随着国家环保战略，采用机制砂替代江海河砂的趋势愈来愈明显，越来越多的机制砂成套系统设备涌现出来。其中，砂石骨料的级配参数是决定砂石品质是否符合国家标准的重要依据。为了满足工程要求，实现环保清洁生产线，在制砂线中引进了风选沉降系统。其中，风选沉降系统主要由风选箱、沉降室、除尘室和除尘管道等组成。砂石骨料从前端进入到风选箱，在空气负压作用下将粒径较小的砂石颗粒输送到沉降室中，在沉降室中经过选择性沉降实现砂石骨料的级配调整，其升降阀板对沉降粒径的调整起到关键性作用。

目前沉降室的研究有：三维定常流动惯性沉降颗粒分离［1］；采用重力沉降原理在复杂浆泵中消除固体颗粒杂质［2］；气固两相流分析喷丸效果和道路清扫车降尘效果［3-5］。以上计算分别采用了重力沉降和惯性沉降的方法对颗粒进行了研究，但未综合考虑应用惯性沉降和重力沉降的方法进行研究。本文以计算流体力学作为基础，重点研究在惯性和重力双重沉降效果下，升降阀板的长度对沉降室气相流场、砂石颗粒的运动轨迹、颗粒沉降效率和系统阻力的影响。

1 仿真模型

在机制砂风选沉降系统中通过气流带动颗粒运动，属于在定常、恒温、不可压缩气体下的流固双向耦合环境。在目前流固耦合计算中有3种方法：Euler-Euler方法将流体和固体皆视为连续相考虑；Lagrange-Lagrange方法将流体和固体都用离散相进行分析；Euler-Lagrange方法将流体作为连续相，固体颗粒作为离散相分析，更加切合实际工况的要求。因此，需要分别采用气相和固相模型进行计算［6］。

1.1 气相湍流模型

为了能更加准确地拟合砂石颗粒在系统中的运动轨迹，气相流场采用湍流模型，Realizablek-ε模型采用新的湍流黏度公式，ε方程从涡量扰动量均方根的精确运输方程推导出来，可以精确地模拟砂石颗粒的射流扩散问题，在旋转流计算、带方向压强梯度的边界层计算和分离流计算问题中更加符合真实工况［7-9］。

Realizablek-ε模型关于湍流动能k和湍流耗散率ε的输送方程如下：

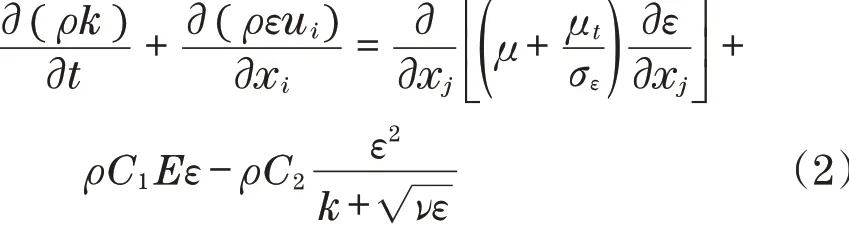
式中：ui为平均速度分量；xi、xj为坐标变量；ρ为流体密度；ν为运动黏度；E为时均应变率；σk=1.0；σε=为由平均速度梯度引起的湍流动能k的产生项，

式中：μt为湍流黏度，表达式为

1.2 颗粒运动轨迹模型

砂石颗粒占整个流场的体积分数小于1%，使用基于Euler-Lagrange方法的离散相模型（DMP）计算最为合适。在笛卡尔坐标系下，单个颗粒的运动轨迹由自身的重力、流体对颗粒的黏性曳力、动压托力决定，颗粒的作用力平衡方程为

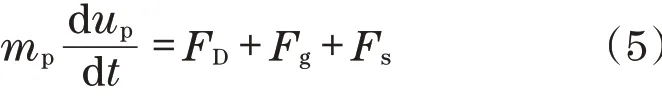
式中：FD为流体对颗粒的黏性曳力；Fg为颗粒重力；Fs为流体对颗粒的动压托力；mp为颗粒质量；up为颗粒速度。

1.3 风选沉降系统模型和网格划分

本文采用Pro-E 5.0建立风选沉降系统物理模型，其中，风选箱由砂石物料入口、物料出口、上进风口、左进风口和多级扬料板等组成，沉降室由砂石颗粒进风管、升降阀板、右转动阀板、出风口、固定阀板、沉降口、补风口等组成，然后通过管道将两者连接，沉降室结构如图1所示。对模型进行网格划分，在边界条件、结构细微处、流场计算量大处进行多层加密处理，共有4 000 000个网格单元，满足计算要求，风选沉降系统网格化模型如图2所示。

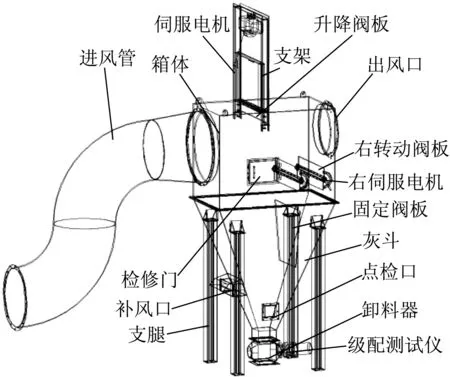
图1 沉降室Fig.1 Settlement chamber

图2 沉降系统网格模型Fig.2 Sedimentation system mesh model

气相流场边界条件设置如下：风选箱物料入口、上进风口、左进风口、物料出口边界条件都采用压力进口，压力大小为标准大气压；沉降室出风口采用速度入口边界条件，根据出口管道直径为850 mm，风机风量60 000 m3/h，得到出口速度大小为-21.2 m/s；沉降室沉降口和其他区域采用壁面边界条件，壁面的法向和切向动量传递系数分别为0.90和0.85。

颗粒相边界条件设置如下：颗粒材质定为花岗岩，密度为2 800 kg/m3；为了防止颗粒与气流发生速度分离，颗粒的入口速度与气流速度相等为5 m/s；从风选箱入口喷射5组Rosin-Rammler分布的颗粒源，不同粒径颗粒进料级配如表1所示。设定计算时间步长为5×10-5s，每个时间步迭代步数为50，先计算气相流场，待气相流场稳定后再进行气固两相流和流固耦合计算。

表1 风选箱进料级配Tab.1 Classifier feeding gradation

2 仿真结果与分析

采用相同的物理模型、边界条件和求解方法，设定升降阀板的长度L分别为400、600、800、1 000 mm，研究升降阀板长度对沉降室速度压力场、颗粒运动轨迹、沉降性能和设备阻力的影响，以及气相压力对沉降室的作用效果。

2.1 升降阀板对速度场和压力场的影响

图3 为在相同的计算条件下，不同升降阀板长度时沉降室气相流场的速度云图。通过对比可以看出：当L=400 mm时，气流在沉降室进风口和出风口处的速度大小基本相同，且在出风口管道内速度大小呈均匀分布，并未发生减小，对升降阀板与右转动阀板的磨损较小；当L=600 mm时，气流随着升降阀板的增长向下流动，在出风管的底部位置流速明显降低，同时在出风管的中心位置速度增大，有助于颗粒在此处与气流产生速度分离，产生沉降；当L=800 mm时，在灰斗固定阀板位置速度明显增大，部分颗粒在此处将会被二次吹起，部分小粒径颗粒被选出；当L=1 000 mm时，升降阀板左右两侧区域速度明显减小，在固定阀板两侧形成了两股气流，两股气流先在右转动阀板发生挤压碰撞，然后在升降阀板处与右转动阀板间形成了狭长的高速气流带，气流强度明显增大，沉降室的阻力也同时增大。

图4 为在相同的计算条件下，不同升降阀板长度下沉降室气相流场的压力云图。可以看出，随着升降阀板长度的增加，气流通过升降阀板与右转动阀板间的流通面积将会逐渐减小，在沉降室出风管处的压阻逐渐增大。其中，当L=400 mm时，整个沉降室内的压阻基本相同，约为800 Pa；当L=600 mm时出风管的压阻显著增大，达到1 800 Pa，压力发生质的变化，颗粒的运动轨迹将随着压力的增大发生改变，从气流中脱离出来。

2.2 升降阀板对颗粒运动轨迹的影响

图5 为在相同的计算条件下，不同升降阀板长度下粒径45～75μm颗粒运动轨迹。通过对比可以看出：当L=400 mm时，颗粒未在沉降室发生沉降，直接从出风管逃逸而出；当L=600 mm时，部分颗粒与固定阀板发生弹性碰撞后发生沉降，但是在灰斗左侧存在高速涡流区，不利于颗粒向出风口提升，部分颗粒将再次沉降，沉降能力增大；当L=800 mm时，在升降阀板导流作用下颗粒运动角度增大，大量颗粒在灰斗与固定阀板之间来回碰撞后沉降；L=1 000 mm时，大量颗粒沿着固定阀板向下运动，运动至固定阀板末端时部分颗粒被气流二次吹起，从固定阀板右侧经右转动阀板从出风管逃逸而出。

2.3 升降阀板对沉降室沉降性能的影响

为了更加精确地研究沉降室沉降效果，根据风选箱进料级配，从风选箱进料口喷射5组Rosin-Rammler分布的颗粒源，每组喷射7 080个颗粒，然后统计颗粒数目。表2和表3分别为沉降室沉降口、出风口颗粒分布。图6和图7分别为相应的沉降室沉降效率和选粉效率变化曲线。

从图中可以看出，当L=600 mm，800 mm，1 000 mm时，颗粒沉降效率大，L=400 mm时，沉降能力较弱。随着颗粒粒径的增大，沉降效率呈现出先增大后减小的趋势，其中，当L=600 mm、颗粒粒径为75～150μm时，沉降效率最大为68.23%；但是随着颗粒粒径的增大，出风口处的颗粒数目逐渐减少，这就意味着在颗粒总数目一定的条件下，在风选箱物料出口被收集的颗粒数目逐渐增多，这是因为升降阀板长度增大时，沉降室设备的阻力将会增大，从而导致风选箱对颗粒的吸附能力减弱。

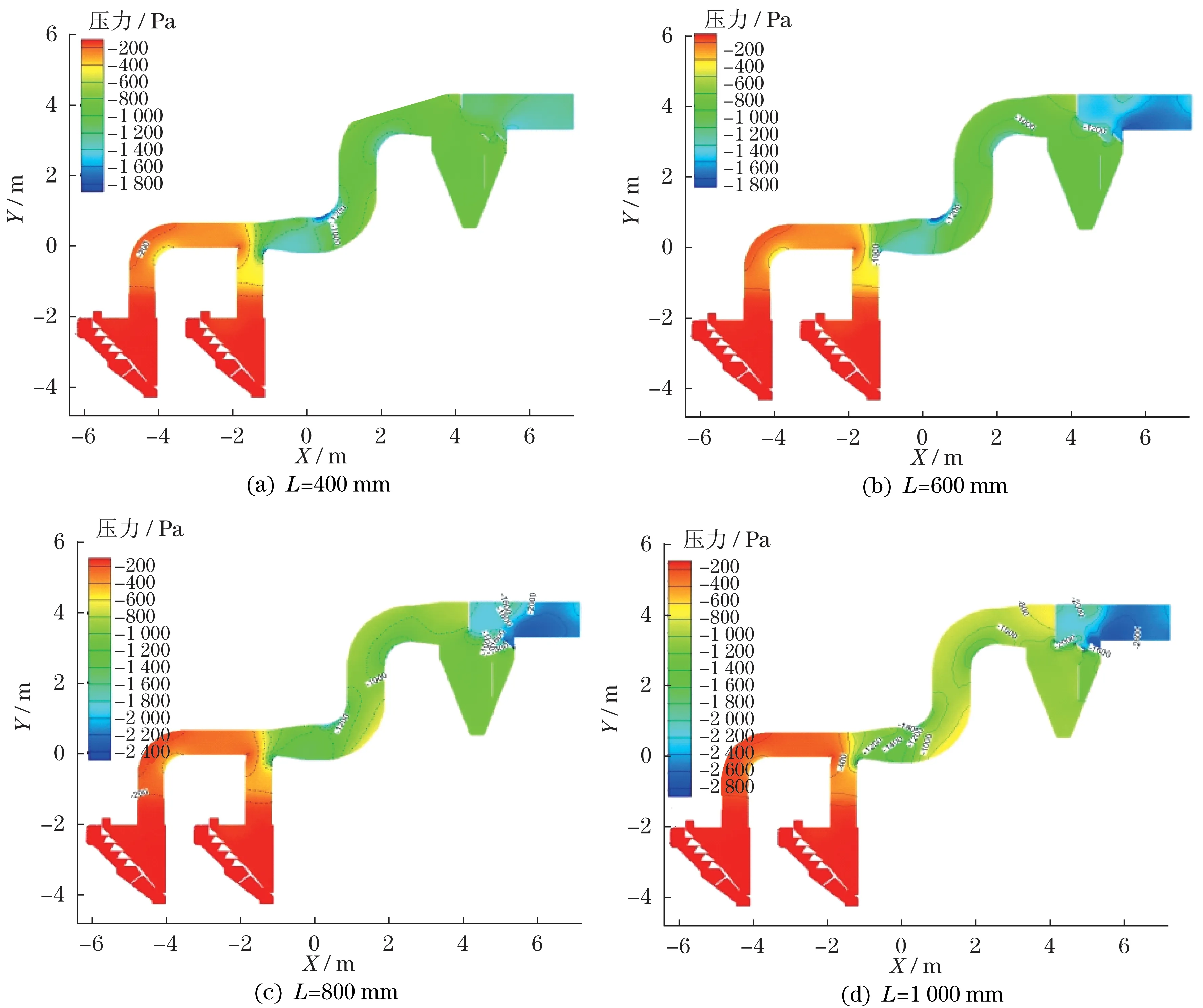
图4 不同升降阀板长度下沉降系统的压力云图Fig.4 The pressure cloud map under different lifting valve plate lengths

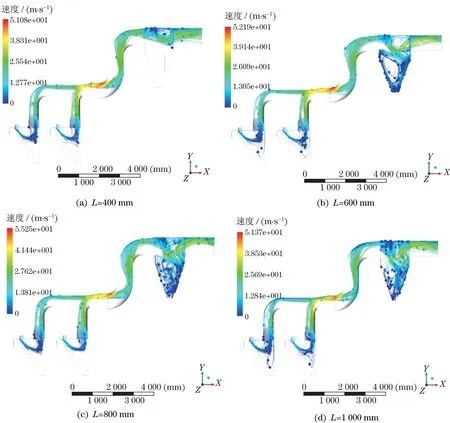
图5 不同升降阀板长度下粒径45～75μm颗粒运动轨迹Fig.5 The moving locus of the 45～75μm size particle under different lifting valve plate lengths

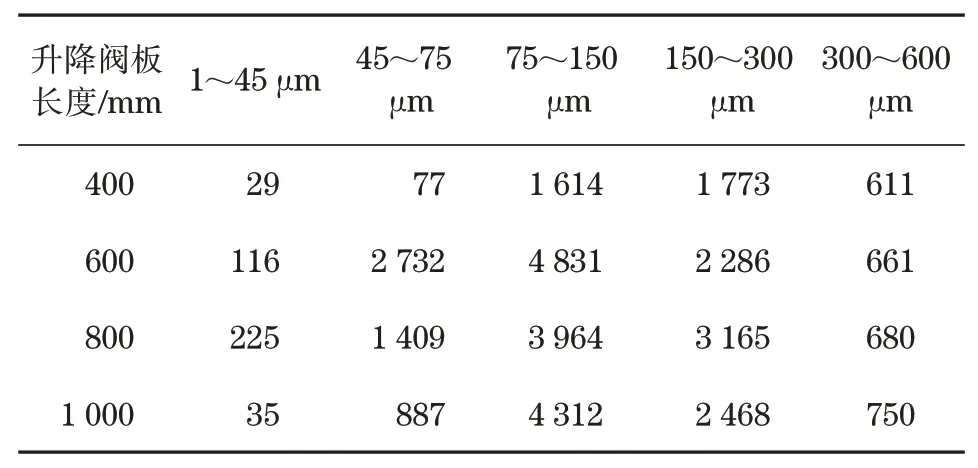
表2 沉降室沉降口颗粒分布Tab.2 The inlet particle distribution of the settlement chamber

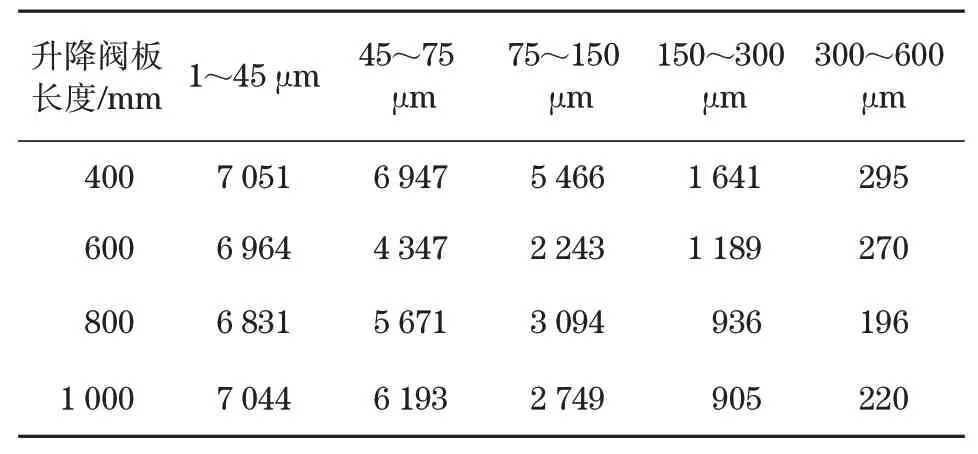
表3 沉降室出风口颗粒分布Tab.3 The air outlet particle distribution of the settlement chamber

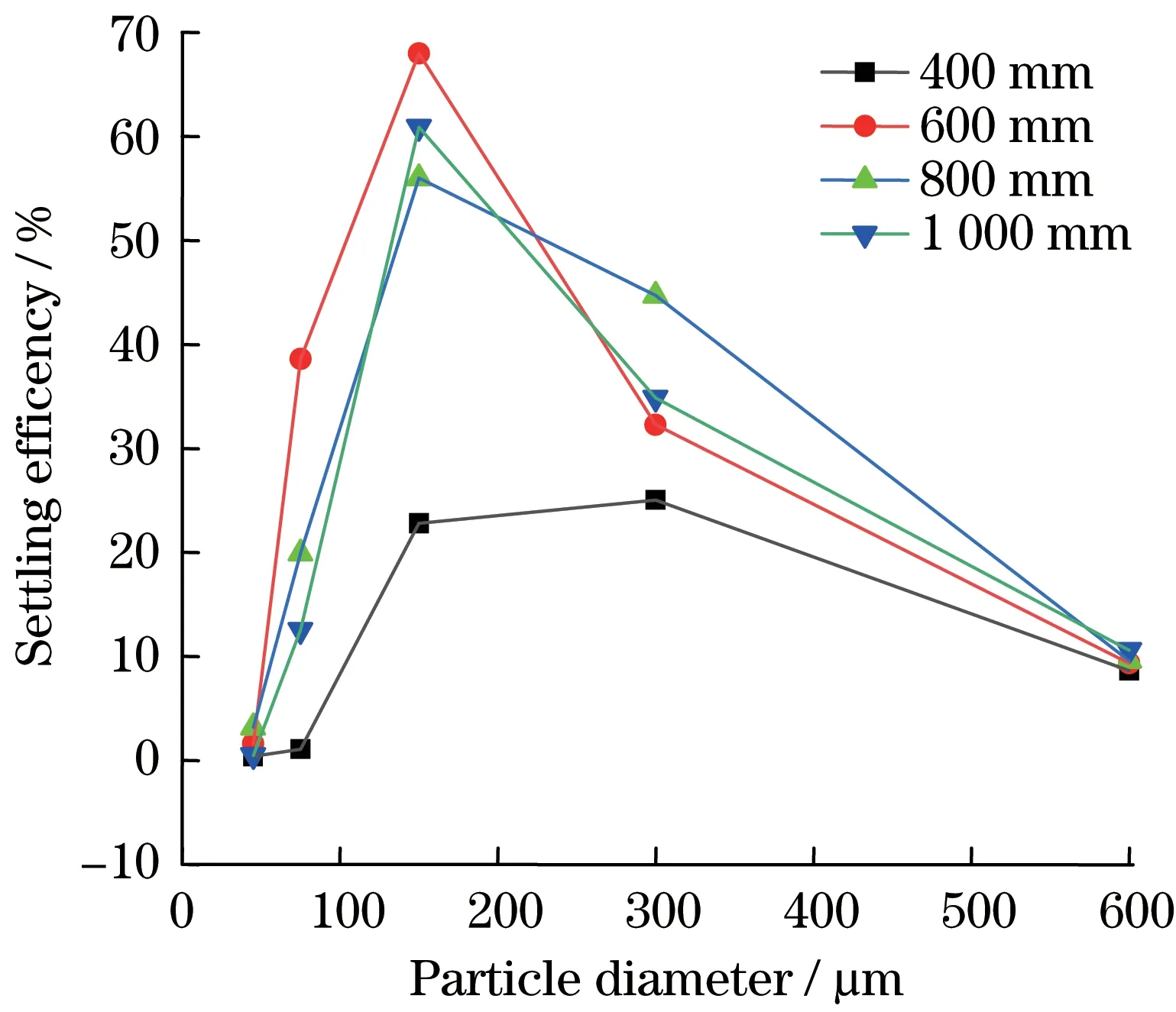
图6 不同升降阀板长度下沉降室沉降效率Fig.6 Sedimentation efficiency under different lifting valve plate lengths

2.4 升降阀板对沉降室设备阻力的影响

图8 为不同升降阀板长度下沉降系统阻力的变化曲线。由图可见，随着升降阀板长度的增加，升降阀板与右转动阀板间的过流面积减小，沉降室、风管的阻力都明显增大。

2.5 气流对升降阀板的影响

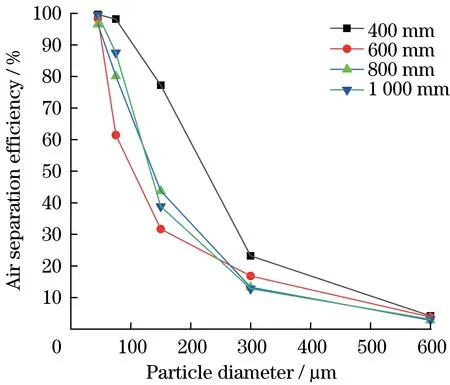
图7 不同升降阀板长度下沉降室选粉效率Fig.7 Separating efficiency under different lifting valve plate lengths

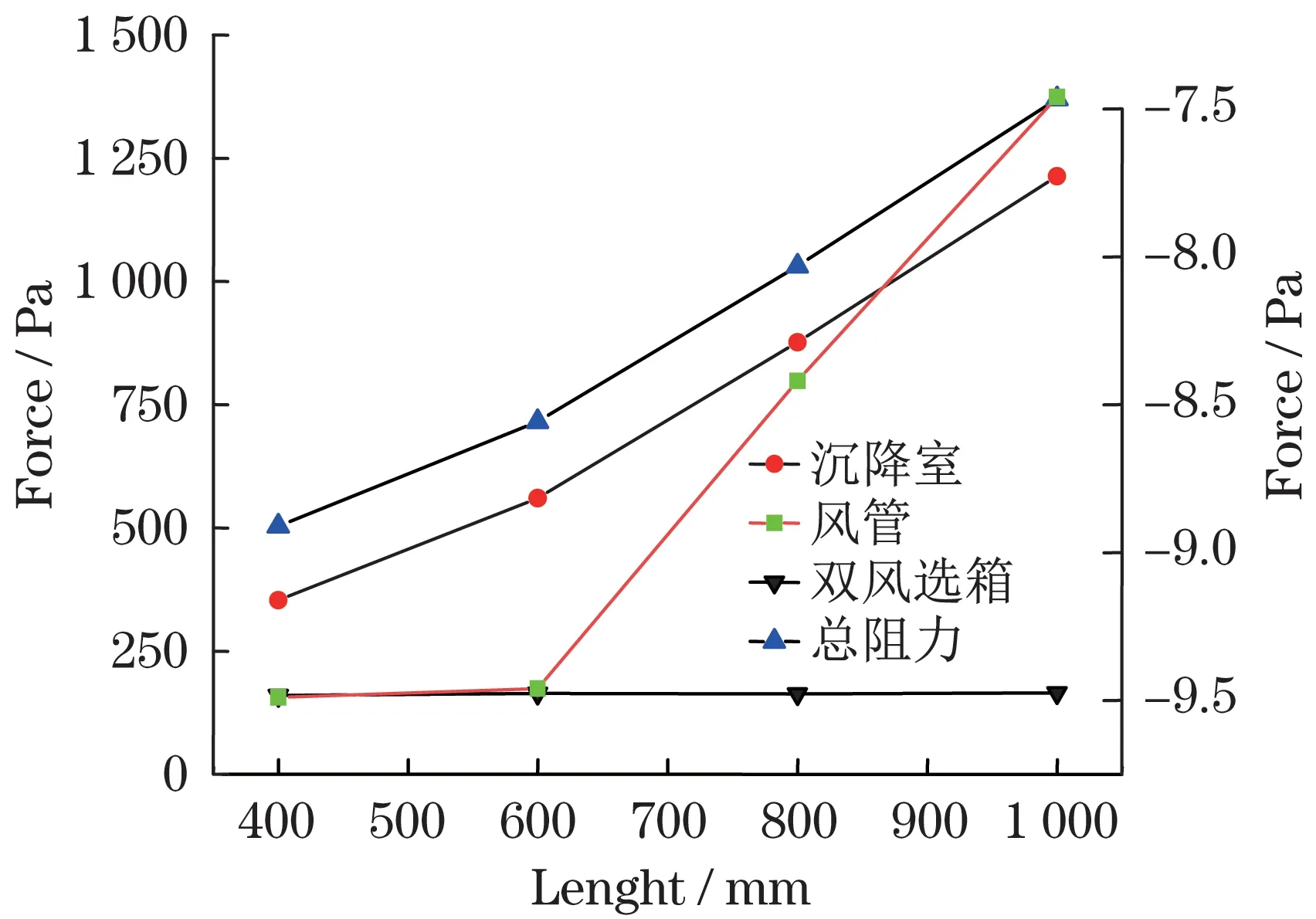
图8 不同升降阀板长度下沉降系统阻力Fig.8 Resistance of settlement system under different lifting valve plate lengths

当升降阀板的长度为1 000 mm时，采用流固耦合的方法计算气流对升降阀板的作用效果。图9和图10分别为计算得到的沉降室应力、应变云图。由图可见：升降阀板与壁面连接处的应力最大，达到19.13 MPa；升降阀板下端处的应力在未连接区域最大，达到7.19 MPa，皆满足沉降室使用的强度要求。在升降阀板的下端和沉降室前后侧板的应变最大，达到0.73 mm，满足沉降室的刚度要求。

图9 沉降室应力云图Fig.9 Stress cloud of the settlement chamber

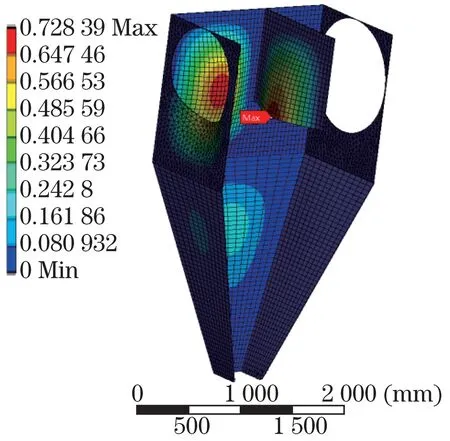
图10 沉降室应变云图Fig.10 Strain cloud of the settlement chamber

3 结论

本文采用Realizablek-ε湍流模型和Euler-Lagrange离散相模型，研究了升降阀板长度对沉降室的影响，进行了气固两相流场和流固耦合数值计算，发现沉降室升降阀板的长度对砂石颗粒的气力分级具有显著的影响，具体结论如下：

（1）随着升降阀板长度L的增加，沉降室内气流速度大小发生分级，气流方向在升降阀板位置发生重大改变，使砂石颗粒从气流中分离出来，发生沉降；同时压阻增大，在升降阀板左右两侧产生明显的压力分界线。

（2）在升降阀板长度L=600 mm时，沉降效率最高，粒径75～150μm颗粒沉降效率为68.23%，选粉率最低，最符合砂石级配和实际工况要求。

（3）升降阀板和沉降室的最大应力为19.13 MPa，最大应变为0.73 mm，满足设备使用的强度和刚度要求。