基于复合控制的电液执行机构驱动阀门跟踪误差研究

杨小庆，赵振华

（1.重庆工商职业学院智能制造与汽车学院，重庆400052；2.武汉工程大学电气信息学院，湖北武汉430073）

传统的发动机气门阀大多采用机械式凸轮轴驱动，通过凸轮轴实现气门的开启和关闭。这种机械式驱动机构相对简单，而且费用较低。但是，气门阀在开启时，气门升程运动参数往往是固定不变的，不能根据工况进行在线调节，导致气门阀着陆时振动幅度较大，具有一定的局限性。无凸轮可变配气机构能够根据发动机工况的不同，对气门的开启和关闭时刻进行调整，从而改善气门阀工作性能，在发动机配气机构中应用也越来越普遍。电液驱动可变配气机构是无凸轮可变配气机构中的一种，通过压缩性较小的弹性特征对气门运动进行加速和减速，为气门阀运动提供了连续可变控制［1-2］。但是，随着社会智能化技术的不断发展，人们对发动机产生的噪声要求越来越小，电液驱动可变配气机构必须增加更好的控制方法，才能更好地满足人们的需求。因此，研究电液可变配气机构控制方法，对于提高气门阀运动精度和稳定性具有重要的意义。

为了提高气门阀升程运动轨迹跟踪精度，降低气门阀落座的振动幅度，许多科研工作者从不同角度对气门阀运动轨迹展开了研究。例如：文献［3-4］研究了可变液压气门机构的气门落座特性，建立了气门驱动机构和落座缓冲机构示意图，分析了气门控制机构的工作原理，通过实验比较不同速度下气门落座时的升程和速度，为气门平稳落座提供了参考数据。文献［5-6］研究了液压可变气门运动控制方法，分析了气门运动特性，分别从气门相位、气门升程及不同转速下气门的稳定性方面进行控制，为进一步完善液压可变气门技术奠定了基础。文献［7-8］研究了发动机配气机构气门阀运动特性，搭建了气门运动的实验平台，研究了发动机不同转速下的能量消耗和气门开启时间，改善了发动机动力性和经济性。气门阀升程运动以往采用的控制方法，运动位移和速度跟踪误差较大，导致气门阀着陆时振动幅度较大，噪声较大。对此，本文建立了气门阀液压驱动系统平面简图，引用高斯函数设计气门阀运动轨迹，推导出液压驱动系统压力和流量变化方程式，采用前馈控制和二次线性组合控制方法，利用Matlab软件对气门升程运动位移和速度跟踪误差进行仿真，并且与前馈控制方法输出效果形成对比，为深入研究气门阀升程运动位移和速度提供参考数据。

1 液压驱动系统

本文研究的是发动机气门阀液压执行机构，如图1所示。

图1 发动机气门阀液压驱动系统Fig.1 Engine valve hydraulic drive syste

图中，P0为液压动力源提供的绝对压力，PT为液压油箱的压力，PA（t）为液压缸腔室A中的压力，PB（t）为液压缸腔室B中的压力，x2（t）为伺服阀阀芯的位置。液压执行机构工作原理如下：当x2（t）＞0时，液压油从P0端口进入，从PA（t）端口流出，然后从PB（t）端口流入，从PT流出，气门逐渐打开。当x2（t）=0时，液压油处于静止状态，气门处于最大开度状态。当x2（t）＜0时，液压油从P0端口进入，从PB（t）端口流出，然后从PA（t）端口流入，从PT流出，气门逐渐关闭。

发动机气门轨迹运动曲线选择高斯函数［9］：

式中：L为最大气门升程；m为斜率因子；b为孔直径；a和c为常数；t为时间。

通过线性二阶常微分方程描述发动机气门的运动方程为

式中：Mv为液压活塞和发动机气门质量；bv为阻尼系数；S为气缸活塞面积；Δp（t）为压力差；d（t）为不确定影响因素。

假设液压流体是可压缩的，则用于气缸室中的压力动态的微分方程［10］为

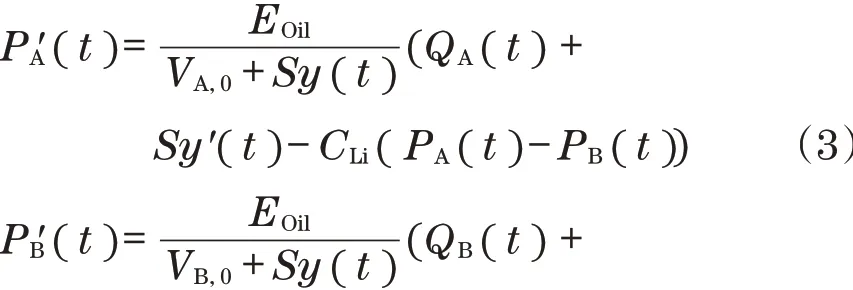
式中：VA，0、VB，0分别为A缸和B缸的初始体积；EOil为油的体积模量；QA（t）、QB（t）分别为A缸和B缸的流量；CLi为泄露系数。

可以通过阀门阀芯位置调节进出液压腔室的体积流量QA（t）和QB（t）。它允许在x2（t）=0时的情况下关闭的流量，即阀芯的中间位置。关于体积流量的简明符号描述，定义如下函数sg（x）：

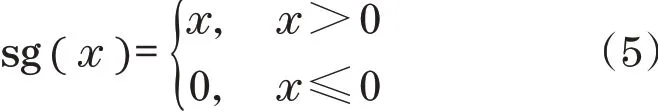
流量方程定义为

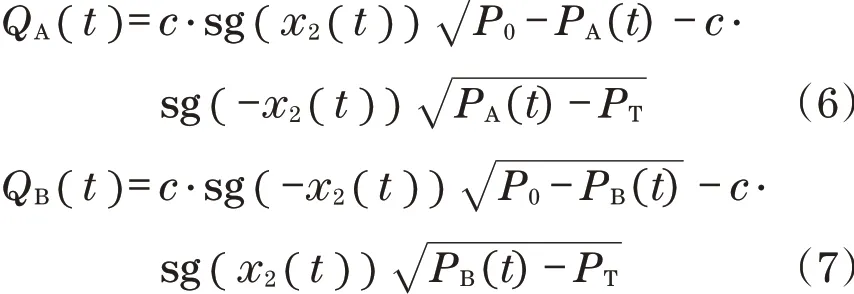
式中：c为水力系数。

液压系统部件的非线性状态空间表示为

其中，

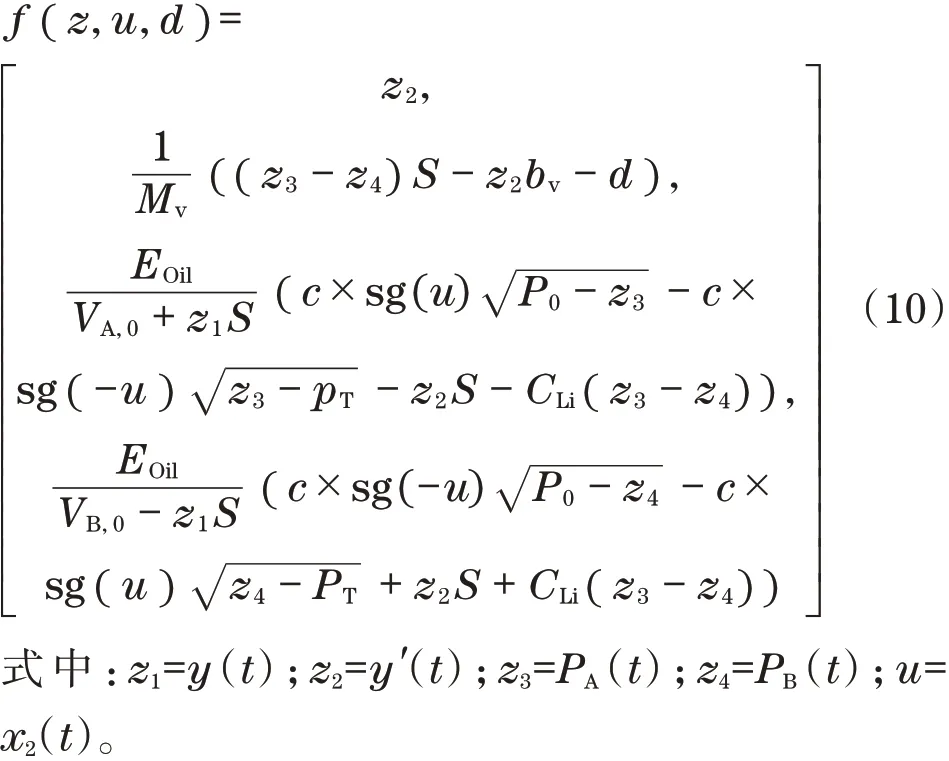
2 复合控制器设计

2.1 前馈控制

考虑压电驱动阀芯的前馈控制设计，给定阀芯位置的期望轨迹，确定用于对抗压电元件的必要输入信号。为了减少实施工作量，减少不必要的模型是合理的。因此，采用以下二阶系统用于前馈控制［11-12］设计：

式中：Vz1（t）、Vz2（t）为输入电压；AD2、BD2和CD2为矩阵。

前馈控制策略采用对称输入电压为

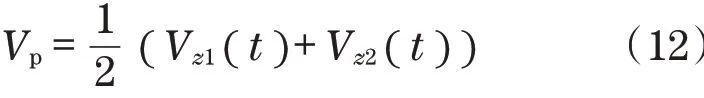
为了获得可逆的前馈控制系统模型，引入Vp作为附加状态。此外，BD2矩阵被划分为如下两列：

对前馈控制系统模型进行扩展，可以表示为

式中：

前馈控制系统模型的传递函数为

式中：a1、a2、a3、b1为常数。

2.2 线性二次控制

采用输入-输出线性化来控制非线性系统，必须使用合适的线性控制策略，才能在最终设计步骤中稳定该线性系统。如果表征输入-输出动态顺序的相对度小于系统顺序，则存在内部动态。输入-输出线性化可实现性的条件是内部动态的稳定性，这是整个系统动态不可观察的部分。通常，通过仅考虑零动态来简化稳定性分析。液压执行器驱动力变化输出定义为

式中：

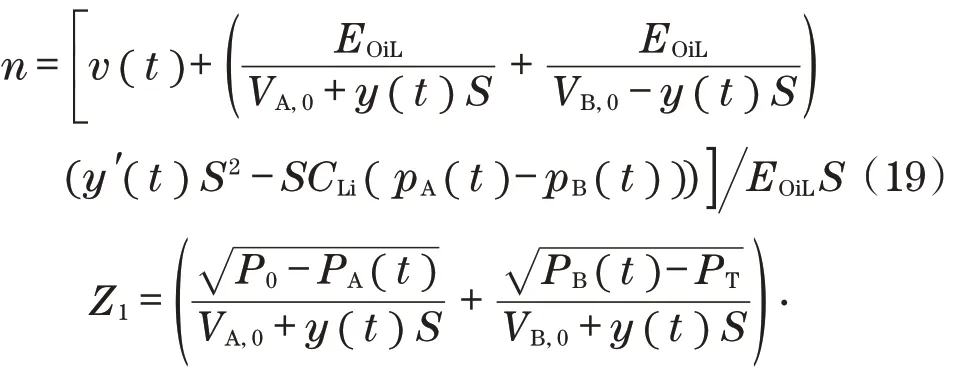
为了避免代数循环，利用Heaviside函数H，根据sg（x2d（t））=x2d（t）H（x2d（t-T）），将x2d（t）在等式右边延迟一个采样时间步长T。除稳定输入v（t）外，所有其他信号都可以从估计中得到，并用于逆动力学。采用估计值而不是噪声测量通常会得到更好的结果，因为噪声特性可以被充分利用，例如通过卡尔曼滤波方法，卡尔曼滤波器还可以利用系统的先验知识，以系统模型方程的形式对不可测量状态进行估计。在给定的情况下，发动机气门位置是用于反馈的唯一可测量信号，而其余的则通过级联扩展卡尔曼滤波器结构估计。

选择稳定控制律v（t）作为线性二次最优控制，由发动机气门位置和状态跟踪误差的比例积分反馈组成。状态空间表示为

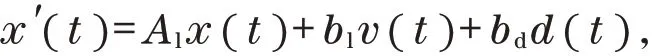
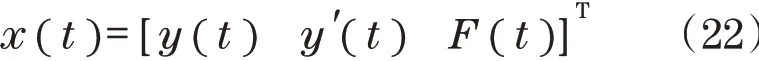
式中：

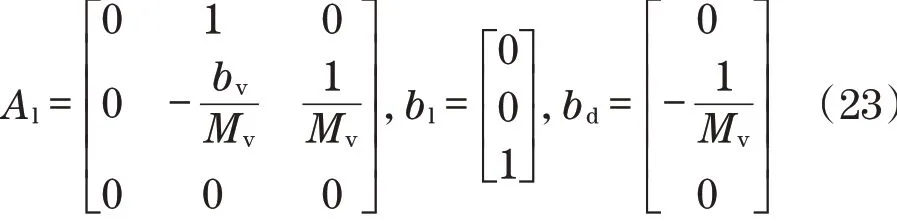
选取状态变量x（t）和控制变量v（t）的二次型函数的积分控制指标：

式中：Q为跟踪误差加权矩阵；R为控制信号加权矩阵。

2.3 级联扩展卡尔曼滤波器结构

本文采用级联扩展卡尔曼滤波器结构［13-14］，组合控制器结构如图2所示，其状态空间描述如下：

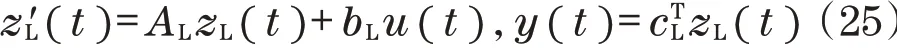
式中：

图2 组合控制器Fig.2 Combined controller

这里忽略扰动力d（t）。采用显式欧拉方法的时间离散化，即Ad，L=I2×2+ALTs，bd，L=bLTs，允许对状态进行先验估计：

式中：

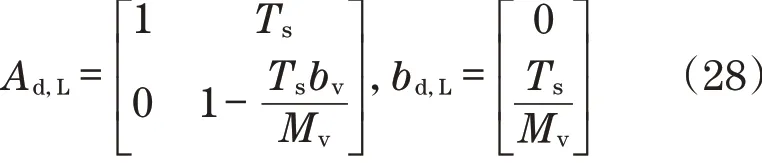
此外，估计误差的协方差矩阵可以预先估计：

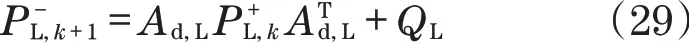
卡尔曼增益可以简化为

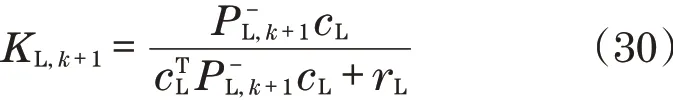
一旦新的测量值ym可用，就可以对状态和估计误差的协方差进行后验估计：

3 仿真及分析

为了比较前馈控制和复合控制气门阀跟踪效果，采用Matlab软件对气门运动位移和运动速度跟踪效果进行仿真。仿真参数设置如下：气门最大升程为L=10 mm，发动机转速为ne=2 000 r/min，阻尼系数为bv=0.1 kg/s，气缸活塞面积为S=0.75 cm2。采用前馈控制和复合控制的气门阀位移跟踪结果分别如图3和图4所示，采用前馈控制和复合控制的气门阀速度跟踪结果分别如图5和图6所示。

图3 气门阀位移跟踪结果（前馈控制）Fig.3 Valve displacement tracking results（feedforward control）

图4 气门阀位移跟踪结果（复合控制）Fig.4 Valve displacement tracking results（compound control）

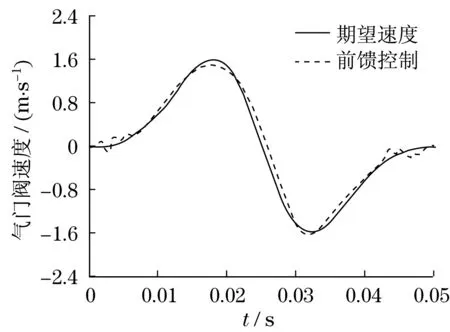
图5 气门阀速度跟踪结果（前馈控制）Fig.5 Valve speed tracking results（feedforward control）

根据图3可知，采用前馈控制方法，在升程初始阶段和回程结束阶段内，气门阀位移跟踪误差较大。根据图4可知，采用复合控制方法，在升程初始阶段和回程结束阶段内，气门阀位移跟踪误差较小。根据图5可知，采用前馈控制方法，在升程初始阶段和回程结束阶段内，气门阀速度跟踪误差较大。根据图6可知，采用复合控制方法，在升程初始阶段和回程结束阶段内，气门阀速度跟踪误差较小。因此，采用复合控制方法，气门阀位移和速度跟踪误差较小，可以精确跟踪所需的气门轨迹，特别是在回程阶段，能够实现气门阀软着陆，运动相对稳定。

图6 气门阀速度跟踪结果（复合控制）Fig.6 Valve speed tracking results（compound control）

4 结论

针对气门阀升程运动位移跟踪误差较大、导致气门阀着陆不稳定问题，设计了气门阀复合控制方法，通过仿真评估气门阀升程位移和速度跟踪误差结果，主要结论如下：

（1）采用电液伺服阀驱动气门阀运动，建立气门阀压力和流量方程式，引用高斯函数设计气门阀运动轨迹，使气门阀升程运动相对稳定。

（2）根据输入-输出线性化，采用前馈控制和二次线性控制进行组合，通过级联扩展卡尔曼滤波器，气门阀升程运动位移和速度跟踪误差较小，从而实现气门阀软着陆。

（3）本文只研究了气门阀升程位移和速度跟踪误差，对于气门阀落地受到冲击力大小变化没有研究，未来可以作为一个研究方向。