低剪跨比内嵌钢板−混凝土组合剪力墙抗剪性能试验研究

张世江，郭子雄,2，刘阳,2，武豪

(1.华侨大学土木工程学院，福建厦门，361021；2.华侨大学福建省结构工程与防灾重点实验室，福建厦门，361021)

内嵌钢板−混凝土组合剪力墙作为一种新型的钢−混凝土组合结构体系，具有较大的抗侧刚度、较强的变形能力和抗震性能等[1−3]，已作为一种有效抗侧力构件应用于高层和超高层建筑结构中[4−5]。近年来，为充分发挥内嵌钢板−混凝土组合剪力墙的力学性能，郭兰慧等[6−12]完成了两边连接钢板组合剪力墙、钢连梁−内嵌钢板混凝土组合剪力墙、方钢管混凝土暗柱内嵌钢板−混凝土组合剪力墙、钢管混凝土边柱−内嵌多重钢板剪力墙、波纹钢板剪力墙和开洞钢板剪力墙的拟静力试验，但所研究的内容主要集中在各种构造措施对内嵌钢板−混凝土组合剪力墙抗震性能的影响，对其抗剪性能的分析较少。对内嵌钢板−混凝土组合剪力墙抗剪性能的研究主要有：孙建超等[13]进行了11 个高宽比为1.5的内嵌钢板−混凝土组合剪力墙抗剪试验，并基于承载力叠加原理提出了钢板混凝土剪力墙的受剪承载力计算公式。吕西林等[14]通过拟静力试验研究了高宽比、墙体厚度和钢板厚度等参数对内嵌钢板−混凝土组合剪力墙抗震性能的影响，并基于试验数据拟合了组合剪力墙的受剪承载力计算公式。纪晓东等[15]通过拟静力试验对比了内嵌钢板和外包钢板混凝土墙的抗剪性能，通过分析国内外46 个钢板混凝土墙试验数据，发现按规程JGJ 3—2010 的计算公式所得钢板混凝土墙的受剪承载力平均为试验值的78%。SHAFAEI 等[16]采用有限元分析了钢筋混凝土板和钢板厚度对内嵌钢板−混凝土组合剪力墙抗剪性能的影响。WANG等[17]通过拟静力试验研究了钢筋混凝土剪力墙和内嵌钢板混凝土剪力墙的抗震性能，并基于规范JGJ 138—2016修正了内嵌钢板−混凝土组合剪力墙受剪承载力计算公式。BOOTH 等[18]采用非线性非弹性有限元模型和理论解析的方法提出了带边缘构件的钢板剪力墙平面内极限抗剪承载力计算方法。然而，目前对内嵌钢板−混凝土组合剪力墙抗剪性能的研究仍不充分，已有试验均施加较大的轴压力，试件的破坏形态多为墙底部的压弯破坏，纯剪试验较少，不能完全反映墙体剪切破坏性能，且现行规范并未考虑剪跨比对剪跨比λ≤1.5的组合剪力墙抗剪性能的影响。为此，本文作者通过6个低剪跨比内嵌钢板−混凝土组合剪力墙单点加载的抗剪试验，研究钢板厚度和剪跨比对低剪跨比内嵌钢板−混凝土组合剪力墙受剪性能的影响。

1 试验概况

1.1 试件设计

设计并制作了6 个内嵌钢板−混凝土组合剪力墙试件(试件SW-1～SW-6)，研究参数为钢板厚度和剪跨比λ(λ=a/h，a为加载点到支承点的距离，h为墙截面高度)。试件采用缩尺模型，墙截面尺寸根据加载装置的能力确定。图1所示为试件结构示意图，由图1可见：为简化试验装置，剪力墙试件由2 片相同墙体拼接并翻转90°的方向放置。剪力墙试件采用工字型钢代表边缘构件，通过增大试件下部工字型钢截面尺寸提高其抗弯性能，从而使试件发生剪切破坏，以研究剪力墙的抗剪性能；试件上部设置工字型钢代表翼墙，工字钢截面高×宽×腹板宽×翼缘厚为100 mm×100 mm×20 mm×20 mm；试件竖向设置十字型钢代表框架梁，工字钢截面高×宽×腹板宽×翼缘厚为200 mm×200 mm×20 mm×20 mm，中部框架梁为加载梁，通过配置4根20 钢筋并筑混凝土，以保证其在加载过程中不被破坏。试件编号及主要参数如表1所示。

图1 内嵌钢板−混凝土组合剪力墙示意图Fig.1 Schematic diagram of steel plate reinforced concrete shear wall

表1 试件主要参数Table 1 Main parameters of specimens

图2所示为典型试件SW-1和SW-2的截面尺寸和细部构造。由图2可见：各试件墙截面高×宽均为800 mm×100 mm，试件SW-1～SW-2，SW-3～SW-4和SW-5～SW-6 加载点到支承点的距离分别为600，800和1 000 mm，剪跨比分别为0.75，1.00和1.25。每一级剪跨比下设置钢板厚度为4 mm和8 mm的2个试件，钢板表面焊接直径为8 mm、长度为35 mm的栓钉，间距100 mm。腹板墙的水平和竖向分布钢筋直径为8 mm、长度为100 mm，采用焊接方式与型钢边缘构件连接。各试件混凝土的设计强度等级均为C30(实测立方体抗压强度标准值fcu,k=30.5 MPa，轴心抗拉强度通过实测立方体抗压强度实测值换算得到[19])。试验中所用钢板和型钢均为Q235 钢材，钢筋为HPB300 级钢筋，钢材和钢筋的性能见表2。

图2 SW-1和SW-2截面尺寸及细部构造Fig.2 Dimensions of cross section and details of SW-1and SW-2

表2 钢材性能Table 2 Material properties of steel

1.2 试验加载与量测

图3所示为试验加载装置图。由图3可见：刚性反力架位置固定，通过刚性加载台座对试件施加荷载，剪跨比为0.75，1.00和1.25的试件型钢混凝土加载梁截面形心与支座的距离分别为600，800 和1 000 mm。试件两端铰支，左端为滑动铰支座，右端为固定铰支座。

图3 试验加载装置Fig.3 Test loading setup

加载过程采用力−位移混合控制方法，即试件在弹性阶段按照力控制分级加载，在预测的峰值荷载之前，各加载级的目标荷载分别为预测峰值荷载的10%，20%，…，70%，80%，为检测试件的损伤程度，每级加载到目标荷载后先卸载为0，再进行下一级加载；当试件加载端荷载−位移曲线出现明显转折时即认为试件屈服，屈服后采用位移控制单向加载，直至试件被破坏。

试件位移计及应变片布置如图4所示。在试件整体跨中以及单片墙体跨中位置设位移计D1～D3，量测试件的竖向位移；在单片墙体对角线分别设置1 对交叉位移计(D4～D5，D6～D7)量测墙体的剪切变形；在内嵌钢板上设置5 个应变花(B1～B5)，量测钢板的应变；在水平分布钢筋上设置4个应变片(P1～P4)，量测水平分布钢筋的应变；在竖向分布钢筋上设置3 个应变片(Z1～Z3)，量测竖向分布钢筋的应变。

图4 位移计以及应变片布置Fig.4 Layout details of displacement meter and strain gauges

2 试验结果及分析

2.1 试验过程及破坏特征

加载结束时各试件均在固定铰支座一侧的墙体发生剪切破坏，最终破坏形态如图5所示，以试件SW-1为例描述破坏过程。

从图5可见：开裂荷载前，各试件荷载−位移曲线基本呈线性变化，无明显试验现象；当试件SW-1 的荷载达到900 kN(相应为峰值荷载的31%)时，左侧墙体混凝土开始出现沿斜压杆带方向的剪切斜裂缝，此时，试件的竖向位移为1.48 mm，卸载后的残余变形为0.46 mm。随着荷载的增大，试件墙体已有斜裂缝发展，裂缝变宽，两侧墙体均出现剪切斜裂缝；当荷载达到1 800 kN 时，荷载−位移曲线开始出现一定程度的转折，钢板、分布钢筋的应变达到屈服应变；当试件SW-1的荷载达到2 700 kN(相应为峰值荷载的93%)时，右侧墙体混凝土裂缝迅速发展，已有斜裂缝逐渐延伸至试件端部，形成多条贯通裂缝，同时，水平分布钢筋位置混凝土出现水平裂缝，此时，试件的竖向位移为4.66 mm，卸载后的残余变形为2.75 mm；当荷载增大到峰值荷载2 917 kN时，右侧墙体混凝土严重剥落，水平分布钢筋压屈、外鼓，最终，右侧墙体混凝土形成斜压杆裂缝带，而左侧墙体混凝土开裂后仅产生少量剥落并没有达到极限破坏的效果，这可能是由于右侧为固定铰支座，导致加载位置偏离。加载过程中未出现剪力墙的侧向失稳，墙体的最终破坏形态主要为斜向剪切破坏。

2.2 荷载−位移曲线和骨架曲线

图6所示为各试件的荷载V−位移Δ曲线。由图6可见钢板剪力墙试件的受力过程主要呈3 阶段发展：1)弹性阶段，在加载初期，各试件的荷载−位移曲线基本呈线性关系，卸载后残余变形较小，在重复加载过程中，试件刚度几乎没有退化，基本处于弹性工作状态；2)弹塑性阶段，随着荷载增大，混凝土开裂，试件刚度下降，卸载后残余变形逐渐增大，钢板和分布钢筋的应变达到屈服应变；3)破坏阶段，在峰值荷载后，试件的承载力下降较平缓，表现出较好的延性，主要原因是混凝土裂缝迅速发展，逐渐压碎、剥落而退出工作，荷载主要由型钢边缘构件和钢板组成的抗剪体系承担。

图5 试件破坏形态Fig.5 Failure modes of specimens

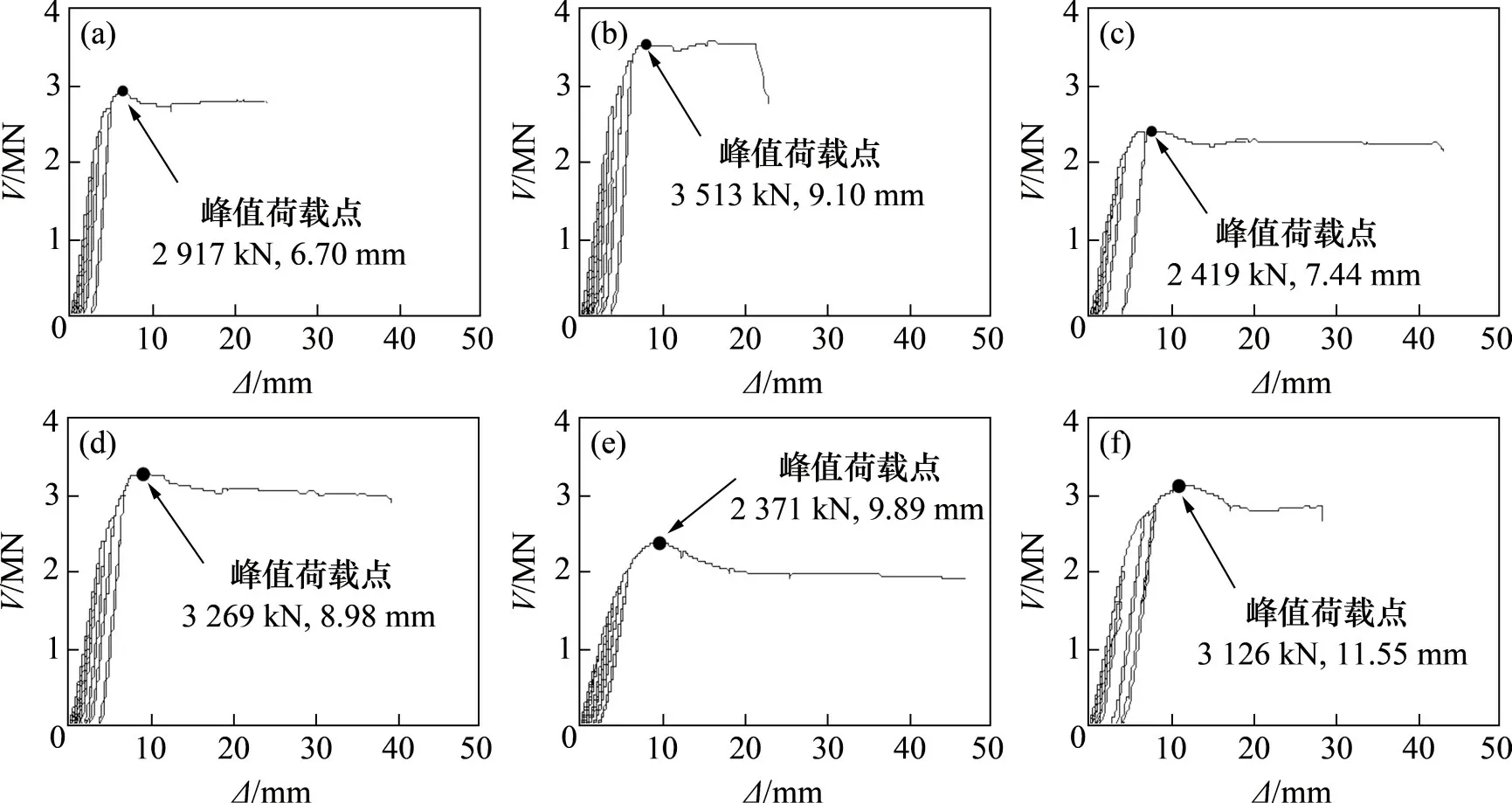
图6 试件荷载−位移曲线Fig.6 Load−displacement curves of specimens

图7所示为各试件的荷载−位移骨架曲线。由图7可见：各试件的初始刚度基本一致；当荷载超过屈服荷载时，钢板厚度较大的试件表现出比钢板厚度较小的试件更大的刚度和承载力，整体变形能力略有降低；当剪跨比增大时，试件的刚度和承载力逐渐降低，变形能力显著提高。

图7 试件荷载−位移骨架曲线Fig.7 Skeleton curves of load−displacement of specimens

2.3 荷载−墙体剪切变形角骨架曲线

各试件荷载−墙体剪切变形角γ骨架曲线如图8所示，墙体剪切变形由交叉位移计6和7量测的数据计算得到。由图8可见：在整个加载过程中，各试件墙体剪切变形的发展规律与位移的变化规律相似。各试件的极限剪切变形角相近，表明钢板厚度和剪跨比对墙体剪切变形能力的影响较小。

2.4 承载力

各试件名义屈服荷载和峰值荷载见表3。试件的名义屈服点用能量等值法[20]确定，各试件名义屈服荷载约为峰值荷载的93%。由表3可见：当内置钢板的厚度从4 mm 提高至8 mm 时，试件SW-2，SW-4和SW-6的峰值荷载分别比试件SW-1，SW-3，SW-5 的峰值荷载提高20.4%，35.1%和31.8%，表明内置钢板厚度的增大可以显著提高试件的受剪承载力。然而，当增大剪跨比时，试件SW-3 和SW-5 的峰值荷载分别比试件SW-1 的峰值荷载小17.1%和18.7%；试件SW-4 和SW-6 的峰值荷载分别比试件SW-2 的峰值荷载小6.9%和11.0%，表明随着构件剪跨比的增大，试件的受剪承载力逐渐减小，且钢板厚度较小的试件受剪承载力下降幅度更大，剪跨比对钢板厚度较小的试件的受剪承载力影响更大。

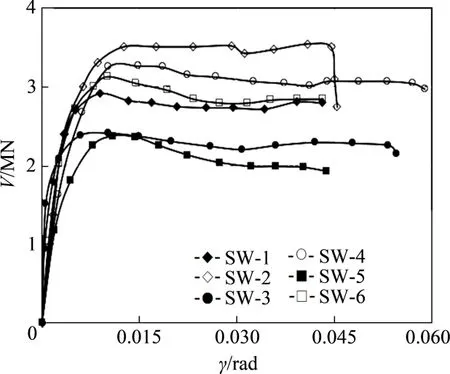
图8 试件剪力−剪切变形角骨架曲线Fig.8 Skeleton curves of shear force−displacement of specimens

2.5 变形

各试件的名义屈服位移Δy、屈服荷载Vy、峰值荷载Vm及其对应的位移Δm、极限荷载Δu及其对应的位移Δu、极限位移Δu和极限位移角θu(θu=Δu/a)见表3。其中，名义屈服位移Δy为名义屈服点对应的位移，由于部分试件承载力未下降至0.85Vm，因此，Vu和Δu均为荷载下降至0.95Vm时的荷载和对应的位移。由表3可知：各试件均具有良好的变形能力；试件SW-2，SW-4 和SW-6 的极限位移角与试件SW-1，SW-3 和SW-5 的极限位移角相差不大，表明钢板厚度对试件的变形能力影响较小；试件SW-3 和SW-5 的极限位移角分别比试件SW-1 的极限位移角小64.7%和67.9%；试件SW-4 和SW-6 的极限位移角分别比试件SW-2 的极限位移角小49.6%和56.5%，表明随着构件剪跨比的增大，试件的变形能力逐渐减小，剪跨比对钢板厚度较小的试件的变形能力影响更大。

2.6 损伤

图9所示为各试件在各级荷载卸载到零时的残余变形Δr−位移角曲线。由图9可见：在加载过程中，各试件的残余变形持续、稳定增大；加载初期，各试件的残余变形相差较小；位移角达到0.4%之后，各试件残余变形迅速增大；在相同位移角下，试件SW-1 和SW-2 表现出比试件SW-3～SW-6 更小的残余变形，表明较小剪跨比试件的残余变形更小，损伤较小；试件SW-2，SW-4 和SW-6的残余变形分别与试件SW-1，SW-3和SW-5的残余变形相近，表明钢板厚度对试件的残余变形没有明显的影响。

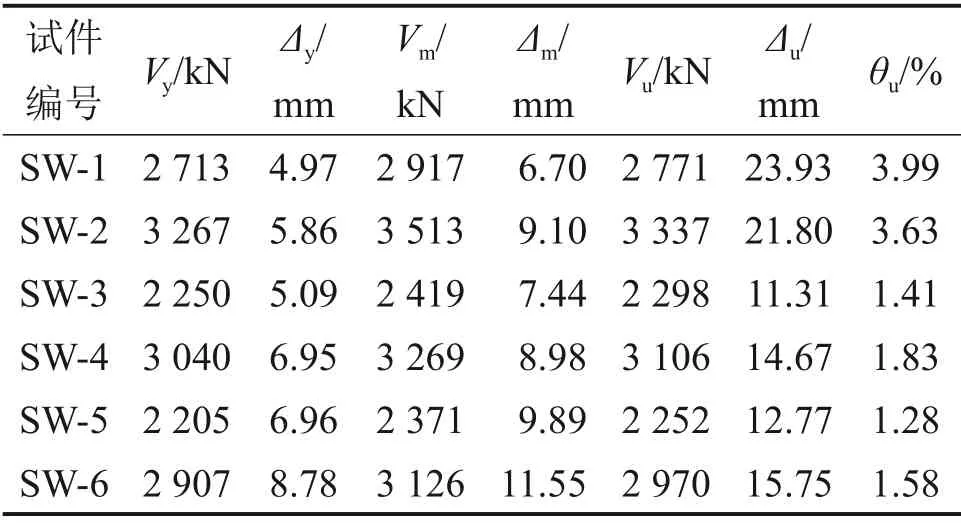
表3 骨架曲线主要特征点试验结果Table 3 Test results of characteristic points of skeleton curves

2.7 应变

图10和图11所示分别为钢板和水平分布钢筋的荷载−应变曲线，钢板的主应变由应变花实测数据计算得到。由图10和图11可见：在加载初期，钢板和水平分布钢筋的应变较小；到达屈服荷载时，钢板应变迅速增大；到峰值荷载时，钢板已屈服，水平分布钢筋应变迅速增大；达峰值荷载后，钢板和水平分布钢筋的塑性应变继续增大，但水平分布钢筋的塑性应变发展速度远小于钢板的塑性应变发展速度。

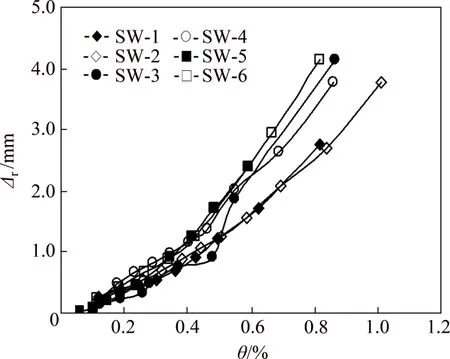
图9 残余变形曲线Fig.9 Residual deformation curves

3 受剪承载力计算

3.1 规范规定

图10 钢板主应变Fig.10 Principal strains of steel plate

图11 水平分布钢筋应变Fig.11 Strains of horizontal reinforcement

根据JGJ 3—2010“高层建筑混凝土结构技术规程”[21]和JGJ 138—2016“组合结构设计规范”[22]可知，钢板混凝土剪力墙的斜截面受剪承载力由墙体混凝土、水平分布钢筋、型钢翼缘和钢板共同承担，采用叠加的方法按下式计算：

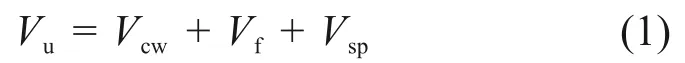
式中：Vcw为钢筋混凝土截面提供的受剪承载力；Vf为型钢翼缘截面提供的受剪承载力；Vsp为钢板截面提供的受剪承载力，

ft，fyv，fa和fsp分别为混凝土轴心抗拉强度、水平分布钢筋抗拉强度、型钢抗压强度和钢板抗拉强度；bw和hw0分别为腹板墙厚度和腹板墙截面有效高度；N为腹板墙承受的轴压力，本文试件未施加轴压力，取N=0；Aw为T形或I形截面剪力墙腹板面积，矩形截面时取A；A，Ash，Aa1和Asp分别为剪力墙全截面面积、腹板墙同一高度水平分布钢筋的截面积、剪力墙一端所配型钢的截面积和钢板截面积；s为水平分布钢筋间距；λ为剪跨比，当λ<1.5 时，取λ=1.5。

3.2 本文试件的受剪承载力

试件的受剪承载力计算值和试验值对比如表4所示。由表4可见：低剪跨比内嵌钢板−混凝土组合剪力墙的受剪承载力计算值约为试验值的83.8%，计算值低于实测值的7.5%～30.2%。由规范JGJ 3—2010和JGJ 138—2016中计算方法所得计算结果偏于安全，这主要是因为规范在计算剪跨比低于1.5 的构件的受剪承载力时，剪跨比均取为1.5，未考虑剪跨比的影响。

表4 计算值与试验值比较Table 4 Comparisons between calculations and test results

3.3 受剪承载力计算公式

对低剪跨比内嵌钢板−混凝土组合剪力墙的受剪承载力，钢筋混凝土、型钢翼缘的受剪承载力采用规范JGJ 3—2010 和JGJ 138—2016 中的公式计算，即Vcw和Vf。

实测承载力减去Vcw和Vf，得钢板的受剪承载力Vp。用本文试验结果拟合得到的计算公式为

因此，通过叠加的方式得出低剪跨比内嵌钢板−混凝土组合剪力墙的受剪承载力Vu,low的计算公式为

比较计算值与试验值可见，Vu,low/Vut的平均值为1.02，标准差为0.09，表明式(6)能够较好地拟合大部分低剪跨比内嵌钢板−混凝土组合剪力墙的受剪承载力，如图12所示。

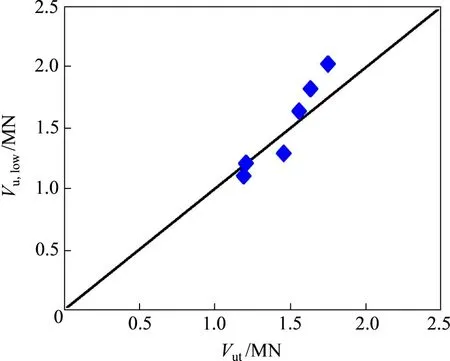
图12 受剪承载力计算值与试验值对比Fig.12 Comparisons of shear strength between prediction and experiment

4 结论

1)试件均在固定铰支座一侧的墙体发生剪切破坏。试件墙体混凝土形成斜压杆裂缝带，钢板屈服，水平分布钢筋屈曲。

2)当内嵌钢板厚度由4 mm 增大至8 mm 时，试件的受剪承载力提高20.4%～35.1%，但试件的变形能力相近。

3)当剪跨比由0.75 增大至1.25 时，试件的受剪承载力逐渐减小，且钢板厚度较小的试件受剪承载力下降幅度更大。

4)在相同位移角下，钢板厚度较大的试件与钢板厚度较小的试件的残余变形相近，表明钢板厚度对试件的残余变形没有明显的影响。

5)对于低剪跨比内嵌钢板−混凝土组合剪力墙，受剪承载力计算值约为试验值的83.8%，计算值比实测值低7.5%～30.2%，按规范JGJ 3—2010和JGJ 138—2016所得计算结果偏于安全。