基于相平面的车辆AFS与DYC可拓协调控制
2021-03-17周国忠严运兵彭文典
周国忠,严运兵,杨 勇,彭文典
(武汉科技大学汽车与交通工程学院,湖北 武汉,430065)
在汽车主动安全系统相关领域,稳定性控制一直是研究重点,目前较为成熟并已进入商用的技术有制动防抱死系统(antilock brake system, ABS)、驱动防滑系统(acceleration slip regulation, ASR)、主动前轮转向(active front-wheel steering, AFS)和直接横摆力矩控制(direct yaw-moment control,DYC)等[1]。
AFS和DYC的调控实质都是改变车辆的横摆力矩,但二者的作用机理有所不同。AFS依赖于轮胎侧向力,而DYC则由轮胎纵向力决定。由于轮胎力受到附着椭圆的限制,轮胎纵向力要比侧向力有更多的裕度[2],即轮胎侧向力饱和时,纵向力仍可能有较大的利用空间。因此将DYC与AFS集成能进一步增加转向横摆力矩的裕度,从而提高极限工况下车辆的行驶稳定性。
目前,主动转向与横摆力矩的协调控制吸引了研究人员的大量关注。文献[3]利用模糊控制理论对汽车的主动后轮转向与横摆力矩进行了联合控制,虽然该方法在一定程度上考虑了系统间的耦合关系,但其控制策略过于依赖专家经验。文献[4-5]均提出了主动转向与DYC的协调控制策略,为了控制的连贯性以及避免控制目标之间的冲突,根据专家意见设计隶属函数过渡线或基于汽车行驶稳定性指标设计调度参数,对主动转向的退出和直接横摆力矩控制的介入时机以及强度进行了设计,并通过仿真验证了协调控制策略在稳定性方面优于单独的主动转向控制。然而上述研究并未对主动转向的退出以及直接横摆力矩控制的介入时机进行理论分析,主动转向可能存在失效区,降低了控制效果。文献[6-7]应用可拓学原理,设计了可拓协调控制器,汽车操纵稳定性得到显著提高。可拓学中的关联度函数能定量、客观地描述事物具有某种性质的程度以及质变与量变的过程[8],能为协调控制器的设计提供量化参考。
为了合理设定AFS退出以及DYC介入的时机和强度,本文设计了基于相平面的AFS与DYC可拓协调控制系统。在上层控制器中,以轮胎侧偏特性线性极限和β相平面稳定域边界作为依据,将论域划分为经典域、可拓域和非域,为两种控制器的介入与退出界定时机。基于所划分的论域,运用可拓学理论求解关联度函数,并利用其确定控制器间的协调权重,即介入强度。在下层控制器中,主动前轮转向控制和直接横摆力矩控制均采用粒子群PID控制算法加以实现,其中直接横摆力矩以单轮制动方式产生,并以最小制动力作为分配依据。最后利用Simulink与CarSim建立联合仿真试验平台,对所提出的可拓协调控制系统进行仿真验证。
1 整车模型
1.1 整车动力学模型
基于某型号轿车,忽略空气阻力以及转向系统和悬架系统的影响,并考虑轮胎的非线性特性,建立扩展的二自由度整车模型,如图1所示。

图1 整车模型
整车系统运动方程为:
(1)
(2)
式中:β为质心侧偏角;r为横摆角速度;u为纵向车速;v为侧向车速;δf为前轮转角;m为整车质量;IZ为转动惯量;Lf为质心至前轴的距离;Lr为质心至后轴的距离;Fyi(i=1,2,3,4)为轮胎侧向力。
1.2 非线性轮胎模型
由于车辆失稳发生在轮胎的非线性域内,建立轮胎模型时需要考虑其非线性,因此本文采用简化的MF(magic formula)公式[9]对轮胎的实际侧偏特性进行拟合,如图2所示,其拟合公式如下:
Fyi=μFzisin[1.358arctan(0.1936αi)]
(3)
式中:μ为路面附着系数;Fzi为轮荷;αi为轮胎侧偏角;i=1,2,3,4。

图2 实际侧偏特性的拟合
2 可拓协调控制系统的设计
2.1 系统结构
AFS与DYC可拓协调控制系统分为上、下两层,如图3所示。其中,上层为AFS与DYC的功能协调层,下层为AFS控制器和DYC控制器。上层控制器为可拓协调控制器,其工作流程如图4所示。为实现AFS和DYC协调控制,要关注如下两个方面:一是确定直接横摆力矩控制的介入以及主动前轮转向控制的退出时机,即如何划分论域;二是确定主动前轮转向控制与直接横摆力矩控制的介入强度,即如何确定协调控制的权重系数γAFS和γDYC。
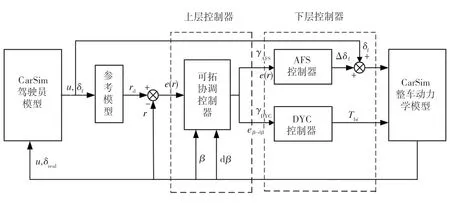
图3 AFS与DYC可拓协调控制系统框图

图4 可拓协调控制器工作流程
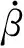
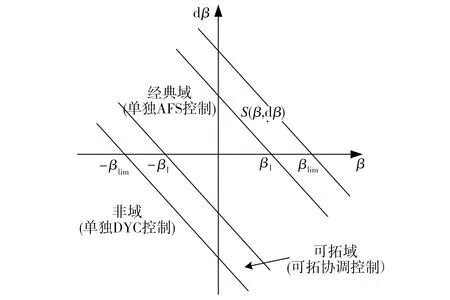
图5 论域的划分
由于关联度函数是基于车辆行驶状态进行计算的,可定量表征车辆行驶稳定性,故本文根据关联度函数来确定主动前轮转向权重系数γAFS和直接横摆力矩控制权重系数γDYC。
下层控制器中,将上层控制器输出的协调权重系数γAFS和γDYC分别输入AFS控制器和DYC控制器,获得补偿前轮转角Δδf和附加横摆力矩ΔM。同时,附加横摆力矩以单轮制动方式产生,并以最小制动力作为分配依据。
2.2 上层控制器设计
可拓协调控制器的建立分为如下几个步骤:
(1)特征状态提取
β相图能反映车辆的行驶稳定性,在汽车控制领域应用较为广泛[10-12],因此本文选用车辆的实际质心侧偏角及其变化速度组成特征状态S(β,dβ),用来描述车辆的行驶状态。
(2)论域划分
由于非域描述的是车辆的失稳状态,这与β相图失稳域相对应,因此本文选用β相图失稳域边界作为非域边界。
通过前面已建立的扩展二自由度整车模型,得到μ=0.3、u=80 km/h时的β相图,并对其进行稳定域与失稳域边界的划分,结果如图6所示。由边界线可得非域表达式为:
(4)
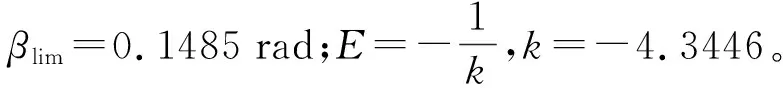

图6 β相图稳定域的划分
延用已建立的扩展二自由度整车模型,在μ=0.3、u=80 km/h的条件下以逐渐增大的斜坡函数作为前轮转角输入,观察前轮转角与横摆角速度增益Gr的关系,结果如图7所示。

图7 前轮转角与横摆角速度增益的关系
确定在轮胎侧偏特性线性极限下的前轮转角δf0,并将该转角回代到模型中求解此转角下的稳态质心侧偏角β1,结果为β1=0.0311rad。将过(±β1,0)平行于非域边界的直线作为经典域边界。
(3)关联度计算
特征量Ψ(S)是由特征状态确定的,表征了车辆的行驶稳定性,其表达式为:
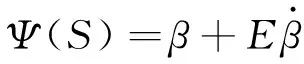
(5)
因此,用特征量描述车辆的行驶状态可将二维论域简化为一维论域,结果如图8所示。

图8 一维论域
在可拓学中,可拓距是指点与区间之距,描述了点与区间的位置关系[8]。根据其定义,任意特征量到标准正域X=[-β1,β1]的可拓距为:
ρ(Ψ,X)=|Ψ|-β1
(6)
同理,任意特征量到正域X0=[-βlim,βlim]的可拓距为:
ρ(Ψ,X0)=|Ψ|-βlim
(7)
最终确定关联度函数:
(8)
其中,
D(Ψ,X,X0)=ρ(Ψ,X0)-ρ(Ψ,X)
(9)
(4)控制模式的划分及协调权重的确定
单控模式M1:当K(Ψ)≥1时,其对应的特征状态属于经典域。轮胎侧偏特性处于线性区,AFS对车辆的操纵稳定性有较好的控制效果,且响应迅速,因此仅采用AFS进行控制。在该模式下,取AFS权重γAFS=1、DYC权重γDYC=0。
联控模式M2:当1>K(Ψ)>0时,其对应的特征状态属于可拓域。车辆趋于失稳,且轮胎侧偏特性进入非线性区,AFS的调控能力受到限制,因此需要DYC介入,来弥补AFS的不足。K(Ψ)是基于特征状态求解的关联度函数,可定量表征车辆行驶稳定性情况,并且特征状态远离经典域时K(Ψ)值减小的变化趋势符合AFS权重分配原则,故在该模式下,取γAFS=K(Ψ)、γDYC=1-K(Ψ)。
单控模式M3:当K(Ψ)≤0时,其对应的特征状态属于非域,车辆处于失稳状态。AFS退出工作,仅保留DYC控制车辆稳定性。在该模式下,取γAFS=0、γDYC=1。
2.3 下层控制器设计
2.3.1 主动前轮转向控制器
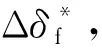
e(r)=rd-r
(10)
(11)
(12)
由于传统的PID控制无法满足对车辆动态系统的稳定性控制要求,因此本文在传统PID控制的基础上引入粒子群算法,根据输入量的偏差在线优化系统PID参数,工作原理如图9所示。PSO算法在每一次迭代过程中,粒子通过个体极值和全局极值更新自身速度和位置,更新公式如下[14]:
(13)
(14)
式中:k为迭代次数;i=1,2,…,N,其中N为粒子数;d=1,2,…,D,其中D为问题维度;Vid为粒子速度;w为惯性权重;c1、c2为加速因子;r1、r2为随机系数,取值范围为[0,1];Pid和Pgd分别为粒子的个体最优位置和全局最优位置;Xid为粒子的矢量位置。

图9 基于PSO的PID控制系统结构框图
为了能均衡粒子群优化算法的全局探索和局部搜索能力,加快算法的求解速度,将惯性权值设定为线性递减形式:
(15)
式中:wmax为最大惯性权重;wmin为最小惯性权重;n为当前迭代次数;nmax为最大迭代次数。
计算过程中,设定加速因子c1和c2的值均为2,惯性权重取值范围为[0.3,0.9],种群个数为30,最大迭代次数为50。
2.3.2 直接横摆力矩控制器
直接横摆力矩控制应用于可拓域与非域,以弥补主动前轮转向控制的不足。该控制基于论域设计,以车辆回归稳定所需最小附加横摆力矩为设计目标,选用车辆特征状态到经典域的距离作为调控量,同样采用粒子群PID算法计算附加横摆力矩ΔM*,并结合权重系数γDYC确定实际值ΔM,最终以车轮最小制动力作为分配依据,设计制动力矩分配规则。设计步骤如下:
(1)求解附加横摆力矩
由二维论域与一维论域之间的关系不难发现,基于二维论域的调控量为基于一维论域调控量的倍数。基于一维论域的附加横摆力矩计算公式如下:
eβ-dβ=|Ψ(s)|-β1
(16)
(17)
ΔM=γDYCΔM*
(18)
(2)制动力矩分配
文献[15]指出:对内侧车轮施加相同的制动力时,后轮产生更大的内向横摆力矩;对外侧车轮施加相同的制动力时,前轮产生更大的外向横摆力矩。这与文献[16]中横摆力矩与制动力的关系曲线所描述的相一致。因此,本文以单轮制动的最小制动力作为分配依据,给出如表1所示的制动力分配规则。

表1 制动力分配规则
3 仿真分析
利用Simulink与CarSim建立联合仿真试验平台,对基于相平面的AFS与DYC可拓协调控制系统进行仿真验证。由于本文重点是根据轮胎特性研究在极限工况下通过直接横摆力矩控制来弥补主动前轮转向对车辆稳定性控制的不足,因此选择低附单移线工况和低附阶跃转向工况进行仿真试验。整车参数如表2所示。

表2 整车参数
3.1 低附单移线试验工况
在单移线工况下,方向盘转角按正弦规律变化,如图10所示。设定车辆行驶速度为80km/h,路面附着系数为0.3,在第3s时方向盘输入幅值为90°、频率为0.33Hz的正弦变化角度,仿真结果如图11所示。
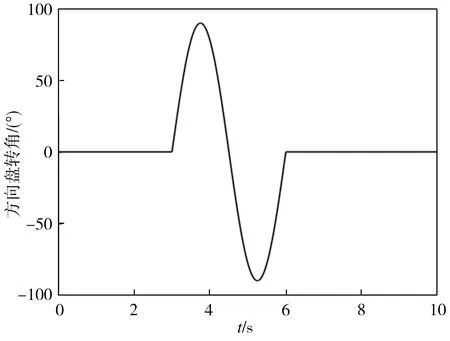
图10 低附单移线工况下的方向盘转角
从仿真结果可以看出:①无控制时,车辆的实际横摆角速度、质心侧偏角以及相轨迹响应均存在发散,车辆发生失稳。造成车辆失稳的根本原因是轮胎侧向力的饱和特性。②采用主动前轮转向控制时,车辆的实际横摆角速度和实际质心侧偏角都有了一定程度的改善,但与理想值仍有较大偏离,且相轨迹区域较大(见图11(c)),对车辆的稳定性控制欠佳。这是因为在极限工况下,车辆前轮侧向力一直处于饱和状态,仅有AFS控制时车辆后轮侧向力易饱和,总侧向力无法支持车辆理想的横摆运动(见图11(d))。③采用可拓协调控制时,由于DYC控制的介入(见图11(g)),差动制动产生了一部分横摆力矩(见图11(f)),使得前轮侧向力饱和时后轮侧向力仍未超过阈值(见图11(e))。此时车辆的实际横摆角速度响应对理想横摆角速度有较好的跟随效果,实际质心侧偏角响应相较于采用单一的主动前轮转向控制时也有明显的改善,并且相轨迹区域最小,表现出良好的稳定性控制效果。
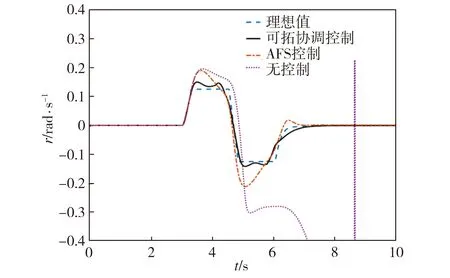
(a)横摆角速度响应
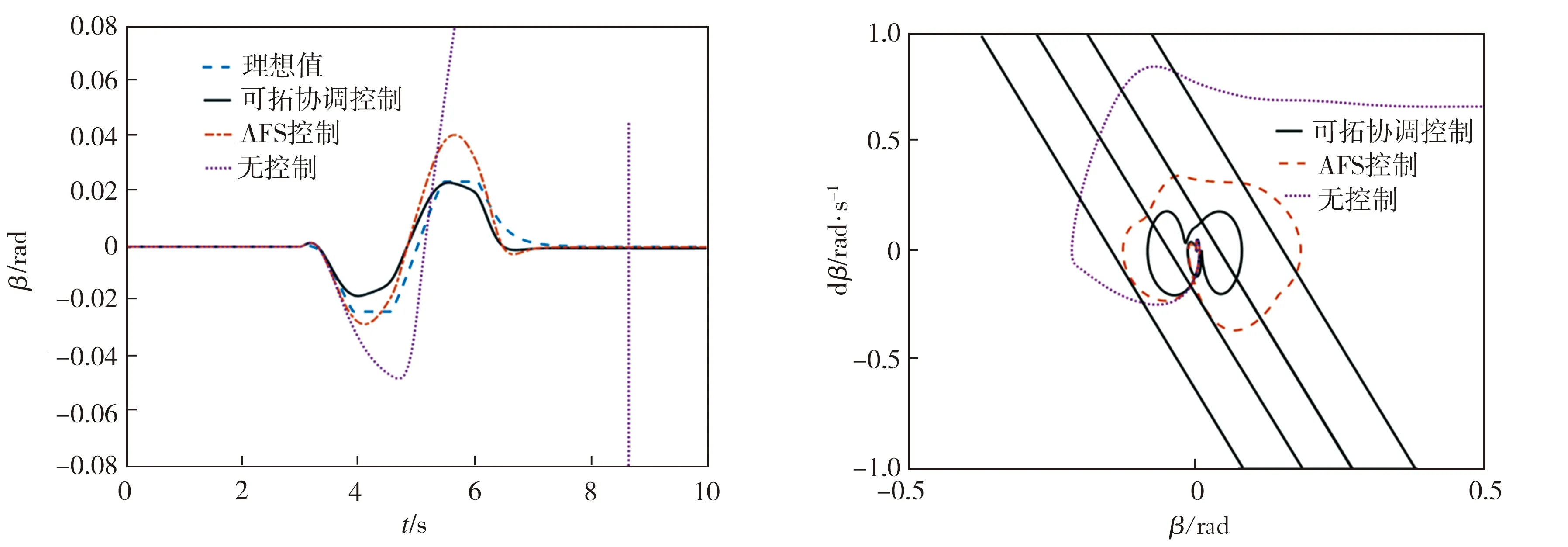
(b)质心侧偏角响应 (c)不同控制模式下的相轨迹
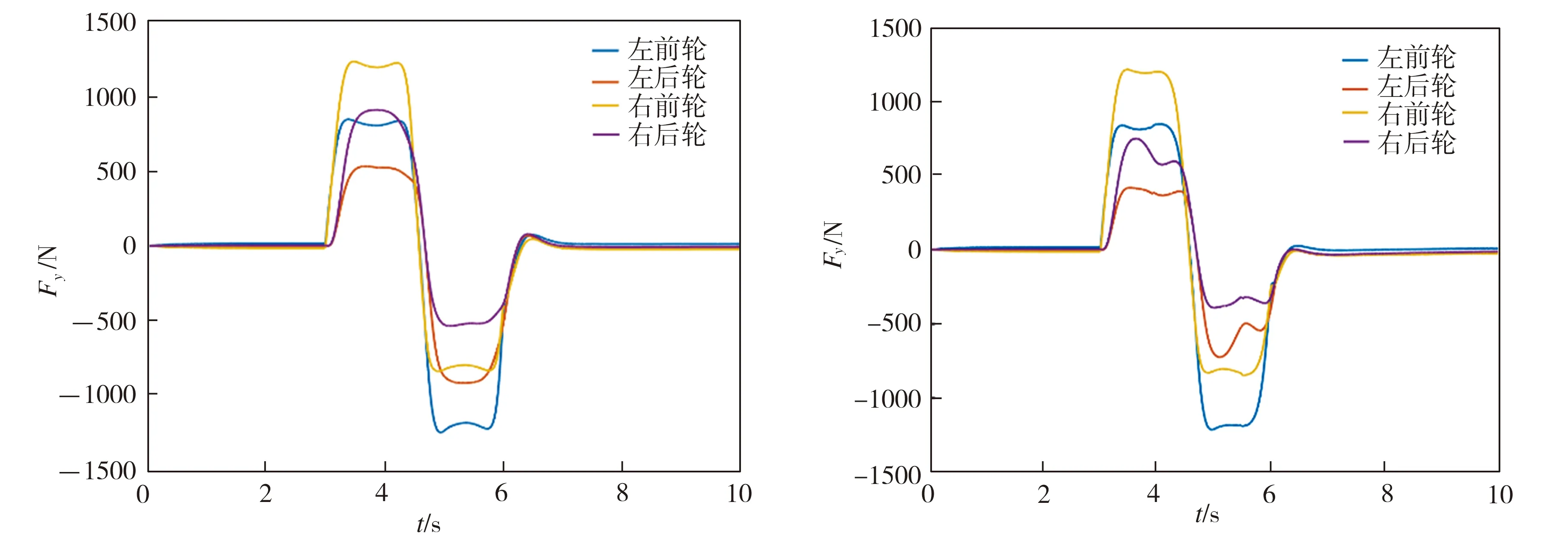
(d) AFS控制下的轮胎侧向力 (e) 协调控制下的轮胎侧向力

(f) 协调控制制动力矩 (g)AFS与DYC协调控制信号分配
3.2 低附阶跃转向试验工况
在CarSim中建立行驶工况,设定路面附着系数为0.3,恒定车速为80 km/h。仿真开始第3 s后进入阶跃转向工况,阶跃转向角为90°,如图12所示,仿真结果如图13所示。
从仿真结果可以看出:①在无控制时车辆已经明显发生失稳,实际横摆角速度和实际质心侧偏角响应幅值均较大并且存在发散趋势。②采用主动前轮转向控制时,实际横摆角速度响应幅值明显降低且曲线最终收敛,但超调量偏大,达到稳态的时间偏长,抖振较为明显,稳定时间约7.9 s,稳态值为0.135 rad/s。实际质心侧偏角有同样的响应趋势,稳定时间约为6.8s,稳态值为0.0251 rad。③采用可拓协调控制时,与单一的主动前轮转向控制相比,车辆的实际横摆角速度响应超调量下降了15.2%,达到稳态的时间更短,抖振现象明显减弱,稳定时间约为4.9 s,且稳态值更接近理想值,为0.128 rad/s。此时的实际质心侧偏角也得到了很好的控制,抖振较小,收敛较快,在5.2 s时达到稳态且稳态值为0.0216 rad。

图12 低附阶跃转向工况下的方向盘转角
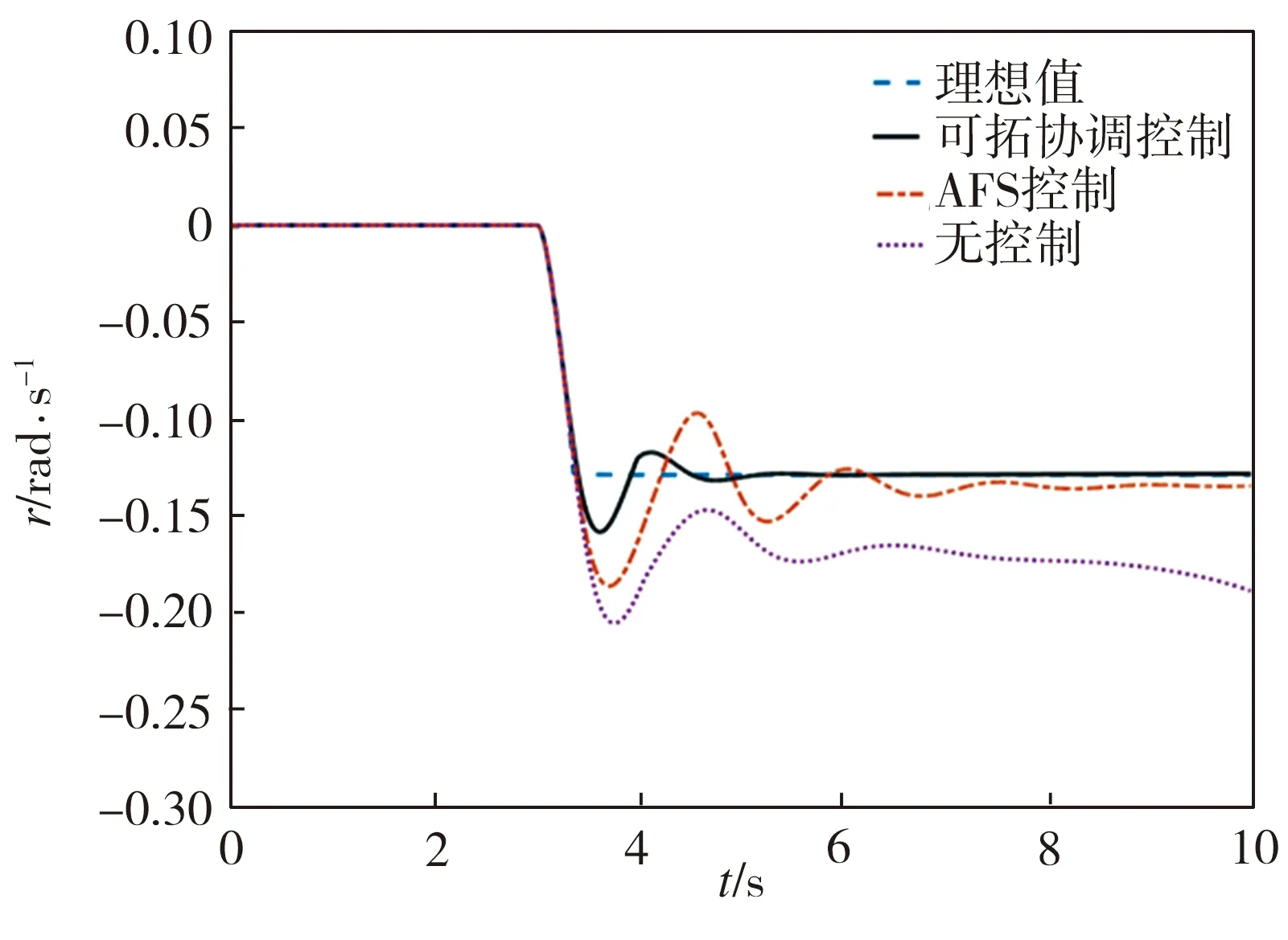
(a)横摆角速度响应

(b)质心侧偏角响应
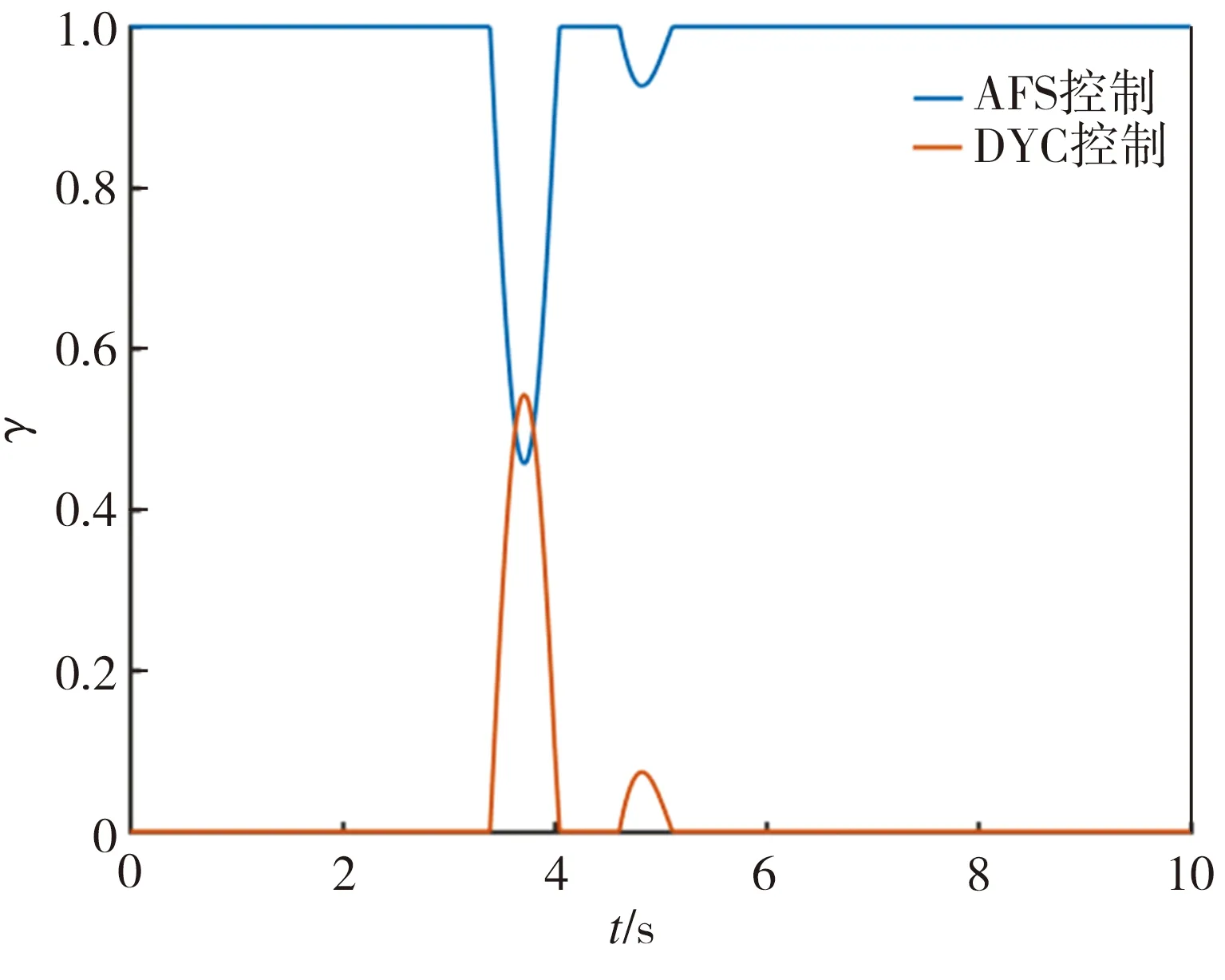
(c)AFS与DYC协调控制信号分配
4 结语
本文通过分析轮胎特性对主动前轮转向控制适用范围的限制,建立了基于相平面的AFS与DYC可拓协调控制系统。选用质心侧偏角和质心侧偏角速度作为特征状态,依据轮胎侧偏特性线性极限以及β相图稳定域边界来划分论域,利用可拓学理论计算关联度函数并最终确定各控制器协调权重系数。
采用粒子群PID控制算法设计下层控制器,结合上层输出权重系数,分别得到实际补偿前轮转角和实际附加横摆力矩。同时,附加横摆力矩以单轮制动方式产生,并以最小制动力作为分配依据。
利用Simulink和CarSim建立联合仿真实验平台,在低附阶跃转向工况和低附单移线工况下进行仿真试验,证明采用本文提出的可拓协调控制策略能有效跟踪参考轨迹,同时可减小质心侧偏角,提高车辆的行驶稳定性。
