基于非线性支承的磁悬浮双转子系统碰摩特性研究
2021-03-17姚俊夫王念先刘明政葛萍萍
姚俊夫,王念先,刘明政,葛萍萍
(1. 武汉科技大学冶金装备及其控制教育部重点实验室,湖北,武汉,430081;2. 武汉科技大学机械传动与制造工程湖北省重点实验室,湖北,武汉,430081)
由于主动磁悬浮轴承具有无接触、无需润滑、无磨损、转速高、动态特性可调等优点,磁悬浮双转子系统(Magnetic suspended dual-rotor system, MSDS)能大大提高旋转机器的使用性能和可靠性[1-2]。转子碰摩故障是旋转机械中的典型故障,具有极大危害性,根据接触区域,碰摩故障可分成全周碰摩和偏摩[3]。在机械轴承支承的双转子系统中,文献[4-7]基于双转子试验台,建立了定点碰摩故障下双转子系统的动力学模型,研究了转速比、初始间隙和限位器曲率半径等参数对系统碰摩响应的影响,结果表明,系统参数对机械轴承支承的双转子系统碰摩响应有较明显的影响,当双转子系统发生碰摩时,响应中能观察到更多的内外转子转频的组合频率分量。
近年来,国内外研究者针对磁悬浮转子系统的碰摩和其他非线性动力学特性开展了大量研究。文献[8]研究了刚度比、圆盘偏心量、碰摩间隙等对磁悬浮双盘转子系统碰摩的影响;文献[9]研究了刚度比、库伦摩擦系数、比例系数和微分系数等对磁悬浮转子系统碰摩的影响;文献[2,10]基于拉格朗日方程建立了磁悬浮双转子系统动力学模型,分析了转速比、中介轴承刚度等对系统非线性动力学行为的影响;文献[11]对磁悬浮双转子系统碰摩故障下的振动特性及接触过程进行分析,研究了控制参数对系统碰摩的影响。由此可见,磁悬浮转子系统中,系统运行参数和控制参数均会对其碰摩和非线性响应产生影响。但这些文献中,磁悬浮轴承的支承力模型忽略了磁性材料非线性、系统漏磁和磁饱和等非线性因素的影响,其往往为线性化模型,无法全面展示磁悬浮转子系统的碰摩动力学响应特性。
而实际运行过程中,双转子系统的复杂激励会导致磁悬浮轴承的工作点发生较大范围变化,此时,系统漏磁和磁饱和等非线性因素成为影响磁悬浮轴承支承特性的关键,磁悬浮轴承的支承特性呈明显的非线性特征[12-16],从而导致系统的碰摩特性发生改变,但目前尚缺乏对非线性支承特性下磁悬浮双转子系统的碰摩特性的研究。
为此,本文在磁悬浮轴承的非线性支承特性基础上,采用Lankarani-Nikravesh 模型和库伦模型,建立了基于非线性支承的磁悬浮双转子系统的动力学模型,研究了基于非线性支承的磁悬浮双转子系统的定点碰摩特性,并分析了控制参数对系统碰摩特性的影响,研究结果可为磁悬浮双转子系统的设计和运行提供参考。
1 动力学模型
基于航空发动机的结构特点设计的磁悬浮双转子结构如图1所示。为方便后续研究,特将不考虑磁悬浮轴承漏磁、磁饱和等的磁悬浮双转子系统称为常规磁悬浮双转子系统,而将考虑了磁悬浮轴承漏磁、磁饱和等非线性因素的系统称为非线性磁悬浮双转子系统。

图1 磁悬浮双转子结构示意图
如图1所示,基于有限元分析法,将该磁悬浮双转子系统离散成9个节点,包括内转子5个节点和外转子4个节点。内外转子之间通过中介轴承连接。此磁悬浮双转子系统有3个磁悬浮轴承和4个刚性圆盘。本研究采用如下假设:①忽略扭振和轴向振动的影响,仅仅考虑径向振动的自由度;②不考虑转子自身重力对系统造成的影响;③将中介轴承等效成刚度和阻尼,施加到动力学模型对应节点上。磁悬浮双转子系统的主要结构参数见表1。
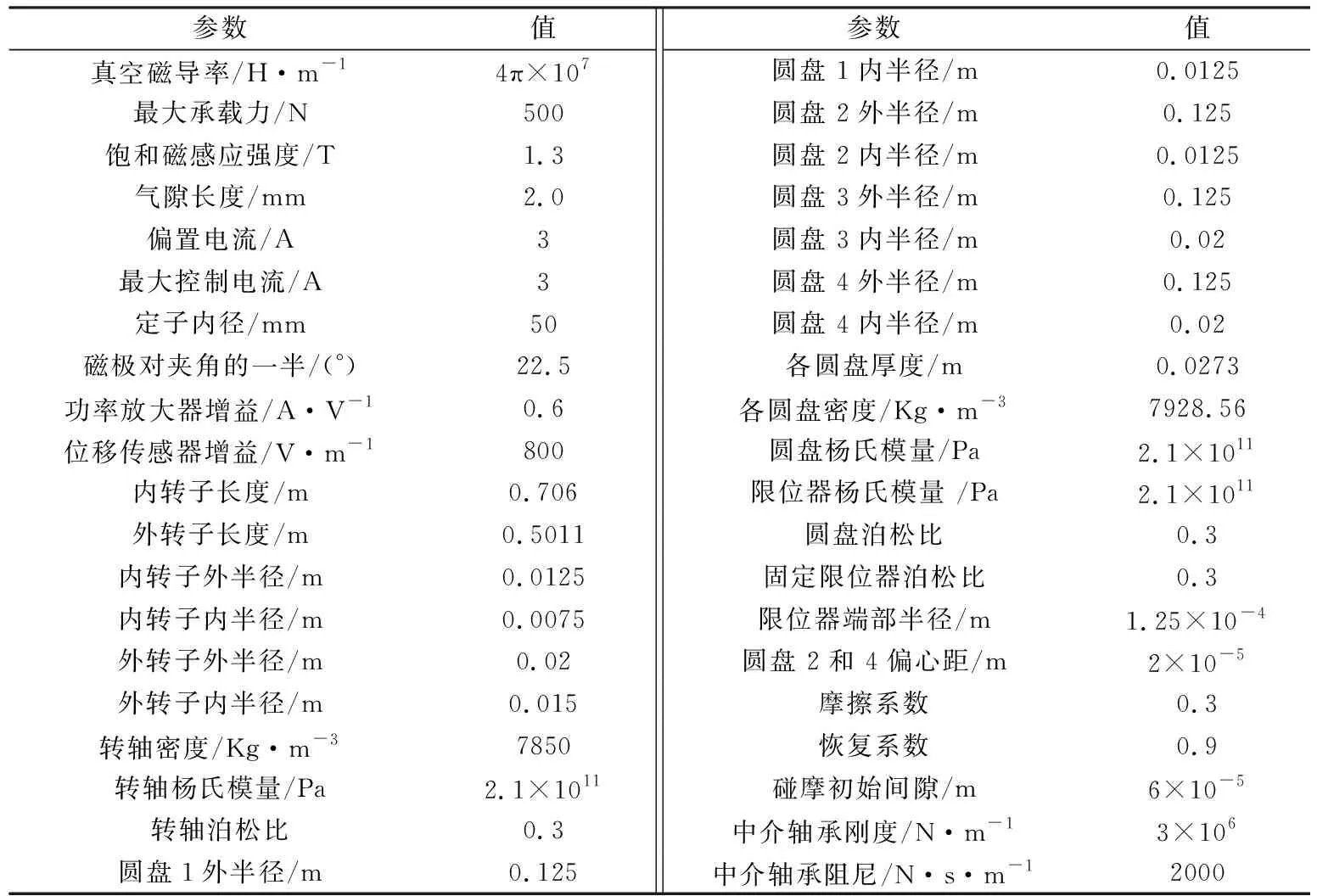
表1 磁悬浮双转子系统的主要结构参数
1.1 磁悬浮轴承支承模型
本文采用差动控制的八磁极径向磁悬浮轴承,其在某方向上的控制原理图如图2所示,单个磁极的等效磁路图(Equivalent magnetic circuit, EMC)如图3所示[16]。

图2 控制原理图
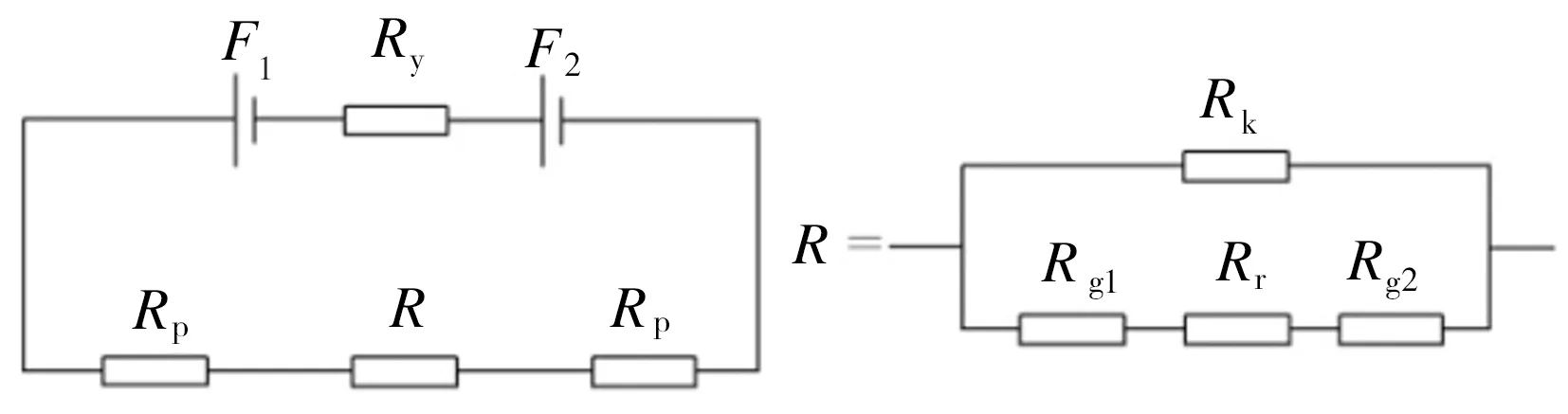
图3 单个磁极的等效磁路图
图2和图3中,F1和F2表示磁极相邻线圈中的磁动势;Ib和Ic分别为偏置电流和控制电流;g0为气隙长度;Ry、Rp、Rr分别表示的是定子磁轭磁阻、磁极磁阻、转子磁阻;Rk为漏磁磁阻;Rg1、Rg2为此磁极处的气隙磁阻。
目前对磁悬浮轴承的研究中,通常将磁悬浮轴承的支承特性进行线性化处理,但在实际情况中,系统的漏磁和磁饱和等非线性因素会对磁悬浮轴承的支承特性造成显著影响。本文将磁悬浮轴承支承力模型分为两种情况讨论:
(1)常规支承力模型:不考虑漏磁及磁饱和等非线性因素对磁悬浮轴承承载特性的影响。图3中Ry、Rp、Rr和Rk均为零,只存在气隙磁阻Rg1和Rg2,此时磁悬浮轴承的支承力特性可参考文献[17]。
(2)非线性支承力模型:在实际情况中,磁悬浮轴承受到外载和运行状况的影响,系统的气隙漏磁和磁性材料的非线性磁导率不能忽略。此时,Ry、Rp、Rr、Rk、Rg1和Rg2均不为零,则x方向上的电磁力[16]:
(1)
式中:μ0为真空磁导率;α为磁极对夹角的一半;Ap为磁极面积;Ф1和Ф3分别为两侧通过磁路气隙中的磁通,根据图3可得:
(2)
式中:N为线圈匝数;Ry、Rp、Rr、Rk、Rg1、Rg2、Rg3、Rg4(Rg3和Rg4表示另一侧磁极处的气隙磁阻)计算方法可以由文献[16]得到。
图4为两种支承力模型和有限元模型(计算方法参考文献[15])计算获得的承载力曲线。由于有限元结果具有较高的计算精度[15],本文利用有限元计算结果对两种模型计算的支承力准确性进行验证。
图4中,e是径向偏心距与气隙长度的比值。由图4可以看出,不同e值下,磁悬浮轴承的支承特性均存在明显的非线性特征,非线性支承力模型的计算精度明显优于常规支承力模型的精度;当控制电流较大时,磁悬浮轴承支承特性的非线性特征更加明显,这将会影响到磁悬浮双转子系统的碰摩响应。本文将非线性支承力模型融入到磁悬浮双转子系统的动力学模型中,更全面地分析了该系统的碰摩响应。

(a)e=0 (b)e=0.2
1.2 定点碰摩模型
采用Lankarani-Nikravesh模型,圆盘与固定限位器的碰摩力模型如图5所示。

图5 圆盘-固定限位器的碰摩力模型[11]
图5中,碰撞过程中的法向冲击力Fn和切向摩擦力Ft在水平方向上的投影Frx和竖直方向上的投影Fry分别为
(3)
式中:θ为碰摩时的接触角度,且
(4)
式中:kr为接触刚度;r为圆盘与限位器端部在碰撞方向上的距离;ce为恢复系数;v为圆盘在碰撞方向上的冲击速度;v0为初始冲击速度;fr为摩擦系数。
1.3 系统动力学模型
根据图1所示磁悬浮双转子系统的结构特点,磁悬浮双转子系统的运动方程为

(5)
式中:q为磁悬浮双转子系统的广义位移矩阵;M、C和K分别表示磁悬浮双转子系统的总体质量矩阵、总体阻尼矩阵、总体刚度矩阵;F为外部激励力矢量。
为考虑非线性因素对磁悬浮轴承支承特性的影响,本研究将磁悬浮轴承电磁力当作转子所受的外力来看待,即
F=Fa+Fr+Fq
(6)
式中:Fa为磁悬浮轴承的支承力矢量;Fr为碰摩力矢量;Fq为不平衡量矢量。综上所述:
(7)
式中:0表示零矩阵;k、i和j分别表示不同外部激励对应的节点。此外,在上述总体刚度矩阵和阻尼矩阵中还需在对应的节点处加上中介轴承的刚度和阻尼。
2 动力学模型验证
基于文献[4]发表的研究结果,对本文非线性支承下的动力学模型计算结果进行验证。当外载扰动较小时,磁悬浮轴承的支承特性仅在平衡点附近变化,此时磁悬浮轴承的支承特性近似呈线性,取平衡位置处磁悬浮轴承的等效刚度和阻尼等同于文献[4]中机械轴承刚度和阻尼,以保证系统的轴承特性在更换后保持不变。将文献[4]中的机械轴承均替换为磁悬浮轴承支承,此时,圆盘1竖直方向上的位移响应如图6所示,可以看出,本文采用的非线性磁悬浮双转子系统的仿真结果和文献[4]中的试验结果一致。

(a)文献[4]试验结果 (b)本文仿真结果
在碰摩条件下,文献[4]试验结果及本文仿真结果对比如图7所示,可以看出,本文非线性磁悬浮双转子系统频谱响应基本与文献[4]中的结果相一致,只是各频率分量对应的幅值有所不同,这主要是由于不平衡量位置和初始条件差异所导致的结果误差。综合上述分析可知,本文建立的非线性支承下磁悬浮双转子系统的定点碰摩动力学模型是可行的。

(a)文献[4],未碰摩
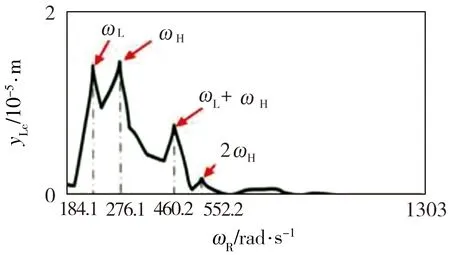
(b)文献[4],碰摩

(c)本研究,未碰摩

(d)本研究,碰摩
3 定点碰摩特性分析
3.1 磁悬浮双转子系统的动态响应分析
当磁悬浮双转子系统承受较大外载时,磁悬浮轴承呈现出较强的非线性特征,转子系统的动态响应也趋于复杂。取KP=40、KI=100、KD=0.05,内转子转速ωi=400 rad/s,转速比rs=1.2。假设固定限位器在圆盘2正上方,圆盘2处受到沿限位器方向的负载FL=250 N,图8为磁悬浮双转子系统在未碰摩和碰摩时圆盘2竖直方向上的动态响应。
图8(a)中,在未碰摩情况下,常规磁悬浮双转子系统的频谱图中只存在内外转子的转频fi和fo;而图8(b)中,由于磁悬浮轴承的非线性支承特性,非线性磁悬浮双转子系统在未碰摩时的动态响应中出现了内外转子转频的组合频率分量, 如fo-fi、2fi、fi+fo和2fo;图8(c)和8(d)中,虚线所处位置表示碰摩的初始间隙,在发生碰摩后,磁悬浮双转子系统的动态响应更加复杂,响应频谱图中出现了更多的内外转子转频的组合频率分量mfi±nfo(m,n=1,2,3,…)。

(a)未碰摩时常规磁悬浮双转子系统
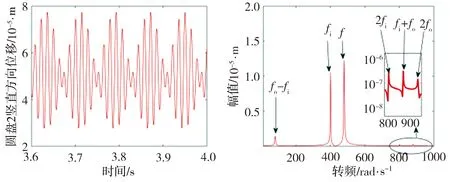
(b)未碰摩时非线性磁悬浮双转子系统

(c)碰摩时常规磁悬浮双转子系统
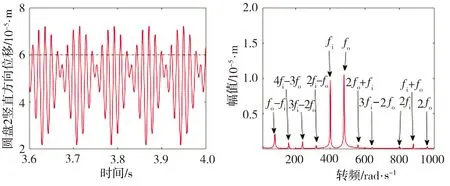
(d)碰摩时非线性磁悬浮双转子系统
图9为常规和非线性磁悬浮双转子系统在FL=0、碰摩间隙δ=1×10-5和FL=250 N、δ=6×10-5条件下的碰摩力响应。
由图9可见,在FL=0时,常规和非线性磁悬浮双转子系统在一个周期内碰摩次数和最大碰摩力基本无差别;当FL=250 N时,非线性磁悬浮双转子系统在一个周期内的碰摩次数和最大碰摩力分别为5次和74.42 N,大于常规磁悬浮双转子系统的4次和34.35 N,这意味着此时在非线性支承下系统的碰摩更加剧烈。
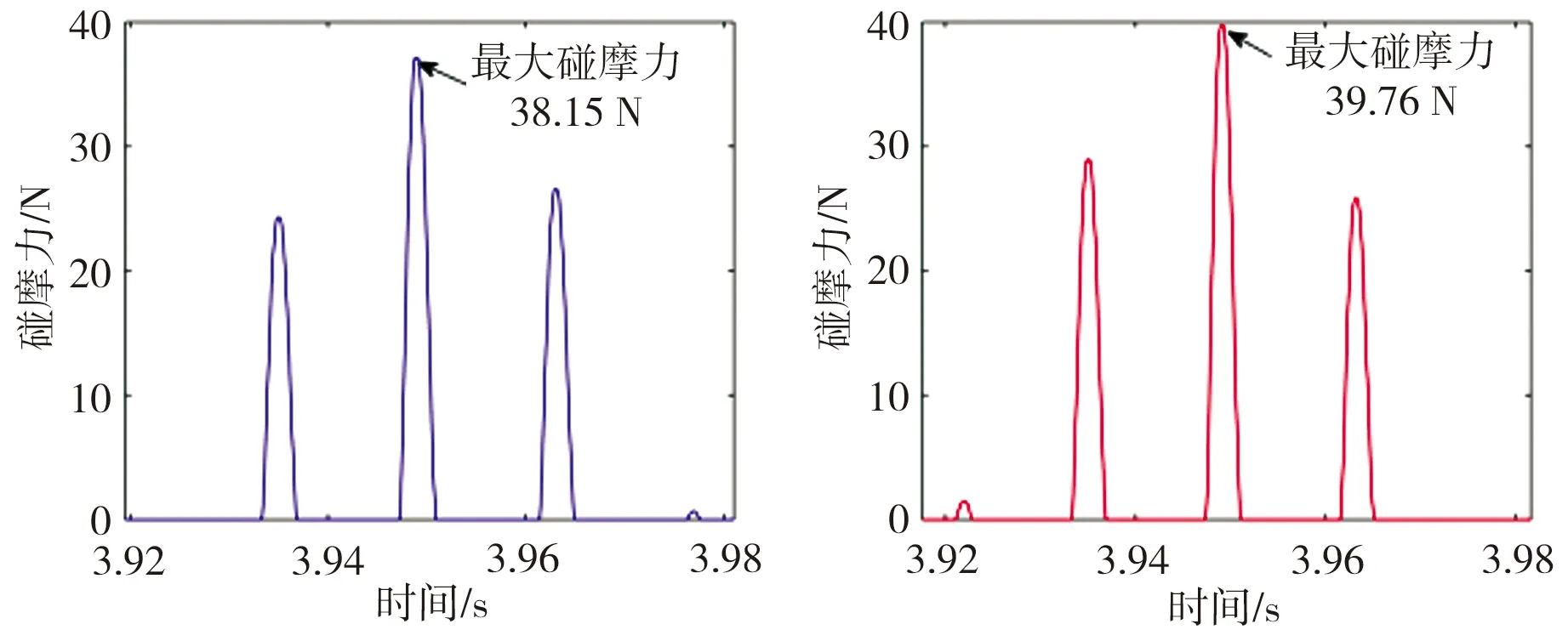
(a)常规磁悬浮系统,FL=0 (b)非线性磁悬浮系统,FL=0

(a)常规磁悬浮系统,FL=250 N (b)非线性磁悬浮系统,FL=250 N
此外,负载前后碰摩时电磁轴承处的承载力曲线也有所不同,图10为负载前后碰摩时磁悬浮轴承2竖直方向上的承载力曲线。由图10可见,未负载时,常规和非线性磁悬浮双转子系统承载力曲线基本一致;而负载之后,磁悬浮轴承的支承特性表现出明显的非线性特征,非线性磁悬浮系统的最大电流值约为2.5A,大于常规磁悬浮双转子系统最大电流值1.7 A,并且更接近电流饱和值(±3 A)。此外,非线性系统电流振幅约为1.4 A,大于常规系统的0.8 A。
综上所述,在非线性支承特性下,磁悬浮双转子系统的碰摩响应会发生明显变化,特别是在负载较大的情况下,磁悬浮轴承的非线性支承特性对系统的碰摩响应会产生明显影响。
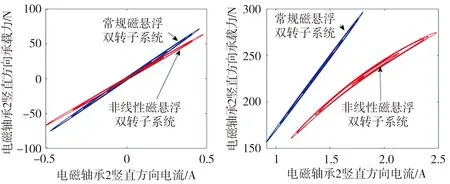
(a)FL=0 (b)FL=250 N
3.2 负载对系统碰摩特性的影响
为进一步了解非线性磁悬浮双转子系统在不同负载下的碰摩规律,不同负载FL下非线性磁悬浮双转子系统在圆盘2竖直方向处的碰摩响应瀑布图及磁悬浮双转子系统的最大碰摩力如图11所示。
由图11(a)可见,随着FL的增大,非线性磁悬浮双转子系统的瀑布图中出现了部分组合频率分量,FL增至180 N时,系统开始发生碰摩,响应中开始出现了新的组合频率分量,如4fi-3fo、3fi-2fo等;随着FL继续增大,系统的碰摩程度加剧,系统的动态响应更复杂,更多的组合频率分量被激发出来。由图11(b)可见,随着FL的增大,常规和非线性磁悬浮双转子系统的最大碰摩力均越来越大,碰摩程度越来越剧烈;另外,两磁悬浮双转子系统开始碰摩时对应的FL并不相同,常规磁悬浮双转子系统在FL=200 N时开始碰摩,并且相比于常规磁悬浮双转子系统,非线性磁悬浮双转子系统最大碰摩力变化速度更快。
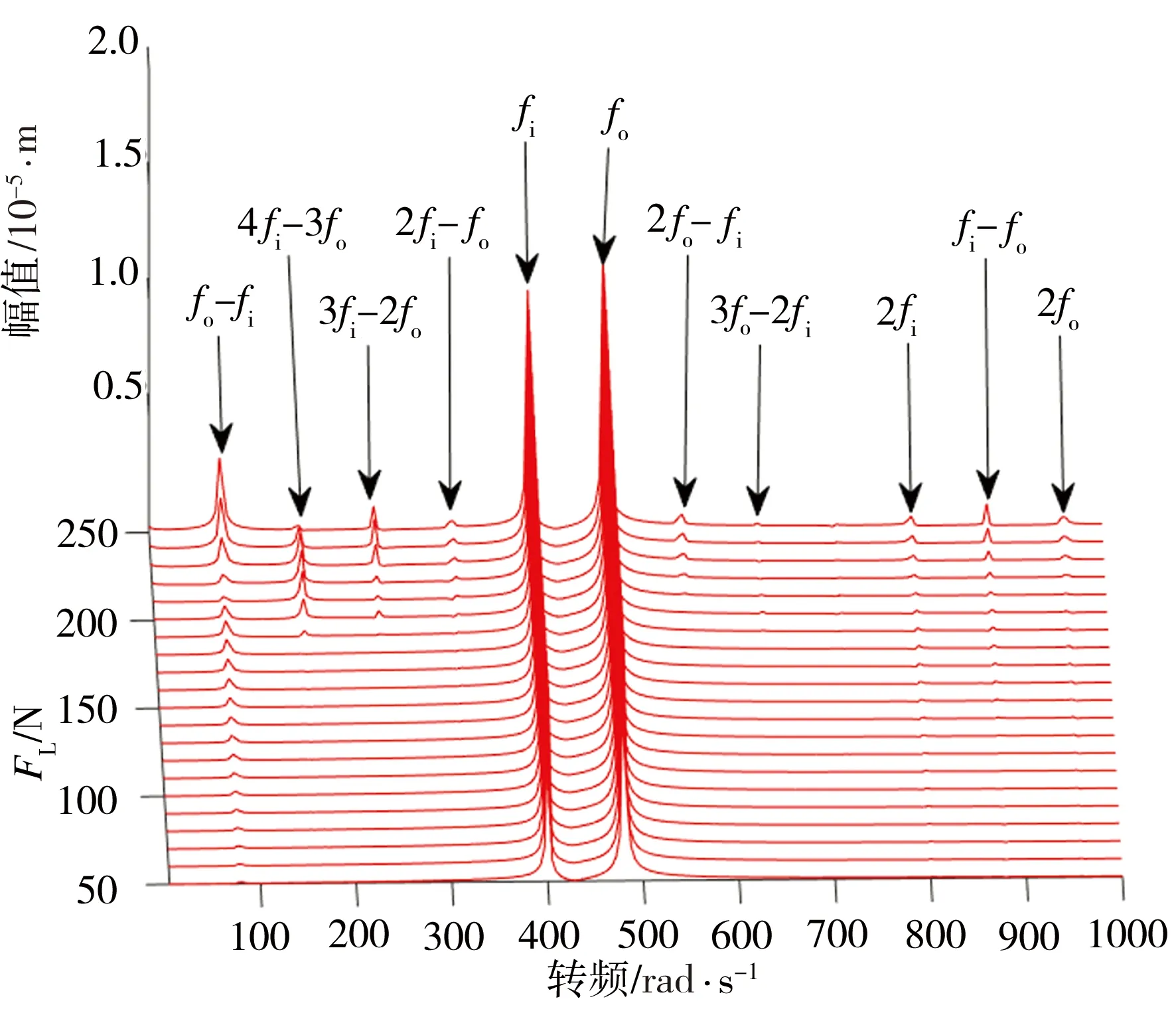
(a) 非线性磁悬浮双转子系统的碰摩响应

(b) 磁悬浮双转子系统的最大碰摩力
3.3 转子转速对系统碰摩特性的影响
在与图11相同的控制参数下,为减小磁悬浮轴承电流饱和对非线性磁悬浮双转子系统碰摩响应的影响,特取FL=200 N,图12所示为不同内转子转速ωi下非线性磁悬浮双转子系统在圆盘2竖直方向上的碰摩响应瀑布图及磁悬浮双转子系统的最大碰摩力。
由图12(a)可见,当ωi在[150, 220] rad/s时,非线性磁悬浮双转子系统振幅增大,碰摩加剧,响应瀑布图中出现了较多组合频率分量;继续增大ωi至350 rad/s时,系统重新开始碰摩。在图12(b)中,在ωi为[150, 220] rad/s时,常规和非线性磁悬浮双转子系统均发生碰摩,且非线性磁悬浮双转子系统发生碰摩时对应的最大碰摩力更大;此外,当ωi为350 rad/s时,常规磁悬浮双转子系统并未发生碰摩,这表明在外载一定的条件下,磁轴承的非线性支承使系统发生碰摩时对应转速范围更宽,系统碰摩更严重。

(a) 非线性磁悬浮双转子系统的碰摩响应

(b) 磁悬浮双转子系统的最大碰摩力
3.4 控制参数对系统碰摩特性影响
在结构参数和运行工况确定的情况下,控制参数也会对非线性磁悬浮双转子系统的碰摩响应产生影响。本节主要研究在PID控制下,非线性磁悬浮双转子系统在较大外载下碰摩响应随控制参数的变化规律。
取KI=100、KD=0.03、ωi=500 rad/s,图13为不同比例系数KP下非线性磁悬浮双转子系统圆盘2竖直方向上的碰摩响应瀑布图和磁悬浮双转子系统在此KP区间下的最大碰摩力。
由图13(a)可见,KP对非线性磁悬浮双转子系统的碰摩响应会产生明显影响,不同KP值下非线性磁悬浮双转子系统的碰摩程度有所不同;当KP处于[30, 50]时,系统的振幅增大,碰摩程度加剧,碰摩响应中存在较多的组合频率分量。

(a) 非线性磁悬浮双转子系统的碰摩响应

(b) 磁悬浮双转子系统的最大碰摩力
由图13(b)可知,常规和非线性磁悬浮双转子系统在此KP区间的最大碰摩力均存在峰值,两个系统最大碰摩力峰值处对应的KP值不相同,非线性磁悬浮双转子系统最大碰摩力的最大值为48.62 N(KP=40),大于常规的磁悬浮双转子系统最大碰摩力的最大值26.52 N(KP=32),且非线性磁悬浮双转子系统发生碰摩对应的KP区间更宽,表明磁悬浮轴承的非线性支承特性使磁悬浮双转子系统的碰摩程度加剧。实际情况中应合理选择KP值,以避开系统碰摩严重区间。
取与图13相同的运行工况,当KP=40、KI=100时,不同微分系数KD下磁悬浮双转子系统圆盘2竖直方向上的碰摩响应瀑布图和磁悬浮双转子系统的最大碰摩力如图14所示。
由图14(a)可见,KD对非线性磁悬浮双转子系统定点碰摩响应有显著影响,当KD较小时,系统振幅增大,碰摩现象严重,系统稳定性下降,在频谱图低频率段出现了丰富的组合频率分量;随着KD增大,系统抑制振动能力增强,系统的碰摩程度减缓,部分组合频率分量消失。由此可见,较大的KD值有助于减小系统振动,减轻系统的碰摩程度。从图14(b)可以看出,常规和非线性磁悬浮双转子系统的最大碰摩力随KD的增大而减小,表明系统的碰摩程度随着KD的增大而减小;此外,非线性磁悬浮双转子系统的最大碰摩力更大,特别是在KD较小的情况,当KD=0.060时,常规磁悬浮双转子系统已结束碰摩,而非线性磁悬浮双转子系统还处于间隙式碰摩状态,这表明磁悬浮轴承的非线性支承特性加剧了磁悬浮双转子系统碰摩程度。

(a) 非线性磁悬浮双转子系统的碰摩响应

(b) 磁悬浮双转子系统的最大碰摩力
取图14相同的运行工况,即KP=40、KD=0.03,不同积分系数KI下非线性磁悬浮双转子系统圆盘2竖直方向上的碰摩响应瀑布图和磁悬浮双转子系统的最大碰摩力如图15所示。由图15可见,KI对磁悬浮双转子系统碰摩响应影响较小,随着KI的增大,常规和非线性磁悬浮双系统碰摩时的最大碰摩力均缓慢增大,系统的稳定性变差。可见,在满足系统稳态控制精度的情况下应选择较小的积分系数。

(a) 非线性磁悬浮双转子系统的碰摩响应

(b) 磁悬浮双转子系统的最大碰摩力
4 结论
(1)磁悬浮轴承的非线性支承特性对磁悬浮双转子系统的碰摩会造成较大影响,特别是系统受到较大的外载荷时,非线性支承特性下的系统碰摩区间更宽,碰摩区间内对应的最大碰摩力更大,碰摩程度更加严重;系统发生碰摩时,响应中可观察到内外转子转频(fi和fo)的组合频率分量mfi±nfo(m,n=1,2,3,…),且碰摩程度越剧烈,系统激发的组合频率分量越多。
(2)在非线性支承下,比例系数和微分系数对非线性磁悬浮双转子系统定点碰摩有显著影响。合理选择比例系数和较大的微分系数可有效减小系统的碰摩程度,此外,在满足系统稳态控制精度的情况下应选择较小的积分系数。
