以数学实验深化数学理解

黄芬 张建国

摘要：数学实验将“做”“学”“思”合一，有效丰富与改进了数学学习方式，引导学生开展身心合一的具身认知，从而加深学生的数学理解。小学数学教学中，教师可依据不同的教学内容，根据学生已有经验，积极开发与实施不同形式的数学实验，深化学生的数学理解。为了聚焦知识理解，在结论验证、规律探索时嵌入单项实验;为了促进方法理解，开展串联式与并联式的组块实验;为了丰富经验理解，实施多角度、多内容、多学科的融合实验。

关键词：数学实验;数学理解;单项实验;组块实验;融合实验

实践表明，学生学习方式的不同，决定了数学理解层次的不同。数学实验是为了获得或解决某个数学概念、规律（法则、关系等）或问题，借助外在的物质工具和操作手段，进行数学探索的学习方式。数学实验将“做”“学”“思”合一，有效丰富与改进了数学学习方式，引导学生开展身心合一的具身认知，从而加深学生的数学理解。那么，小学数学教学中，教师应如何根据不同的教学内容，结合学生已有经验，积极开发和实施数学实验，有效深化学生的数学理解呢？

一、嵌入单项实验，聚焦知识理解

数学实验既可以是整节课的教学内容，也可以是一节数学课中某个环节或某一部分的内容。单项数学实验围绕一个知识点（例题、练习题、思考题等）的理解而开展，其教学时间可长可短，可以帮助学生理解数学问题的某一方面。因聚焦点小，所以频率高、易组织。这样的单项实验，直接指向对某个数学知识的理解与问题的求解。

（一）在结论验证时实验，加深意义理解

教学中，为了帮助学生理解新知，教师可将抽象的知识教学设计成直观的数学实验，让学生在动手操作中，带着问题去思考、去探究、去发现，从而深刻理解知识的重难点。

例如，苏教版小学数学六年级下册《圆锥的体积》一课教学，基于学生已掌握圆柱体积公式和圆锥特征的学情，教师先让学生大胆猜测：圆锥的体积可能与什么图形的体积有关？有着怎样的关系？验证猜想时，教师为学生提供等底、等高的圆柱和圆锥容器，让学生动手操作实验，在一次又一次的倒水过程中发现等底、等高的圆锥与圆柱的体积关系，从而得出圆锥的体积公式为V=13Sh。学生在数学实验中，将抽象的数学公式推导过程具体化，加深了对圆锥体积公式的理解。

计算教学中，在学生初步尝试计算得出结果或发现相关的运算规律、运算性质后，教师可以引导学生通过画图或实物操作实验，进一步加以验证，帮助学生深入理解算法和算理。

例如，蘇教版小学数学三年级上册《两位数乘一位数》一课教学，教师设计了“猜得数，说理由”的导入环节，让学生猜想21×3等于多少，教师根据回答追问：得数到底是61还是63呢？说说你是怎么想的？接着，教师组织学生开展验证结果的数学实验。学生通过摆小棒发现，21根小棒分成单根和整捆两部分，单根的是3×1=3，整捆的是3×20=60，合起来是63。形象的分小棒操作帮助学生轻松地理解了计算过程，得出了正确的计算法则。此时，教师及时引导学生回看61的答案错在哪里，进一步帮助学生深刻理解算理，熟练掌握算法。学生通过猜想、分析、实验、验证等过程的经历，不断加深对算理和算法的理解。

（二）在规律探索时实验，强化本质理解

在探索规律时，可以组织学生开展观察比较式数学实验，引导学生观察比较、思考判断、举例验证与归纳推理，从而强化对规律本质的理解。

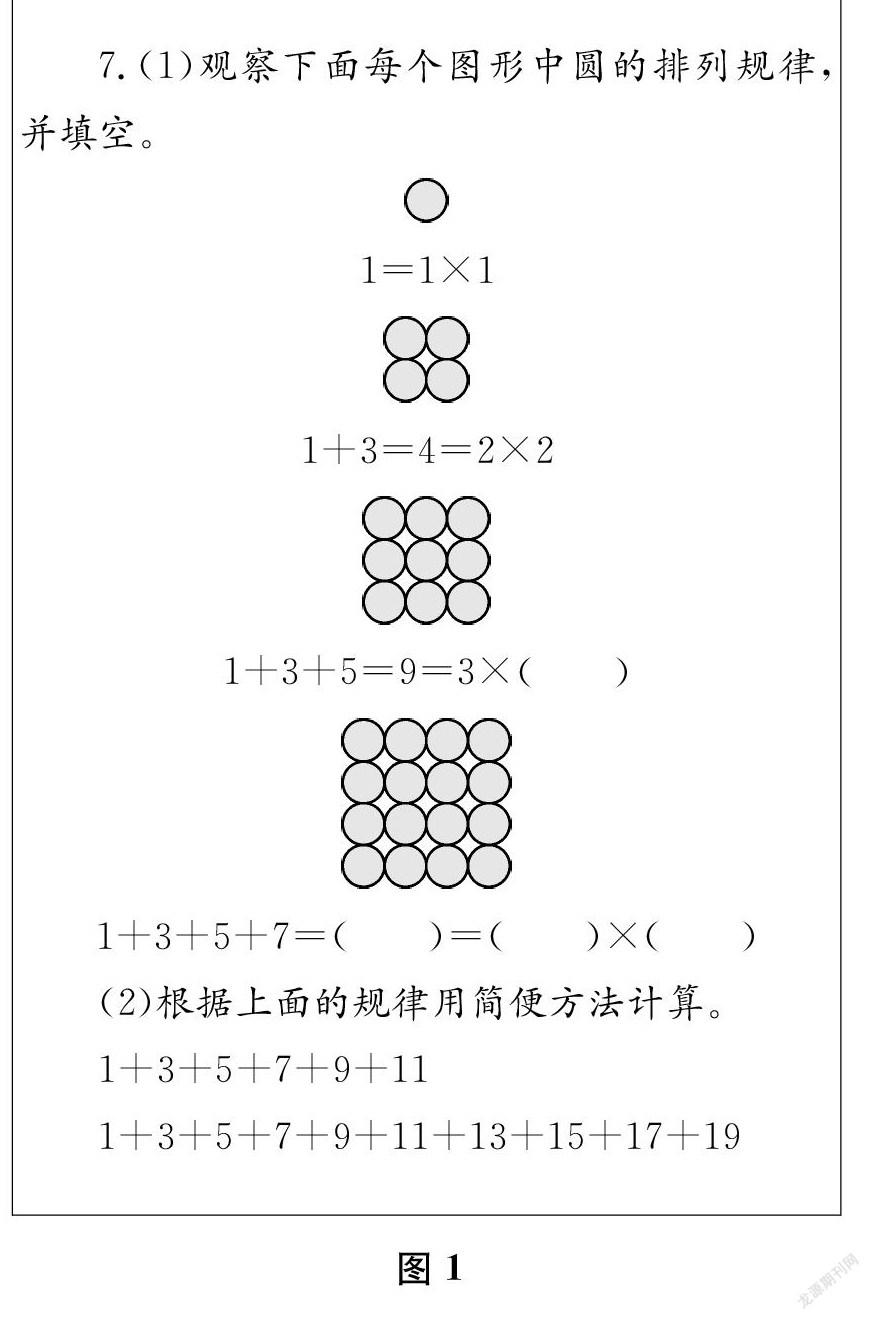
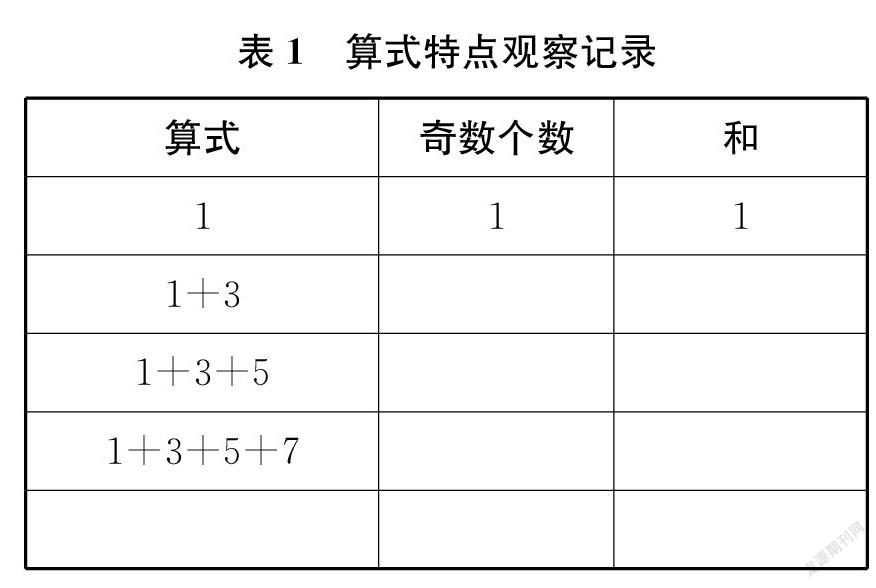
例如，对于苏教版小学数学五年级下册《解决问题的策略——转化》练习十六第7题（如图1），可以设计观察比较式数学实验：（1）算一算，比一比，你有什么发现？（2）想一想，写一写，还能写出这样的式子吗？任意写三个式子。（3）画一画，议一议，怎么会有这样的规律呢？在方格纸上画图，帮助观察比较、思考讨论。教师提供实验记录表（如下页表1），引导学生有序观察比较加数有什么特点，和有什么特点，加数与和之间有什么关系。这样的探索规律的数学实验中，数形结合，相得益彰，有效加深了学生对数学规律本质的理解。

二、开展组块实验，促进方法理解

小学数学教学中，还可以由若干连续数学实验组成组块实验。这类实验贯穿一堂课的始终，让学生以实验的活动方式，对相关内容进行整体认知及应用。组块数学实验一般有并联式和串联式两种实验方式，可以促进、加深学生对数学方法的理解。

（一）并联式组块实验，各个击破

并联式组块实验，顾名思义，由几个相同层级、不同侧重的数学实验构成，每一次实验都是在扩充学生对数学对象的认知。

例如，苏教版小学数学六年级上册《长、正方体展开图》一课，教师采用数学实验的方式教学：首先，省略按步骤剪、观察、认识展开图的过程，直接让学生在剪剪拼拼的实际操作中，思考如何才能得到展开图，让学生结合自身操作经验，在剪与拼的过程中发现正方体展开图的结构规律，从而根据规律分类归纳总结出展开图的不同类型;在此基础上，让学生迁移认识长方体的展开图。实验活动中，学生在以正方体展开图为目标的操作过程中，一边探索规律，一边也在深入理解概念及原理。由此，学生迁移经验认识长方形展开图，进一步加深对展开图的认识，并逐步发展空间观念。

（二）串联式数学实验，逐层深入

所谓串联式组块实验，由几个数学实验串联构成，每一次实验都是对前一次认知的深入，呈现认知的逐层递进。

例如，苏教版小学数学四年级下册《三角形的内角和》一课教学。课始，教师从学生已有的知识经验入手，将新旧知识联系起来创设现实情境，提出探索性问题——找、说三角板每个内角的度数，学生发现“三角形的内角和是180°”。接着，教师引导学生从特殊到一般展开猜想，借助已有的经验提出验证方法，让学生借助实验工具，动手、动口、动脑，对不同三角形的内角和进行操作验证。然后，教师引入几何画板软件，进行连续的变化验证，并进行适度的演绎证明，巧妙渗透数学方法，让学生经历发现、感悟、归纳、验证的过程。在串联式组块实验活动中，学生的分析逐步深化，思维不断丰满，对“三角形的内角和是180°”这一知识点以及“从特殊到一般”的探索方法的理解也不断加深。

三、实施融合实验，丰富经验理解

小学数学教学中，有时可以主题融合的方式，开展多角度、多内容、多学科的融合实验。主题融合实验递进式、阶段性地渗透、融合于较长时间的教学中，从课堂学习走向生活认知，方式多样、形式丰富、内容贴切，能有效增强学生具体可感的生活经历与体验，丰富学生对数学经验和生活经验的理解。

（一）多角度融合实验

教师可设计包含多个不同角度的数学实验活动，让学生充分动手、动口、动脑，多角度感知，帮助学生建立多元表象，加深理解。

例如，苏教版小学数学三年级上册《千克和克》一课教学，教师可引导学生在通过阅读了解质量单位，讲讲千克与克的生活小常识的基础上，感知1千克有多重，比比谁的“身体秤”更准……这一系列多角度的直观体验，能够帮助学生在头脑中建立“千克和克”的多元表象，丰富学生对“千克和克”的认识。

（二）多内容融合实验

针对教材上与学生现实生活联系紧密的内容，灵活整合学科内相关联的其他知识，组织学生利用实验材料，开展学科内多内容的主题融合实验，让学生经历数学实验的完整过程，进一步感受研究问题的科学方法，加深对知识和方法的理解。

例如，苏教版小学数学五年级下册《圆的认识》一课后，教师可以设计“车轮为什么是圆的”融合实验活动，引导学生结合认识的不同图形特征，开展观察比较实验，加深对圆的认识，积累对相關知识进行联结的经验。首先，教师通过问题“车轮为什么是圆的呢？做成正方形、长方形、三角形等其他图形可以吗？”帮助学生明确主题，有指向地开展小组讨论交流。教师巡视指导，帮助学生完成实验活动方案的制订。接着，学生分组开展实验活动，填写实验记录单。教师重点指导记录实验过程中不同形状车轮行驶轨迹的方法，引导学生体会不同车轮的轨迹，进一步理解圆的特点。最后，师生一起回顾实验过程，总结实验收获，帮助学生建立探索问题的模型，积累数学经验。

（三）多学科融合实验

有些数学实验的内容可以不局限于数学本学科知识，而整合多学科知识。教师可结合具体的实验内容，整合科学、美术、信息技术等学科资源（可请相关学科教师协同参与指导）。同时，此类实验可以由课内延伸至课外，由校内延伸至校外，拓展学习的场域，让学生在生活中学习，掌握学习的方法。

例如，苏教版小学数学六年级上册《百分数》一课，教师可创设“种子的发芽率”融合实验活动。课上，师生一起设计实验方案，厘清需要解决的问题以及数学实验方法等，培养学生科学研究的素养。在课后一周的观察实验中，学生小组合作，各司其职，持续观察、维护、拍摄、测量并记录发芽情况，最后计算、比较、汇总发芽率，科学地将数学统计与实验结果相结合进行分析。后期，学生根据实验过程资料积累，结合数学日记、制作PPT等进行成果展示与分享。整个实验过程，学生通过数据收集、整理、分析，进一步验证猜想与预测结果，不断反思调整，体会研究问题的一般过程与方法，提升实验素养，丰富眼界，加深对知识的理解。

参考文献：

[1] 匡金龙.利用数学实验，促进数学理解[J].教育研究与评论（小学教育教学），2020（5）.

[2] 潘小福，陈美华.小学数学实验教学的理论与实践[M].南京：江苏凤凰教育出版社，2019.

[3] 曹才翰，章建跃.数学教育心理学（第二版）[M].北京：北京师范大学出版社，2006.

[4] 王健.让数学实验从“纸面”真正走向“地面” [J].江苏教育，2017（9）.

3082500316520