反应堆控制棒驱动机构任务可靠性建模与分析
2021-03-16鲁文斌唐明堂吴泽豫王自力
李 维,邓 强,鲁文斌,唐明堂,吴泽豫,孙 博,王自力,任 羿
(1.中国核动力研究设计院核反应堆系统设计技术重点实验室,四川 成都 610041)(2.北京航空航天大学可靠性与系统工程学院, 北京 100191)
控制棒驱动机构(control rod drive mechanism, CRDM)是保障反应堆可靠性的关键部件。压水堆(pressurized water reactor, PWR)通过控制棒驱动机构带动控制棒组件运动,调整其插入堆芯的高度,从而对反应水平进行控制[1]。控制棒驱动机构属于小批量生产的特种装置,其生产成本较高,工艺结构较为复杂,工况环境较为恶劣[2];同时由于核电站反应堆停堆成本较高,使其具有较高的维修检测成本[3]。因此在产品设计阶段通过设计改进的方式使得控制棒驱动机构具有较高的固有可靠性水平,对于保障核电设备安全、高效、经济地运行具有至关重要的作用。
为了给产品设计改进提供支撑和参考,需要对产品的可靠性水平进行分析和评估[4]。对于控制棒驱动机构这种系统组成复杂、价格昂贵且工况特殊的产品,通常通过定性分析或建立仿真模型的方式对其可靠性进行分析[5-6]。但是,由于驱动机构系统组成复杂,难以直接对系统进行定性分析或建立全系统的仿真模型,一般需要建立系统任务可靠性模型分析其可靠性。建立系统任务可靠性模型的方法有建立任务可靠性框图模型(reliability block diagram,RBD)、故障树分析(fault tree analysis,FTA)模型、Petri网模型、Bayes网络模型等,以及基于这些基本模型的改进方法[7-10]。通过以上方法,虽然能够对动态系统建立任务可靠性模型并计算任务可靠度,却无法对存在跨时间片(time slice)关系节点的系统进行建模。对于控制棒驱动机构系统,其单步提升/下降功能均需要经过5个动作,由2组钩爪组件和3组衔铁线圈配合完成,其可靠性模型具有明显的跨时间片关系。
动态Bayes网络(dynamic Bayes network, DBN)是对一般Bayes网络的拓展,能够对随时间变化的随机变量以及它们之间的关系进行建模。近年来DBN在系统任务可靠性建模领域有了一定的应用[11-13]。其中,Wang等[14]对水下采油树系统不同维修状态下的可靠性进行了DBN建模,确定了系统的薄弱环节;Thanh等[15]提出了一种基于DBN的木质建筑结构可靠性实时评估方法。以上两项研究证明了DBN能够成功应用于存在跨时间片关系的动态、多态系统建模。
本文在总结以上研究的基础上,结合控制棒驱动机构产品特点,提出了一种基于DBN的控制棒驱动机构系统任务可靠性建模分析方法。以提升/下降功能为任务目标,通过Bayes网络对其提升/下降功能过程中不同步骤下不同单元的失效模式之间的关系进行建模,建立系统任务可靠性模型。随后利用所建立的模型对系统任务可靠度进行评估,并以典型控制棒驱动机构为案例对所提出的方法进行验证。
1 动态Bayes网络模型建立
1.1 Bayes网络建模理论
Bayes网络模型是一种可解释性强、支持静态和动态模型的建模方法。如图1所示,Bayes网络是一类有向无环图,如果从节点9到节点11有一条边,那么称9为11的父节点,而11为9的子节点。没有父节点的节点称为根节点,没有子节点的节点称为叶节点。在Bayes网络中,节点代表随机变量,节点间的有向边代表变量之间的直接依赖关系。每个节点都附有一个概率分布,根节点所附的是它的边缘概率分布,而其他节点所附的是它的条件概率分布,概率分布的表达形式可以是离散的分布表或连续的分布函数。建立Bayes网的过程一般包括建立节点、建立有向边和确定节点概率分布,通过建立Bayes网络,可以对其中任意节点的后验概率进行推理。
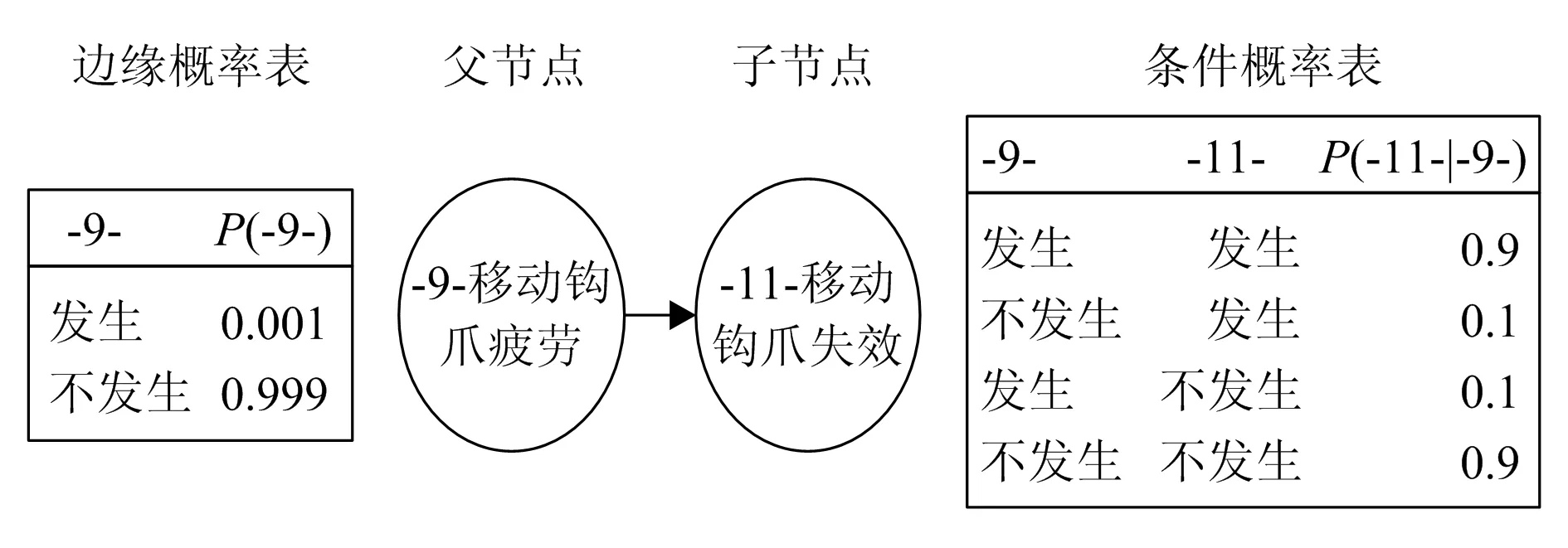
图1 Bayes网络基本组成
为了表达及推理随时间变化的随机变量,进一步引入DBN的概念。DBN是一个随着毗邻时间步骤把不同变量联系起来的Bayes网络,即具有多个“时间片(slice)”的贝叶斯网络。图2左图为一个具有4个时间片的DBN,包含2个节点:X和Y。对于每个时间片而言,X节点与Y节点之间有一条有向边,同时X节点与上一个时间片的X节点之间也有一条有向边,即上一个时间片的X节点的状态会对当前时间片X节点的状态产生影响。图2图左的DBN可以用图右的形式进行简化表达。

图2 动态Bayes网络示意
1.2 驱动机构动态Bayes网络建模流程
针对控制棒驱动机构建立DBN,首先需要通过功能原理分析明确其系统组成以及系统各单元之间的相互关系,进而确定关键失效模式和关联功能单元。随后根据驱动机构提升/下降功能的步骤对DBN的时间片进行划分,并根据功能单元失效模式间的传递关系建立节点和有向边,确定根节点的边缘概率和中间节点的条件概率。最后将不同的先验条件输入所建立的模型,对目标节点的概率进行推理。驱动机构DBN建模流程如图3所示。其中,最重要的两个环节分别为建立和确定动态节点以及建立有向边并确定节点的边缘/条件概率。

图3 驱动机构DBN建模流程
1)建立和确定动态节点。
步骤1,确定叶节点。对于可靠性Bayes网络模型,一般将系统功能完成作为叶节点以便于网络推理及输出结果。该节点一般包含两种可能的状态——“成功”和“失败”。
步骤2,确定根节点。一般将功能单元的失效模式、控制指令或环境事件等作为根节点。
步骤3,确定中间节点。中间节点表达了根节点(因)与叶节点(果)之间的关系,一般需要结合实际情况进行建立。通常可以根据产品对象的硬件结构和功能原理建立中间节点。
2)建立有向边并确定各节点的边缘/条件概率。
步骤1,建立静态节点相关的有向边。由失效模式确立的根节点与描述其单元失效的中间节点间应建立有向边;若某一单元的失效会导致其他单元失效,则应在这两个功能单元间建立有向边。
步骤2,建立动态节点相关的有向边。根据产品对象的功能原理,逐个时间片分析动态节点与其余节点之间的关系并建立有向边。
步骤3,确定节点的边缘/条件概率。网络中与失效模式相关的根节点的边缘概率值可以来源于零部件可靠性分析或仿真试验的结果,即失效模式发生概率;或者可以根据可靠性定性分析的结果对其边缘概率进行假设和估计。对中间节点和叶节点,其条件概率表值可以通过简单的条件概率计算或凭借工程经验进行假设估计。
1.3 Bayes网络模型推理计算
利用Bayes网络能够进行双向推理的特点,既可以从根节点推出叶节点的概率,也可由叶节点推断根节点的概率[16]。推理的基本算法为变量消元算法:
设X是一个Bayes网络Θ中所有变量的集合,Γ是Θ中所有概率分布的集合,按照Bayes网的定义,Γ是Θ所表示的联合概率分布P(X)的一个分解。假设观测到了证据E=e(其中E为观测到的变量集合(E∈X),e为E被观测到的状态),在Γ的因子中,将各证据变量设置为它们的观测值,得到一组函数,记为Γ′,这一步称为证据设置。不难看出Γ′是函数P(E=e)的一个分解,这里Y=XE(为集合的差运算)。
设Q是Y的一个子集,从Γ′中逐个消去在Y中但不在Q中的变量,得到另一个函数集合,记为Γ″,Γ″为P(Q,E=e)的一个分解。将Γ″中所有的因子相乘,就得到P(Q,E=e),由条件概率公式可进一步得到:
(1)

利用变量消元算法,输入根节点概率后可以推理得到叶节点的概率,其工程意义为在得知驱动机构功能单元的可靠度或失效发生概率后计算得到驱动机构系统的任务可靠度;反之,对于已知叶节点的发生概率后推理得到的根节点概率,其意义为该事件发生概率的上限值,即该功能单元失效发生概率在给定系统可靠性模型下的阈值。该阈值可以作为设计改进的约束。
2 案例验证
2.1 模型建立
我国引进的三代核电技术中使用的控制棒驱动机构的钩爪组件部分结构如图4所示[5]。其中由多组线圈、衔铁、磁极、钩爪及其连杆组成的机构实现驱动杆的提升和下降功能。

图4 控制棒驱动机构结构示意图
基于DBN建模方法建立的驱动机构提升功能的可靠性模型如图5所示。其中,动态部分框线以外的节点表达了驱动机构功能单元的失效模式传递关系,动态部分框线内的节点表达了提升程序的不同步骤中功能单元状态与组件提升状态以及是否发生意外落棒事件的关系;“结果”节点是Bayes网络的叶节点,其状态表达了提升功能的完成状态,作为输出节点。
假设驱动机构提升功能的DBN满足因果机制,同时其所有节点均取二值。则对静态节点“移动磁极失效”其条件概率见表1,对动态节点“完成提升/下降动作”其第3个时间片(t=2)确定的条件概率见表2,其余节点的条件概率从略。

表1 移动磁极失效条件概率表
2.2 模型计算与验证
以提升功能为例对本文所建立的DBN模型进行计算与验证。首先,将移动钩爪指令、提升/下降指令、保持钩爪指令等3个指令节点在不同时间片的状态作为证据输入模型,进而分别利用其不同运行步数下功能单元可靠度的数值计算其任务可靠度随提升步的变化。这里假设驱动机构除销轴之外的功能单元的可靠度均为0.999 999,销轴的失效发生概率仿真结果如图6所示,其中连杆-钩爪销轴的失效发生概率随着提升步的增加而显著提高。
将图6的结果代入DBN,计算得到驱动机构任务可靠度随提升步数的变化曲线,如图7所示。在第0.5E+07个提升步,驱动机构提升功能的可靠度为0.999 981;在第1.0E+07个提升步,驱动机构提升功能的可靠度下降为0.998 771。可见,随着钩爪销轴的失效发生概率的变化,驱动机构提升功能的可靠度随着提升步的增加而降低。假设驱动机构平均每年执行10 000个单步提升,则驱动机构预期寿命60 a对应的总提升步数为0.6E+07个,根据DBN计算结果,该提升步数的提升功能可靠度为0.999 979。

图5 驱动机构提升功能DBN可靠性模型

表2 无故障提升节点条件概率表(t=2)

图6 提升/保持钩爪的3类销轴失效发生概率曲线
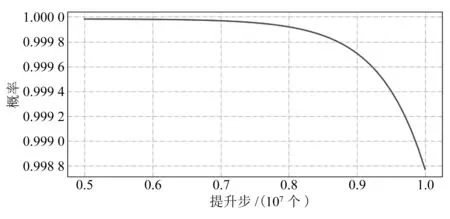
图7 驱动机构提升功能任务可靠度曲线
通过上面的分析可知,对于驱动机构的提升功能,当其功能单元(如销轴)的失效发生概率随着提升步数的增加而增加时,其任务可靠度随着总提升步数的增加而逐渐降低,在超过0.9E+07个提升步之后,可靠度的降低速率显著提升。按照60 a 0.6E+07个提升步数计,其60 a的任务可靠度为0.999 979,能够满足驱动机构的可靠度设计要求。
3 结束语
本文研究了基于动态Bayes网络对控制棒驱动机构提升/下降功能进行可靠性建模的方法,总结了建模流程。基于功能原理分析,建立了某型控制棒驱动机构提升功能的DBN模型,计算了驱动机构在不同提升步时的任务可靠度。其结果能够指导驱动机构系统的可靠性分析和驱动机构设计改进,有效提高系统的固有可靠性。本文提出的可靠性建模方法具有如下特点:1)该建模方法能够对驱动机构系统跨时间片的状态变化及其影响进行建模,为机构动态可靠性建模提供了新的思路;2)该建模方法能够计算驱动机构系统任务可靠度与功能单元失效发生概率之间的关系,能够利用功能单元的失效发生概率仿真结果预计系统整体任务可靠度;3)本文建立的DBN可靠性模型能够计算驱动机构系统/功能单元对应每一个动作步骤的可靠度/失效发生概率,对驱动机构运动状态的建模和描述较为精确,对设计改进具有较大的指导意义。
