基于交互正交试验法的喷嘴结构数值分析

尹凤福，刘 振，薛莲莲，张 超，刘振宇

(1.青岛科技大学机电工程学院，山东 青岛 266061)(2.海尔集团技术研发中心，山东 青岛 266101)

塑料分选系统的分离装置属于分选设备的执行机构，目前分选设备研究方向集中于识别装置和控制系统改进，而喷吹装置能耗高、喷吹不准确、噪声大等问题限制了分选设备的效率和精度。喷嘴是塑料分选过程中关键的部件，目标物被喷吹分离的动力来自于喷嘴喷射时的高速气体射流[1]。

喷嘴的用途多种多样，其形状、大小、通过的流体等都不尽相同，对其研究非常广泛。张福波等[2]利用计算流体力学软件Fluent对锥型喷嘴和柱形喷嘴的冲击换热过程进行了热流耦合模拟，模拟结果表明锥型喷嘴的射流冲击换热性能明显优于柱型喷嘴。罗静等[3]利用大涡模拟方法，对正弦曲线、双三次曲线、维多辛斯基曲线的收缩段的外部流场进行了数值模拟，通过对比分析得出正弦曲线喷嘴出口处的速度分布、湍流强度分布均优于另外两种曲线。梁博健等[4]结合正交试验法，对高压水除鳞喷嘴各结构参数及其交互作用对其性能影响的显著性及重要性次序进行分析，获得最优的参数组合并进行了实验验证。邓军等[5]利用计算流体动力学(CFD)软件对维多辛斯基曲线结构、锥直结构和锥角结构3种喷嘴结构进行选型优化，结果显示维多辛斯基曲线结构喷嘴的出口速度更稳定、集束性更好、能量转化率更高。苟湘等[6]利用宽频噪声源模型对喷管式汽水混合加热器进行气动噪声数值模拟，为改进汽水混合加热器的降噪研究提供参考。

本文采用数值模拟的方法对塑料近红外分选设备——喷嘴进行优化设计，为减少计算量，采用交互作用的正交试验法对其进行模拟计算。

1 数值模拟

1.1 几何模型构建

采用CAD软件建立喷嘴的几何模型，喷嘴的收缩段根据维多辛斯基曲线方程进行建模：

(1)

式中：r1为出口半径；r2为入口半径；l为收缩段长度；x为自收缩段入口开始的长度；r为对应x处喷嘴截面半径。

收缩段示意图如图1所示。为了降低数值计算量，采用二维计算模型对喷嘴的射流内外流场进行模拟，喷嘴的外流场指的是射流在大气中的作用范围，喷嘴的外流场的半径和长度分别为喷嘴出口半径的20倍和50倍。利用Gambit软件对几何模型划分网格，并根据实际情况设置边界条件，未标记的均为壁面(wall)，如图2所示。

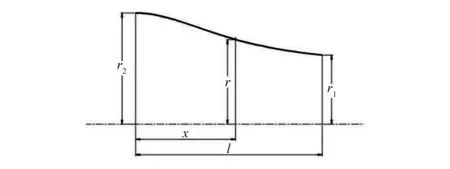
图1 收缩段结构示意图

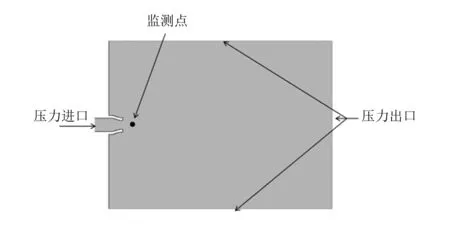
图2 网格模型

1.2 数学模型

求解过程选择基于压力(pressure based)求解器和稳态时间类型，采用realizek-ε湍流模型和宽频噪声模型(broadband noise sources)，利用二阶迎风格式的Simplec算法求解，其控制方程如下。

连续性方程：

(2)

动量方程：

(3)

(4)

能量方程：

(5)

式中：vx，vy分别为沿x，y方向的速度；ρ为流体密度；μ为流体的动力黏度；λ为热传导率；c为比热容；T为温度；g为重力加速度；t为时间。

噪声求解选择各项同性湍流噪声模型，即选择四极子噪声源[7]，计算公式如下：

(6)

式中：PA为四极子噪声源声功率；α为常量；h为气体密度；v为声速；b为湍流尺度；u为湍流速度。

1.3 求解模拟条件

本文以理想气体作为介质进行模拟，其他计算域条件见表1。

表1 计算域条件

喷嘴的出口半径、收缩比和收缩段长度对喷嘴射流性能影响较大，将这3个参数作为交互正交试验的因素，每个因素都选取3个水平，喷嘴结构参数因素水平表见表2。

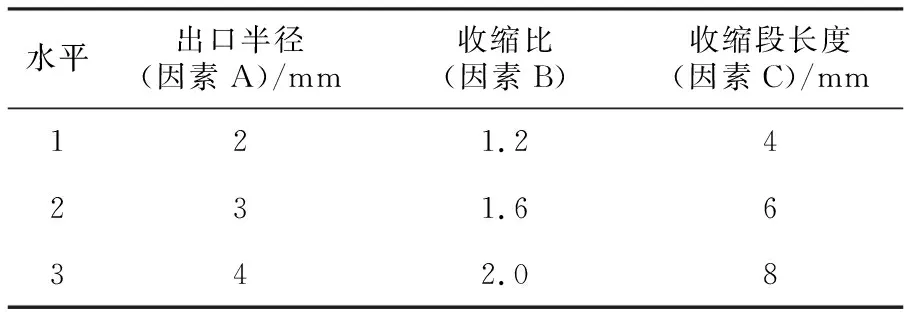
表2 喷嘴结构参数因素水平表

2 计算结果与分析

运用数值模拟并结合交互正交试验法，参考L27(313)正交试验表[8]，对试验中出口半径、收缩比和收缩段长度3个因素进行试验分布设计。其中，单因素 A，B，C分别置于第1，2，4列；交互作用A×B置于第3列，A×C置于第5列，B×C置于第6列；交互作用A×B×C置于第7列，并将其作为误差项，其他各列做空白处理。对交互正交试验表中各组数据进行仿真模拟，并设置如图2所示的噪声监测点进行监测。交互正交试验结果表见表3。

根据表3分析不同因素下极差与方差，通过对比反映出各因素对喷嘴指标模拟结果的影响。

2.1 极差分析

分析不同因素下极差R的大小，通过对比可以得出各因素对喷嘴指标模拟结果的影响，R值越大，该因素对应的指标影响越大。

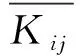
由表4可见，A的极差值最大，为29.5，B×C的极差值最小，为0.2，表明试验范围内，出口半径对射流核心段长度影响最大，收缩比与收缩段长度的交互作用对其影响最小。单因素对射流核心段的影响高于因素间交互作用的影响。各因素间的交互作用对射流核心段长度的影响由大到小依次为：A×B>A×C>B×C，即出口半径与收缩比的交互作用>出口半径与收缩段长度的交互作用>收缩比与收缩段长度的交互作用。

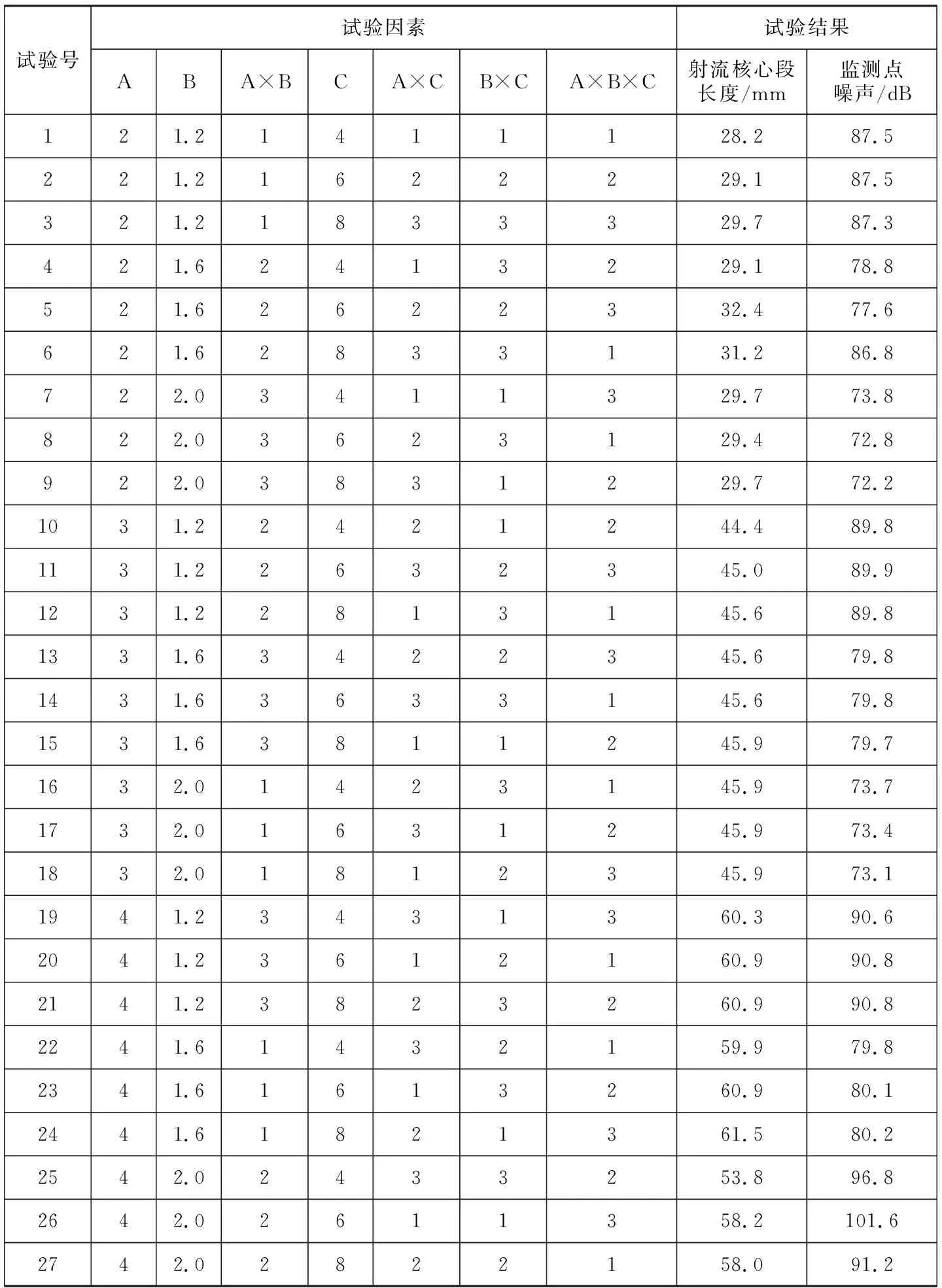
表3 交互正交试验结果表

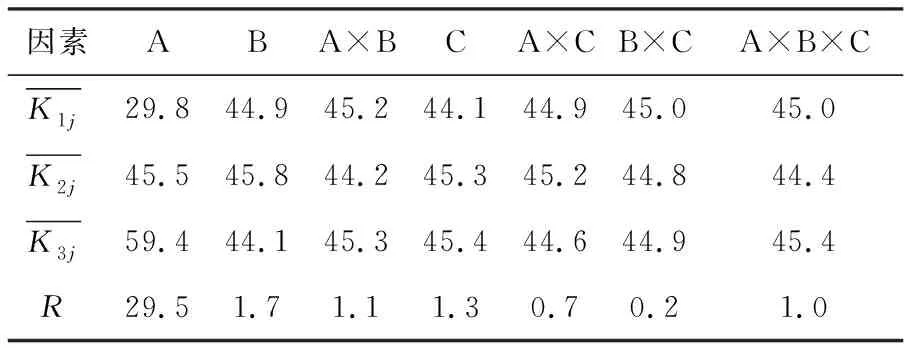
表4 射流核心段长度极差分析

由表5可见，A×B的极差值最大，为16.7，C的极差值最小，为7.9，表明试验范围内，出口半径与收缩比的交互作用对噪声影响最大，收缩段长度对其影响最小。各因素间的交互作用噪声的影响由大到小依次为：A×B>B×C>A×C，即出口半径与收缩比的交互作用>收缩比与收缩段长度的交互作用>出口半径与收缩段长度的交互作用。

表5 监测点噪声极差分析

2.2 方差分析

为了对各因素的影响程度进行定量分析，利用F检验对各因素及各因素间的交互作用进行方差分析。F检验计算公式如下：

Fα(n1,n2)=F

(7)

式中：Fα为F检验统计量函数，其中α为显著性水平；n1为各因素或因素之间的交互作用所对应的自由度；n2为误差自由度的总和。

若F>F0.05,则该因素具有显著性；若F>F0.01，则该因素具有高度的显著性；若F很小，并且S≤Se时(S为因素方差，Se为误差的方差)，则将这些因素的偏差平方和归入误差e的偏差平方和，其自由度归入误差自由度，使误差项增大，得到新的误差项eΔ，从而提高F检验的灵敏度。射流核心段长度方差分析结果见表6。

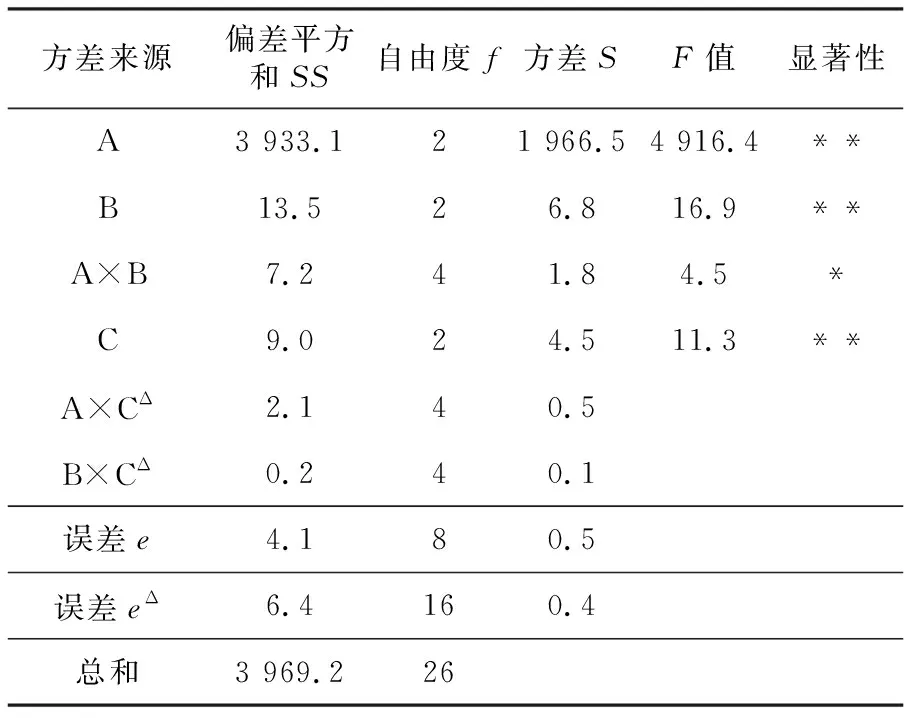
表6 射流核心段长度方差分析表

查F分布表，得F0.05(2,16)=3.63，F0.01(2,16)=6.23，F0.05(4,16)=3.01，F0.01(4,16)=4.77。由表6可知，A，B和C对射流核心段长度有高度显著影响；A×B对射流核心段长度有显著影响；A×C，B×C 对射流核心段长度基本无影响。由显著性分析可知，在试验范围内，各因素及因素间的相互作用对射流核心段长度的影响从大到小依次为：A>B>C>A×B>A×C>B×C，即出口半径>收缩比>收缩段长度>出口半径与收缩比的交互作用>出口半径与收缩段长度的交互作用>收缩比与收缩段长度的交互作用。射流核心段长度方差分析结果验证了极差分析结果。噪声方差分析见表7。

查F分布表，得F0.05(2,8)=4.46，F0.05(4,8)=3.84，F0.01(2,8)=8.65，F0.01(4,8)=7.01。由表7可知，A×B对噪声有高度显著影响；A，B，C，A×C和B×C 对噪声基本无影响。由显著性分析可知，在试验范围内，各因素及因素间的相互作用对噪声的影响从大到小依次为：A×B>B>A>C>B×C>A×C，即出口半径与收缩比的交互作用>收缩比>出口半径>收缩段长度>收缩比与收缩段长度的交互作用>出口半径与收缩段长度的交互作用。噪声方差分析结果验证了极差分析结果。

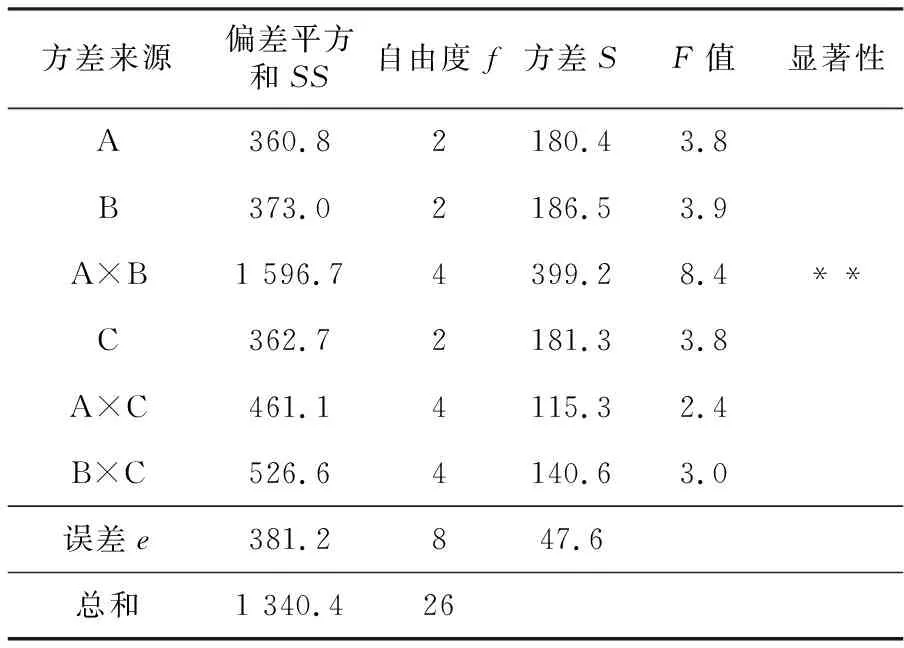
表7 噪声方差分析表

2.3 分析结果

通过交互正交试验法对喷嘴出口半径、收缩比和收缩段长度3个结构参数对喷嘴射流性能的影响进行分析，确定了最优的参数组合。当射流核心段长度这个性能指标最大时，各因素的水平分别为A3，B2，C3，(A×B)3，综合考虑A3×B2×C3为射流核心段长度最大的组合，喷嘴结构在选取的L27(313)正交试验表中存在，为正交试验表中射流核心段长度最大的组合，其大小为61.5 mm。当噪声这个性能指标最小时，各因素的水平分别为(A×B)1，B3，A2，C1，(B×C)2，(A×C)2。

综合分析，喷嘴的最优结构组合为A3×B2×C3，即出口半径4 mm，收缩比1.6，收缩段长度8 mm，此结构在选取的L27(313)正交试验表中存在，并且此组合模拟下的射流核心段长度为61.5 mm，监测点噪声值为80.2 dB。

3 结束语

本文利用交互正交试验法对喷嘴出口半径、收缩比和收缩段长度3个因素进行数值分析，结果显示这3个因素对喷嘴射流核心段长度、噪声均有显著影响。

对于喷嘴射流射流核心段长度，出口半径对其影响最大，出口半径增大，射流核心段长度增大。各因素对射流射流核心段长度的影响由大到小依次为：出口半径>收缩比>收缩段长度>出口半径与收缩比的交互作用>出口半径与收缩段长度的交互作用>收缩比与收缩段长度的交互作用。

各因素对噪声的影响由大到小依次为：出口半径与收缩比的交互作用>收缩比>出口半径>收缩段长度>收缩比与收缩段长度的交互作用>出口半径与收缩段长度的交互作用。收缩比越大，收缩段长度越长，噪声值越小。出口半径与收缩比的交互作用对喷嘴射流核心段长度及噪声均有较大的影响。