基于惯性基准法的轨道高低不平顺检测与预警系统

俞军燕，高一凡，王晨阳，邓桂棠，苏永生，李 懋

(1.广州地铁集团有限公司，广州 510330；2.北京锦鸿希电信息技术股份有限公司，北京 100070)

钢轨顶面在纵向的起伏变化称为轨道高低，它表明轨道在纵断面的不平顺情况.在钢轨长时间繁忙行车动载下，轨道高低质量的逐渐恶化产生的不平顺是引起机车车辆与轨道结构产生振动的主要激扰源[1]，会降低乘坐平稳质量和行车安全,影响旅客舒适度[2].因此，对轨道高低不平顺的检测，是全面提高线路质量，保障行车安全和平稳的基础[3]，关于如何有效检测轨道高低不平顺的问题，也早已成为国内外专家学者研究的重要课题.目前，对轨道高低的检测的方法主要有2种：弦测法和惯性基准法.

1)弦测法：弦测法通常需要2～3名工人共同完成[4]，常常采用平直尺或塞尺[5]，利用车体与多个车轮，在车辆上建立测量“基准线”进行的测量.其原理是：将检测车前后两轮与轨道接触点的连线作为测量的基准线，中间轮与轨道接触点偏离基准线的距离作为测量结果.传统弦测法以3点等弦法为主[6].

可用数学方法推导出弦测法的测量值与实际值之间的关系，通常把这种关系称为传递函数.以3点弦测法为例，其传递函数为：

(1)

式中：l代表弦长；λ表示轨道高低波长.

根据弦测法的计算公式，其传递函数不恒为1，随着轨道高低波长的变化，传递函数在[0,2]的范围内变化.因此，在弦测法中，当弦长保持不变时，高波长和低波长的测量增益是变化的，导致测量值在反映轨道高低不平顺的真实状况上精确性较差[7].为减小这种幅值增益误差，一般可使用多点弦测法，但这种因测量方法而产生的的误差并不会完全消除，所以，弦测法不能正确反映轨道的实际高低结果.

2)惯性基准法：惯性基准法是一种先进检测方法，它是利用惯性原理，获得测量基准[8].通过在轴箱上安装加速度计，采集振动加速度信号，然后对振动加速度信号进行二次积分，就可得到轨道的垂向变化值.

以W表示车体和轮轴之间的相对位移，通过位移计测出W，对a值进行二次积分后表示为Z，Z代表车体和惯性基准之间的相对位移，a值由加速度计A计算得出，计算高低不平顺的表达式为：

Y=Z-W-R

(2)

由式(2)可以看出，在惯性基准法中，传递函数保持为1，对于轨道的不平顺能进行相关检测，且通过公式计算，还能使结果以弦长准则来表示，同时，惯性基准法具有可测波长范围宽、对检测系统体积要求小的特点[9],且与弦测法的人工测量为主相比，惯性基准法能在一定程度上节省人力物力成本[10].因此，惯性基准法，在目前测量中得到了广泛的应用.

因此，本文针对弦测法存在的人工干预程度大、检测精准度低、反映不真实等缺点，利用惯性基准法的优势，结合新技术设计研发出一套用于轨道高低不平顺的检测与预警系统.

1 系统实现原理与特点

本系统通过惯组单元、激光视像组件和工控数据处理主机，建立惯性基准模型，使用激光视像技术和惯性测量技术对轨道高低进行动态检测.首先，设备启动后，工控数据处理主机通过向各采集设备同步硬件脉冲，对数据进行同步采集，并且将采集的数据进行滤波，带入各参数指标的数学模型中，利用求解差分方程的方式，得到轨道高低；然后，通过列车速度信息以及数据的采样时间，将“等时”数据转换成“等距”数据；接着，根据轨道高低的历史数据，将轨道高低不平顺随时间的变化分为3个阶段，即磨合期、正常磨损期和加剧磨损期；最后，进行分段拟合，得到轨道高低不平顺的趋势曲线，与轨道高低阀值进行对比，完成对轨道高低不平顺的预警功能.系统特点如下：

1)采用惯性基准法测量轨道高低，精度高，抗干扰能力强；

2)整个系统安装在运营列车上，通过列车运行，自动完成对全线轨道波磨的监测，检测范围广；

3)结合历史数据，绘制关键部位的轨道高低趋势曲线，进行趋势预测和报警；

4)使用惯组单元进行测量，集成度高，安装简单，易于维护；

5)算法工程实现简单、快捷.

2 系统架构组成与单元功能

2.1 架构组成

轨道高低不平顺检测与预警系统由工控数据处理主机、惯组单元、高低加速度传感器、激光视像组件、光电编码器组成.列车上电后，工控数据处理主机发出硬件同步脉冲给采集设备，开始进行数据的同步采集.工控数据处理主机根据光电编码器采集的转速信息，结合采样时间，将“等时”轨道高低数据转换为“等距”轨道高低数据；最后，结合轨道高低的历史数据，采用多项式拟合的方式，绘制出轨道高低随时间变化的趋势曲线，从而完成对轨道高低趋势预测的功能.系统组成结构如图1所示，系统主要结构参数如表1所示检测系统实现如图2所示.

图1 检测系统组成结构示意图

表1 各结构名称与用途

图2 检测系统实现流程示意图

2.2 设备原理

2.2.1 惯组单元IMU

惯组单元是可靠的固态惯性测量单元.内置三轴硅陀螺仪、三轴硅加速度计和 GPS 接收机，为达到各种工况下的使用要求，还要经过三轴转台的精细化调整，并依靠内置DSP结合卡尔曼滤波器展开数据融合，确保能提供瞬态、精准的组件状态和测量数据.

惯组单元精确校准陀螺仪的零点、零点温度系数、灵敏度、灵敏度温度系数、正交性误差和加速度效应.加速度计的零点、零点温度系数、灵敏度、灵敏度温度系数和正交性误差，不同波特率，不同模式下允许的最高数据速率不相同.使用该惯组单元，省去了对模拟二阶低通滤波、纠偏滤波、数字补偿滤波的过程，直接使用惯组单元的输出值，求解差分方程，完成计算.

2.2.2 高低加速度计

根据惯性基准原理，车体相对惯性基准的位Z，是由二次积分表示，该二次积分来源于高低加速度计的输出响应；即：Z=∬a(t)dtdt.高低加速度计以数字量输出，完成了模拟滤波、纠偏滤波、数字补偿滤波的滤波过程.

2.2.3 激光摄像组件

激光摄像组件由2个2D激光传感器组成，分别安装在左右钢轨的正上方，主要完成轨廓坐标数据的采集及左右轨顶距离信息.2D激光视像传感器都安装在特殊设计的检测梁上.

摄像结构主要完成的功能是：①寻找明亮条带.整个视频只有几个区间是需要明亮条带的.如以提升速度为目的，应采取特征法，辨别明亮条带的自身特征，确定明亮条带边缘轮廓，以加窗法覆盖其上，在后续中只针对加窗部分进行处理.②处理视频图像.过滤高频信号，以中值法过滤噪声，调节图像灰度值，利用直方图调整对比度，灰度二值法，区间隔断等.③加深处理明亮条带.确定明亮条带的中心位置.可采用不同办法：一种是以细线算法处理灰度二值图像，以细线处理、剪枝、间隔等；另一种是对整个图片灰度化后，再以细化算法进行处理.④平移转换坐标位置.这一处理方法在于定位和修正图像.⑤确立系统参数.在对明亮条带进行加深处理和平移转换坐标位置时，需要明确很多参数，在实际中为保证参数值不出现波动，应以一装置作为基础，将光源、摄像机等部件牢牢固定其上，在一定程度上保证其位置不出现变动，并确保光照面与轨道纵向轴始终成90°.

2.3 算法原理

2.3.1 数学模型

根据惯性器件的安装组合形式，以转向架承载检测梁，检测梁承载传感器为基础，构建轨道检测数学模型.

图3中1为惯组单元；2为左高低加速度计；3为右高低加速度计；4为左激光视像组件；5为右激光视像组件；6为光电编码器.G表示左右钢轨顶面中点之间的距离，为常值；ht表示惯组单元安装点到轨距测量线的距离.

图3 传感器安装示意图

2.3.2 等时变等距

根据要求的等距数据间隔(例如：0.25 m 1份数据)，将已经求出的[时间-高低]序列 转换成为[位移-高低]序列.具体方法是，根据[时间-车速]序列，将当前车速×时间间隔，先转换成为非等距的[位移-高低]序列，在通过线性插值法，得到等距的[位移-高低]数据.图4为变换结果示意图.

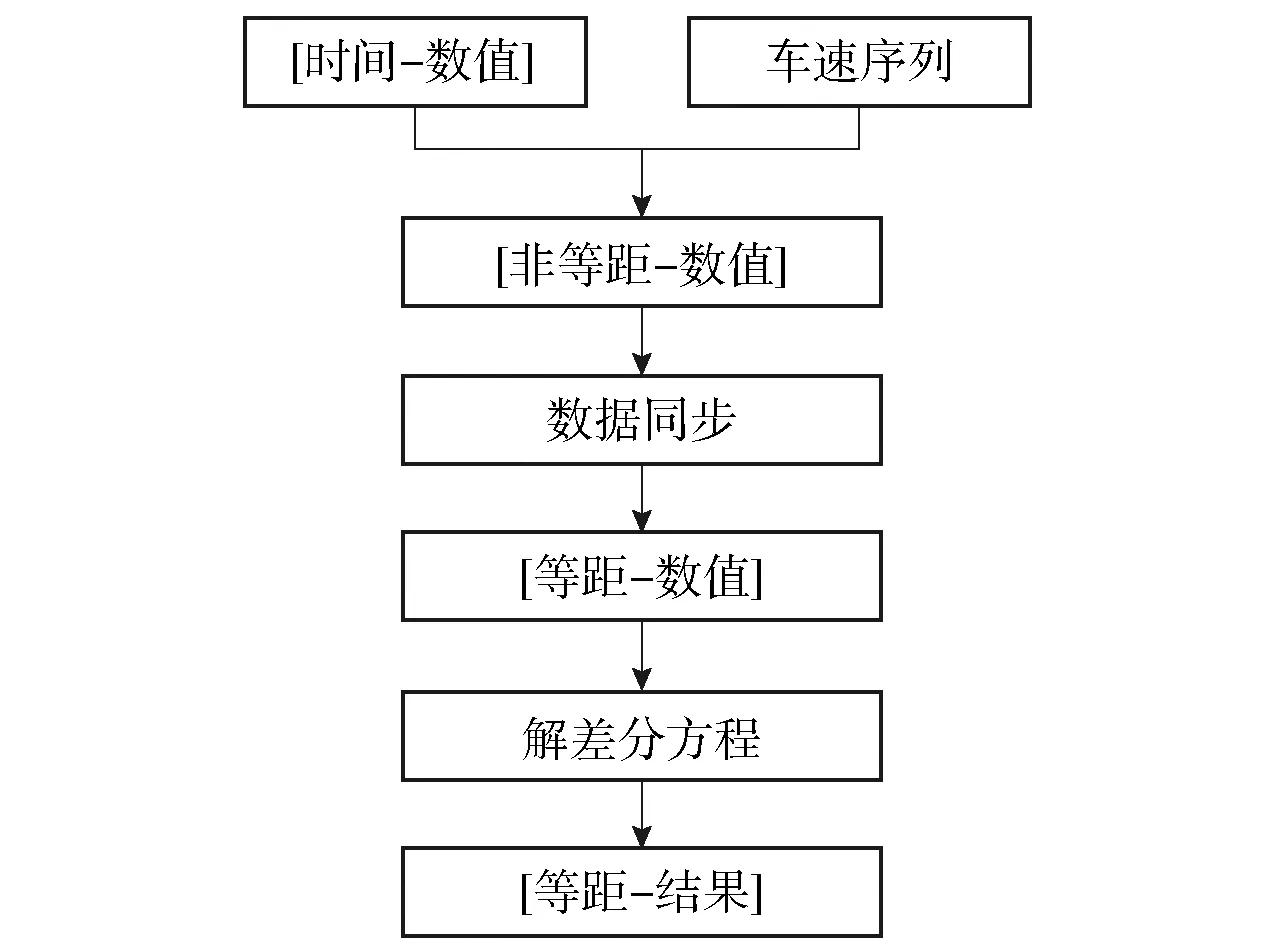
图4 等时变等距示意图

在使用线性插值将“等时”数据转换为“等距”数据时，对于单调性变化较大的序列，容易产生数据失真的现象.例如：高低加速度，可能会像一次函数这样的波动数据，在数采集的过程中，丢失了中间方框内的部分.图5为数据丢失示意图.

图5 数据丢失示意图

使用线性插值法时，绘出的图像如图6所示.

图6 线性插值法图像示意

很显然，重采样的数据与数据丢失期间的真实振动数据不匹配.为了涵盖这种情形，可引进这样一个参数，用来表示为了能插值，设置数据缺失的间隔最大值.如果间隙大于这个指定的最大值(例如1 ms)，数据点不会被插值，而是返回一个 NaN(Not a Number)值代替.

2.3.3 关键平面及夹角

在理论推导的过程中，还需要明确水平面、检测梁平面、轨道平面之间的相互关系.如图7所示.

图7 平面关系示意图

图7中惯组单元y轴所在平面是检测梁平面，轨道几何尺寸测量的平面是轨道平面，惯组单元的参考平面是水平面.θb为检测梁倾角(检测梁平面与水平面之间的夹角)，由惯组单元测量得到，θb分为高频成分θbh和低频成分θbl，即θb=θbh+θbl；其中θbh由惯组单元的输出值滚动角速度ωx在高通滤波的基础上一次积分获取；θbl由惯组单元的输出值摇头角速度ωz以及y轴方向上的加速度αy计算得到.

检测梁平面同水平面夹角的测量流程示意图如图8所示.

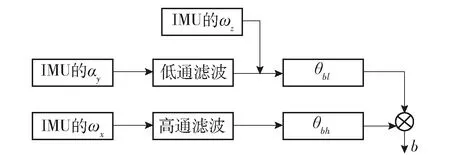
图8 测量流程示意图

θbt为轨道平面与检测梁平面之间夹角，见式(3)：

(3)

式中：δR为右激光摄像组件到轨顶面的距离，由右激光摄像组件直接测量得到；δL为左激光摄像组件到轨顶面的距离，由左激光摄像组件直接测量得到；G为左右钢轨顶面中点之间的距离，常值为1 500 mm.θt为轨道平面与水平面之间的夹角，θt=θb-θbt.

2.3.4 轨道高低的计算

轨道高低的计算包括两部分：①高低加速度计、水平、曲率响应系统的补偿；②激光摄像组件、测量车体、架构、轨道相对位置变化.

轨道左右高低HL和HR分别为：

(4)

式中：Z′L代表静态标定时，左高低加速度计到左轨轨顶面的距离，为常值；Z′R代表静态标定时，右高低加速度计到右轨轨顶面的距离，为常值；ZL代表左高低加速度计偏离左轨轨顶面的垂向变化，由左高低加速度计和激光摄像组件测得；ZR代表右高低加速度计偏离右轨轨顶面的垂向变化，由右高低加速度计和激光摄像组件测得；θt代表轨道平面与水平面之间的夹角，由倾角仪和激光摄像组件测得.

因此，求HL和HR的计算转化成为求ZL和ZR的计算，见式(5)：

(5)

式中：ZCL为左侧高低加速度计中心偏离检测梁平面的垂向距离；ZCR为右侧高低加速度计中心偏离检测梁平面的垂向距离；δL为左激光摄像组件到轨顶面的距离，由左激光摄像组件直接测量得到；δR为右激光摄像组件到轨顶面的距离，由右激光摄像组件直接测量得到；θb为检测梁倾角(检测梁平面与水平面之间的夹角)，由倾角仪和惯组单元测量得到.

因此，求ZL和ZR的计算转化成为求ZCL和ZCR的计算.因为，安装在检测梁上的左右高低加速度计的响应为：

(6)

所以可得到：

(7)

由于式中的信号均是时域中的连续信号，需要通过信号处理(重采样，滤波)，其基本思想是把微分方程化为差分方程，又由于三角窗函数比较适用于分析有较强干扰噪声的窄带信号，因此，选取三角窗函数g(t)作为求解微分方程的窗函数.求解二阶微分方程，将上述公式两边同时对三角窗函数g(t)卷积得到：

(8)

(9)

由此，得到ZCL和ZCR，从而获得ZL和ZR，以及左右高低HL和HR.

2.3.5 曲线拟合与趋势预测

轨道高低不平顺一般根据钢轨投入使用的运营时间分为磨合期、正常磨损期和加剧磨损期.为正确表征轨道高低随时间的变化趋势，需要根据轨道检修日报，记录钢轨的运营时间，并进行分段拟合，将轨道高低趋势曲线分为3段，首先对得到的历史数据点坐标(xi,yi),i=1,2,…,n，分为3组，x表示时间，y表示高低值，即：

(10)

式中：N1,N2,N3表示每个区间数据点的个数，则有：

N1+N2+N3=n

(11)

数据分布在各个区间上，且由于在某个限度内，以多项式能表示不同定义域的连续函数，因此明确拟合方程F(x)在M个数集上的多项式可设为：

(12)

式中：不确定系数以α表示；线性无关的基函数{1,x,x2,…,xn}以f(x)表示；该区域内基函数数量以m1，m2,m3表示.根据钢轨在不同时期钢轨磨耗随时间的变化，将磨合期设置二次函数形式，正常磨损期设置为一次函数形式，加剧磨损期设置为指数函数形式.

以最小二乘法为基础，进行曲线拟合，最小二乘法估量以S表示，可使拟合误差降至最低，且在断点处导数达到三阶的表达式为：

(13)

为保证曲线在各分段点xom处，Fm-1(x)过渡到Fm(x)时曲线连续，则要保证位于xom时，前段曲线和后段曲线的值一样大，因此要加入约束条件用以限制其值：

Fm-1(xom)=Fm(xom)

(14)

同时，为了保证曲线在xom处，Fm-1(x)过渡到Fm(x)时曲线平滑，并保证曲线拟合后，其能用于几何分析，因此要保证位于xom时，前段曲线和后段曲线具有连续的三阶导数，也要加入相应的约束条件：

(15)

根据以上内容即可求出未知系数，然后计算拐点，并以拐点为起止点进一步平滑曲线，最终获得轨道高低不平顺的趋势曲线如图9所示.

图9 轨道高低不平顺趋势曲线

最后，结合轨道高低的阀值，与当前得到的轨道高低不平顺的趋势曲线对比，计算得到轨道高低超限时间，及时通知检修人员更换钢轨.

3 结论

本系统利用惯性基准法，通过在轨检梁上构建惯性基准模型，利用轨道高低加速度计、惯组单元、激光视像组件配合完成轨道高低不平顺的检测.利用光电编码器采集车轴转速，进而计算得到列车位移，使用线性插值法，将等时轨道高低数据转换成等距轨道高低数据.最后，根据同位置下不同时间的轨道高低不平顺的测量值，将轨道高低的变化分为3个时期，分段拟合轨道高低趋势曲线，再与轨道高低的阀值进行对比，得到轨道高低不平顺的检测结果和超限时间，完成对轨道高低不平顺的预警功能.