用张量分析方法推导含偶应力弹性力学有限元理论

孙晓勇，宋兴海，侯娜娜，付建航，刘立悦

(1.河北省数据中心相变热管理技术创新中心，河北省沧州市重庆路1号 061001；2.河北水利电力学院 土木工程学院，河北省沧州市重庆路1号 061001)

1 经典线弹性理论与考虑偶应力线弹性理论

在经典弹塑性力学理论中，物体内任意一点的应力状态只和应变或应变的历史有关，其基本变量为位移，对位移求梯度得到应变张量，用位移梯度描述无限小的变形，然后再由一点的应变张量分析得到应力张量[1]。含偶应力的线弹性力学理论认为，物体内任意一点的微元体，除有各个方向的位移外，还有本身的旋转变形，而这种旋转变形并非单纯的以旋转角表达，而是用和应变张量一个量级的旋转张量来表示[2]。经典弹性力学理论中微元体也有旋转，其将旋转视作微小的体积单元的刚体转动，即只有旋转位移，没有旋转变形。这样处理将带来其他问题：如果以刚体微小旋转表示单元体旋转，那么相邻的两个微元体将会控制不同的微小旋转，从而无法满足旋转自由度的连续性。对位移求梯度，会得到9个不同的分量，而在经典弹性力学理论中，由位移求梯度得到的应变张量却只有6个独立的分量，剩下的3个分量去哪里了？含偶应力的弹性理论认为，另外的3个分量应由旋转张量提供[3]。含偶应力弹性理论中，基本变量仍然是位移，对位移求梯度，将位移梯度分解为应变张量与旋转张量之和，其中应变张量是对称张量，而旋转张量是反对称张量[4]。旋转张量与旋转矢量一一对应，对旋转矢量求梯度得到曲率张量，用曲率张量表示微元体的旋转变形[5]。很显然，曲率张量比应变张量低一个量级。这就解决了相邻单元旋转自由度不连续的矛盾，因为相邻微元体的旋转矢量是连续的，所以用旋转矢量或旋转张量表示的旋转自由度也是连续的。因此，含偶应力弹性理论是经典弹性理论的一个补充，微元体变形不再只有平动变形，增加了旋转变形，平动变形以应变张量来表示，而旋转变形以曲率张量来表示。含偶应力弹性理论中增加了偶应力与曲率张量的本构关系，引入了旋转模量作为材料的基本参数[6]。因为偶应力相对于应力小一个量级，因此在宏观尺寸下，经典弹性理论不考虑偶应力不会影响到结果的精确性，而在微尺度下，偶应力所占比重增加，不考虑偶应力将带来结果上的很大误差，这也就是为什么微尺度受力构件会有尺寸效应的原因。

2 含偶应力线弹性理论

含偶应力弹性理论有悠久的发展历史。早在1887年，Voigt[7]就提出，将物体分解为很多个体积接近于零但不为零的微小单元，微小单元上作用有体力偶和面力偶，相邻的微小单元接触面上的力偶连续。1909年，Cosserat兄弟[8]提出了Cosserat理论，他们把物体分解成刚体颗粒，每个颗粒可以平移还可以转动。物体的变形就以每个颗粒的平移和转动来表示。在1960年后，Toupin[9]，Mindlin和Tiersten[10,11]，Koiter[12]等建立了较完善的偶应力理论[13]，在Cosserat理论基础上，他们认为，微元体的变形仍由平移和转动组成，但表示转动的矢量是由位移矢量得到的，相互不独立。2002年，Yang[14]在Mindlin基础上，又对偶应力理论进行了改进，从应变能的角度，建立了由应变张量和旋转矢量梯度共同组成的应变能密度表达式。Yang的理论简化了偶应力理论的本构关系，将材料参数定为3个，除传统的杨氏模量和泊松比外，增加了一个内禀特征尺寸参量，用以表示旋转变形本构关系，即后来的旋转模量。

2.1 含偶应力弹性力学理论有限元推导

2.1.1 基于偶应力理论的几何描述

对位移求梯度，可以表示材料内部的无限小变形，得到非对称的二阶张量，可以分解为2部分：

uij=εij+Ωij

其中，应变张量ε和旋转张量Ω与位移的关系分别为

旋转矢量ω与旋转张量Ω一一对应，关系式为

Ωij=-ωij∶εijk

其中，ε是置换张量。写为矩阵形式：

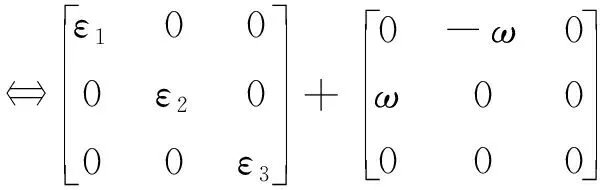
旋转张量Ωij是斜对称张量，其物理意义为微元体体积不变时的旋转变形。引入曲率张量χij表示材料中任一点转动变形的程度：

χij=ωji

曲率张量由旋转矢量求梯度得到，而旋转矢量又是位移旋度的一半，可以得到曲率张量和位移矢量的关系表达式：

而曲率张量的迹为零，即trχ=0。

根据ε∶Ω=0，可知应变张量εij和旋转张量Ωij相互独立。平动变形和转动变形以图形表示，如图1所示。

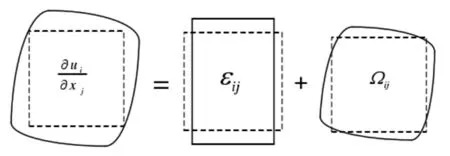
图1 无穷小变形分解为平动变形和转动变形Fig.1 Infinitesimal deformation is decomposed into translational deformation and rotational deformation

2.1.2 基于偶应力理论的Hamilton原理

动量矩定理：

动能定理：

式中：x为微元体位置，υ为速度，U为单位质量机械能。

建立虚功原理方程：

在含偶应力弹性理论中，位移是惟一的独立变量，旋转角根据位移求得。但是在进行有限元分析时，将节点位移视作未知量可能会引起节点旋转角的不连续。为了避免因未知旋转角引起的需要建立C1连续高阶元，增加虚功原理的约束条件，引入罚函数项：

式中：φi是未知的旋转角，α是罚函数因子。

把弹性体离散为六面体单元，每个单元有8个节点，每个节点有6个自由度。将单元内任一点位移写成矩阵列向量形式：

每个节点的位移也写成矩阵列向量形式：

di=[uixuiyuizφixφiyφiz]T(i=1～8)

将单元内任一点位移离散：

其中，矩阵[Ni]=NiI6×6，形函数

应变表示为矩阵的形式：

其中

ε=[εxxεyyεzzεxyεyzεxz]

χ=[χxxχyyχzzχxyχyzχxzχyxχzyχzx]

因此，应变矩阵由节点位移矩阵表示为

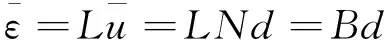
其中

B=LN=[B1B2…B8]

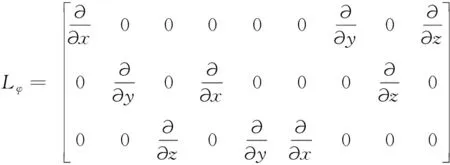
其中

Bα=[Bα1Bα2Bα3Bα4Bα5Bα6Bα7Bα8]3×48

且

2.1.3 基于偶应力理论的本构关系

含偶应力理论中应力表示为

其中

σ=[mxxmyymzzmxymyzmxzmyxmzymzx]

同样，应变表示为

其中

ε=[εxxεyyεzzεxyεyzεxz]

χ=[χxxχyyχzzχxyχyzχxzχyxχzyχzx]

由本构关系σij=2μεij+λθI和mij=4ηχij得：

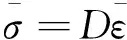
其中

Dφ=4ηI9×9

2.1.4 基于偶应力理论的有限元求解格式

其中

对坐标进行等参变换：

其中

将Ni对局部坐标求导得：

其中，雅阁比矩阵J可改写为

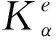
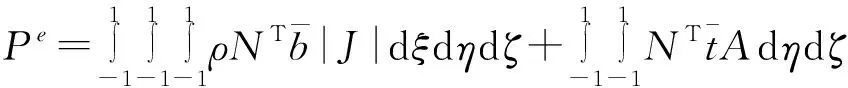
2.1.5 平面问题有限元求解格式

对于平面问题，将六面体单元简化为四边形单元，每个单元的4个节点上均存在3个自由度。

其中形函数矩阵：

[Ni]=NiI3×3

而

平面问题应变矩阵：

应变由节点位移表示：

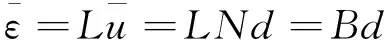
其中

B=LN=LNd=[B1B2B3B4]

Bi=LNi

根据

所以有

即

Bα=[Bα1Bα2Bα3Bα4]

其中

平面问题应力列矩阵为

平面问题应力与应变矩阵关系为

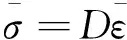
其中

Dφ=4ηI2×2

平面问题的体力表示为

面力表示为

于是，单元有限元控制方程可写为

经等参变换，其中质量矩阵、刚度矩阵、罚函数矩阵和外力矩阵分别可表示为

3 结束语

含偶应力弹性理论是经典弹性理论的进一步发展。文中从几何描述、能量原理、本构方程等方面阐述了考虑偶应力对弹性力学理论产生的影响；按照以位移为基本变量，旋转变形由位移导出，总应变分解为对称和反对称部分，对称部分代表经典弹性理论中的应变，即平动变形，反对称部分代表旋转变形，对虚功原理方程增加了罚函数因子，从而引入约束条件，避免了需要构造C1连续单元求解未知旋转角带来的高阶元求解的困难。运用等参元离散有限元方程，对三维及二维问题的有限元求解过程进行了详细推导，其结果可用于计算平板上偶应力分布及旋转变形分布等问题，对三维及二维问题中结构变形、裂纹的产生以及材料的破坏等均可进行力学评价。