关于一类抛物问题爆破时间下界估计的注记

王园园,霍志鑫,孔德志,程树明,周利杰

(1.河北水利电力学院 基础部，河北省沧州市重庆路1号 061001；2.河北水利电力学院 电气工程学院，河北省沧州市重庆路1号 061001)

文中，将估计如下问题确定爆破时间的下界

(1)

其中，Ω⊂n(n≥3)是光滑的有界域，表示u边界上的外法向量，u0(x)是一个连续的非负函数。

函数f(t,s)和G(s)满足2个假设：假设(f)和假设(G)。

假设(f)：

(f1)当s≥0时，对任意的x∈Ω,t>0有f(t,s)≥0；

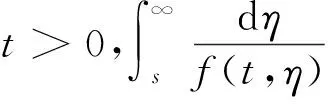
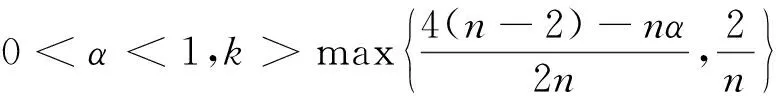
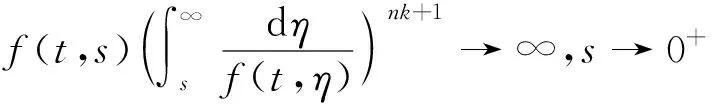
假设(G)：

(G1)当s≥0时，G(s)≥0并且G′(s)≥0；

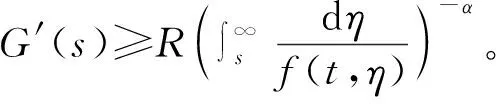
关于拟抛物型方程解的爆破条件以及爆破时间上下界估计，近年来国内外有很多学者在研究[1-13]，而本注记将采用[13]的思想方法并利用一些不等式估计，将文[13]中的结果推广到含散度型微分算子以及非线性项形式更一般的情形。

为了估计问题(1)爆破时间的下界，与文[13]类似，可定义

(2)

因为本文中只是关心爆破解，所以假设

(3)

直接计算可得

根据前面的假设(f)和(G)，可以推出：

因此

(4)

记C(Ω)是如下Sobolev不等式中的最佳常数

(5)

接着，运用Hölder不等式、含ε的Young不等式以及一般的Sobolev不等式，可得

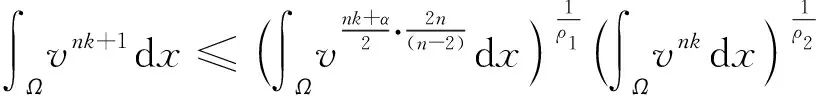
(6)

这里的ε待定，其中

(7)

(8)

因为0<α<1，运用Young不等式可以得到

(9)

将式(9)代入式(8)，可以得到

(10)

(11)

对式(11)从0到T积分，可以得到

(12)

其中

(13)

(14)

(15)

将上述结果写成如下定理的形式。

定理：设u是式(1)的爆破解，且f和G分别满足条件(f)和(G)，则爆破时间的一个下界可用式(12)来进行估计。