高速移动通信的信号优化方案研究

戴芬良

（贵州工业职业技术学院，贵州 贵阳 550008）

0 引 言

1 高速移动通信原理及传统算法的不足

高速移动通信是利用信息采集设备获取高速移动通信期间产生的信号，从中随机抽取一组样本作为通信节点，以节点位置和权值作为调节对象，使得生成样本与实际信号更为贴合[4]。计算样本均值，将计算结果记为信号传输状态的估计值。在此基础上，重新采集样本，此时得到的信号传输状态更为精准[5]。假设高速移动通信作业中的信号传输模型为：

式中，vk代表干扰信号，h(·)代表非线性函数，φk+1代表干扰信号，f(·)代表非线性函数，xk+1和zk代表协方差。

为了实时获取高速移动通信期间信号的变化情况，对当前信号状态采取更新处理，相关的公式为：

式中，η(xk|Zk-1)和η(xk|Zk)均代表概率密度函数。

考虑到运算量较大，为了高效准确计算结果，向模型中添加概率密度函数，通过抽样获取信号样本数据，而后运用信号状态模型递推样本信号，计算公式为：

式中，xik代表信号样本，φtk代表通信信号，η(xik|xik-1)代表节点，η(zk|xik)代表参数为xik的概率密度函数，θ(xik|xik-1,Zk) 代表通信函数，φtk-1代表信号权值。

在此期间，要求信号权值方差达到最小。为了满足此要求，设置节点θ(Xk|Zk)作为通信信号样本，采用随机选取方式，从中获取一部分节点。为了得到信号状态变化情况，更新各个节点权值[6]。该操作实际上就是多次调整信号干扰状态，以此达到改善高速移动通信质量的目的。

以上介绍这种通信方法中节点数目固定不变，如果外界环境发生改变，那么节点运算量就会随之增加，导致计算条件变得复杂，加大了计算难度[7]。节点数目与计算条件复杂程度之间的关系为o(N)∞N(节点数目)。

(1)各级党委要认识到位，坚持把关心下一代工作作为一项战略任务，纳入学校和院系日常管理工作，站在确保党和国家事业后继有人的高度，全面认识做好关心下一代工作的重要性、必要性。

假设Rk代表干扰信号协方差，通信期间消耗时间的计算公式为：

式中，t0代表通信结束时间，st0代表t0时刻对应的距离，t1通信起始时间，st1代表t1时刻对应的距离，o(N)代表通信期间消耗时间。

目前，传统高速移动通信中信号模型运算节点较多，导致计算量较大，计算公式较为复杂，需要消耗大量时间来计算信号状态，这对通信效率的提升影响较大，很难满足所提出的通信实时性需求[8]。为了弥补传统信号模型的不足，本研究选取正交加权方法作为研究工具，提出新的通信节点选取方法，改善移动通信模型。

2 高速移动通信信号优化设计

2.1 移动通信模型的构建

设定高速移动通信信号矩阵为x(n)，通信延时信号矩阵为u(n)，n代表信号数量，两种信号之间的关系为：

根据此关系，计算通信信号协方差矩阵，公式为：

式中，Qn代表白噪声特征矩阵，QJ代表干扰信号特征矩阵，Qs代表通信信号特征矩阵。通过构建信号x(n)和信号u(n)之间的互协方差矩阵，分析信号周期性特点，计算信号估计值。

2.2 干扰信号处理

为了有效处理干扰信号，本研究引入正交加权算法，对干扰信号采取处理，即将导向矢量与权向量相交，使得信号中生成零陷。这种处理方法能够充分利用通信空间，对相关参数进行约束，从而得到最优解。对于本文构建的通信模型，增加正交加权算法，得到阶段性期望通信信号，此部分信号的强度较高，大大提高了抗干扰性能，符合通信模型改善需求。

2.3 提高信号接收强度方法

提高信号接收强度是高速移动通信优化目标实现的主要途径，一般情况下，以天线增益作为优化突破口，选择两个指标作为重点优化对象。对干扰信号采取抑制处理，从而降低该信号对通信质量造成的影响，另外通过提高增益数值，有效抑制信号干扰。考虑到高速移动通信期间移动速度参数数值较大，根据此关系确定入射角为：

式中，β1为移动通信初始阶段干扰信号入射环境内的角度；Δβl为作业期间信号角度的变化。如果变化量Δβl服从正态分布（方差为σ12，均值为0），则干扰信号入射角均值πsin1接近服从正态分布（方差为12，均值为πsinβ1）。其中，方差与均值之间存在的关系为：

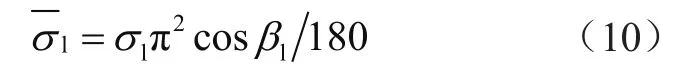
3 实验测试分析

3.1 实验测试环境与内容

为了检验本文所提出高速移动通信模型的可靠性，以通信误码率作为测试内容，运用MATLAB仿真软件环境中对不同通信方案下的通信误码率进行模拟测试。本次测试中干扰信号条件分为两种，分别是单一干扰信号、多干扰信号，针对不同环境下的通信误码率进行模拟测试。

3.2 仿真结果分析

3.2.1 单一干扰信号实验

以单一干扰信号作为实验条件，模拟不同信干比条件下的高速移动通信信号，统计不同参数条件下的通信误码率，结果如表1所示。

表1 单一干扰信号下的高速移动通信误码率测试结果

表1中，无抑制条件下，高速移动通信误码率随着信干比的增加呈现出快速下降的变化趋势，并且该条件下的误码率数值明显高于传统算法及改进算法应用下的通信误码率。当信干比为0时，3种条件下的通信误码率差异较小。相比之下，本文提出的改进算法能够有效控制高速移动通信质量，误码率比较低，并且受信干比的影响较小，稳定在8.3×10-4～9.8×10-4。虽然传统算法的抗干扰特性也很强，但是信干比不足-20时，误码率比较大，与改进算法生成的误码率拉开了比较大的差距[9]。

3.2.2 多干扰信号实验

为了进一步检验本文提出的改进算法的可靠性，检测多干扰信号条件下各个通信方案的误码率，结果如表2所示。

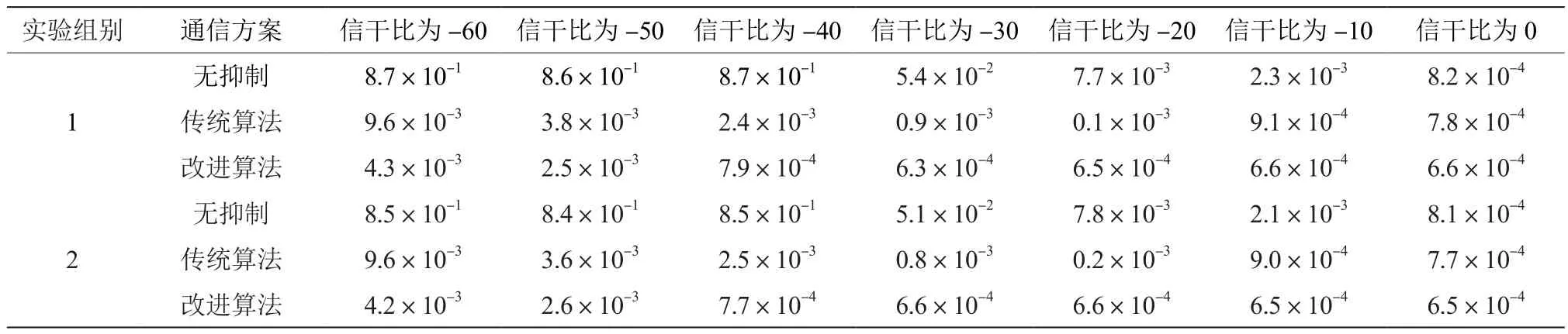
表2 多干扰信号下的高速移动通信误码率测试结果

多干扰信号对3种通信模式的信号误码率影响更大一些，信干比不足-30时，3种通信模式的误码率随着信干比的增加而下降，并且下降幅度较大。相比之下，改进算法的下降幅度最小。另外，相同信干比条件下，改进算法的通信误码率更低，当信干比超过-30时，改进算法的误码率趋于稳定，数值最小[10]。

综上仿真实验分析，本文提出的改进算法无论是在单一干扰信号条件，还是在多干扰信号条件下，高速移动通信误码率都很低，较传统算法的通信性能有所改善。

4 结 论

本文围绕高速移动通信信号干扰问题展开探究，针对传统的通信模型进行优化。该优化方案采用正交加权算法，构建移动模型，改善干扰信号对移动通信造成的影响。其中，模型优化突破口为天线增益，引入干扰信号抑制方法、通信信号增益方法，打造新的通信模型，使得信号接收质量得以改善。实验测试结果显示，本算法设计方案能够有效改善通信质量，在单一干扰信号和多干扰信号条件下，高速移动通信期间产生的误码率均有大幅度的下降。