舰艇指控系统鉴定试验数据插值方法研究*

（中国人民解放军91404部队 秦皇岛 066001）

1 引言

信息处理能力是舰艇指挥控制系统鉴定试验的关键指标之一，该项目主要的试验方法是：利用内网录取设备录取指挥控制系统生成的目标融合信息并和目标真值进行比对和分析，其中目标真值信息主要通过架设在被试舰和参试目标上的GPS或北斗设备探测得到［1］。但由于内网录取设备采样的指挥控制系统信息基本上是非连续量，同时靶场GPS设备最高提供10Hz的真值信息，使得目标真值常与指挥控制系统融合数据时戳不一致，需要进行插值处理［2］。传统的插值方法一般线性插值或三次多项式插值方法，这两种方法在对直线或低速曲线运动的目标进行真值有较好的效果［3～5］，但如果个别航次航路轨迹存在拐点、一阶导数变化率较大时或个别点出现跳变，会导致数据失真。

2 插值方法原理

2.1 多项式插值

多项式插值方法就是求解多项式函数φ(x)，使得该函数在已知点处的函数值等于给定值。最常用的是拉格朗日多项式插值法［6～8］，其插值公式为

式中i=0，1，…，n。

2.2 三次样条插值

III型边界条件：函数为周期函数情形。

其中在指挥控制系统试验中，通常III型边界条件并不适用。

2.3 三种插值方法的具体应用

以指挥控制系统对空信息处理精度试验为例，其中空中飞机目标在垂直方向上做S机动。如图1所示。

图1 飞机运动轨迹图

O为舰艇位置，曲线S为飞机真实轨迹，A（R，β，ε）为飞机被发现初始点，其中R、β、ε为飞机相对于舰艇的距离、方位、仰角，可通过机载GPS设备（10Hz）记录的飞机位置信息与舰载GPS设备记录的舰艇航迹与位置信息换算求的。由于指挥控制系统提供的飞机探测值与GPS计算求得的真值时戳不一致，需要进行真值插值处理，以距离R为例。

1）线性插值法

再结合边界条件，解出mi后，即可求得飞机瞬时位置距离的样条函数。

从上述三种方法的求解过程来看，线性插值，在飞机转弯处精度较差，三次多项式插值法不考虑数据的变化趋势，不考虑曲线连续性、平滑度。以此三次样条插值具有优势。

3 实例验证

在实验室条件下按照图2所示架设测试环境。利用剧情产生设备仿真模拟一批真值空中目标，该目标距中心点120km进入，飞行捷径P＝0±200m，飞行速度 V 为 230m/s，以 30°俯冲角，从8000m飞至2000m高度，再爬升至8000m，由远及近向站飞行距中心点17km听令转向驶出。将剧情产生设备输入雷达模拟设备生成的雷达情报信息输入指挥控制系统仿真设备，生成融合信息。

图2 测试环境架设结构图

对剧情产生设备生成的真值数据分别进行线性插值法、三次多项式插值和三次样条插值。对指挥控制系统仿真设备的融合输出利用三种插值数据进行数据处理工作，得到三种插值函数情况下的距离方位仰角一次差。

从图3～5中可得到：

图3 距离一次差

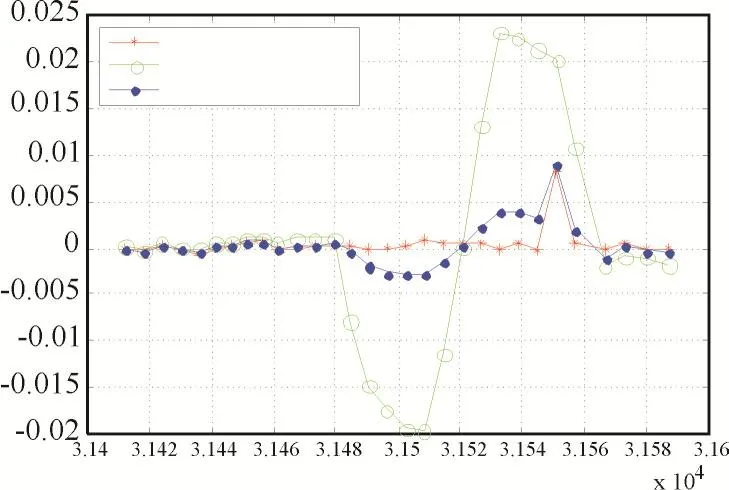
图4 方位一次差

图5 仰角一次差

1）从整体看，三次样条插值法最好，三次多项式插值法次之，分段线性插值法最差；

2）三次样条插值法对飞行目标的方位、俯仰和距离真值数据进行插值，与分段线性插值法、三次多项式插值法得出的拟合航路相比误差最小，更接近于真值航路，平滑度更好；

3）在航路拐弯处，或者航路变化较大的位置，三次样条插值法优势最为明显，分段线性插值容易出现较大失真。

4 结语

本文研究了三种常见插值法，并在实验室条件下进行了验证，结果表明，三次样条插值法克服了传统分段线性插值方法在航路拐点处或参数变化率较大情况下可能出现的拟合失真问题，且大幅度提高了拟合精度，达到了指挥控制试验对真值插值精度的要求。