中轨道Walker导航星座在轨备份方案优化设计
2021-03-16王许煜胡敏赵玉龙张学阳李玖阳
王许煜,胡敏,赵玉龙,张学阳,李玖阳
航天工程大学,北京 101400
导航星座为了满足系统对可用性、连续性和完整性的严格要求,通常会在空间部署若干颗备份卫星。若星座中有卫星失效,则通过在轨备份卫星变轨对其进行替换。如GPS(global positioning system)星座将备份卫星部署在故障概率最大的卫星附近形成“卫星对”[1],以便其中的一颗卫星发生故障时,备份卫星能够在较短时间内通过轨道机动来实现对故障卫星的快速替换[2],从而降低对用户的影响。在轨备份方案的优化设计关系到整个导航星座运行期间的服务性能,同时还涉及到空间轨道资源的维护利用等问题[3],因此必须对在轨备份方案进行合理设计。
目前,与导航星座在轨备份方案优化设计相关的研究较少。文献[3]基于系统服务性能提升,从PDOP(position dilution of precision)值、地面可见星数和地面对新增卫星可视情况3个方面对比分析了北斗卫星导航(区域)系统中GEO和IGSO备份星在不同轨位时,对现有系统服务性能的影响。文献[4]基于5GEO/5IGSO/4MEO区域导航卫星系统,在仅有2颗备份卫星的条件下利用星座的几何关系给出了同轨道面备份和异轨道面备份时,备份星IGSO的最优相位分布,从而有效地保证了系统的连续性和可用性。上述文献只对GEO和IGSO备份星轨位进行了分析,而没有考虑MEO备份星轨位的设计,同时由于GEO和IGSO轨道面内卫星数量较少,且备份星轨位相对固定,因此也都未涉及到在轨备份星替换的优化设计。
本文以中轨道Walker导航星座为研究对象,首先针对星座运行期间在轨备份星与工作卫星存在共同提供服务的情况,通过建立轨位优化模型,以PDOP值和可见卫星数为目标函数,利用NSGA-Ⅱ(non-dominated sorting genetic algorithm)算法分析在轨备份星在不同轨位下对系统服务性能的影响。其次,基于在轨备份星轨位的优化结果,建立在轨备份星替换的轨道机动模型,分别以替换所需的速度增量最少和替换时间最少为优化目标进行在轨备份星替换方案的优化设计,并分析比较两种替换方案。
1 在轨备份星轨位优化设计
1.1 轨位优化模型
在轨备份星的轨位直接决定了备份星对系统服务性能的增强效果,与星座优化设计一样,在轨备份星轨位的设计同样属于多目标优化问题。本文以中轨道Walker导航星座为分析对象,该星座由24颗卫星组成,星座参数为24/3/1,轨道高度为21 528 km,倾角为55°,同时,模型中每个轨道面上分别部署2颗在轨备份星。
(1) 优化变量
在轨备份星轨位优化设计中,模型优化变量为每个轨道面上在轨备份星的轨位fi,j,i∈(1,2,3),j∈(1,2),其中i为轨道面编号,j为在轨备份星编号。如f1,2表示第1个轨道面上的第2个在轨备份星的轨位。
(2) 目标函数
在导航星座中,定位精度是其性能评估的重要指标,而该指标除了受到各伪距测量值的影响,还与星座的几何构型有关[5],通过计算星座位置精度衰减因子(PDOP)值可以对构型进行量化评估[6]。因此,本文选取PDOP值作为备份星轨位优化的评价指标之一,其计算如下[7]。
假设用户坐标为(X0,Y0,Z0),此时在用户本地坐标系中,满足最小观测仰角α的N颗卫星坐标可表示为:
ri=[Xi,Yi,Zi],i=1,2,…,N
(1)
则相应的系数矩阵H为:
(2)
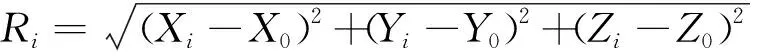
记矩阵Q为:
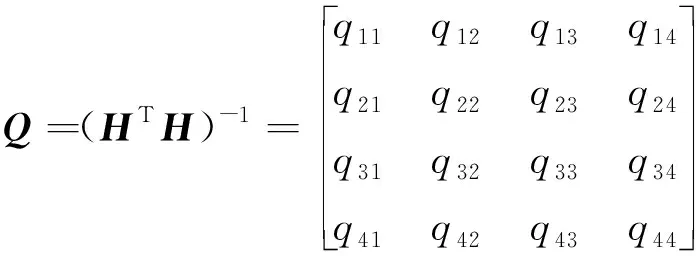
(3)
最终用户坐标的PDOP值为:
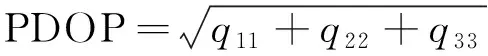
(4)
同时,导航星座除了定位精度要求外,还有其它的性能要求,本文选取可见卫星数作为另一个备份星轨位优化的评价指标。可见卫星数是指在一定的仰角范围内,用户能接收到卫星导航信号的卫星数目,其值的大小不仅决定精度因子计算结果的准确性,还与星座对地面的覆盖特性密切相关,因此同样是衡量导航星座性能优劣的重要指标。
为了更全面地评价导航星座服务区域的性能,本文采取网格分析法,对导航星座的服务区域进行网格划分,并统计在每一时刻所有网格点的PDOP值和可见卫星数,从而获得仿真时间内每个网格点的平均PDOP值和平均可见卫星数,最终对所有网格点的数值求平均,得到服务区域内PDOP值和可见卫星数的平均值,分别用FP(X)和FM(X)表示。综上可得,导航星座在轨备份星轨位优化设计的数学模型为:
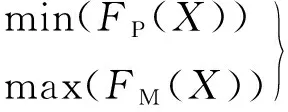
(5)
(3) 约束条件
在轨备份星轨位优化设计中,模型的约束条件为在轨备份星的轨位fi,j∈[0°,360°],同时,由于工作卫星的存在,在轨备份星的轨位不能取值为同一轨道面中已有工作卫星的轨位。
1.2 基于NSGA-Ⅱ算法的多目标优化设计
(1) 轨位优化变量的编码方式
在轨备份星轨位优化变量属于连续型变量,要利用NSGA-Ⅱ算法对其进行求解,必须对优化变量进行编码。变量编码有多种编码方式,其中应用最广泛的为二进编码方式,然而当模型优化变量取值范围较大时,为了保证优化变量具有较高的精度,需要增大二进制字符串位数,这会导致染色体基因过长,从而降低搜索效率,影响算法的收敛速度。因此,本文采用浮点数编码方法,染色体中每个基因代表一个变量,该编码方法能够有效降低染色体编码长度,提高运算效率,同时能确保变量具有较高的精度。对每个变量进行编码后,将它们串联成一个染色体,从而完成对一个个体的编码,如图1所示。

图1 染色体编码示意Fig.1 Chromosome coding diagram
(2) 基于Pareto占优的选择机制
与单目标优化问题不同的是,由于在求解过程中难以获得一个能使所有目标函数都达到最优值的理想解,当进一步优化一个目标时通常会引起其他目标的劣化,因此多目标优化问题的最优解是一组最优解集。已有大量学者对多目标优化问题的求解展开了研究并提出相应的求解思路,其中应用较为广泛的是基于Pareto 占优思想的优化方法[8]。
假设多目标优化是求解目标函数的最小值,若可行解x1所对应的任意一个目标函数值fk(x1)都小于等于可行解x2对应的目标函数值fk(x2),并且存在一个目标函数值fl(x1)小于x2对应的目标函数值fl(x2),则称可行解x1相比于x2占优或x1支配x2。
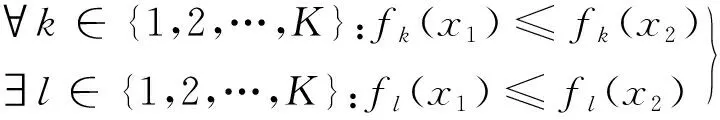
(6)
如果可行解x不被其他任一解所支配,则该可行解称为非支配解,经过算法迭代进化,可以得到所有非支配解,并组成非支配解集,称为Pareto前沿[9]。在NSGA-Ⅱ算法中采取Pareto占优的选择机制来获得Pareto前沿,其公式为[10]:

(7)
式中:μi,g为试验向量,Xi,g为目标向量。
(3) NSGA-Ⅱ算法的优化流程
非支配排序遗传算法(NSGA)是Srinivas和Deb于1994年提出的基于Pareto占优选择的多目标优化算法[11]。在此基础上,Deb等人于2002年进一步提出了NSGA的改进算法NSGA-Ⅱ[12],该算法较上一代算法的优势主要体现在NSGA-Ⅱ算法采取快速非支配排序法,从而降低了搜索非支配解的复杂度,并定义拥挤距离来计算各层中点之间的拥挤度,代替了NSGA算法中共享函数的使用,避免了人为确定共享参数对解空间分布的影响,保持了种群的多样性,同时还引入精英策略,通过对解空间进行分层确定非支配序列,保留了种群中解的优越性,也扩大了采样空间[13]。NSGA-Ⅱ算法主要包括初始化、选择、交叉和变异等步骤,其具体流程如图2所示。
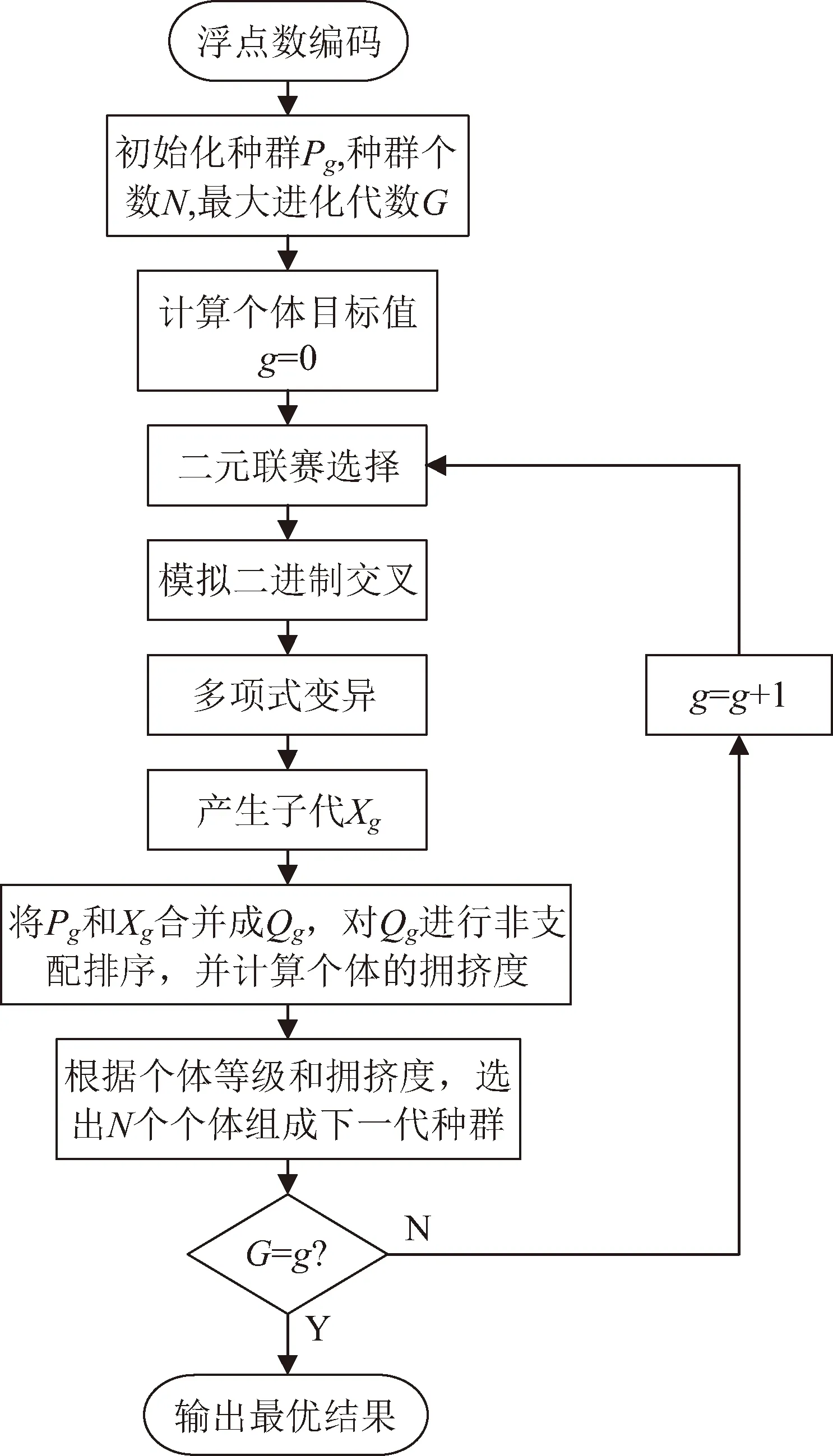
图2 NSGA-Ⅱ算法流程框图Fig.2 NSGA-Ⅱ algorithm flow chart
1.3 仿真分析
依据上述模型及优化算法对在轨备份星轨位进行优化设计,中轨道Walker导航星座的服务区域为全球区域,并按5°×5°的经纬线对其进行网格划分,仿真时间为一个星座回归周期,用户最小观测仰角α为5°,数据统计步长为600 s。优化算法的初始参数为:种群个数N为50,最大进化代数G为50,交叉因子为1,变异因子为0.16。在轨备份星轨位优化结果如图3所示。
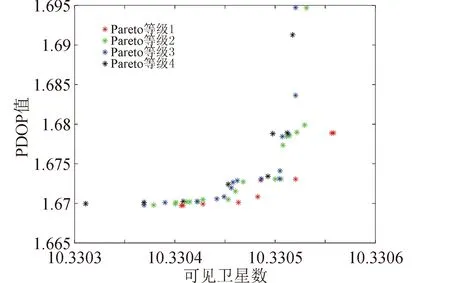
图3 在轨备份星轨位优化结果Fig.3 Optimization results of in-orbit backup satellite orbital position
从图3可得,算法迭代获得的优化解集中可见卫星数对应的区间为[10.330 3,10.330 6],PDOP值对应的区间为[1.665,1.695]。同时,对于优化解集中不同的解,其可见卫星数的变化范围较小,而且在这小范围内,不同解所对应的PDOP值呈现出随着可见卫星数增大而增大的趋势。最终,从优化解集中筛选出非支配解集,即图3中的Pareto等级1,并按照PDOP值进行升序排列,如表1所示。

表1 在轨备份星轨位的非支配解集
从表1中的非支配解集可得,可见卫星数变化范围较小,因此本文将选择非支配解集中PDOP值最小的解作为最优解,即f1,1=202.9°,f1,2=247.9°,f2,1=263.4°,f2,2=306.6°,f3,1=142.5°,f3,2=97.5°,并对其进行优化结果分析。最优解的在轨备份星轨位如图4所示,图4(b)中M11表示第1个轨道面上编号为1的卫星。


图4 在轨备份星轨位示意Fig.4 Schematic diagram of in-orbit backup satellite orbital position
针对最优解的在轨备份星轨位,对全球区域内中轨道Walker导航星座与加入在轨备份星后的星座PDOP值和可见卫星数进行对比分析,图5和图6所示的是在每个统计时刻下,全球区域内所有网格点的PDOP值和可见卫星数的平均值。可以看出,在星座回归周期内,中轨道Walker导航星座在不同时刻下PDOP平均值的最大值为1.888 9,最小值为1.875 9,平均值为1.882 4。加入在轨备份星后星座PDOP平均值的最大值降至1.6797,降低幅度为11.1%;最小值降至1.661 8,降低幅度为11.4%;平均值降至1.669 7,降低幅度为11.3%。同理,中轨道Walker导航星座在不同时刻下可见卫星数平均值的最大值为8.284 5,最小值为8.247 6,平均值为8.264 2。加入在轨备份星后可见卫星数平均值的最大值升至10.352 9,增大幅度为24.9%;最小值升至10.307 5,增大幅度为24.9%;平均值升至10.330 4,增大幅度为25%。由此可得,按照优化所得的轨位进行在轨备份星的部署,可以显著提高导航星座的服务性能。
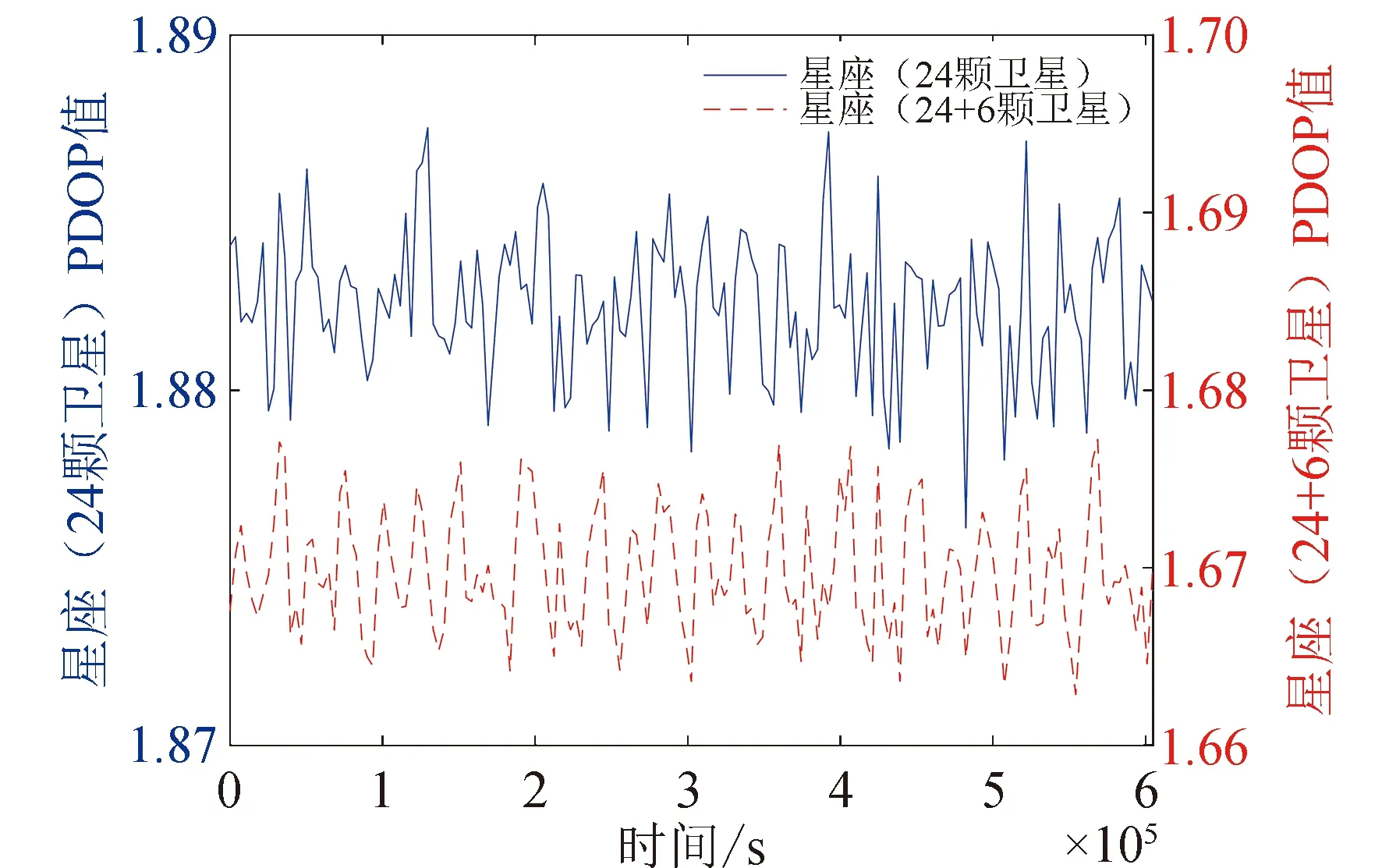
图5 星座PDOP值比较Fig.5 Comparison of PDOP values of constellation
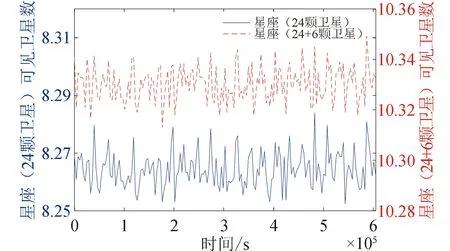
图 6 星座可见卫星数比较Fig.6 Comparison of the number of visible satellites in constellation
2 在轨备份星替换方案优化设计
在轨备份星替换方案优化设计问题不仅关系到卫星故障后导航星座服务性能的恢复,还涉及到在轨备份星替换故障卫星过程中的轨道机动问题。目前,针对轨道机动问题通常以轨道机动所需的能量和机动所持续的时间为评价指标[14]。由于卫星燃料的消耗会缩短卫星的工作寿命,而单颗卫星的寿命会极大地影响整个星座的运行周期,因此,为了最大限度延长卫星的工作寿命,保证星座的预期运行周期,应尽量减少在轨备份星燃料的消耗。同时,考虑到卫星发生故障后会导致导航星座性能的下降,从而造成相应的损失,所以,应使在轨备份星替换时间尽可能短,以确保星座服务性能尽快恢复。
本文基于在轨备份星轨位优化结果,考虑在轨备份星替换故障卫星时轨道机动所需的速度增量以及替换时间,对在轨备份星替换方案进行优化设计。
2.1 轨道机动模型
根据卫星相位调整过程中是否涉及轨道面的变化,卫星相位的调整方式可以分为同轨道面相位调整和异轨道面相位调整[15]。由于异面轨道调整所消耗的燃料较大,因此在轨备份星通常只对同一轨道面内的故障卫星进行替换。根据故障卫星相位和在轨备份星相位的关系,备份星同轨道面的替换又可以分为相位超前和相位滞后两种情况。
(1) 相位超前
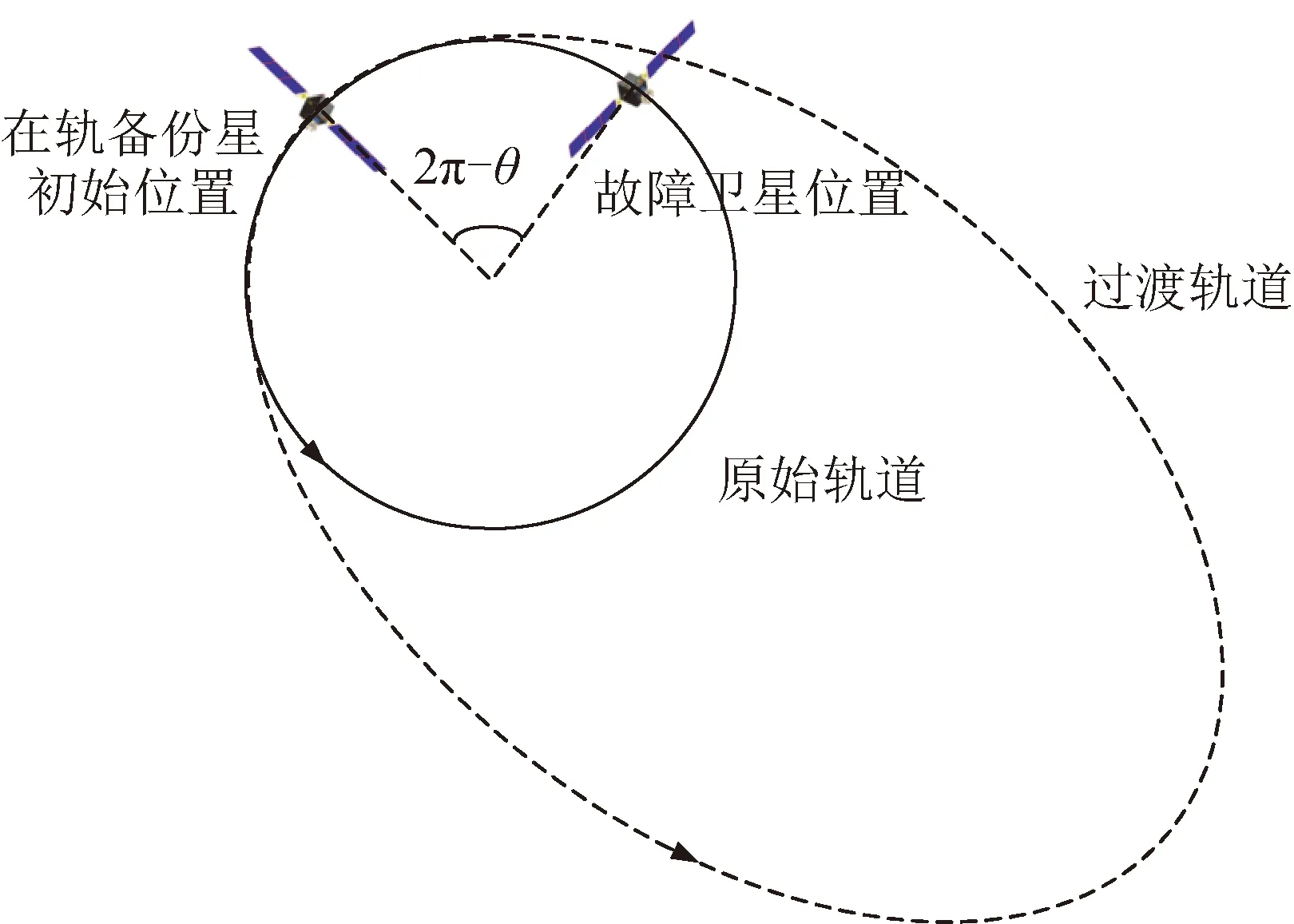
相位超前时,在轨备份星沿着运行方向到故障卫星之间的地心角θ∈[180°,360°)。此时,在轨备份星可以通过抬升轨道高度,在初始位置施加一次冲量进入高轨过渡椭圆轨道,该过渡轨道的半长轴a须满足:
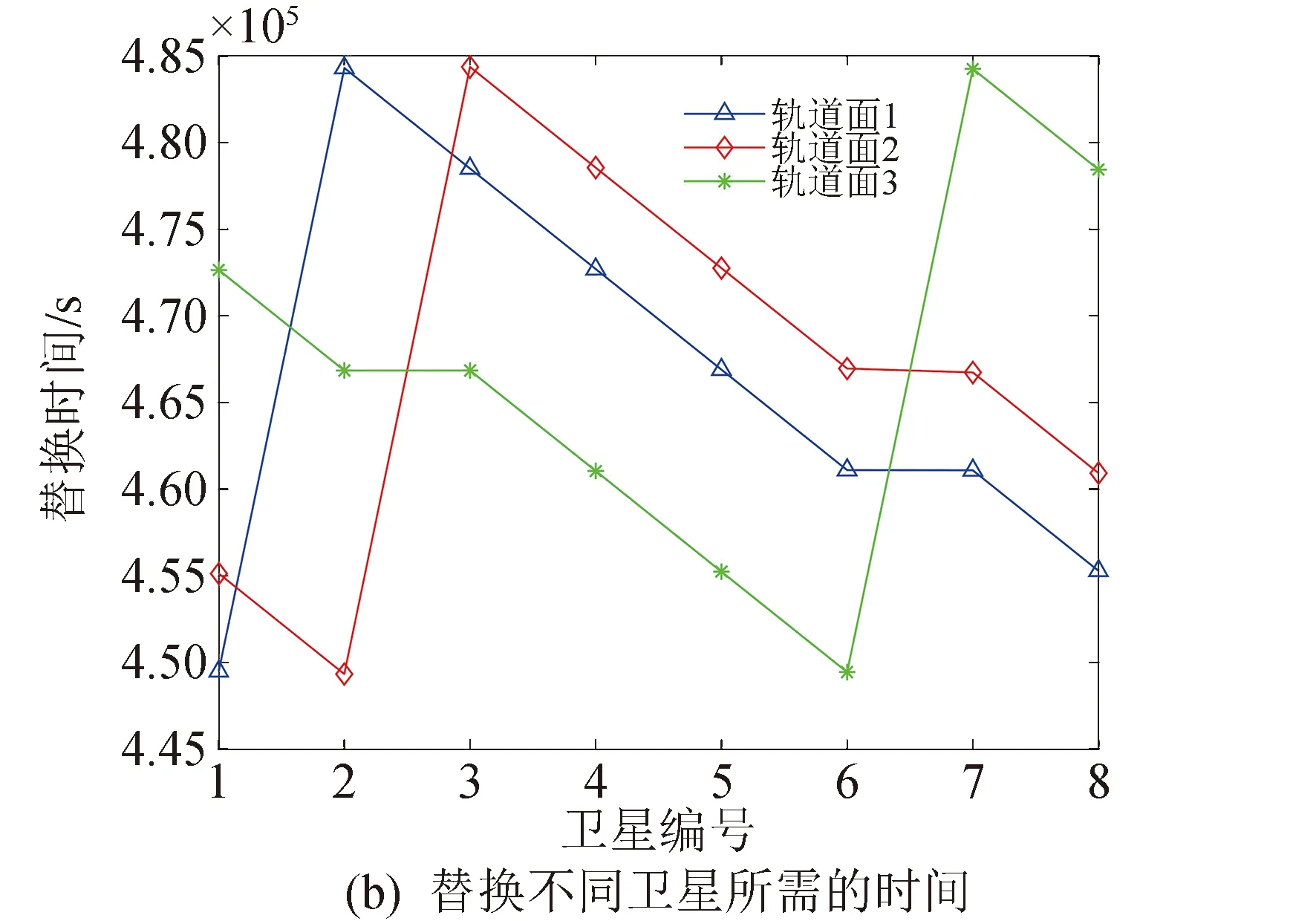
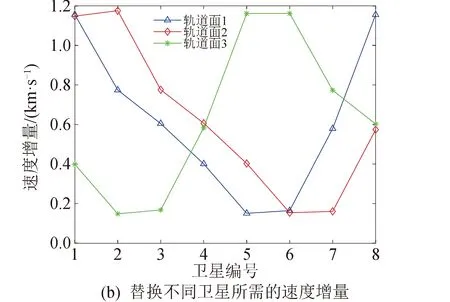
a0 (8) 式中:a0为原始轨道半长轴。 当在轨备份星在过渡轨道上运行若干圈后,故障卫星位置正好运行到在轨备份星的初始位置,此时,再对在轨备份星施加一次冲量,使其从过渡轨道进入原始轨道,即可完成对故障卫星的替换,如图7所示。 (2) 相位滞后 相位滞后时,在轨备份星沿着运行方向到故障卫星之间的地心角θ∈(0°,180°)。此时,在轨备份星可以通过降低轨道高度,在初始位置施加一次冲量进入低轨过渡椭圆轨道,该过渡轨道的半长轴a须满足: (9) 式中:R为地球半径。 图7 相位超前替换示意Fig.7 Schematic diagram of phase ahead replacement 当在轨备份星在过渡轨道上运行若干圈后,故障卫星正好运行到在轨备份星的初始位置,此时,再对在轨备份星施加一次冲量,使其从过渡轨道进入原始轨道,即可完成对故障卫星的替换,如图8所示。 图 8 相位滞后替换示意Fig.8 Schematic diagram of phase lag replacement 依据上述的轨道机动模型,可以获得在轨备份星替换故障卫星的数学模型,在轨备份星在原始轨道上的速度为v1,在过渡轨道上变轨点处的速度为v2,由于经过2次变轨,因此替换所需的总能量ΔV为2倍的速度增量。 (10) (11) ΔV=2|v2-v1| (12) 式中:μ为地球引力常数。 假设在轨备份星替换过程中,在轨备份星在过渡轨道上运行的圈数为n,故障卫星在原始轨道上运行的圈数为m,若不到1圈则为0。在轨备份星完成替换所需的时间为ΔT,则有: (13) (14) 以在轨备份星替换故障卫星时所需的速度增量最少为优化目标,分析各在轨备份星对同一轨道面上的8颗工作卫星的替换结果。由于中轨道Walker导航星座中每个轨道面分别部署了2颗在轨备份星,因此,比较2颗在轨备份星的替换结果,可以得到每个轨道面内替换不同故障卫星时所需的最少速度增量。模型目标函数为: F=min(ΔVx,y,z),x∈(1,2,3), y∈(1,2),z∈(1,2,…8) (15) 式中:ΔVx,y,z为第x个轨道面中编号为y的在轨备份星替换编号为z的故障卫星所需的速度增量。 模型约束条件为:在轨备份星相位超前时采取高轨变相,相位滞后时采取低轨变相,同时,针对实际情况,假设在轨备份星在过渡轨道上运行的圈数n和故障卫星位置在原始轨道上运行的圈数m都小于等于10。 最终以速度增量最少为优化目标的优化设计结果如图9所示,图9(a)为每个轨道面上替换不同卫星时所需的最少速度增量,图9(b)为该替换方案所对应的替换时间。从图中可以看出,速度增量的最大值为0.106 2 km/s,最小值为0.015 km/s。虽然替换所需的速度增量较小,但是替换所需的时间较长,最短的替换时间需要126.4 h,最长的替换时间则需要134.5 h。 图9 以速度增量最少为优化目标的优化设计结果Fig.9 Optimization results with the minimum increment of velocity as the optimization objective 以在轨备份星替换故障卫星时所需的替换时间最少为优化目标,再次对在轨备份星替换轨道面内的8颗工作卫星的优化结果进行分析。根据比较每个轨道面中2颗在轨备份星的替换结果,从而得到每个轨道面内替换不同故障卫星时所需的最少替换时间。模型目标函数为: F=min(ΔTx,y,z),x∈(1,2,3), y∈(1,2),z∈(1,2,…8) (16) 式中:ΔTx,y,z为第x个轨道面中编号为y的在轨备份星替换编号为z的故障卫星所需的替换时间。 模型约束条件为:在轨备份星相位超前时采取高轨变相,相位滞后时采取低轨变相,同时,在轨备份星在过渡轨道上运行的圈数n和故障卫星在原始轨道上运行的圈数m都小于等于10。 最终以替换时间最少为优化目标的优化设计结果如图10所示,图10(a)为每个轨道面上替换不同卫星时所需的最少替换时间,图10(b)为该替换方案所对应的替换速度增量。从图中可以看出,以替换时间最少为优化目标时,替换卫星所需的最短时间为8.8 h,最长替换时间为18.5 h,极大地缩短了替换所需的时间。同时,替换所需的速度增量虽然比以速度增量最小为优化目标时的大,但速度增量最大值为1.16 km/s,最小值为0.14 km/s,仍处于较低水平。 图10 以替换时间最少为优化目标的优化设计结果Fig.10 Optimization results with the minimum replacement time as the optimization objective 基于上述对两种替换方案的分析可得,以速度增量最少为优化目标的轨道机动方案,虽然所需的能量较少,但是替换所需的时间较长,适用于主要考虑节省能量的星座;而对于需要快速恢复服务性能的导航星座而言,该替换方案并不十分合适。而以替换时间最少为优化目标的轨道机动方案,其最长的替换时间和最短的替换时间分别降低了86.25%和93.04%,因此该方案能够在很大程度上减少替换时间;同时,速度增量较以速度增量最小为优化目标的替换方案有所增加,备份星单次机动的速度增量最大值为0.58 km/s,最小值为0.07 km/s,而对于卫星轨道机动而言,该值仍保持在较低水平。综合两种替换方案,本文选用以替换时间最少为优化目标的替换方案作为在轨备份星替换的最终方案。 本文对中轨道Walker导航星座在轨备份方案进行了优化设计,得到以下结论: 1)NSGA-Ⅱ多目标优化算法能够有效实现在轨备份星轨位最优解的快速求解,最终在轨备份星轨位的最优解为:f1,1=202.9°,f1,2=247.9°,f2,1=263.4°,f2,2=306.6°,f3,1=142.5°,f3,2=97.5°。 2)按照本文所得的轨位设计方案进行在轨备份星的部署,可以显著提高导航星座的服务性能,在回归周期内,导航星座在全球服务区域上的PDOP值和可见卫星数的平均值分别降低了11.3%和提高了25%。 3)通过分析比较以速度增量最少和以替换时间最少为优化目标的替换方案,可得以替换时间最少为优化目标的替换方案能够在短时间内以较低的能量完成卫星的替换,更符合导航星座的需求。



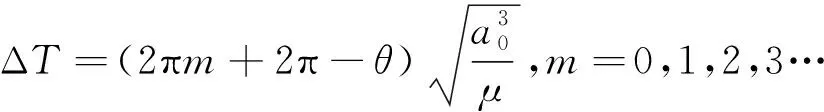
2.2 以速度增量最少为优化目标

2.3 以替换时间最少为优化目标

2.4 结果分析
3 结束语
