Klobuchar电离层模型误差分析及预测

2021-03-16彭雅奇李冲辉王倚文魏武雷丁柏超刘仰前

中国空间科学技术 2021年1期

彭雅奇，李冲辉，王倚文，魏武雷，丁柏超，刘仰前

1. 中国直升机设计研究所天津直升机研发中心，天津 300000 2. 北京理工大学宇航学院，北京 100081

电离层作为空间环境的重要组成部分，能够对无线电信号产生反射、折射以及散射等效应，使导航信号的传播速度和方向发生改变，从而造成电离层延迟误差，该误差是GNSS测量中的重要误差源之一[1-3]。改正电离层延迟可以采用双频或多频组合来进行消除，而在单频接收机用户中，Klobuchar电离层模型以其复杂程度小、方便利用的优点得到广泛应用[4-6]。该模型利用8个基本参数直观简洁地反映了电离层的变化特性，也充分考虑了其周期和振幅的变化，可在实际应用中进行快速电离层误差改正[7-8]。

然而，8参数Klobuchar电离层模型的改正精度不高，通常仅能达到60%左右，不能满足日益增长的精度需求[9-10]。许多研究学者从不同方面对该模型提出过改进，刘宸等[11]提出在原模型8参数的基础上增加5个关键参数，采用松弛迭代与直线搜索中的黄金分割相结合的算法，构建区域改进模型，将改正精度提升至77.51%；章红平[12]提出14参数的Klobuchar模型，用增加的6个参数描述初始相位及夜间平场的变化，使得中国区域的电离层改正精度得到提高。蔡成辉等[13]通过采用最小二乘拟合对初始相位和振幅进行改正，建立了适用于小区域的Klobuchar电离层延迟改正模型。文献[14]在不增加参数的前提下，为了更准确描述极地地区的电离层变化，基于夜间项和余弦项的振幅进行改进，针对单频GNSS用户建立了修正Klobuchar模型。国内外大部分研究成果虽然从各方面对模型进行改进并取得较好的改正效果，但仍存在对电离层整体改正率不高，不足以反映夜间电离层变化等不足。

本文通过对比iGMAS的高精度电离层格网数据，对Klobuchar电离层误差进行了基于全局和基于时间序列的误差分析。结果发现，尽管Klobuchar模型相对比较粗糙，但是在中纬度区域，模型误差却呈现出一定的周期性特征。基于此本文利用粒子群优化(particle swarm optimization, PSO)结合反向传播神经网络(back propagation neural network, BPNN)，建立PSO-BPNN的电离层误差预测模型，通过对误差数据的训练学习，掌握输入输出间的非线性映射关系，对中纬度Klobuchar电离层模型误差进行预测和补偿，从而提高该区域Klobuchar电离层模型的精度。

1 Klobuchar电离层模型误差分析

1.1 Klobuchar电离层模型

在GPS所采用的Klobuchar模型中，用余弦函数拟合白天的时延变化，将每天电离层的最大延迟固定在下午两点(本地时间)，夜间电离层天顶时延被视作一个5 ns的常量，转换成电离层总电子含量(total electron content，TEC)则为9.23 TECU(1 TECU=1016个电子每平方米)，Klobuchar模型利用8个模型参数和电离层穿刺点处的地磁纬度进行计算，并通过映射函数转换为传播路径上的电离层延迟，具体模型可参考文献[15]，此处不再赘述。

1.2 iGMAS电离层产品

iGMAS能够对GNSS系统服务性能(定位精度、连续性、可靠性等)进行监测评估，并生成高精度精密星历、卫星钟差和全球电离层TEC格网等产品，在这些核心产品中，全球电离层TEC格网已经成为研究电离层延迟改正的重要基础数据。

iGMAS导航数据分析中心综合GPS全球网选出250个适于解算电离层的测站，将每天的TEC变化按每2 h的时间间隔，全天共反演生成12张全球电离层TEC地图产品，其沿纬度和经度方向的数据点间隔分别为2.5°和5°，最后以IONEX(ionospheric map exchange，IONEX)格式对外发布[16]。根据iGMAS官方数据显示最终电离层TEC格网数据精度在2～8 TECU，精度在90%以上，因此本文将其视为电离层TEC真值，在此基础上进行误差分析。

对于任意时刻穿刺点的TEC的求解，可以采用双线性内插的方法，在对时间、经度和纬度进行内插后，就可获得某时某地的TEC数据，对应的垂直方向电离层路径延迟为：

(1)

式中：f为对应的系统工作频率。

1.3 误差分析

本文的Klobuchar模型参数从武汉大学IGS数据中心下载的广播星历头文件中提取。为了简化问题和方便数据提取，本文主要对穿刺点垂直方向上的电离层误差进行分析，传播路径上的电离层延迟可通过映射函数进行转换。

对比分析2019年10月1日10时的Klobuchar电离层误差，首先根据iGMAS给出的高精度电离层格网数据绘制出该时刻的全球电离层图(global ionosphere maps, GIM)，由于GIM图的单位为TECU ，为了进行误差分析，需将单位进行统一，根据式(1)可将其转换为穿刺点垂直方向路径延迟(单位为cm)，本文将其视为真实电离层延迟，如图1所示。

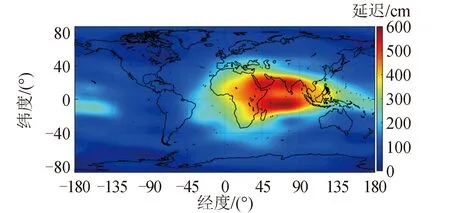
图1 真实电离层延迟Fig.1 True ionospheric delay

图2 基于全局的Klobuchar电离层延迟误差分析Fig.2 Error analysis of global Klobuchar ionospheric delay

以L1信号为例，fL1=1 575.42 MHz，如图2所示,计算同一时刻的Klobuchar电离层路径延迟误差。可以看出，Klobuchar模型相对比较粗糙，与真实延迟相比仅能大致拟合电离层的分布，在电离层延迟峰值附近仍然存在不小的误差。

图3 基于时间序列的Klobuchar电离层延迟误差分析Fig.3 Error analysis of Klobuchar ionospheric delay based on time series

在基于时间序列的纵向误差分析中，分别选取电离层相对活跃年份(2016年)和相对平稳年份(2019年)进行一周内的误差分析，由于高纬度极地地区电离层延迟相对较小，而其变化又很无常，导致Klobuchar电离层在此区域的适用度较低，因此本文着重分析低纬度和中纬度的误差变化特性，结果如图3所示。可以看出，活跃年份的电离层延迟比平稳年份的要大，但共同点是Klobuchar模型计算的电离层延迟与真实延迟都存在不小的误差，同时也能够发现在中纬度电离层误差的变化比较规律，存在以天为频率的周期性变化特征，尤其在平稳年份更加明显。

2 PSO-BPNN电离层误差预测模型

2.1 标准BPNN模型

BPNN属于人工神经网络的一种，以其良好的非线性表达和学习能力，受到较多工程领域人员的青睐，它是一种包含多层网络(输入层、隐层、输出层)的逆推学习算法[17]，其结构如图4所示。

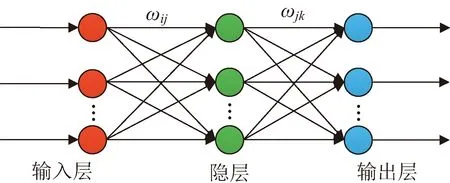
图4 BPNN模型结构Fig.4 BPNN model structure diagram

ωij和ωjk为网络权值，利用实际输出与期望输出的差值来调整网络连接权值，通过大样本的数据进行训练学习，使得网络权值不断优化，误差也不断减小。

2.2 PSO-BPNN误差预测模型

标准BPNN模型对于网络初始参数(如权值、阈值、学习速率等)的设置较为敏感，同时也比较容易陷入局部极小值。PSO算法能够较好地克服BPNN模型的缺点，可以基于种群信息在全局范围内寻找最优解，在BPNN模型优化方面已经得到了非常成熟的应用[18-19]，因此本文也将基于PSO-BPNN构建Klobuchar电离层误差预测模型，具体过程如下：

1)获取样本数据集并进行数据预处理。通过Klobuchar电离层模型计算所得延迟数据与iGMAS高精度电离层产品进行对照，得到Klobuchar模型误差。需要注意不同参数的量纲往往不同，因此为了消除参数量纲对结果的影响，需要进行归一化预处理，将各参数统一至同一数量级。

2)确定神经网络结构及输入输出。模型输入参数为电离层穿刺点处的位置参数(经度、纬度)以及时间参数(周内秒、小时数)，输出层对应Klobuchar电离层模型误差，故输入层节点数m为4，输出层节点数n为1，隐层节点数l可通过经验公式来确定：

(2)

式中：a为1～10之间的整数，可根据实际进行调整。

3)初始化粒子群及粒子个体的位置和速度。每个粒子的位置表示为Xi=(xi1,xi2,…,xid)T，速度表示为Vi=(vi1,vi2,…,vid)T，其中d=ml+ln+l+n，为粒子群个体搜索的空间维数。

4)计算粒子适应度函数。表达式为：

(3)

式中：M表示训练样本个数；Ti为系统的期望输出值；Pi为系统的预测输出值。根据适应度函数评价粒子的优劣程度，以此来更新个体最优值和全局最优值，将个体粒子搜索到的最优位置记为Pbest，整个粒子群搜索到的最优位置记为Gbest。

5)更新粒子位置速度。通过不断更新迭代个体最优值和全局最优值来引导粒子群进行空间搜索，进行粒子位置和速度更新：

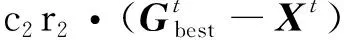
(4)

Xt+1=Xt+Vt+1

(5)

式中：w为惯性权重；t为算法当前的迭代次数；c1和c2为学习因子；r1和r2为[0,1]之间的随机数。

6)迭代计算输出最优粒子。PSO算法的迭代终止条件为达到预设精度或最大迭代次数，满足终止条件时便可将最优粒子映射到BPNN的权值和阈值。

7)神经网络模型训练。根据样本数据集训练BPNN，得到PSO-BPNN电离层误差预测模型。

整个模型流程如图5所示。

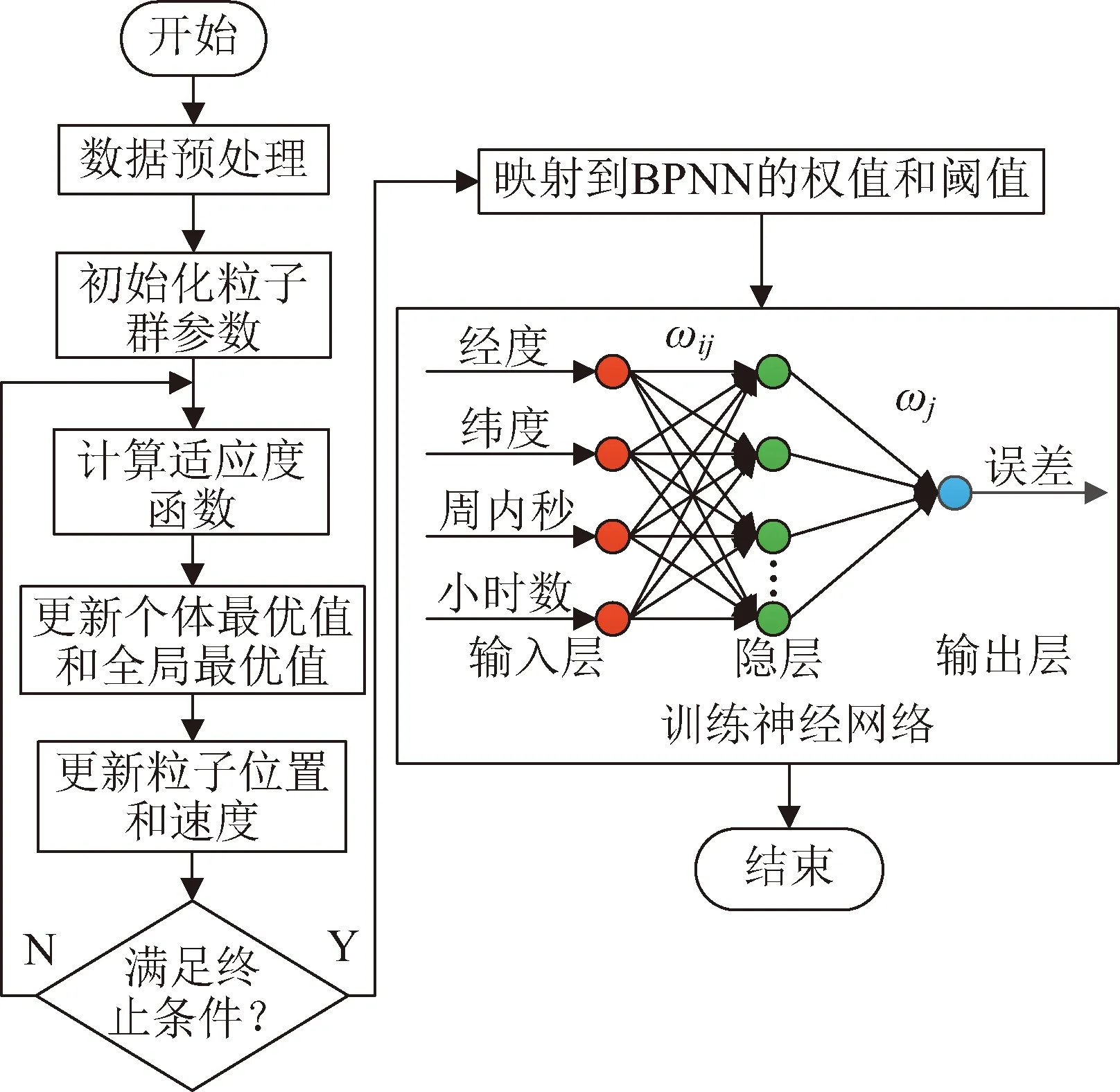
图5 PSO-BPNN模型流程Fig.5 PSO-BPNN model flow chart

3 Klobuchar电离层模型误差预测

应用PSO-BPNN模型可以对Klobuchar电离层误差进行预测，本文选用2019年10月1日起25天的数据对神经网络进行训练，然后预测之后10天的电离层误差。为增强BP算法的数据表征能力，隐层激励函数选择双曲正切函数tansig，而输出层应具有较大的变化范围，故激励函数选择线性传输函数purelin，设定学习速率为0.01，最大训练次数为500次；PSO种群规模为100，迭代次数为50，惯性权重为0.9，学习因子c1=c2=2，预设误差为0.01。本文在全球范围内选取4个中纬度穿刺点为例进行误差预测，坐标分别为P1(30°(N),100°(W))，P2(45°(N),110°(E))，P3(40°(S),70°(W))，P4(25°(S),135°(E))，如图6中标记所示。

利用MATLAB对模型进行仿真，结果如图7所示，从图中可以看出，利用PSO-BPNN电离层误差预测模型可以预测Klobuchar模型误差的大致趋势，将两者作差后得到的预测偏差处于一个相对较低的水平，证明了该模型对于中纬度电离层误差预测是有效的。

但是随着时间的推移，每天Klobuchar模型误差变化的峰值会存在波动，波动大的时候，误差预测模型并不能很好的进行跟随，其预测精度就会下降，不过整体上仍然可以减小Klobuchar模型的误差。

图6 试验点选取分布Fig.6 Distribution map of test points selection

图7 试验点的模型预测偏差Fig.7 Prediction bias of test points

将PSO-BPNN电离层误差预测模型的预测值补偿进Klobuchar模型中，即可提高模型的改正精度。通过计算本文模型的预测偏差均值，与Klobuchar模型误差均值作比较，如表1所示。可以看出，在中纬度地区，利用Klobuchar模型计算电离层延迟仅能将误差改正为原来的60%左右，仍然存在较大误差，而利用PSO-BPNN模型补偿后可将电离层延迟误差改正为原来的90%左右，平均精度可提高30%左右。