挠性航天器多目标鲁棒姿态控制的DPSO算法实现

王梦菲，张军,*

1. 北京控制工程研究所, 北京 100190 2. 空间智能控制技术国家级重点实验室，北京 100190

由于未建模动态和建模的不确定性，标称模型下设计的控制器在实际中性能会出现偏差。在轨时航天器常受到内外干扰作用，特别是带有大型挠性子结构的现代航天器，其挠性结构易受干扰激发产生振动，严重影响姿态指向精度和稳定度，甚至导致航天器失稳，如美国的Explore I[1]。因此，大型挠性航天器高精度、高稳定度姿态控制是一个热点问题也是控制界的难题。

文献[2-4]研究了经典PID控制方法在挠性航天器姿态控制中的应用；当模型存在不确定性、未建模模态发生振动以及耦合振动发生变化时，其控制性能下降，且PID控制对外部干扰的鲁棒性也有待加强。文献[5]针对结构振动，基于状态反馈设计了时间最优的LQR控制器，但不适合高频范围内未建模模态的振动抑制，且不能满足模型不确定性时的鲁棒控制。文献[6]改进了自适应滑模控制方法，最大限度地减少了不确定性、扰动和柔性动态坐标测量等带来的困难，并在一定程度上改善了滑模控制固有的抖振现象。文献[7]证明了基于姿态角和角速度的反馈对于大范围摄动的稳定性，并针对含参数不确定性和未建模动态的姿态控制系统，设计了基于线性矩阵不等式(linear matrix inequality, LMI)的鲁棒H∞控制器。文献[8]针对挠性航天器姿态机动问题，以姿态达到目标角度且保持稳定的时间为适应度值，将粒子群优化(particle swarm optimization, PSO)算法与黄金分割控制等结合，设计了一种离线控制器；相对于常规的控制方法，该方法的优点在于：可根据系统实际动力学特性和控制要求选择最优机动路径，实现姿态快速机动和稳定。文献[9-11]将神经网络、模糊控制理论应用于姿态控制系统设计；但模糊控制效果往往依赖于操作者经验；为提高可靠性，神经网络一般需在线学习，受星载计算机限制。

上述挠性航天器姿态控制方法大多是针对单一控制目标而设计的，但在工程实际中，控制系统的设计需考虑鲁棒性、快速性、精度和执行机构输出饱和等多目标要求，这就属于典型的多目标设计问题，关于此类问题的研究较少。

针对上述多目标鲁棒控制问题，本文在自适应PSO算法中加入变异操作，提出一种差分粒子群优化(differential particle swarm optimization, DPSO)算法，以提高粒子的多样性和搜索性能；同时将该算法与鲁棒D-稳定极点约束以及Pareto最优结合，涉及的数学公式较少，设计灵活。相比于传统带极点配置的LMI方法，本文方法不受特定指标和约束模式的限制，可避免凸优化过程，并减小求解的保守性[12]。相对于文献[13-14]提到的借助特征结构配置的参数化方法，本文优化过程无需将多目标转化为一个加权目标函数，可避免加权系数的选择困难，特别是多目标存在矛盾关系的情况；而且文献中方法需将指标转化为特定的参数化形式，对参数摄动敏感度的优化无法保证系统鲁棒稳定。本文方法适用的指标形式更广，能实现所允许的参数不确定范围内的鲁棒D-稳定；可为大型挠性航天器鲁棒控制器设计提供一种思路。

1 挠性航天器动力学模型

带有一对太阳翼的航天器姿态动力学方程可表示为[15]：

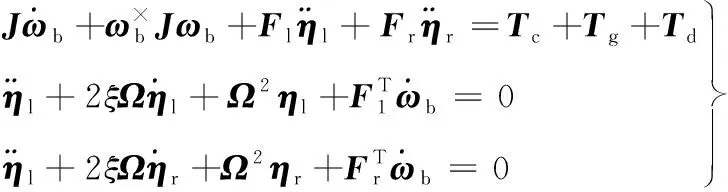
(1)

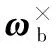
本文仅考虑航天器姿态定向保持和姿态镇定情况，假设姿态为小角度，此时姿态运动学为

(2)

Tg=Agθ

(3)

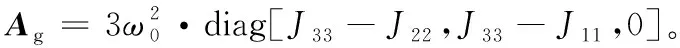
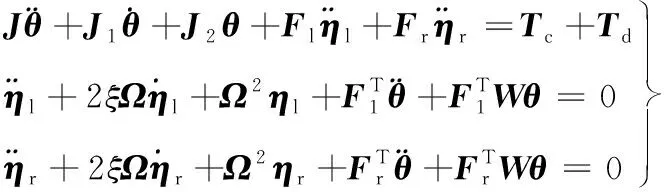
(4)

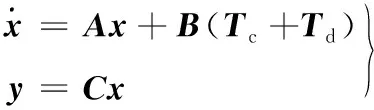
(5)

考虑模型不确定性，矩阵A、B可表示为[16]：

式中：下标0表示为标称系统下的矩阵；D、F1和F2为适当维数的常矩阵；Δ为未知矩阵且满足ΔTΔ≤I。忽略二阶不确定项并只考虑转动惯量的不确定性可得：

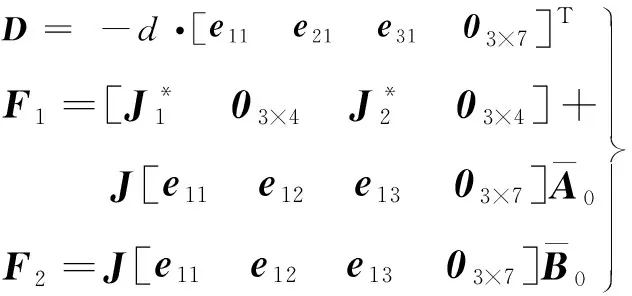
(6)

式中：d∈[0,1)，当d=0时系统不存在不确定性；

diag[4(J22+J33),3(J11+J33),J11+J22]

当不考虑挠性模态时，e12、e13、e21、e31均为零矩阵。

证明：首先推导矩阵相加求逆结果，如对于矩阵M有(M+ΔM)-1=Μ-1+N，其中ΔM为不确定项，N为待求解的矩阵。将等式两边分别左乘M+ΔM得：

于是

(M+ΔM)-1=Μ-1-(MΔM-1Μ+Μ)-1

同理可推导：

保留ΔM的一次项，近似可得

(M+ΔM)-1=Μ-1-M-1ΔMM-1

那么忽略二阶不确定项，考虑转动惯量的不确定性有：

记

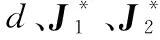
(7)

同理可得：

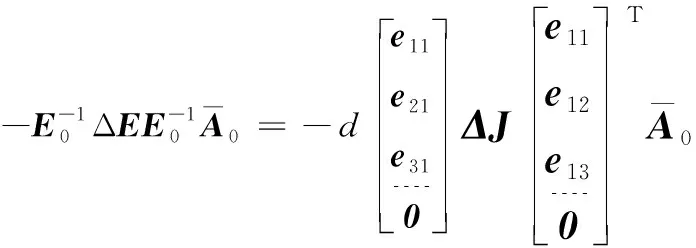
(8)

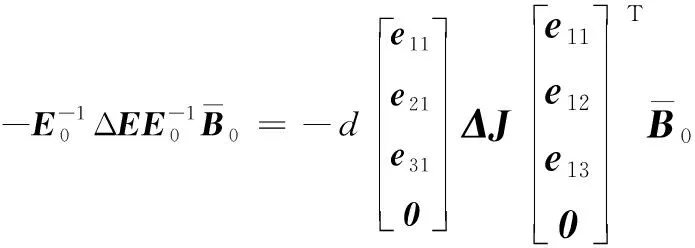
(9)

由式(7)～(9)可得式(6)。得证。

2 鲁棒控制器智能优化设计

2.1 智能优化算法介绍

(1)PSO算法

PSO算法是一种受鸟群觅食启发的随机搜索算法[17]，具有结构简单、参数少和搜索速度快等优点，已广泛应用到自然科学和工程科学多个领域。该算法中速度和位置更新如下。

式中：k(k=1,2,…,G)为当前迭代次数，G为最大迭代次数；vi和xi分别为第i个粒子的速度和位置向量，取值区间分别为[vmin,vmax]和[xmin,xmax]，i∈{1,…,N}，N为群体个体总数；pi和g分别为个体及全局极值，pbest(i)、gbest为对应的适应度值；c1、c2为加速常数即学习率；r1、r2为[0，1]范围随机数；w(k)=wmax-k(wmax-wmin)/G为惯性权重，取值区间为[wmin,wmax]。

(2)差分进化(differential evolution, DE)算法

DE算法是一种鲁棒性较强的随机搜索算法，其基本思想来源于遗传算法，这里选取差分进化算法DE/rand/1/bin策略，种群参数定义同上述PSO算法，关键步骤如下[18-19]。

1)变异,计算变异向量:

υi(k+1)=xl1(k)+F(k)·[xl2(k)-xl3(k)]

2)交叉，计算试验变量：

式中：交叉算子CR=0.3×[1+rand(0,1)]；randb(j)表示产生[0,1]之间随机数发生器的第j个估计值；rnbr(i)∈(1,2,…,D)表示一个随机选择的序列，以确保ui至少从υi中获得一个参数。

3)选择，DE算法按照贪婪准则将试验向量ui(k+1)与当前种群中的目标向量xi(k)进行比较，较优的向量将在下一代种群中出现。

(3)DPSO算法

DPSO算法在PSO算法的基础上加入DE算法的变异操作，在保证粒子群朝着好的方向发展的同时增加了粒子的多样性，提高粒子的全局搜索能力，有效避免了早熟至局部最优解的情况[20]。算法流程和部分参数定义同PSO算法，其速度和位置更新如下。

(10)

F(k)定义同DE算法，r3为[0，1]范围内的随机数，xU(k)和xL(k)为当代粒子中的较优和较劣解，以保证粒子向有益的方向发展。

2.2 多目标约束描述

由于挠性模态难以观测或直接测量，本节参考文献[7]，采用姿态角和角速度反馈设计控制器，下面关于多目标约束的描述建立在此基础上。

考虑转动惯量的不确定性和未建模动态、各种干扰对系统的影响，以及避免控制饱和的现象，本节在控制器设计时加入鲁棒D-稳定约束，并对控制能量和内外干扰抑制相关指标进行优化。极点约束和两个典型优化指标的显示表达以及Pareto最优理论描述如下。

2.2.1 鲁棒D-稳定

(1)含挠性模态

设稳定裕度参数为h(h<0)，那么式(5)系统对应如图1所示，鲁棒D-稳定实现为：

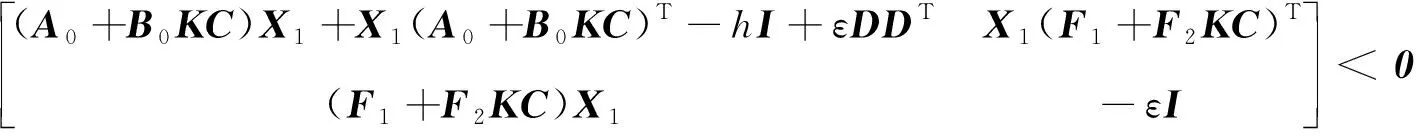
(11)

式中：K∈Rm×n为相应维数的反馈增益矩阵，在优化的过程中视为已知，此时控制输入u=BKy；ε>0为标量。优化时可将标称系统下的挠性模态极点限制在一定变化范围内，如实部区间为[a1,a2](a1,a2<0)，虚部绝对值区间为[b1,b2](b1,b2>0)。

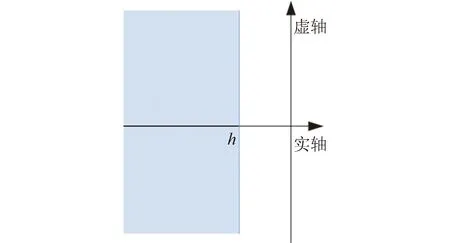
图1 极点配置区域(1)Fig.1 Pole assignment region(1)

证明：参考文献[16]，考虑不确定性和保证系统一定的鲁棒稳定裕度有：

P[(A0+ΔA)+(B0+ΔB)KC]+

[(A0+ΔA)+(B0+ΔB)KC]TP-hI<0

式中：P为对称正定矩阵。记Y=P(A0+B0KC)+(A0+B0KC)TP-hI，则有

Y+PDΔ(F1+F2K)+

(F1+F2K)TΔT(PD)T<0

上述矩阵不等式对所有满足ΔTΔ≤I的不确定矩阵Δ成立，当且仅当存在ε，使得

Y+εPDDTP+ε-1(F1+F2K)T(F1+F2K)<0

应用矩阵的Shur补性质，可以等价为：

上式左右同乘矩阵diag{P-1,I}，并记X1=P-1，便可得到式(11)，得证。

(2)不含挠性模态

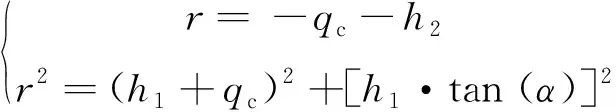
针对不确定系统，对给定区域D，若存在对称矩阵X1、X2和标量ε1、ε2>0同时满足：

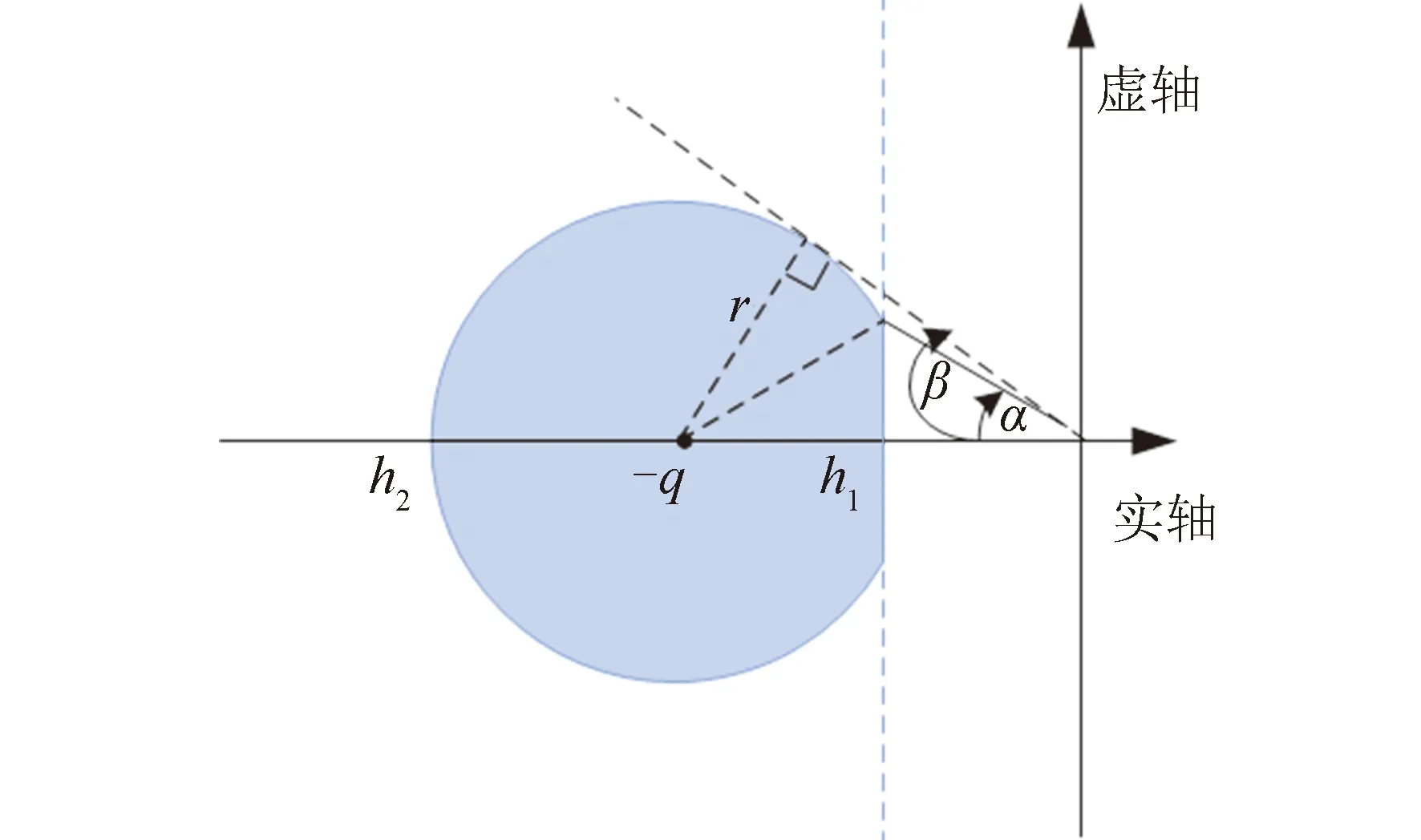
图2 极点配置区域(2)Fig.2 Pole assignment region(2)

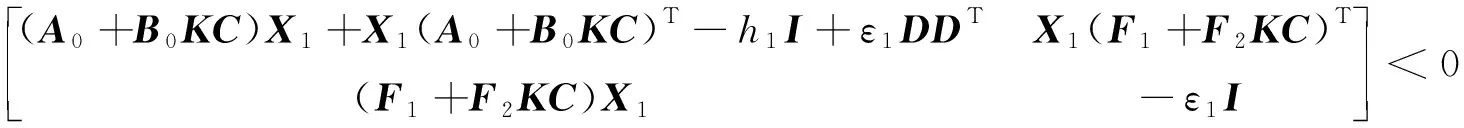
(12)

(13)

式中：A0、B0、C不含挠性模态信息且此时C为是单位阵；此处X1可不等于X2，ε1可不等于ε2，以减小保守性。则该不确定系统为鲁棒D-稳定。证明过程同式(11)。

2.2.2 (内外)干扰抑制能力

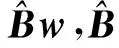
式中：Ac=A+BKC。建立从w到y的传递函数矩阵Gyw(s)，那么根据H2控制理论思想，用‖Gyw(s)‖2定义干扰对输出影响的大小[13]：

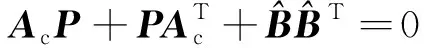
2.2.3 控制能量

现代航天器多以动量轮或控制力矩陀螺为姿态控制执行机构，为防止因执行机构饱和而导致的系统性能变差或失稳现象，需加入控制能量约束。直接将饱和非线性因素加入控制器设计会带来分析困难，所以参考文献[13]，基于航天器姿态定向保持时姿态角偏差和姿态角速度均为小量的特点，通过优化‖K‖2的值来尽可能减少控制能量‖u‖。记

f2(K)=‖K‖2

2.2.4 Pareto最优原则

一般优化指标之间的关系难以确定，且不乏相互冲突的情况，因此无法找到多目标均为最优的唯一解，只能找到在多目标间平衡的次优解，此时需应用Pareto最优解的概念。假设存在性能指标函数f1(x),…，fs(x)(s≥2)，其中x为搜索空间φ中的向量，与K对应，有如下定义：

x=[K(1,1),…,K(1,n),K(2,1),…,

K(2,n),…,K(m,n)]

Pareto最优解：如果不存在同时满足下式的x∈φ，那么x*∈φ则为Pareto最优解或非劣解(此解不唯一)[21]：

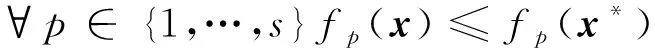
(14)

(15)

如果存在满足上述条件的解x，那么则称该解Pareto占优于解x*。

创建由粒子每代更新产生的非劣解和占优解组合而成的外部解集；因为想得到每个指标都相对较优而不是某单个指标最优的解，所以为了提高算法的快速性，不按拥挤度法[12]而是按距离评价法更新该解集，保留距离较小的解。做归一化处理，对应x的距离d(x)定义如下：

式中：maxfs和minfs分别表示第s个目标函数在外部解集中取得的最大和最小值。以s=2为例，如图3所示。

图3 距离评价法Fig.3 Distance evaluation

2.3 多目标鲁棒控制器设计流程

基于DPSO算法的控制器设计步骤如下。

步骤1：初始化粒子群。包括算法参数和位置、速度向量，其中初始位置向量由PID控制下的增益矩阵和LMI方法下求得的几组反馈增益矩阵定义，初始速度向量为零向量；初始化粒子i(i=1,2,…，N)的历史最优位置pi和最优值p1best(i)和p2best(i)并选取第一个粒子为全局最优粒子，对应位置g和最优值g1best和g2best。迭代次数k=1，且xU(k)=xL(k)=x1(k)。

步骤2：更新粒子速度和位置。k=k+1；按式(10)更新速度和位置，并做边界条件处理；判断是否满足鲁棒-D稳定极点约束，若满足进入步骤3，否则进入步骤6。

步骤3：更新个体粒子最优解和全局最优解。计算个体粒子适应度值(性能指标)f1(xi),f2(xi)，按Pareto占优更新最优解；将每个粒子当代更新的非劣解和占优解存入外部解集。

步骤4：更新外部解集。计算解集中每个解对应的距离，找到距离最短的解，然后将其他解对应的适应度值与该解比较，保留下非劣解和占优解；判断保留下的解的个数是否大于集合上限N，若是，进入步骤5，否则剔除距离较大的部分解。

步骤5：计算xU(k)和xL(k)。计算各粒子的适应度值f1(xi),f2(xi)，并求取所有粒子适应度值的平均值；将每个粒子对应的适应度值与平均值比较，在Pareto占优的粒子中任选一个将其解作为xU(k)，在剩余粒子中任选一个将其解作为xL(k)；当不存在Pareto占优的粒子时，xU(k)=xL(k)，取任意粒子位置向量。

步骤6：判断是否满足k≤G，如满足返回步骤2，否则进入步骤7。

步骤7：画图，并定义仿真参数。

3 仿真校验

以某大型航天器为例，取其一对翼板的前两阶挠性模态进行控制器设计和仿真。标称系统转动惯量、耦合系数、帆板挠性约束模态角频率对角阵和阻尼系数分别为：

图2中参数α=50°，h1=-0.2，h2=-0.02；挠性模态极点相关参数h=-0.001，a1=-0.03，a2=-0.001 5，b1=0.25，b2=0.35。优化算法参数取值如表1所示；以控制能量为适应度值为例，PSO、DE和DPSO三种算法的对比优化结果见图4。

从图4可看出DE算法进化较慢，PSO算法过早收敛，容易陷入局部极值，本文提出的DPSO算法寻优能力最好，因此采用DPSO算法进行多目标优化。图5为基于Pareto最优原则的多目标优化结果，可以看出在距离评价法下，外部解集中的非劣解集合接近Pareto前沿[12]。

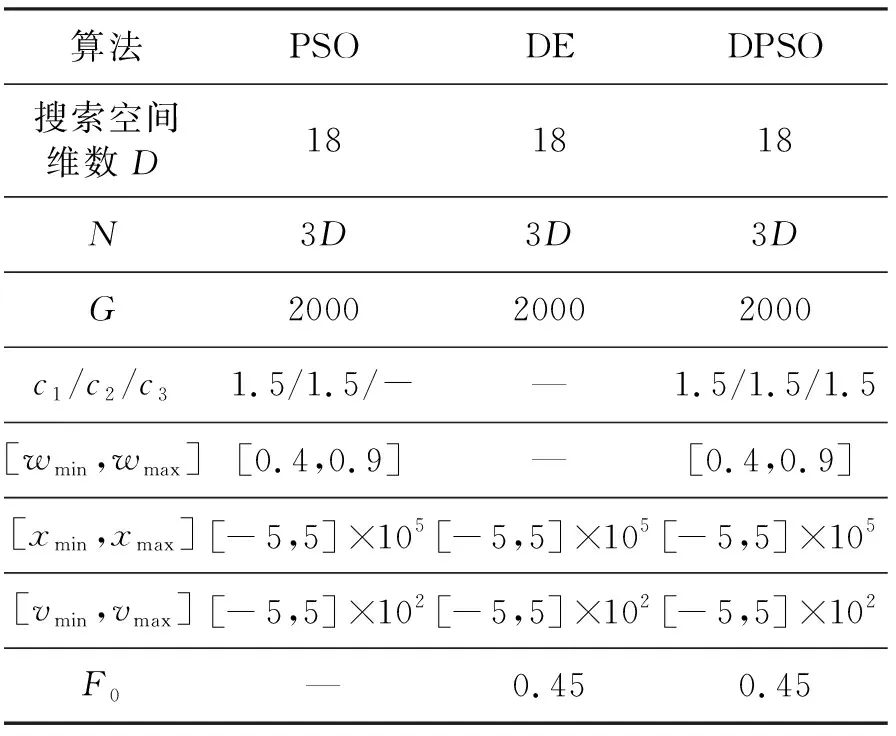
表1 三种算法下参数设置

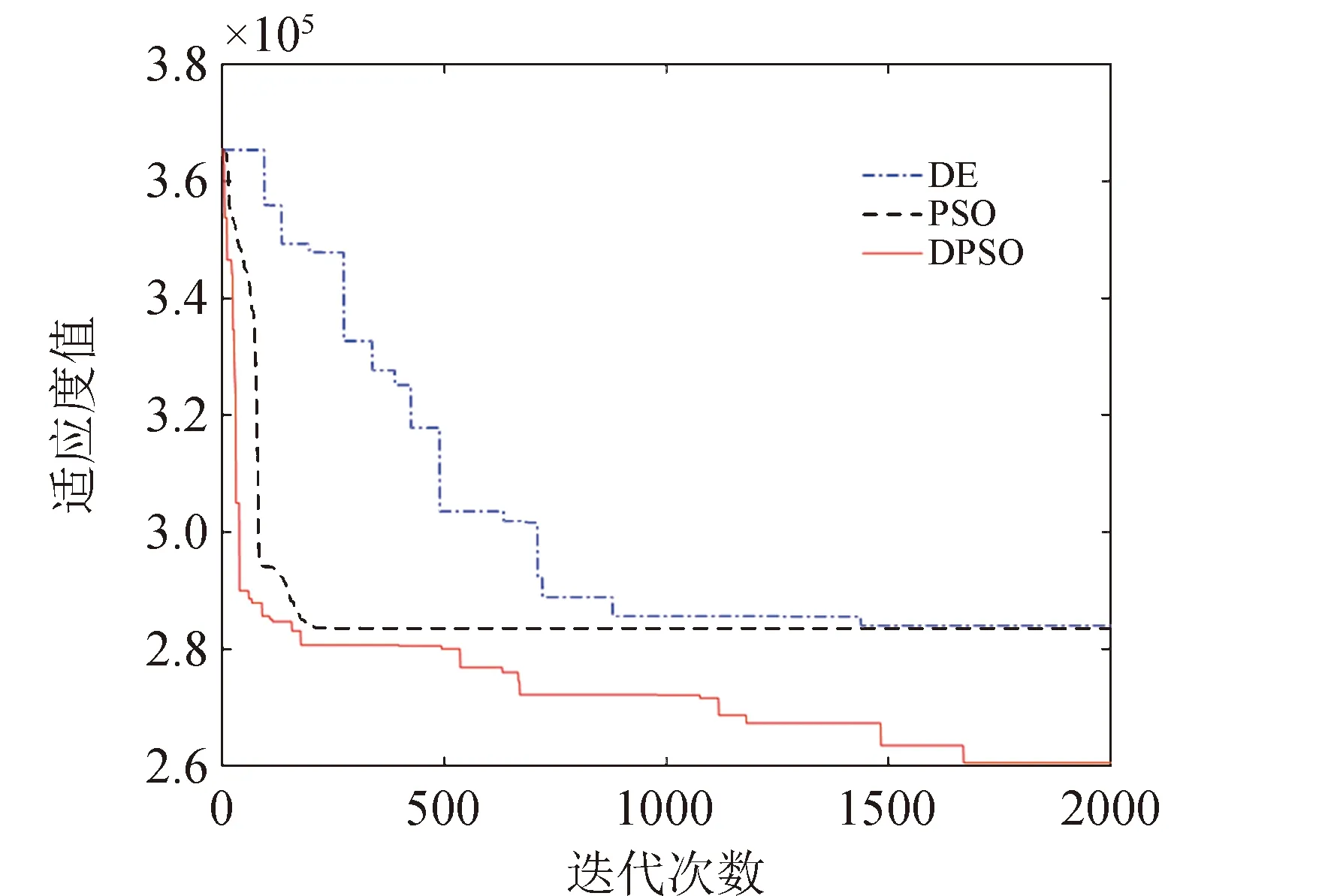
图4 三种算法下进化曲线Fig.4 Evolution curve under three algorithms

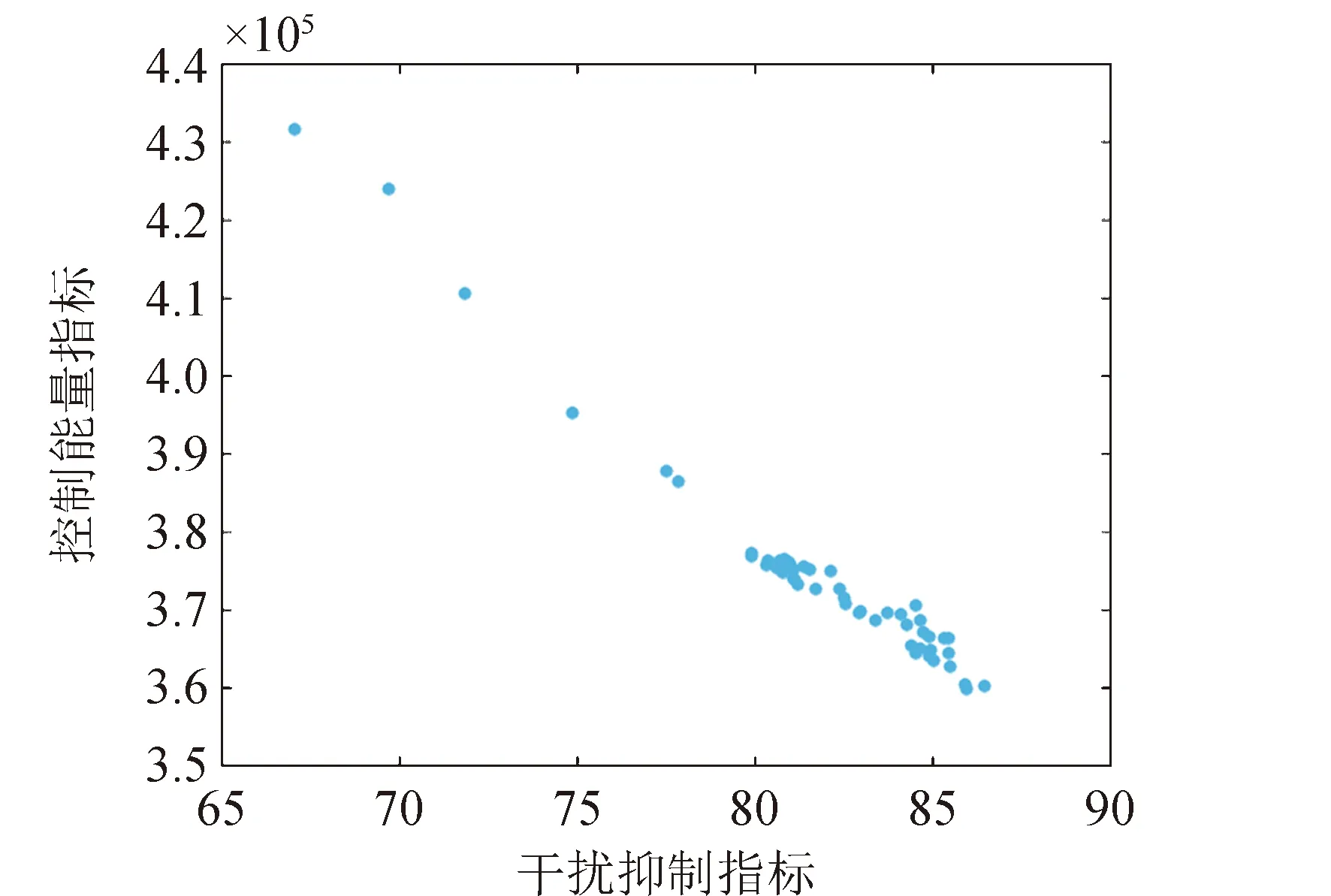
图5 外部解集Fig.5 Set of external solutions

为验证本文控制器的鲁棒性能、干扰抑制能力和控制能量优化效果，仿真时不妨取转动惯量(不同于J)和外部干扰为：

图8所示为三轴姿态受到的干扰作用，图9～图11为闭环系统仿真结果。由图9知航天器姿态稳定时间相对于PID控制减小，基本不超过100 s；在300 s后，PID控制姿态误差在1.35×10-4(°)以内，而本文方法下姿态误差在6.2×10-5(°)以内，减小了约54%，说明对干扰进行了有效抑制；图10显示在本文仿真算例下，两种方法控制力矩相差不大，本文方法控制力矩峰值约为6.99N·m，PID控制峰值约为8.42N·m；由图11知，本文控制方法下的航天器前两阶挠性模态振动幅度与PID控制相当，且处于较小的量级，其中与姿态耦合作用较强的第一阶挠性模态振动衰减更快，在100 s左右接近稳定(比PID快约250 s)。综上，本文方法对航天器高精度高稳定度鲁棒姿态控制具有良好的效果。

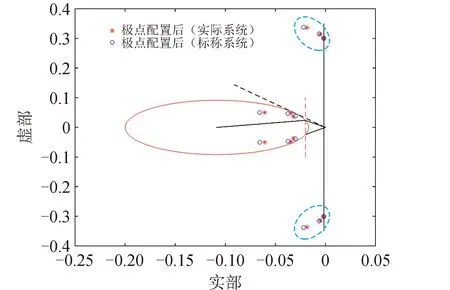
图 6 极点配置结果(图中线条与图2对应)Fig.6 Result of pole assignment

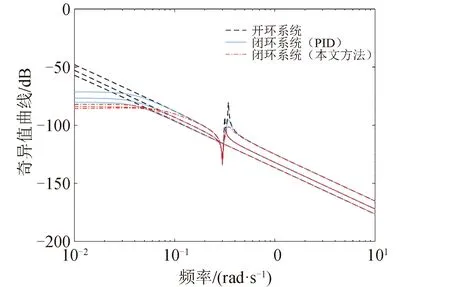
图7 开闭环系统奇异值曲线Fig.7 Singular value of open-loop and closed-loop system

图8 姿态干扰Fig.8 Attitude interference

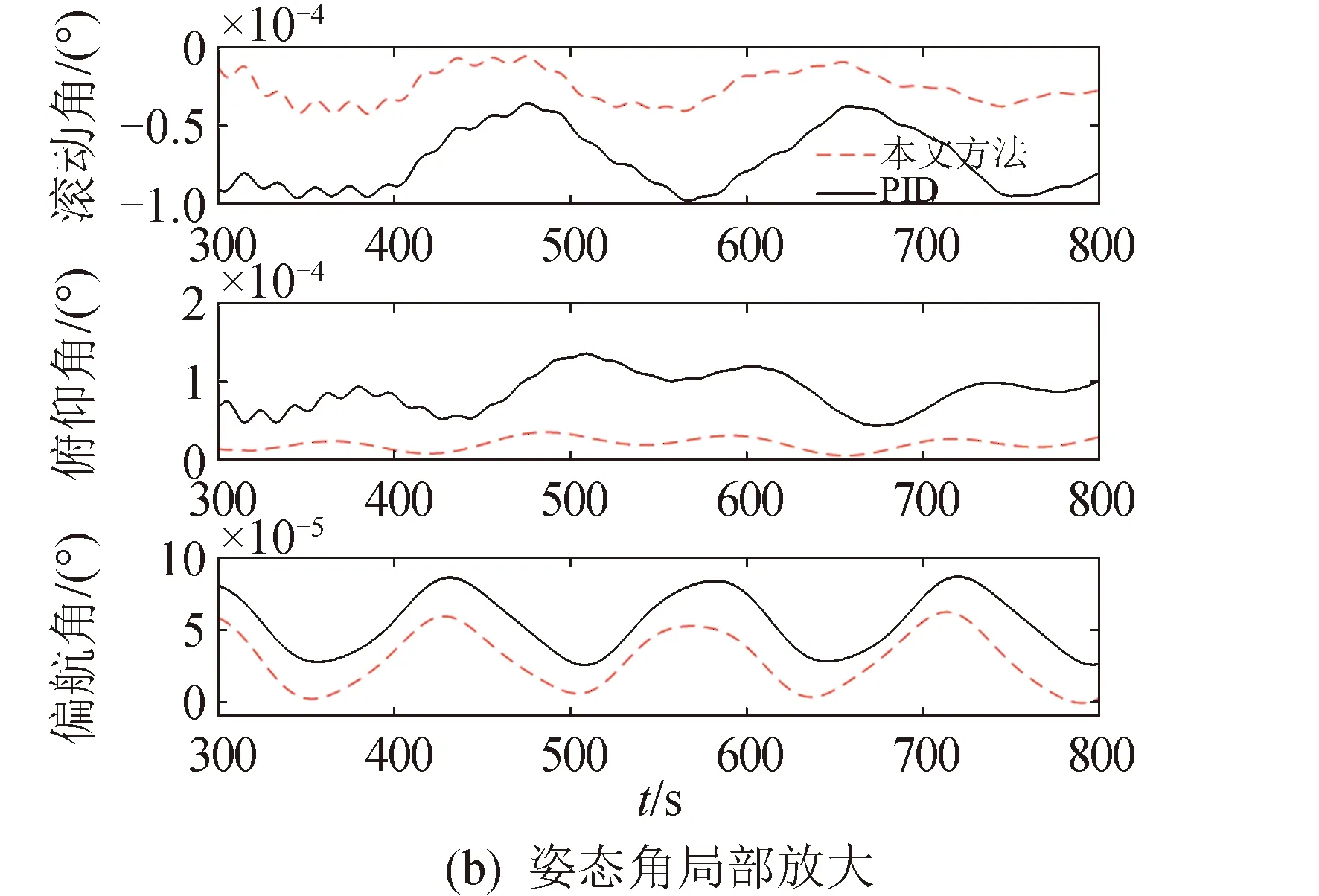
图9 姿态角Fig.9 Attitude angle

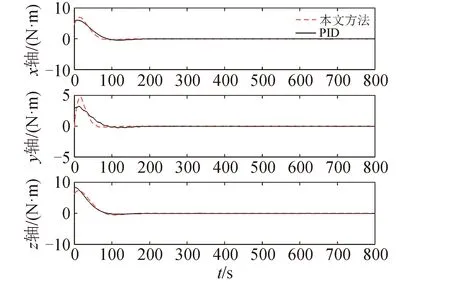
图10 控制力矩Fig10 Control torque

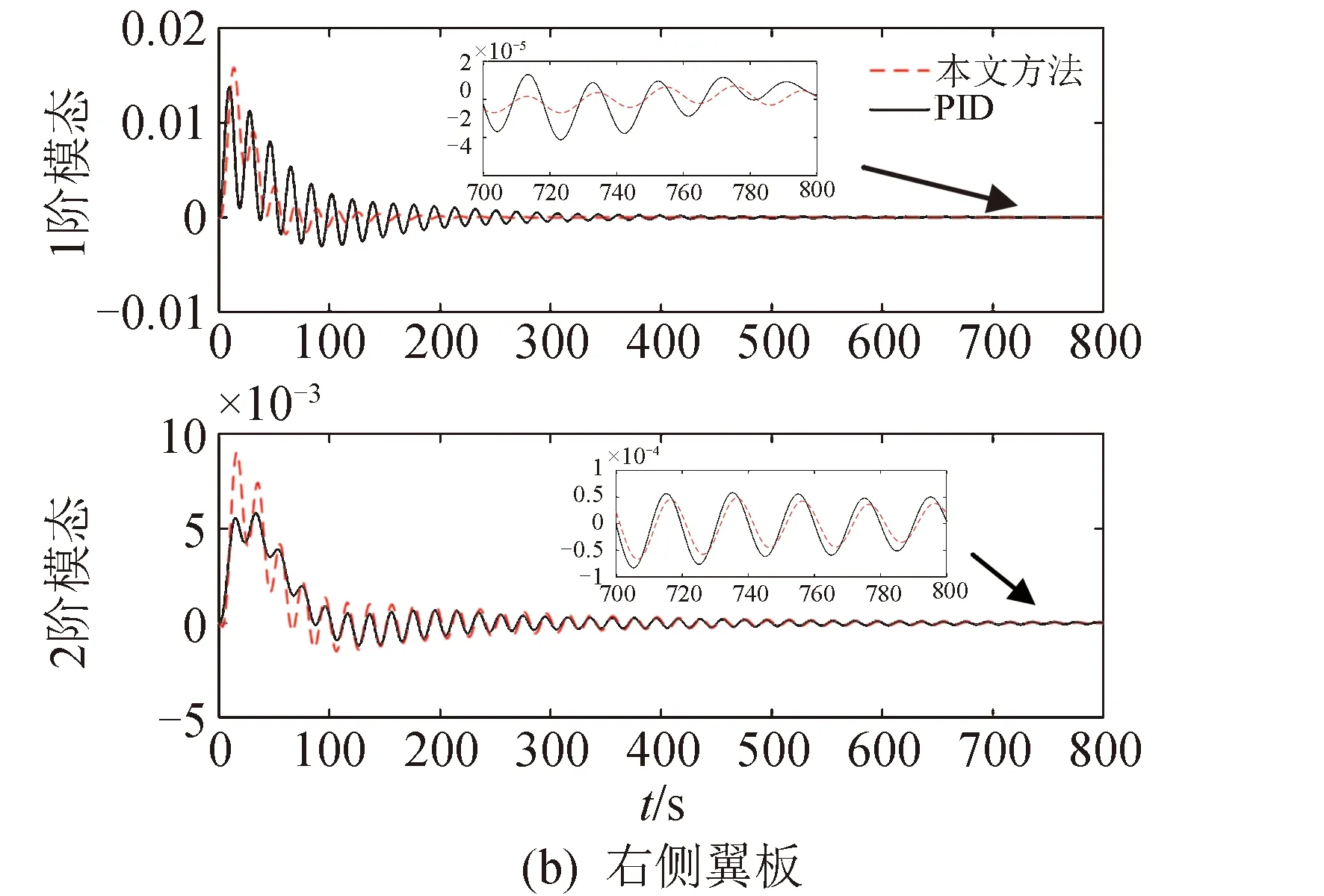
图11 挠性模态位移Fig.11 Flexible modal displacement

4 结束语

本文针对大型挠性航天器的高精度高稳定度姿态控制问题，将改进智能算法、现代控制理论和多目标Pareto最优思想结合，提出一种基于输出反馈和DPSO算法的多目标鲁棒控制器设计方法，并推导了含转动惯量不确定性的系统模型和鲁棒D-稳定的LMI表达。主要结论如下：

1)相较于DE算法和PSO算法，本文提出的DPSO算法寻优效果更好。在鲁棒区域极点约束下，利用DPSO算法和Pareto最优原则，对控制能量和鲁棒性能进行优化得到的控制器实现了闭环系统的鲁棒D-稳定，且起到了一定的振动抑制作用。

2)仿真验证了本文方法的有效性。在本算例中，相对于PID控制，本文方法下系统响应速度较快，其中第1阶挠性模态振动衰减时间减少约250 s，控制力矩峰值减小约1.43N·m，姿态稳态误差减小约54%。

3)将智能优化与现代控制理论结合，涉及的数学公式和参数较少，灵活性较强。本文方法弥补了经典PID控制在不确定系统模型下鲁棒性能以及抗干扰能力的不足；减小了带极点配置的LMI方法在多指标约束凸优化问题中的求解保守性；也能避免传统方法将多目标转化为加权指标函数时，由于多目标关系难以确定而导致的加权系数选择困难。

4)本文智能优化方法还可应用到更多复杂以及非线性系统控制参数优化问题上，为大型挠性航天器鲁棒控制器设计提供一种思路。