2-SGCMGs与磁力矩器的对地姿态混合控制方法

雷拥军，袁利,*，刘其睿，刘洁

1. 北京控制工程研究所，北京 100094 2. 空间智能控制技术重点实验室，北京 100094

控制力矩陀螺(CMG)系统可实现连续大力矩输出，满足角动量需求，是大型空间站、快速姿态机动航天器理想的执行机构，在航天器中得到广泛应用[1-7]。

鉴于航天器三轴姿态控制与奇异规避双重需求，大多数相关研究及系统设计一般采用不少于4台单框架控制力矩陀螺(SGCMG)配置方式[3, 5 -7]。姿态机动时CMG提供相应机动力矩，其高速转子轴系径向相应频繁偏载可能使得机械轴承润滑不良，从而导致部件失效故障[4,8]。当故障过程中剩下3台SGCMG可工作时，系统成为非冗余配置，针对该状态CMG系统的操纵问题已引起相关研究者的关注，并开展了相关探索性研究[9-11]。Thieuw等为Pleiades卫星所提出的4SGCMGs操纵律可兼容系统非冗余配置情况[6]。当故障过程中仅2台SGCMG可工作时，系统则褪化为欠驱动配置状态。

对于刚体运动的欠驱动控制问题，已有大量文献在理论与控制方法上开展了相关研究[12-17]。由于欠驱动姿态控制系统不满足Brockett必要条件，无法通过光滑反馈控制实现系统的渐近稳定[12]，因此现有控制方法研究通过引入时变控制律、多控制律切换等非光滑控制策略来解决该问题[13-16]。然而，针对角动量交换形式的航天器姿态欠驱动控制，一般需满足系统总角动量为零的条件。Crouch 分析给出了在1～3个独立控制力矩下刚体可控充要条件，并指出对于角动量交换控制系统，当控制自由度少于3时，系统可控性是无法保证的[17-18]。在实际工程中，由于航天器系统难免受到空间环境力矩作用影响，采用CMG角动量交换控制方式的系统很难保证系统总角动量为零状态，因而现有欠驱动控制方法在实际应用中一般难以保证系统鲁棒稳定性。对于系统总角动量非零情况，当该角动量位于星体系下特定面内区域时可实现轮系欠驱动航天器的指向稳定控制[19]，然而对地稳定运行航天器的非零总角动量在星体系下的方向将随星体在惯性系下大范围指向运动变化而变化，从而无法满足始终位于特定区域的条件，这使得欠驱动控制方法在长期对地稳定运行航天器实际应用上变得更加困难。

磁力矩器是中、低轨道卫星的基本配置执行机构[20-23]，除了用于小卫星姿态磁控外，主要作为空间环境扰动力矩产生的累积角动量的重要卸载手段。小卫星采用磁控可实现星体对地三轴稳定控制[23]，但其高达几度量级的姿态控制误差使其仅适用于控制精度要求不高的对象。虽然磁力矩器产生的力矩量级较小，但是在欠配置系统的姿态控制中将其引入姿态控制，不失为一种提升系统控制能力及鲁棒性的技术途径。

针对上述2-SGCMGs非完整配置系统长期对地高精度稳定运行的控制问题，本文设计了一种2-SGCMGs与磁力矩器组合的卫星控制方法，以解决发生故障时仅余2个控制力矩陀螺可用时的系统控制问题。首先，根据非平行的SGCMG的低速框架轴单位向量，求解两SGCMG合成角动量为零所对应的标称框架角；其次，根据标称框架角构型，构造新的控制标架，将三维控制力矩指令空间分解为分别由SGCMG与磁力矩器来实现的两正交子空间；最后，根据不同子空间的控制指令，给出SGCMG框架角速度指令与考虑磁卸载的磁力矩器控制磁矩求解表达式；最后，针对所提出的方法，结合航天器对象进行相应的数学仿真验证。

1 2-SGCMGs标称框架位置的选择

由两单框架控制力矩陀螺所组成的系统，若CMG低速框架轴单位向量g1、g2不平行，随其框架转动时其角动量h1与h2分别在与各框架轴垂直的平面内运动，如图1所示。

图1 2-SGCMGs系统的角动量随框架运动变化示意Fig.1 Schematic representation of momentum variations for a 2-SGCMGs system

假定各CMG角动量幅值均相同且为h，当框架角为δi(i=1,2)时CMG在星体系下的角动量hi可表示为：

hi(δi)=h·(Misinδi+Nicosδi)

(1)

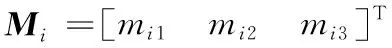
记框架角组合δ=[δ1,δ2]Τ，由式(1)可得CMG系统在星体下合成角动量Hcmg为：

(2)

对于角动量管理装置作为执行机构的对地稳定卫星，控制主要为零角动量及偏置角动量两种方式，其中后者在星体-Y轴有一定角动量偏置以提供系统稳定性。对于2-SGCMGs系统指定的角动量，由式(2)可解得对应的框架角。由于该式具有三角函数方程，比较复杂，故仅考虑2-SGCMGs的零动量控制方式，并给出对应的几何求解方法。

当系统合成角动量为零时，由图1所示几何关系可知，每个CMG角动量均与两角动量运动平面交线AB平行，即h1∥h2∥(g1×g2)且h1=-h2，不妨记在零角动量下两CMG的角动量单位向量为h01与h02，选取

h01=-h02=g1×g2/‖g1×g2‖

(3)

或

h01=-h02=-g1×g2/‖g1×g2‖

(4)

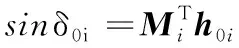
2 SGCMG与磁力矩器的混合控制

2.1 对地姿态稳定控制器设计

卫星本体坐标系相对轨道坐标系的姿态四元数q和角速度ωbo描述的卫星姿态运动为：

(5)

式中：qv与q4分别为q的矢量部分与标量部分。

考虑控制力矩陀螺的刚体卫星姿态动力学方程为：

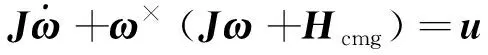
(6)

式中：J为星体转动惯量；u为施加星体力矩向量；ω为星体相对惯性系的角速度。

考虑关系式

其中：Cbo为星体坐标系相对轨道坐标系的方向余弦阵；ωo为轨道角速率，对于近圆轨道可近似看为常数。

对式(5)与式(6)组成的系统，采用如下形式PD控制：

u=-kpqv-kdωbo+

(7)

式中：kp、kd均为正定矩阵。

对

对V求时间导数并整理有

并由拉萨尔不变集原理可知，在式(7)控制作用下可使得在无外扰下闭环系统具有渐近稳定特性，其中qv→0，ωbo→0。

根据框架运动学可知，每个控制力矩陀螺输出力矩为：

对于两单框架控制力矩陀螺与磁力矩器混合控制，定义控制框架为：

(8)

由于CMG输出力矩幅值远远大于磁力矩器产生的力矩，因此系数阵kp与kd除了满足正定性条件外，还需要兼顾两种不同类型执行机构的有效力矩输出量级。对于式(7)中的控制参数矩阵kp、kd，将其表示为如下形式：

则式(7)中的PD控制部分可表示为：

即有

(9)

2.2 混合执行机构控制力矩实现

记框架角组合δ=[δ1,δ2]Τ，式(2)可表示为：

Hcmg(δ)=h(Msinδ+Ncosδ)I2×1

(10)

对Hcmg(δ)求时间导数可得：

(11)

由式(11)关系可得其与CMG框架转速指令满足关系式

可得：

(12)

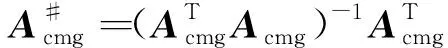
在空间环境力矩的作用下，角动量积累将导致CMG框架角偏离其标称位置。由于两CMG角动量仅能在各自的固定平面内运动，因此该系统无法完全容纳三维空间中的角动量积累，随卫星绕地球进行对地指向运动中势必产生较大的姿态偏差，且该偏差方向随时间而改变，因此磁力矩器除产生单自由度方向控制力矩外，还得对角动量进行有效卸载。

由式(2)，在δ=δ0处线性化，可得CMG系统角动量偏差为：

式中：Δδi=δi-Δδ0i。

设计角动量卸载律为：

uunload=-kpΔHcmg(δ)|δ=δ0-

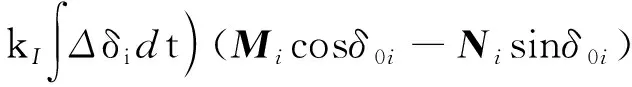
(13)

式中：uunload为期望的角动量卸载力矩；卸载控制参数kp、kI≥0。

综合姿态控制及磁卸载，磁力矩器产生的期望控制力矩为：

uΣMT=uMT+uunload

由磁力矩器与空间磁场作用产生力矩的原理，可得其磁矩指令为：

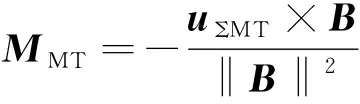
(14)

式中：B为地磁场强度矢量在星体下的表示。

对由式(14)所得到的MMT，由该磁矩指令产生的力矩τMT=MMT×B，可得

(15)

由此可知，若uΣMT与B非正交，则产生额外的非期望力矩，其对星体姿态会造成一定程度扰动。

3 数学仿真校验

针对给出的2-SGCMGs与磁力矩姿态混合控制算法进行仿真验证。仿真对象为运行于轨道高度490 km的太阳同步轨道的刚体卫星，对应轨道角速率为ωo= 0.001 01 rad·s-1，星体转动惯量为：

系统配置两CMG的角动量幅值均25N·m·s，其框架轴单位向量分别为：

对应安装参数向量为：

由以上参数可得：

h01=-h02=

进而由式(3)(4)计算得到2-SGCMGs系统组成零角动量的标称框架角分别为29.79°与150.21°。

控制参数选取

在星体滚动与俯仰方向设定常值空间环境力矩分别为2×10-4与5×10-4N·m，配置磁力矩器输出最大磁矩幅值为100A·m2。磁卸载系数选取为:

kp=4×10-4，kI=2×10-5

仿真历经10 000 s，近两轨道周期，仿真结果如图2～图6所示。由图2与图3中星体系相对轨道系的欧拉姿态角及欧拉角速度可以看出，在两CMG与磁力矩器联合控制下系统很快消除1°初始姿态偏差进入稳态，进入稳态后三轴姿态角误差小于0.02°，角速度误差小于0.000 1°/s，可满足高精度遥感卫星0.000 5°/s姿态稳定度要求[24]；在磁力矩器卸载作用下，图4中CMG低速框架角保持在标称值附近；结合姿态控制效果及图5中CMG框架角速度与图6中磁力矩在星体系下产生磁矩，反映了控制力矩指令空间分解及两类执行机构分配力矩实现策略的正确性及有效性；图6中磁力矩器在稳态控制时产生最大磁矩幅值约为25A·m2，对于设定量级外界扰动还有较大的裕度。

为验证系统抗外扰鲁棒性，在维持上述配置及参数不变情况下增大外扰力矩。外扰力矩沿星体三轴分别设定为0.001 5sin(2ωot)、0.001与0.001sin(ωot) N·m，高于一般同类轨道高度航天器环境扰动力矩10-4N·m量级[25]，对应仿真结果如图7～图11所示。

图2 欧拉姿态角Fig.2 Euler angle

图3 欧拉角速度Fig.3 Derivatives of Euler angle

图4 CMG框架角Fig.4 Gimbal angle of CMGs

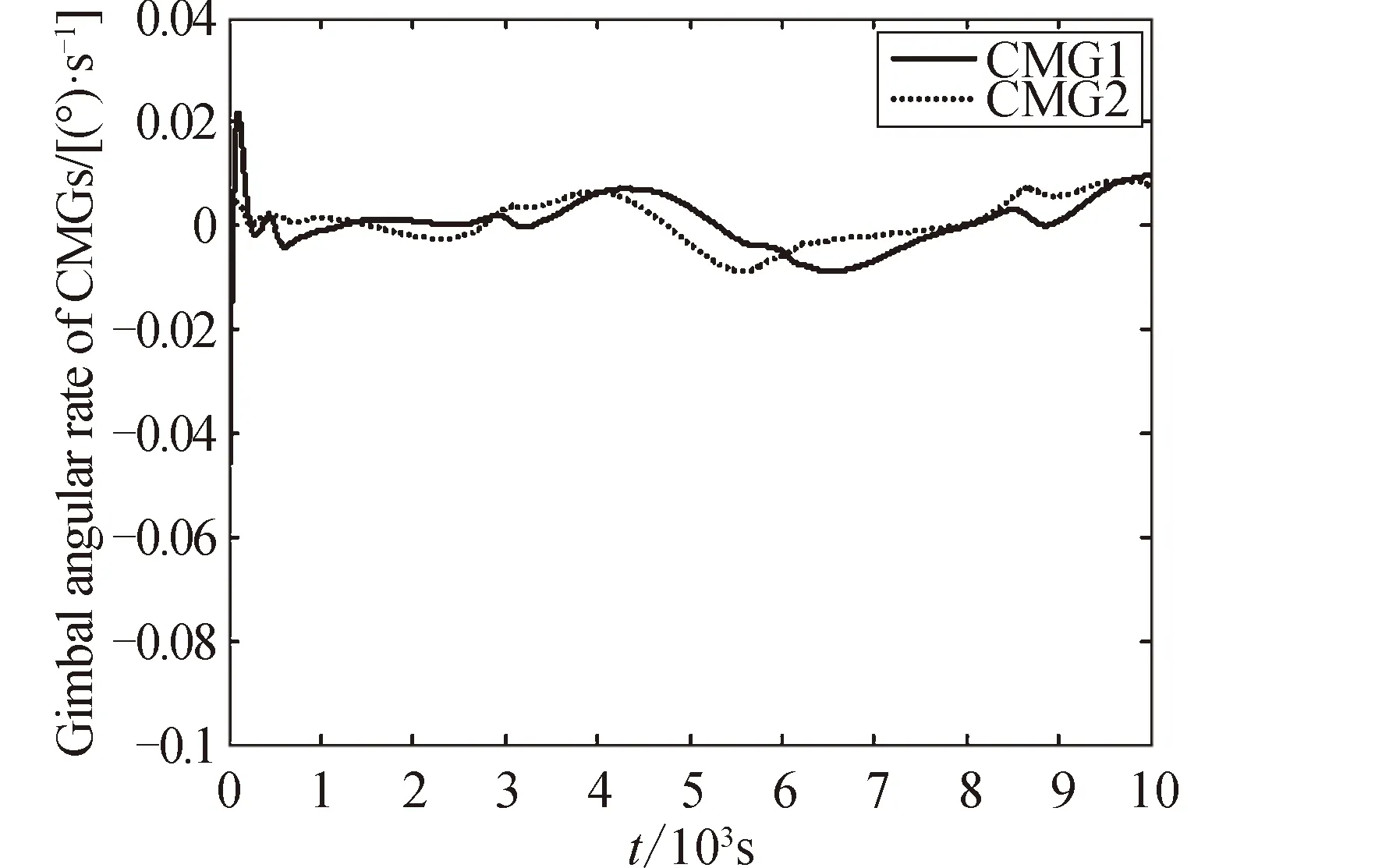
图5 CMG框架角速度Fig.5 Gimbal angular rate of CMGs

图6 磁力矩器产生的磁矩Fig.6 Magnetic dipole moment

图7 系统大扰动下的欧拉姿态角Fig.7 Euler angle of the system in the case of large disturbances

图8 系统大扰动下的欧拉角速度Fig.8 Derivatives of Euler angles of the system in the case of large disturbances

由图7中姿态及图8中姿态角速度曲线可知，稳态过程中姿态误差小于0.05°，角速度波动量小于0.000 5°/s，相比前述仿真结果有所增加；由图9及图10执行机构控制输出可知，由于外扰增大使得CMG框架角速度与磁力矩器磁矩均相应增大。由于设定外扰超过磁力矩器控制及卸载能力使得在5 000～6 000 s时间段磁矩饱和，在实际系统设计中可针对外扰量级选择合适磁矩输出能力的磁力矩器。

由图11可知：CMG合成角动量，即磁卸载残余角动量，沿星体三轴方向均在2N·m·s范围内波动。由式(15)可知，除沿特定方向外，磁力矩器无法产生与外扰完全相抵消的力矩，故角动量磁卸载为一段较长时间内的综合作用效果，无法保证任意时刻残余角动量均为零。在无CMG系统对该残余角动量容纳情况下，由角动量守恒与对象转动惯量计算得知其可引起幅值高达0.03°/s的星体角速度。由图2中姿态角速度可见，在CMG与磁力矩器联合参与控制下，其对角速度影响在星体三轴方向均降低近两个数量级，从而反应了本文所提出混合控制方法的鲁棒性与相对纯磁控的高品质性能。

图9 系统大扰动下的CMG框架角速度Fig.9 CMG Gimbal angular rate of the system in the case of large disturbances

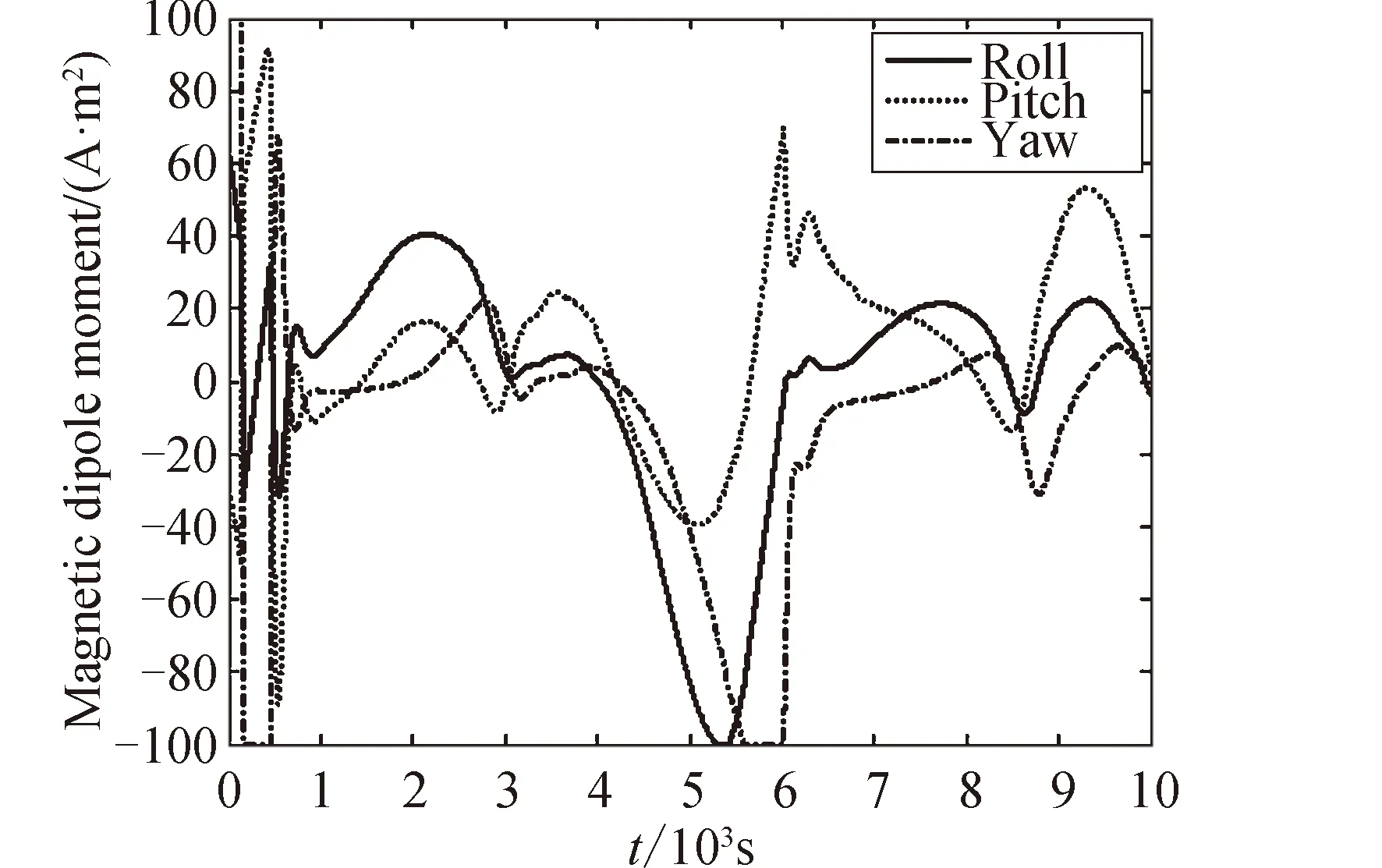
图10 系统大扰动下的磁力矩器磁矩Fig.10 Magnetic dipole moment of the system in the case of large disturbances

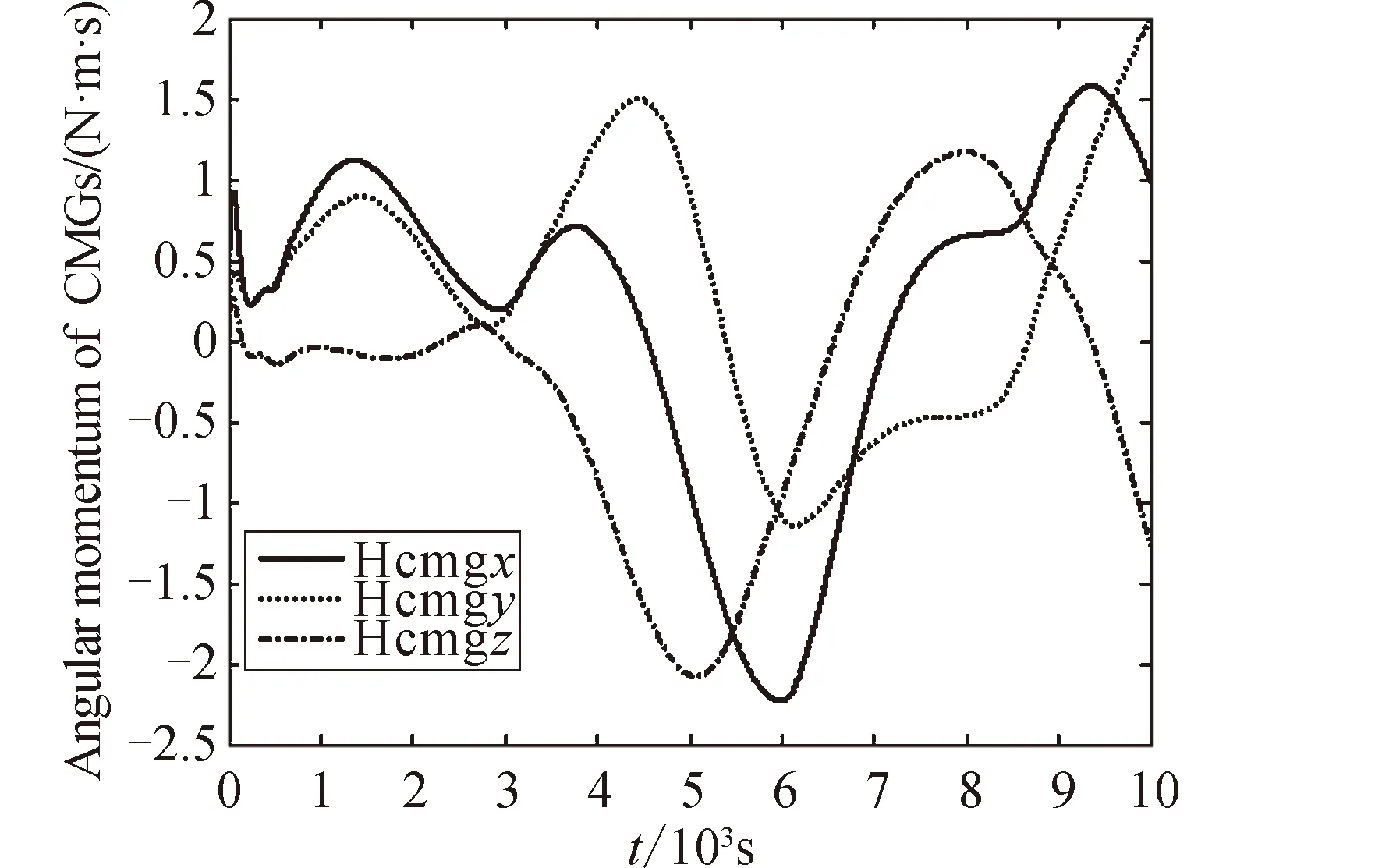
图11 两CMG合成角动量Fig.11 Total angular momentum of 2 CMGs

4 结束语

对于空间环境干扰下保持对地长期稳定运行的2-SGCMGs航天器系统，设计了一种控制力矩陀螺与磁力矩器组合的混合控制方法，解决在控制力矩陀螺发生故障的情况下，仅余2个陀螺可用时的系统控制问题，达到充分延长卫星使用寿命的目的。通过分析与仿真验证可得到如下结论：

1)根据标称框架角构型，构造新的控制标架，从而实现将三维控制力矩指令空间分解为分别由SGCMG与磁力矩器来实现的两正交子空间，为双SGCMG与磁力矩器组合的混合控制系统设计提供了有利的条件。

2)根据不同子空间的控制指令，给出了SGCMG框架角速度指令及包含磁卸载在内的磁力矩器控制磁矩求解实现。

3)通过空间环境扰动下的数学仿真验证，表明所提出方法可以保证系统良好控制性能且对外界干扰具有较强的鲁棒性，实现了姿态误差小于0.05°且稳定度优于0.000 5°/s的控制性能，可满足一般高精度对地遥感卫星控制需求。

4)所提出方法仅解决了对地定向卫星三轴稳定控制问题，为了提高观测效率，实现星下点非沿迹成像，针对对地姿态重定位机动过程的控制问题，还有待与2-SGCMGs系统欠驱动控制方法相结合做进一步研究。

本文所提出的方法充分挖掘了现有航天器执行机构配置潜能，实现了两SGCMG和磁力矩器进行姿态混合控制，克服了欠2-SGCMG系统欠驱动的鲁棒性问题与全磁控姿态精度不高的问题，提升了卫星故障容错能力，有效提高了2-SGCMGs欠配置下卫星控制的鲁棒性。