基于在轨温度测量数据的整星结构尺寸稳定性分析
2021-03-16罗文波张新伟钱志英张玲白刚莫凡卢青荣殷亚州傅伟纯
罗文波,张新伟,钱志英,张玲,白刚,莫凡,卢青荣,殷亚州,傅伟纯
1. 北京空间飞行器总体设计部,北京 100094 2. 北京控制工程研究所,北京 100094
高分七号卫星是我国首颗亚微米级高分辨率光学传输型立体测绘卫星,已于2019年11月3日发射成功。到目前为止,已经回传大量高精度测绘数据,卫星功能正常,性能满足设计指标要求。高分七号卫星配置双线阵相机和2束激光测高仪载荷,能够获取高空间分辨率立体测绘遥感数据和高精度激光测高数据。由于双线阵相机、激光测高仪和星敏之间需要配合使用,除成像载荷本身的测量精度外,卫星结构的在轨尺寸稳定性也是影响卫星图像定位精度的重要因素之一。本文依据在轨温度场遥测数据,结合热分析结果,建立了基于实测数据的温度场反演方法,并开展了尺寸稳定性的分析工作。
基于在轨热分析温度场计算航天器在轨热变形,已经是较为成熟的分析技术,在国内外高精度遥感和科学探测卫星中得到广泛的应用。游思梁等利用直接计算获得的温度场计算天线在轨热变形[1]。Stephen M Merkowitz等人针对LISA卫星开展了光机热建模与分析[2],其中热变形分析的温度场通过I-IDEAS软件仿真得到。在欧空局(ESA)的载荷设计手册中[3],提到了由热分析软件到结构分析软件的温度场映射方法。刘振宇等人[4]利用I-DEAS软件分析的在轨温度场,完成了变工况空间太阳电池翼在轨热变形分析。左博等利用数据文件转换的方式实现温度场的赋值和热变形计算[5]。刘国青等人[6-7]实现了航天器在轨全周期热变形分析。但以上分析都是基于热分析温度场得出,鲜有利用在轨温度测量数据反演结构温度场,进而对结构稳定性指标进行预示分析的报道。针对温度数据反演,丁鹏[8]对飞行器再入热控试验中的热源进行了估计;张庆建立了与IDEAS的TMG模块的转换接口[9];潘腾、张也驰等人[10-11]提出了利用普通克里格法依据温度实测点进行插值并以此计算了载荷在地面热真空试验中的结构热变形;帅永[12]等采用自适应算法和加权算法求解航天器热平衡试验中多热源非线性温度场反演问题。此外,在其他领域,周晓敏等[13]在地质领域也开展了相关的研究;霍海娥[14]进行了边界温度的反演研究;娄继琳采用神经网络的方法对电子器件内的温度场进行了推算[15]。但目前方法均建立在较多的温度测量数据基础上。本文利用星上有限测点的温度测量数据,以热分析温度场为基础,建立了一种基于模型和在轨测量数据的温度场反演方法,实现了卫星结构在轨温度场的反演,并利用反演温度场,给出了基于在轨监测数据的结构稳定性指标分析。
1 结构尺寸稳定性设计指标
高分七号卫星作为高精度测绘卫星,为了得到同名点在不同图像中的位置以匹配成立体图像,需要图像具有较高的定位精度和图像质量。除了载荷自身的尺寸稳定性外,还要求相机之间、相机与激光测高仪之间也有较高的稳定性。相机与激光测高仪均安装在卫星的一体化支架上,一体化支架以及其他结构的热变形,将直接影响各个相机之间的夹角稳定性,因此相机与激光测高仪之间的尺寸稳定性需要通过卫星结构的热变形的尺寸稳定性来保证。高分七号构型及各个相机位置见图1。
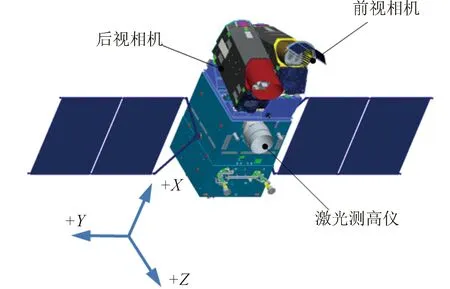
图1 高分七号卫星组成Fig.1 Configuration of GF-7 satellite
根据载荷工作模式及在轨标定情况,结构在轨尺寸稳定性要求分为短期稳定性和长期稳定性[16],定义如下:
1)短期稳定性:一次成像期间的稳定性。
2)长期稳定性:一次标定期内对同一区域成像的稳定性。
整星结构在轨尺寸稳定性指标定义为前视相机、后视相机和激光测高仪安装面在整星坐标系XOZ平面内相对夹角变化,短期(10 min)稳定性要求不大于0.6″,长期稳定性(一个标定期内)要求不大于1.5″。
2 在轨温度数据分析
为研究整星结构在轨温度遥测数据的变化规律,对高分七号正式入轨工作早期1个月 (2019年11月13日11时03分0秒至2019年12月15日0时22分0秒)的474轨温度测量数据开展了数据挖掘分析。为研究整星结构在轨温度遥测数据的频域特性,对在轨温度数据进行了频谱分析。图2是某典型测点温度遥测数据的傅里叶幅值谱。通过频谱分析可知,一个轨道周期为5 679.88 s(约1.58 h,对应频率为0.000 176 Hz)。根据太阳同步轨道卫星的外热流特点,选取卫星具有代表性的结构板上的温度进行了分析。从温度遥测数据的频域分析数据可以看出,数据的主要频率成分是轨道周期的1倍频,其次是轨道周期的2倍频。

图2 卫星典型位置温度测点遥测数据傅里叶幅值谱Fig.2 Fourier amplidute specturm of the in-orbit temperature data on the typical ponits in satellite
3 在轨温度场反演与映射
由于星上资源有限,温度测点在结构上的布局较为稀疏,个别结构板上只有一个测点。通过星上稀疏布置的测温点在轨测量数据,并结合整星热分析得到的整星温度场分布,通过数据外推反演出整星结构的温度场分布。由于在轨测量数据和热分析数据的采样时刻通常不同,在温度场反演前,需要对在轨遥测数据进行时间对准、差值和重采样。然后,将整星结构根据温度测点分布情况,划分为m个区域。假设结构部件上某个区域点的分析温度为Ti(i=1,2,…,n),且温度测点B的热分析温度为Tb,对应遥测温度为Tref,则该区域内的温度场可以描述为:
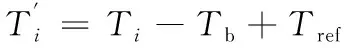
(1)
由于整星的温度场是以轨道周期的1倍频为主要频率成分的时域数据,因此,可以利用地面计算的1轨温度场数据为模板,在各个周期内,利用公式(1)反演得到各个结构部件的温度场分布。
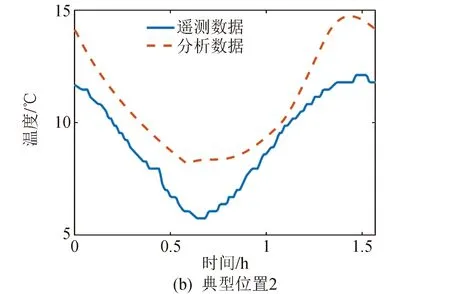
图3是3个典型位置遥测温度和计算温度的对比,从这些位置温度对比曲线可以看出,各个典型位置的温度在1个轨道周期内的变化规律是比较一致的,多数位置遥测温度和计算温度在不同时刻的温度场的数据差值并不大。实际上,公式(1)并不要求各个时刻的遥测和计算的温差相同,只要两者增减趋势相同,即可利用公式(1)进行以分析温度场为模板的温度场反演计算。

基于在轨温度测量数据得到反演温度场后,采用热传导映射方法,将在轨反演温度场映射到结构模型中。热传导法以既有节点温度场为基础,根据结构热传导特性映射其余部分的结构温度,从而避免了差值映射法中经常出现的空间距离较近但不属于同一结构件且温度差别较大的节点上出现的温度场映射误差问题。热传导法的差值方程为:

(2)
式中:Tf为结构节点温度矩阵;Ct为热传导矩阵;A为权重系数矩阵;Tt为热分析模型节点温度矩阵;q为拉格朗日乘子;上标f表示结构分析模型;上标t表示热分析模型;上标T表示转置。
4 稳定性指标分析
4.1载荷安装面法线夹角拟合计算方法
整星结构在轨尺寸稳定性指标定义为前视相机、后视相机和激光测高仪安装面在整星坐标系XOZ平面内相对夹角变化。变形分析采用有限元方法得到的直接结果是位移,因此需要将相机安装面的位移转化为其法线指向的变化。
设待拟合平面法线矢量的n个节点的坐标为(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn),写成如下形式的矩阵:
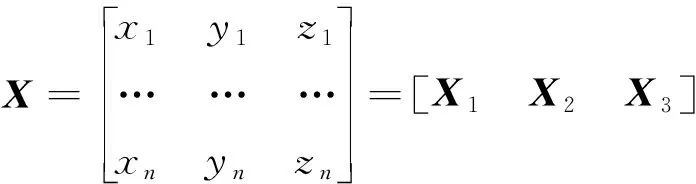
(3)
由式(3)各列减去各自的均值,得到如下矩阵:
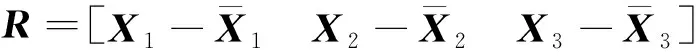
(4)
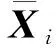
计算矩阵RTR的特征值和特征矢量,最小特征值对应的特征矢量即为拟合平面的法线矢量[17]。
假设载荷1安装面法线矢量为V1=[v1x,v1y,v1z],载荷2安装面法线矢量为V2=[v2x,v2y,v2z],则两个矢量在XOZ平面的投影矢量为V1XOZ=[v1x,0,v1z]和V2XOZ=[v2x,0,v2z],即可得到两个载荷安装面法线矢量在XOZ平面的投影夹角为:
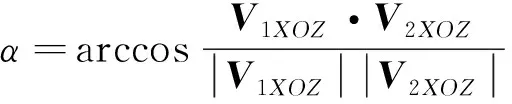
(5)
4.2 短期稳定性指标分析
根据稳定性指标定义,短期稳定性定义为一次成像期间的稳定性。针对卫星在轨工作1个月内的载荷安装面的短期尺寸稳定性分工况开展分析计算,并对计算结果进行统计分析。
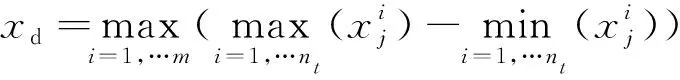
(6)
采用以上方法,分别计算了3种载荷工作模式下(分析工况定义见表1)的载荷安装面夹角短期稳定性,分析结果见图4。
针对以上短期稳定性预示结果,开展了统计分析,结果见表 2。从表2可以看出: 1)在寿命初期的1个月内,各载荷安装面短期稳定性指标分析最大值为0.4″,均满足不大于0.6″的指标要求;2)从均值统计来看,各载荷安装面短期稳定性均值在0.25″左右,其中工况2(即第58 min开始成像)稳定性均值最小。
由图4可以看出,各个工况下三个夹角的稳定性是随轨道数变化的,且变化的规律比较复杂。如果通过仿真的温度场来计算夹角稳定性,因为分析得到的温度场是近似周期性的,那么各个轨道上的夹角稳定性将近似是一条直线,无法得到图4中夹角的变化规律。这也说明,通过在轨遥测温度场计算的稳定性指标比利用仿真温度场得到的稳定性指标更真实,也更反映实际在轨状态。观察图4各个曲线的变化规律,还可以看出:在不同的轨道,大部分数据点是波动比较小的,只有个别的点波动比较大。因此,对各个数据的幅值分布进行了分析,结果如表3所示。

表1 结构稳定性分析工况定义
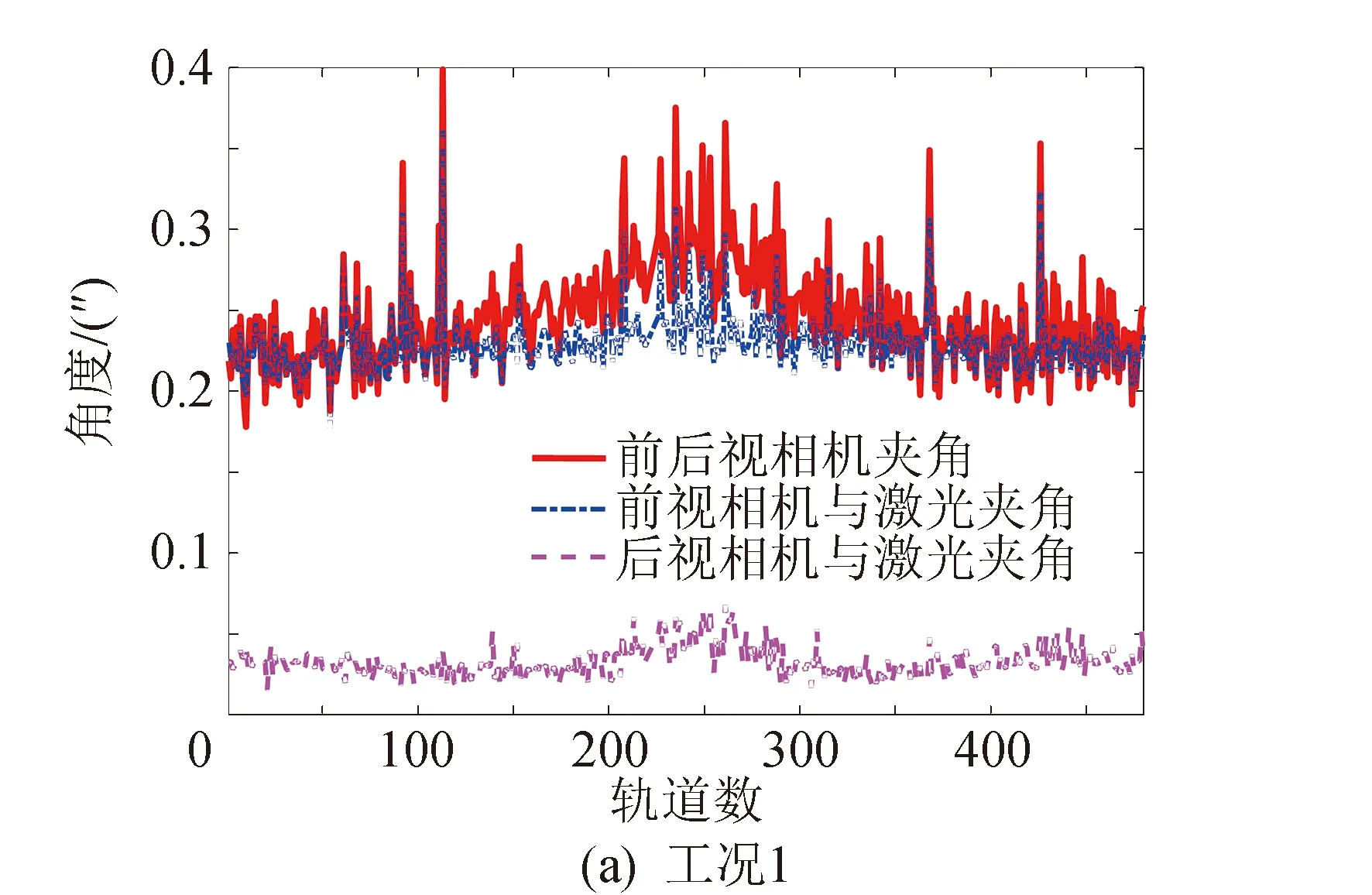
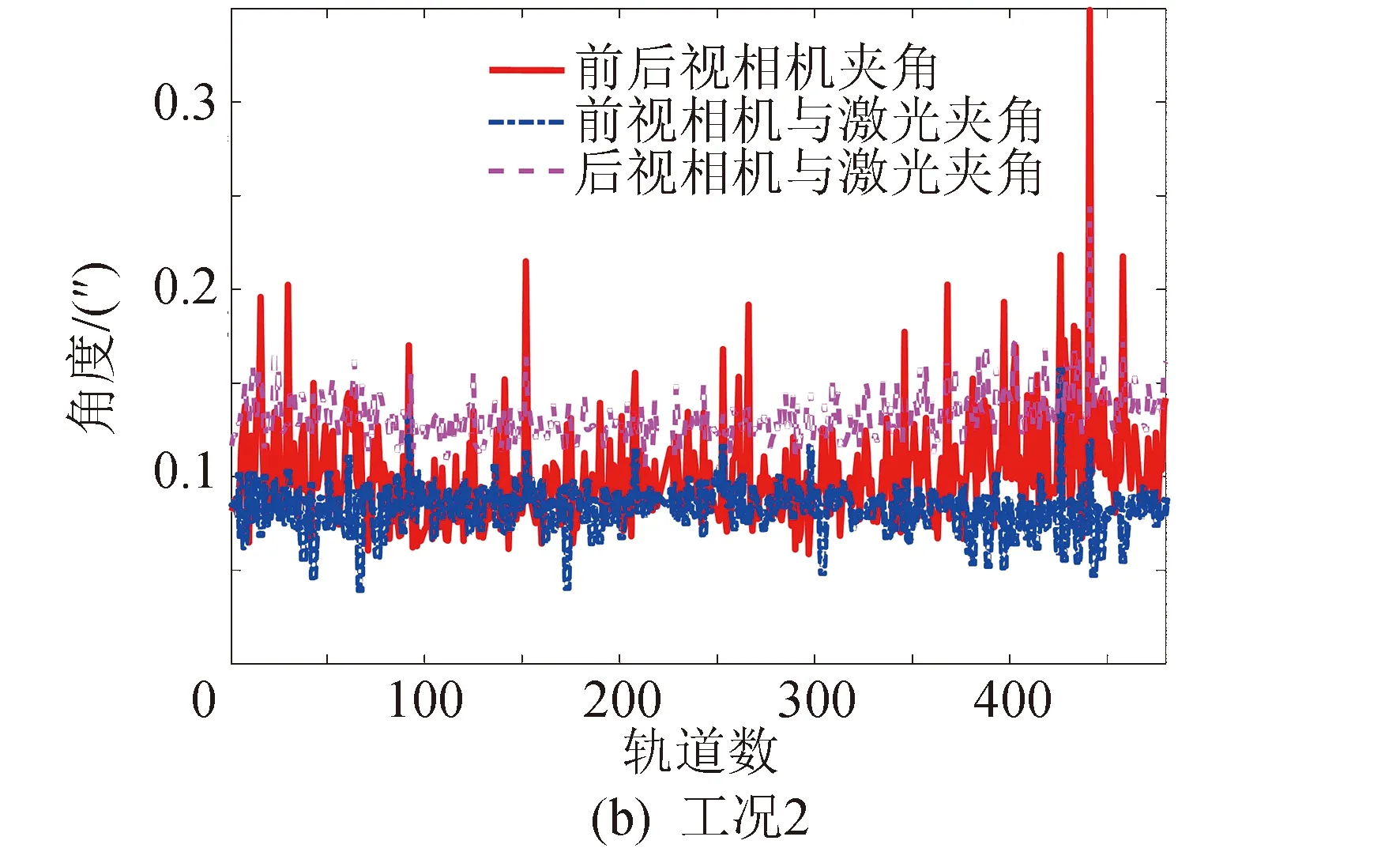
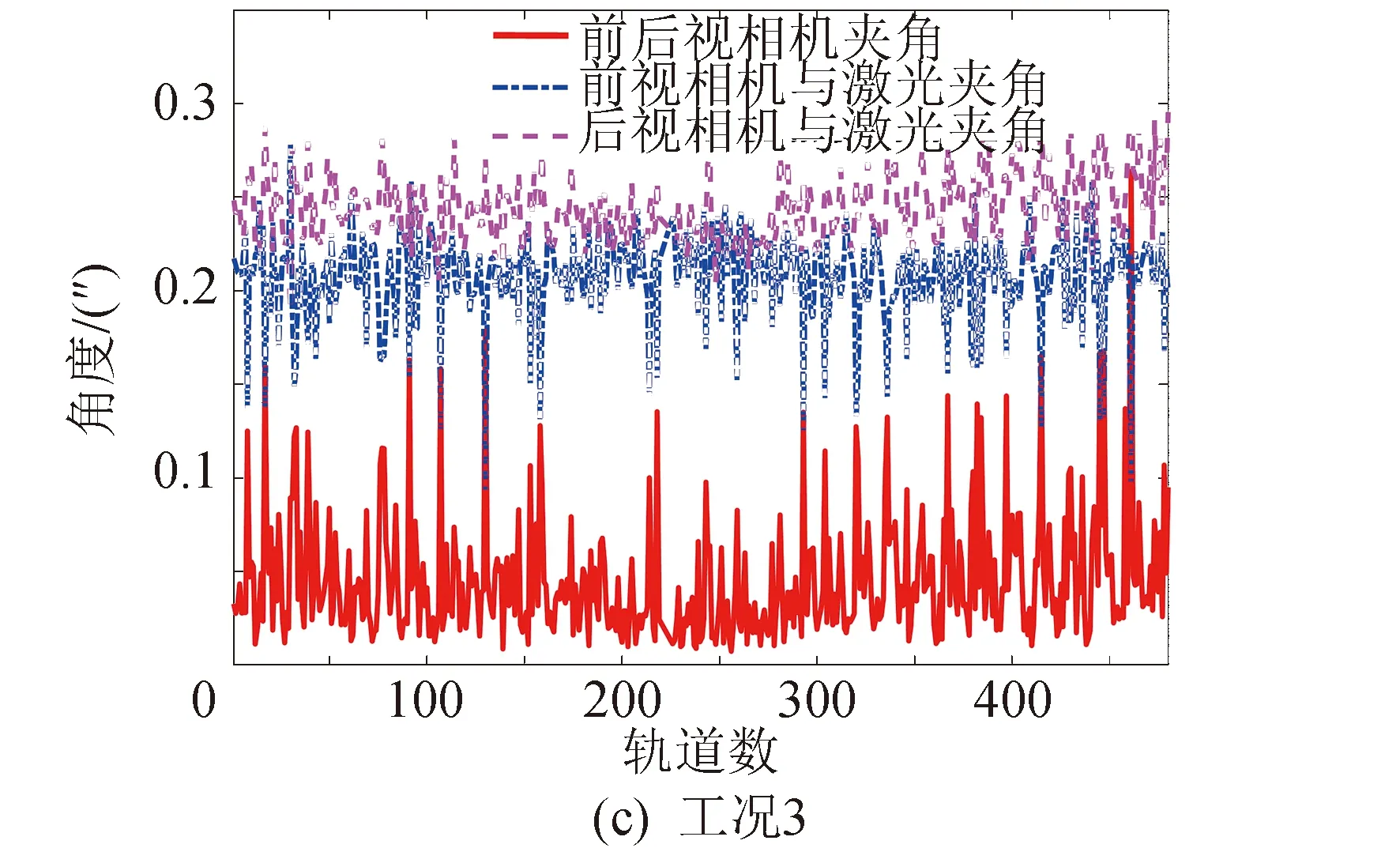
图4 成像期间载荷安装面法线夹角短期稳定性分析结果Fig.4 The short-term stability analysis resutls of the payloads mounting interface during imaging period
由表3可见,有95%的夹角稳定性的数值低于0.3″,即绝大部分的夹角稳定性优于0.3″,相当于所有数据最大值的75%。
4.3 长期稳定性指标分析
根据稳定性指标定义,长期稳定性定义为在一个标定期内对同一区域成像的稳定性。载荷标定周期一般根据卫星使用状态来确定。本文以1个月周期为示例,分析载荷安装面的长期稳定性,并对分析结果进行了统计分析。定义长期稳定性如下:

表2 1个月内成像期间短期稳定性统计分析结果
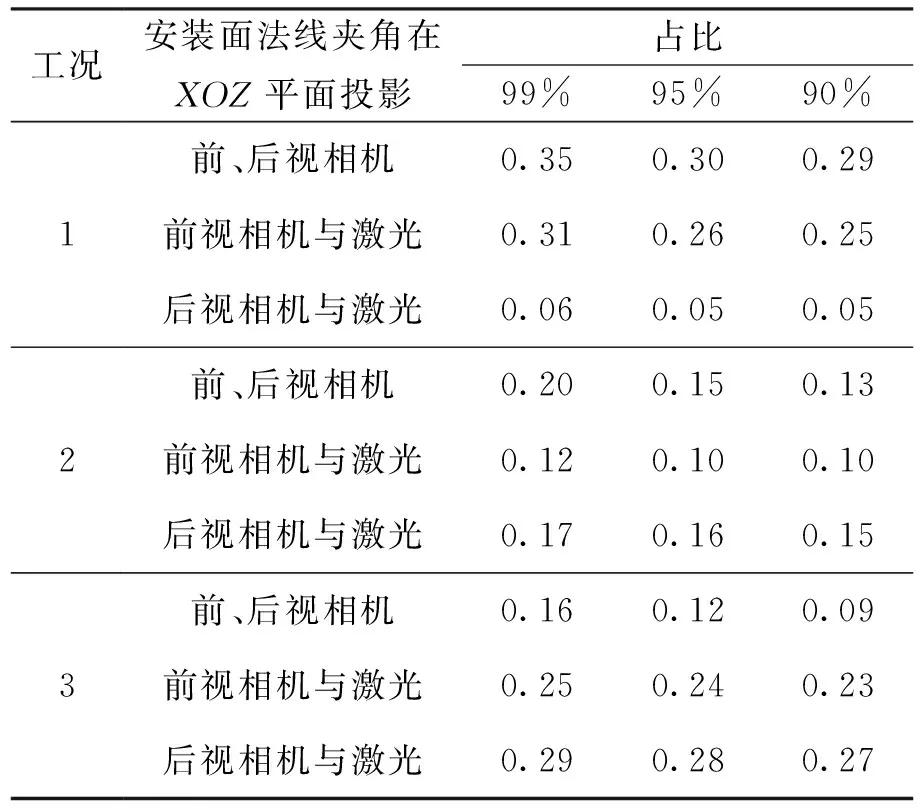
表3 短期稳定性幅值分布

(7)
根据式(7)计算得到长期稳定性,结果见表4和图5。结果表明,在1个月内,前、后视相机安装面法线夹角长期稳定性为0.37″,前视相机与激光安装面法线夹角长期稳定性为0.35″,后视相机与激光安装面法线夹角长期稳定性为0.16″,均远小于1.5″的指标要求。以上分析方法可以推广到任意载荷标定周期下的长期稳定性指标预示分析。
从图5可以看出,一轨内的不同时刻,长期尺寸稳定性是不同的,这也为选择与长期稳定性有关的成像时间提供了依据。

表4 1个月内成像期间载荷安装面长期稳定性
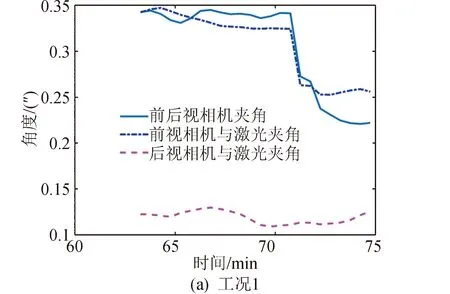
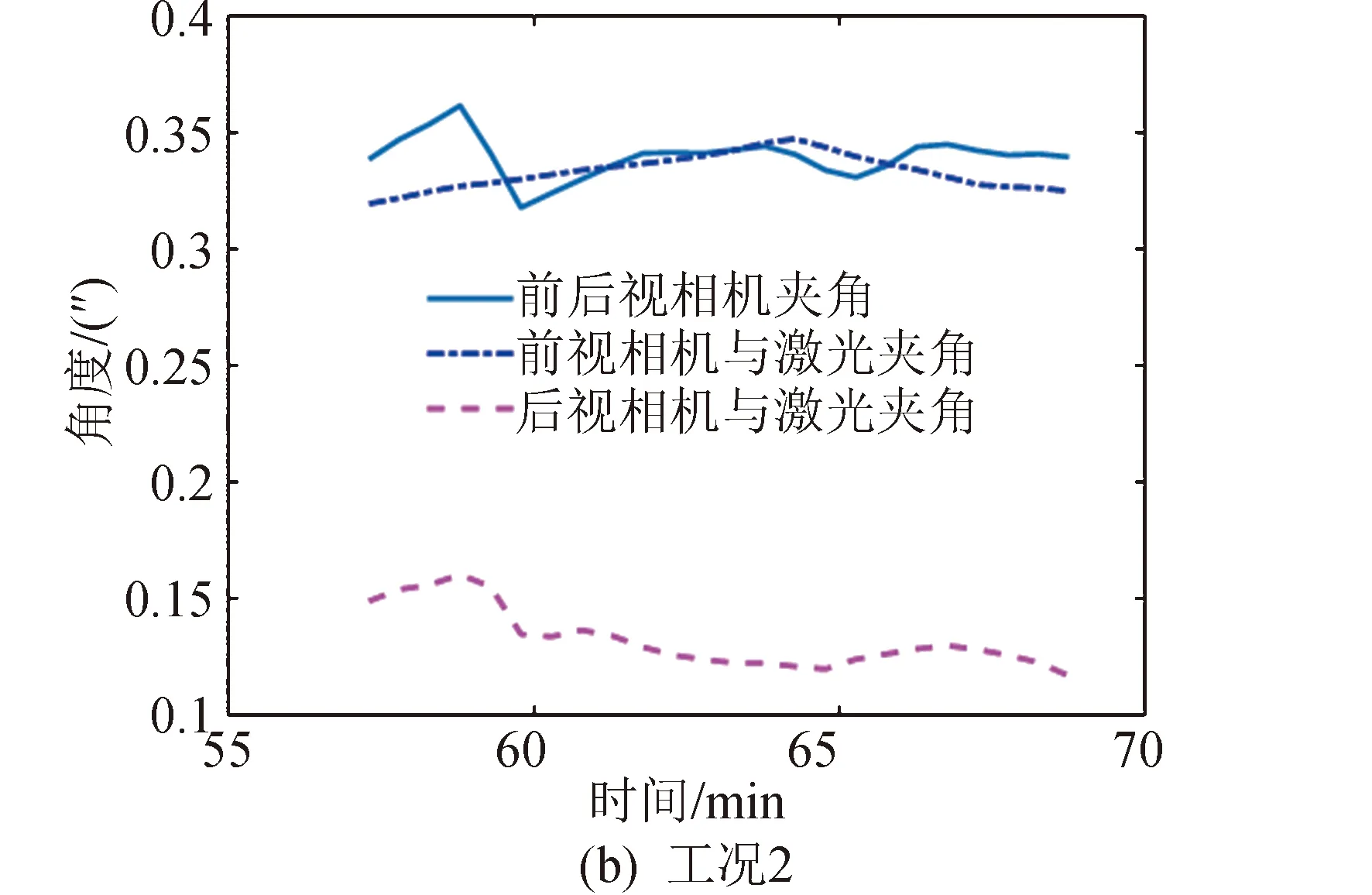
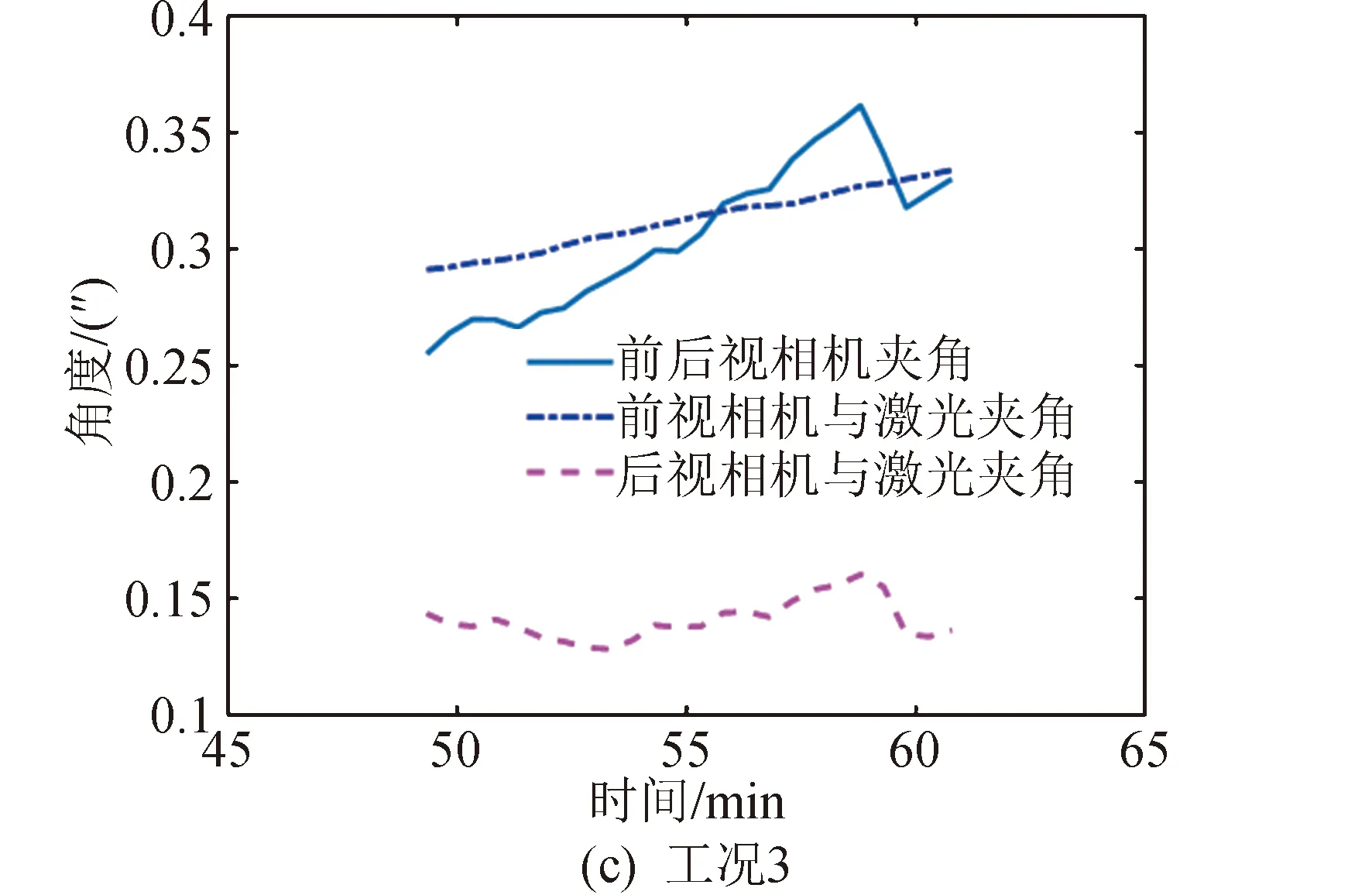
图5 1个月内工况1成像期间载荷安装面长期稳定性Fig.5 The long-term stability prediction resutls of the payloads mounting interface during imaging period
5 结束语
首次将分析得到的温度场与在轨遥测温度相结合,提出了整星在轨温度场的反演方法。该方法的最大特点是在温度遥测数据极端稀少的结构上,也能获得满足工程精度需要的反演温度场。基于上述方法,对高分七号卫星上3个有效载荷的夹角稳定性进行了计算。计算结果表明,结构由于热变形导致的有效载荷安装面法线夹角变化满足总体夹角稳定性指标要求。
本文是对航天器尺寸稳定性指标目前只能地面预示且很难在轨验证这一难题的一次突破。基于本文的工作,可以发现设计过程中不能观察到的现象,如夹角变化的非完美周期性。此外,还可以利用该方法计算各个夹角实际在轨时对航天器上各个部件的灵敏度,这为完善和改进设计提供了很好的依据。
为使本文提出的算法精度得到提高,需要考虑不同温度场反演区域之间的匹配以及反演精度的评价准则。
