基于强化学习的四旋翼无人机控制律设计
2021-03-16刘小雄张兴旺黄剑雄
梁 晨,刘小雄,张兴旺,黄剑雄
(西北工业大学 自动化学院, 西安 710072)
0 引言
近些年来随着科技的提升,旋翼无人机行业发展迅猛,应用场景越来越广阔,由于四旋翼具有可垂直起降、低成本和结构简单的特性,因此在公共安全、民用航拍、消防急救、农业植保以及军事领域具有十分广泛的用途。目前四旋翼无人机正在朝着易携带、多功能和更加安全高效的方向发展。
由于四旋翼是典型欠驱动非线性强耦合系统[1],四旋翼的速度和位置控制都依赖于姿态的控制,因此四旋翼的姿态控制一直是研究的热点之一[2-4]。然而四旋翼在飞行过程中容易受到环境的干扰,旋翼桨叶之间的气动干扰,存在电机快速旋转时产生的陀螺力矩以及旋翼质量分布不均等问题,这使得对四旋翼的精确建模尤为困难,从而导致依赖精确建模的传统控制算法[5]难以达到控制要求。
强化学习又称为增强学习,自从20世纪初便被提出来了,经过将近一个多世纪的发展,强化学习与心理学、智能控制、优化理论、计算智能、认知科学等学科有着密切的联系,是一个典型的多学科交叉领域。近些年来,得益于高速计算机、深度学习以及大数据技术的发展,强化学习得到了越来越广泛的关注,尤其是深度强化学习技术,被学术界认为是最有可能实现人工智能的算法,已经成为最受学者们关注的前沿技术之一。
2016年AlphaGo成功战胜了人类顶级棋手,使得深度强化学习得到了广泛的关注,之后的AlphaGo Zero,更是使得强化学习技术成为人工智能领域最热门的技术之一。强化学习技术不仅在博弈类游戏上取得了巨大成功,而且在控制领域也已有了新的突破,如在两轮车的控制[6]、倒立摆的控制[7]上均取得了较好的进展。本文提出一种将强化学习[8]与神经网络结合起来的端到端的控制方法,该方法只关心系统的输入输出,不关心系统内部过程,通过智能体与环境的不断交互,反馈奖惩信息来优化控制参数,从而避免了对四旋翼进行精确建模等问题。该方法输入为姿态角与姿态角速率,经过神经网络,计算出四旋翼的动作值函数,再通过贪婪策略对动作进行选取,得到四旋翼各个桨叶的拉力。通过强化学习的方法对神经网络进行训练,最终使得神经网络可以收敛。最终通过在强化学习算法工具包OpenAI Gym中建立四旋翼的模型,用本文设计的控制算法对该模型进行仿真控制,结果证明了该算法的有效性。
1 四旋翼动力学模型的建立
如图1所示,本文对“X”型结构的四旋翼进行动力学模型的建立。在惯性系中应用牛顿第二定律,可得四旋翼飞行器在合外力F作用下的线运动和合外力矩M作用下的角运动方程:
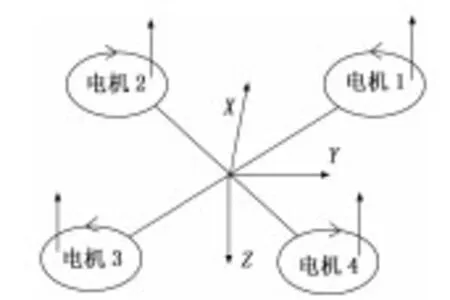
图1 四旋翼结构图

(1)
通过对桨叶动力学模型的分析和电机模型的建立,可以求得桨叶产生的力矩、旋翼惯性反扭力矩以及陀螺效应力矩。根据机体系与地面系的旋转关系可求得欧拉角速率与机体三轴角速率的关系:

(2)
当四旋翼姿态变化很小时,通过求解式(1),得到四旋翼飞行器的角运动方程:

(3)
其中:φ、θ、ψ为滚转角、俯仰角、偏航角;p、q、r为滚转角速率、俯仰角速率、偏航角速率;Ix、Iy、Iz分别为四旋翼飞行器绕x、y、z轴的转动惯量,Jr为每个桨叶的转动惯量;ΩG为陀螺力矩转速;
根据图1的四旋翼结构,定义UT、Uφ、Uθ、Uψ分别为四旋翼高度、滚转通道、俯仰通道以及偏航通道的控制输入,F1、F2、F3、F4分别为4个桨叶提供的拉力,则有:
(4)
其中:d表示旋翼转轴到x轴或y轴的距离;CM为反扭力矩系数,CT为升力系数。
2 基于强化学习的四旋翼姿态控制结构
图2为强化学习的基本图,强化学习是通过智能体与环境的不断交互来更新控制策略的。一开始,智能体随机选择一个动作A作用于环境,环境模型通过该动作使得整个系统达到一个新的状态,并且通过回报函数给智能体一个反馈。这样不断循环下去,智能体与环境持续地交互,从而产生更多的数据样本。智能体根据与环境交互而产生的数据样本来改变自身的动作选择策略。通过不断地试错,智能体最终会学到一个最优的策略。

图2 强化学习基本框图
从强化学习的基本原理中我们可以看出来,强化学习与监督学习和非监督学习有一些本质上的区别。如传统的监督学习中,数据样本是一些带有标签的静止训练集,只要样本数据之间的差异足够明显,就能够训练一个不错的模型。而强化学习则是一个连续决策的过程,在强化学习中,智能体没有直接的指导信息,而是通过环境反馈的立即回报来修正自身的策略,智能体需要不断地与环境进行交互从而实时地获取训练数据,通过这种试错的方式来获得最佳的策略。
本文采用基于值函数逼近的无模型强化学习算法Deep Q-Network[9]来对四旋翼姿态进行控制。DQN算法是在Q-Learning算法的基础上进行的改进,在Q-Learning算法中,维护一张表Q-Table它的每一列代表一个动作,每一行代表一个状态,这张表记录了每个状态下采取不同动作所获得的最大长期奖励期望,通过这张表就可以知道每一步的最佳动作是什么。但是在状态空间维度十分庞大甚至连续时,Q-Table不能存储下所有的状态,因此DeepMind对Q-Learning进行了改进,便得到了DQN算法,其改进主要体现在以下几个方面:
1)DQN利用卷积神经网络进行值函数的逼近;
2)DQN利用了经验回放训练强化学习的学习过程;
3)DQN中独立设置了目标网络来单独处理时间差分算法中的TD偏差。
DQN算法流程如图3所示,在DQN算法中,有几个比较重要的环节:环境、当前值网络与目标值网络、动作库、经验池以及回报函数。环境模型在上一节中已经建立,其余的将在本节进行建立。

图3 DQN算法流程
1)动作库:本文中动作库是俯仰、滚转、偏航三通道的控制量Uφ、Uθ、Uψ。
2)值函数神经网络:在DQN中,存在两个结构完全相同的逼近值函数的神经网络:一个是当前值函数神经网络,另一个是目标值函数神经网络。当前值函数与目标值函数的差作为部分依据修正神经网络的参数,当前值函数神经网络每一步都更新,而目标值函数神经网络每隔一定的步数更新。本文采用三层BP神经网络作为值函数神经网络,输入维度为2,对应单个通道的角度与角速率,输出维度对应单个通道的动作库维度。
网络参数的更新如下所示:
Q(s,a;θ)]·▽Q(s,a;θ)
(5)
其中:θ为网络参数;α为学习速率;r为立即回报;γ为折扣因子;s和a分别为状态与动作。
3)经验池:由于强化学习是建立在马尔科夫决策过程的基础上的,因此通过强化学习得到的样本数据之间存在着相关性,而神经网络的前提是样本之间独立同分布。基于此,建立一个经验池,将通过强化学习得到的数据存在经验池中,训练时从经验池中随机均匀采取一些样本进行训练,以此来打破数据样本之间存在的相关性。
4)回报函数:本文研究内容是四旋翼的姿态控制,以滚转角φ单通道为例,设计回报函数如下:
(6)
当角度偏差或角速度比较大时,对智能体惩罚比较大,反之则惩罚较小。强化学习会对智能体朝着使得累积回报最大的方向进行训练。
3 四旋翼姿态控制律设计
基于以上分析,设计基于无模型强化学习算法DQN的四旋翼控制律,模型参数如表1所示。

表1 模型参数
具体设计如下:
由于三通道的控制律结构一致,因此以下仅以滚转通道为例进行介绍。依据第二章四旋翼姿态控制结构,需要建立两个结构相同但参数不同的神经网络,即目标网络和现实网络,定义目标网络的参数为θ-,现实网络的参数为θ。本文采用三层BP神经网络对值函数进行拟合,神经网络输入层有两个神经元,分别为俯仰角偏差与俯仰角速率;隐藏层有10个神经元;输出层有20个神经元,对应俯仰通道的动作值函数。
设置经验池大小为5 000,经验池中每一个样本存储智能体的上一步状态st、当前状态st+1、环境给予的立即回报r以及在当前状态下所选取的动作a,当样本数据大于5 000时,可以认为前面的数据已经不具备参考价值,删除掉最早的数据。

图4 经验池
规定每次训练时从经验池中随机均匀抽取50条样本进行训练。因为训练时系统使用ε贪婪策略进行动作的选取,所以为使系统一开始具备较强的探索能力,尽最大可能探索到范围以内的所有状态,不至于收敛到局部最优,实验中将ε贪婪值初始化为0,每隔1 000步,贪婪值增加0.01,最大增加到0.95。
在实验中,给定初始角度偏差为5°,同时初始化角速度为0°/s,开始训练智能体。训练采取回合制,为防止智能体收敛到局部最优,为每一个回合设定最大仿真步数,当角度偏差超过设定范围或者本回合步数超过最大步数时,本回合结束,开始下一回合训练。实验中,对仿真回合不做限制,但是每一个回合将输出损失与参数模型,实验中可以随时终止训练并将模型导出。
综上所述,以贪婪策略作为滚转通道控制量的选取策略,即滚转通道控制量取值为值函数中值最大的元素所对应的动作,即:
(7)
4 仿真结果与分析
根据第3小节所描述的实验方法进行实验,仿真步骤如下所示:
1)初始化一些必要的参数,如动作库、贪婪值、初始角度偏差、经验池大小、每次训练所采的样本数等;
2)开始训练,训练时动作的选取采用ε贪婪策略。每回合训练时输出损失与参数模型,当损失达到一定要求之后,停止训练,保存参数模型。对俯仰、滚转、偏航通道分别进行如上所示的训练并保存好参数模型;
3)将参数模型输入到最终的仿真模型中,并通过式(4)反解出每个电机的拉力,从而实现对四旋翼的姿态控制。
仿真电脑CPU为Intel i5-7500,内存8.00 GB,在ubuntu16.04系统下,采用OpenAI Gym工具包进行仿真,训练效果如图5所示。

图5 损失函数曲线
从损失函数曲线中可以看出,在强化学习的训练下,神经网络基本上从4 000步开始就已经收敛了,而到10 000步左右时出现小幅的波动,这是因为贪婪策略取值最大为0.95,系统依然有5%的概率随机选取动作,这会导致目标网络与现实网络之间的偏差增大,进而导致损失函数的增加。实验中,选取了第4 000步时的模型参数作为最终的模型参数。

图6 初始值为正时Δφ的变化
将训练好的模型输入系统控制结构中,并对角度观测量加入[0.1,0.1]上的随机噪声,初始化φ为5°,设置期望值为0度进行仿真实验。如图6所示,系统基本上能够在1 s以内达到控制目标,并且稳定在目标值左右。
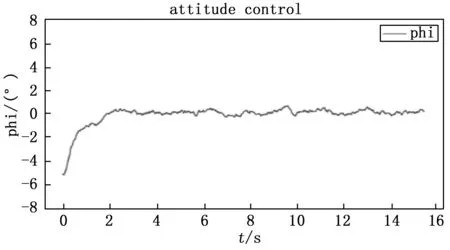
图7 初始值为负时Δφ的变化
将Δφ的初始值为-5时训练得到的模型参数,重新输入到飞机模型中,得到曲线如图7所示。
由以上分析,将训练好的网络模型输入到飞机模型中,控制器输入为期望角度值,将当前角度值与期望角度值做差,当角度偏差为正时通过第一个网络模型进行控制,当角度偏差为负时通过第二个网络模型进行控制。
图8为φ的控制效果图,将系统初始角度与期望角度分别设置为5°和0°,并在第5 s、10 s、15 s时分别改变系统的期望角度,可以看到,系统基本可以跟上控制指令。
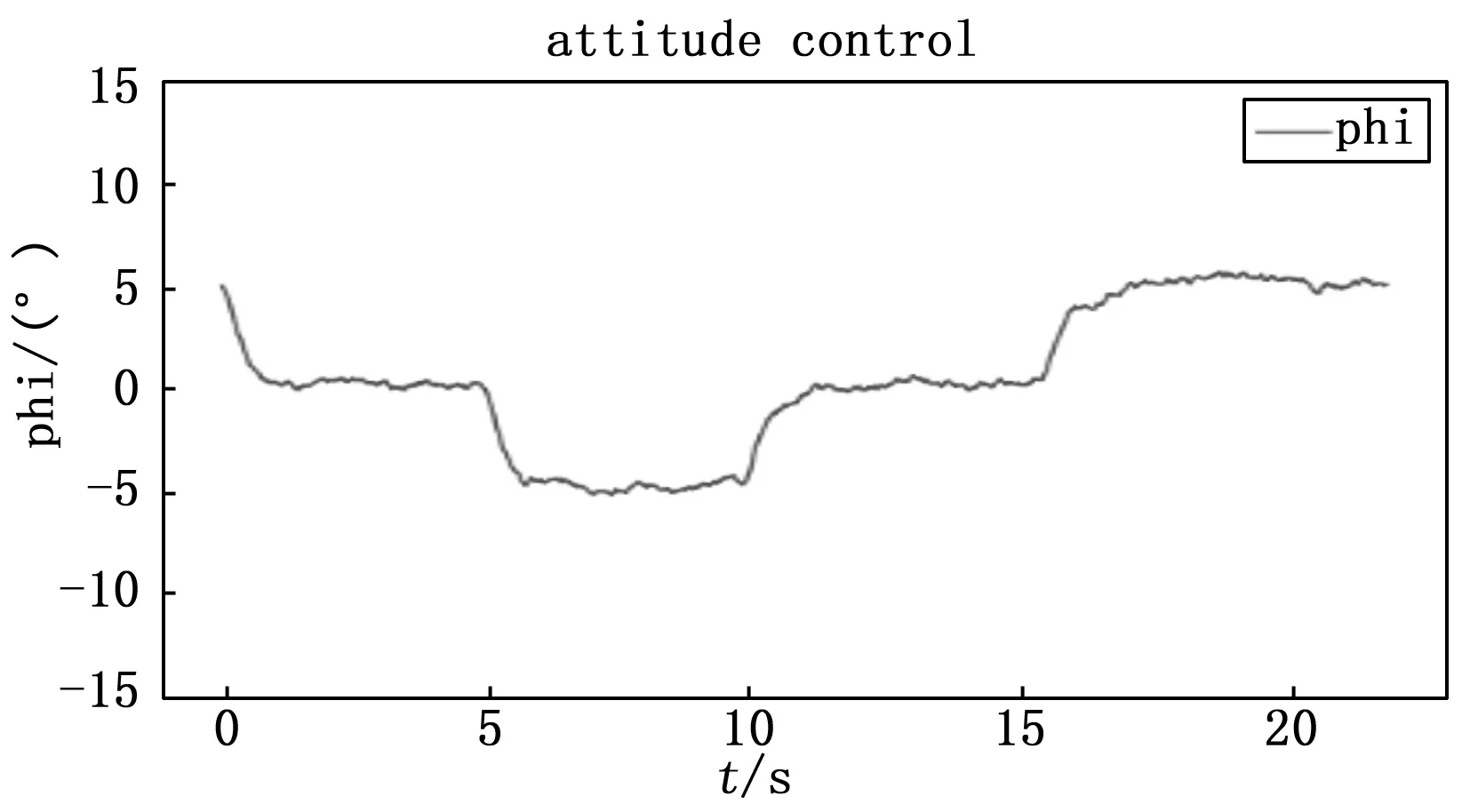
图8 φ的控制效果图
同理,俯仰角和偏航角的控制结构与滚转角一致,俯仰通道与偏航通道的控制效果如下:
图9、图10分别为俯仰角和偏航角的控制效果图。将俯仰角的初始值和期望值分别设置为-5°和0°,然后在5 s、10 s、15 s时分别改变俯仰角期望值为5°、0°和-5°,得到曲线如图9(c)所示。同理将偏航角的初始值与期望值分别设置为10°和0°,然后在5 s、10 s、15 s时分别改变偏航角的值为10°、0°和-10°,得到曲线如图10(c)所示。
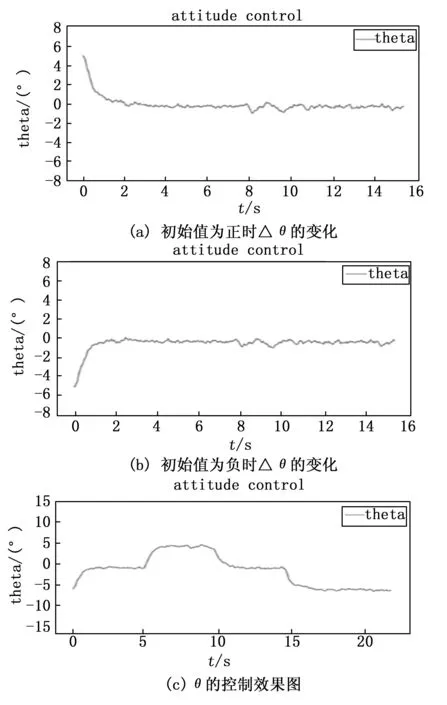
图9 俯仰角的控制效果图

图10 偏航角的控制效果图
综合以上曲线可以看出,在单独控制一个通道时,基于DQN的控制律基本可以快速准确地跟踪上指令信号的改变。接着将三通道的控制量通过下式求出各桨叶所提供的拉力,从而达到控制四旋翼飞行器的目的。
(8)
其中:Ac为系数矩阵。
图11为将各通道控制量经过控制分配之后得到的四旋翼姿态控制效果图。

图11 四旋翼姿态角控制效果
实验中,将四旋翼三轴姿态角均初始化为0°,角度观测量均加入[-0.1,0.1]上的随机噪声,通过在不同时刻给定四旋翼不同的指令信号,使得四旋翼达到不同姿态,最终效果如图11所示。
从图11中可以看出,控制器基本上可以使得四旋翼的姿态跟上指令信号,但同时伴随有一定的震荡,还会有一定的误差。这是因为DQN中,动作空间并不是连续的,在一些状态下,智能体所需要选择的最优动作并不存在于动作空间中,这时智能体只能选择动作空间中最接近最优动作的动作,这就造成了四旋翼姿态必然会伴随有一定的震荡和误差。因此想要减小震荡并消除误差,这能增加动作空间的维度,将动作空间设置的更加稠密,这样智能体选择的动作就会更加接近最优值。
5 结束语
本文针对“X”型结构的四旋翼非线性运动模型,提出基于无模型强化学习算法DQN的四旋翼姿态控制律设计[10]。首先对俯仰角、滚转角以及偏航角分别进行控制律设计,当三通道控制律达到控制要求之后,通过控制分配求出4个桨叶的拉力,进而达到控制四旋翼姿态的目的。实验结果表明基于无模型强化学习的控制律能够在不知道被控对象模型的情况下,控制四旋翼实时跟踪上参考指令的变化。
